Direct extraction of signal and noise correlations from two-photon calcium imaging of ensemble neuronal activity
Abstract
Neuronal activity correlations are key to understanding how populations of neurons collectively encode information. While two-photon calcium imaging has created a unique opportunity to record the activity of large populations of neurons, existing methods for inferring correlations from these data face several challenges. First, the observations of spiking activity produced by two-photon imaging are temporally blurred and noisy. Secondly, even if the spiking data were perfectly recovered via deconvolution, inferring network-level features from binary spiking data is a challenging task due to the non-linear relation of neuronal spiking to endogenous and exogenous inputs. In this work, we propose a methodology to explicitly model and directly estimate signal and noise correlations from two-photon fluorescence observations, without requiring intermediate spike deconvolution. We provide theoretical guarantees on the performance of the proposed estimator and demonstrate its utility through applications to simulated and experimentally recorded data from the mouse auditory cortex.
Introduction
Neuronal activity correlations are essential in understanding how populations of neurons encode information. Correlations provide insights into the functional architecture and computations carried out by neuronal networks (Abbott and Dayan, 1999; Averbeck et al., 2006; Cohen and Kohn, 2011; Hansen et al., 2012; Kohn et al., 2016; Kohn and Smith, 2005; Lyamzin et al., 2015; Montijn et al., 2014; Smith and Sommer, 2013; Sompolinsky et al., 2001; Yatsenko et al., 2015). Neuronal activity correlations are often categorized in two groups: signal correlations and noise correlations (Cohen and Kohn, 2011; Cohen and Maunsell, 2009; Gawne and Richmond, 1993; Josić et al., 2009; Lyamzin et al., 2015; Vinci et al., 2016). Given two neurons, signal correlation quantifies the similarity of neural responses that are time-locked to a repeated stimulus across trials, whereas noise correlation quantifies the stimulus-independent trial-to-trial variability shared by neural responses that are believed to arise from common latent inputs.
Two-photon calcium imaging has become increasingly popular in recent years to record in vivo neural activity simultaneously from hundreds of neurons (Ahrens et al., 2013; Romano et al., 2017; Stosiek et al., 2003; Svoboda and Yasuda, 2006). This technology takes advantage of intracellular calcium flux mostly arising from spiking activity and captures calcium signaling in neurons in living animals using fluorescence microscopy. The observed fluorescence traces of calcium concentrations, however, are indirectly related to neuronal spiking activity. Extracting spiking activity from fluorescence traces is a challenging signal deconvolution problem and has been the focus of active research (Deneux et al., 2016; Friedrich et al., 2017; Grewe et al., 2010; Jewell et al., 2020; Jewell and Witten, 2018; Kazemipour et al., 2018; Pachitariu et al., 2018; Pnevmatikakis et al., 2016; Stringer and Pachitariu, 2019; Theis et al., 2016; Vogelstein et al., 2009; Vogelstein et al., 2010).
The most commonly used approach to infer signal and noise correlations from two-photon data is to directly apply the classical definitions of correlations for firing rates (Lyamzin et al., 2015), to fluorescence traces (Fallani et al., 2015; Francis et al., 2018; Rothschild et al., 2010; Winkowski and Kanold, 2013). However, it is well known that fluorescence observations are noisy and blurred surrogates of spiking activity, because of dependence on observation noise, calcium dynamics and the temporal properties of calcium indicators. Due to temporal blurring, the resulting signal and noise correlation estimates are highly biased. An alternative approach is to carry out the inference in a two-stage fashion: first, infer spikes using a deconvolution technique, and then compute firing rates and evaluate the correlations (Kerlin et al., 2019; Najafi et al., 2020; Ramesh et al., 2018; Soudry et al., 2015; Yatsenko et al., 2015). These two-stage estimates are highly sensitive to the accuracy of spike deconvolution, and require high temporal resolution and signal-to-noise ratios (Lütcke et al., 2013; Pachitariu et al., 2018). Furthermore, these deconvolution techniques are biased toward obtaining accurate first-order statistics (i.e. spike timings) via spatiotemporal priors, which may be detrimental to recovering second-order statistics (i.e. correlations). Finally, both approaches also undermine the non-linear dynamics of spiking activity as governed by stimuli, past activity and other latent processes (Truccolo et al., 2005). There are a few existing studies that aim at improving estimation of neuronal correlations, but they either do not consider signal correlations (Rupasinghe and Babadi, 2020; Yatsenko et al., 2015), or aim at estimating surrogates of correlations from spikes such as the connectivity/coupling matrix (Aitchison et al., 2017; Mishchenko et al., 2011; Soudry et al., 2015; Keeley et al., 2020).
Here, we propose a methodology to directly estimate both signal and noise correlations from two-photon imaging observations, without requiring an intermediate step of spike deconvolution. We pose the problem under the commonly used experimental paradigm in which neuronal activity is recorded during trials of a repeated stimulus. We avoid the need to perform spike deconvolution by integrating techniques from point processes and state-space modeling that explicitly relate the signal and noise correlations to the observed fluorescence traces in a multi-tier model. Thus, we cast signal and noise correlations within a parameter estimation setting. To solve the resulting estimation problem in an efficient fashion, we develop a solution method based on variational inference (Jordan et al., 1999; Blei et al., 2017), by combining techniques from Pólya-Gamma augmentation (Polson et al., 2013) and compressible state-space estimation (Rauch et al., 1965; Kazemipour et al., 2018; Ba et al., 2014). We also provide theoretical guarantees on the bias and variance performance of the resulting estimator.
We demonstrate the utility of our proposed estimation framework through application to simulated and real data from the mouse auditory cortex during presentations of tones and acoustic noise. In application to repeated trials under spontaneous and stimulus-driven conditions within the same experiment, our method reliably provides noise correlation structures that are invariant across the two conditions. In addition, our joint analysis of signal and noise correlations corroborates existing hypotheses regarding the distinction between their structures (Keeley et al., 2020; Rumyantsev et al., 2020; Bartolo et al., 2020). Moreover, while application of our proposed method to spatial analysis of signal and noise correlations in the mouse auditory cortex is consistent with existing work (Winkowski and Kanold, 2013), it reveals novel and distinct spatial trends in the correlation structure of layers 2/3 and 4. In summary, our method improves on existing work by: (1) explicitly modeling the fluorescence observation process and the non-linearities involved in spiking activity, as governed by both the stimulus and latent processes, through a multi-tier Bayesian forward model, (2) joint estimation of signal and noise correlations directly from two-photon fluorescence observations through an efficient iterative procedure, without requiring intermediate spike deconvolution, (3) providing theoretical guarantees on the performance of the proposed estimator, and (4) gaining access to closed-form posterior approximations, with low-complexity and iterative update rules and minimal dependence on training data. Our proposed method can thus be used as a robust and scalable alternative to existing approaches for extracting signal and noise correlations from two-photon imaging data.
Results
In this section, we first demonstrate the utility of our proposed estimation framework through simulation studies as well as applications on experimentally recorded data from the mouse auditory cortex. Then, we present theoretical performance bounds on the proposed estimator. Before presenting the results, we will give an overview of the proposed signal and noise correlation inference framework, and outline our contributions and their relationship to existing work. For the ease of reproducibility, we have archived a MATLAB implementation of our proposed method in GitHub (Rupasinghe, 2020) and have deposited the data used in this work in the Digital Repository at the University of Maryland (Rupasinghe et al., 2021).
Signal and noise correlations
We consider a canonical experimental setting in which the same external stimulus, denoted by , is repeatedly presented across independent trials and the spiking activity of a population of neurons are indirectly measured using two-photon calcium fluorescence imaging. Figure 1 (forward arrow) shows the generative model that is used to quantify this procedure. The fluorescence observation in the trial from the neuron at time frame , denoted by , is a noisy surrogate of the intracellular calcium concentrations. The calcium concentrations in turn are temporally blurred surrogates of the underlying spiking activity , as shown in Figure 1.
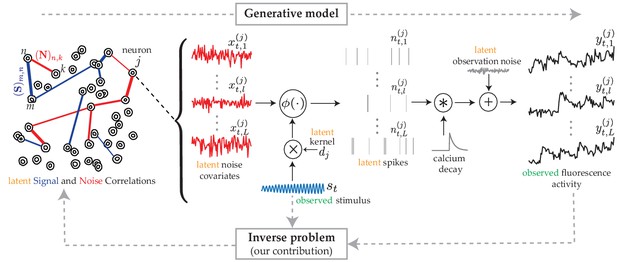
The proposed generative model and inverse problem.
Observed (green) and latent (orange) variables pertinent to the neuron are indicated, according to the proposed model for estimating the signal (blue) and noise (red) correlations from two-photon calcium fluorescence observations. Calcium fluorescence traces of trials are observed, in which the repeated external stimulus is known. The underlying spiking activity , trial-to-trial variability and other intrinsic/extrinsic neural covariates that are not time-locked with the external stimulus , and the stimulus kernel are latent. Our main contribution is to solve the inverse problem: recovering the underlying latent signal and noise correlations directly from the fluorescence observations, without requiring intermediate spike deconvolution.
In modeling the spiking activity, we consider two main contributions: (1) the common known stimulus affects the activity of the neuron via an unknown kernel , akin to the receptive field; (2) the trial-to-trial variability and other intrinsic/extrinsic neural covariates that are not time-locked to the stimulus are captured by a trial-dependent latent process . Then, we use a Generalized Linear Model to link these underlying neural covariates to spiking activity (Truccolo et al., 2005). More specifically, we model spiking activity as a Bernoulli process:
where is a mapping function, which could in general be non-linear.
The signal correlations aim to measure the correlations in the temporal response that are time-locked to the repeated stimulus, . On the other hand, noise correlations in our setting quantify connectivity arising from covariates that are unrelated to the stimulus, including the trial-to-trial variability (Keeley et al., 2020). Based on the foregoing model, we propose to formulate the signal and noise covariance between the neuron and neuron as:
where is the empirical covariance function defined for two vector time series and as , for a total observation duration of time frames.
Our main contribution is to provide an efficient solution for the so-called inverse problem: direct estimation of and from the fluorescence observations, without requiring intermediate spike deconvolution (Figure 1, backward arrow). The signal and noise correlation matrices, denoted by and , can then be obtained by standard normalization of and :
We note that when spiking activity is directly observed using electrophysiology recordings, the conventional signal and noise covariances of spiking activity between the and neuron are defined as (Lyamzin et al., 2015):
which after standard normalization in Equation 2 give the conventional signal and noise correlations. While at first glance, our definitions of signal and noise covariances in Equation 1 seem to be a far departure from the conventional ones in Equation 3, we show that the conventional notions of correlation indeed approximate the same quantities as in our definitions:
under asymptotic conditions (i.e. and sufficiently large). We prove this assertion of asymptotic equivalence in Appendix 1, which highlights another facet of our contributions: our proposed estimators are designed to robustly operate in the regime of finite (and typically small) and , aiming for the very same quantities that the conventional estimators could only recover accurately under ideal asymptotic conditions.
Existing methods used for performance comparison
In order to compare the performance of our proposed method with existing work, we consider three widely available methods for extracting neuronal correlations. In simulation studies, we additionally benchmark these estimates with respect to the known ground truth. The existing methods considered are the following:
Pearson correlations from the two-photon data
In this method, fluorescence observations are assumed to be the direct measurements of spiking activity, and thus empirical Pearson correlations of the two-photon data are used to compute the signal and noise correlations (Rothschild et al., 2010; Winkowski and Kanold, 2013; Francis et al., 2018; Bowen et al., 2020). Explicitly, these estimates are obtained by simply replacing in Equation 3 by , without performing spike deconvolution.
Two-stage Pearson estimation
Unlike the previous method, in this case spikes are first inferred using a deconvolution technique. Then, following temporal smoothing via a narrow Gaussian kernel the Pearson correlations are computed using the conventional definitions of Equation 3. For spike deconvolution, we primarily used the FCSS algorithm (Kazemipour et al., 2018). In order to also demonstrate the sensitivity of these estimates to the deconvolution technique that is used, we provide a comparison with the f-oopsi deconvolution algorithm (Pnevmatikakis et al., 2016) in Figure 2—figure supplement 1.
Two-stage GPFA estimation
Similar to the previous method, spikes are first inferred using a deconvolution technique. Then, a latent variable model called Gaussian Process Factor Analysis (GPFA) (Yu et al., 2009) is applied to the inferred spikes in order to estimate the latent covariates and receptive fields. Based on those estimates, the signal and residual noise correlations are derived through a formulation similar to Equation 1 and Equation 2 (Ecker et al., 2014).
Simulation study 1: neuronal ensemble driven by external stimulus
We simulated calcium fluorescence observations according to the proposed generative model given in Proposed forward model, from an ensemble of neurons for a duration of time frames. We considered repeated trials driven by the same external stimulus, which we modeled by an autoregressive process (see Guidelines for model parameter settings for details). Figure 2 shows the corresponding estimation results.
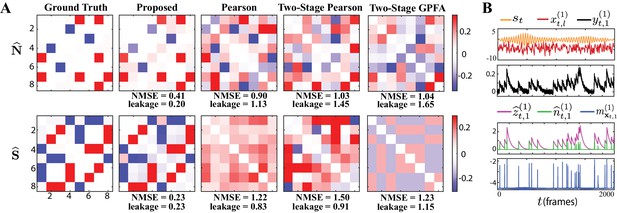
Results of simulation study 1.
(A) Estimated noise and signal correlation matrices from different methods. Rows from left to right: ground truth, proposed method, Pearson correlations from two-photon recordings, two-stage Pearson estimates and two-stage GPFA estimates. The normalized mean squared error (NMSE) of each estimate with respect to the ground truth and the leakage effect quantified by the ratio between out-of-network and in-network power (leakage) are indicated below each panel. (B) Simulated external stimulus (orange), latent trial-dependent process (red), fluorescence observations (black), estimated calcium concentrations (purple), putative spikes (green), and estimated mean of the latent state (blue) by the proposed method, for the first trial of neuron 1.
The first column of Figure 2A shows the ground truth noise (top) and signal (bottom) correlations (diagonal elements are all equal to one and omitted for visual convenience). The second column shows estimates of the noise and signal correlations using our proposed method, which closely match the ground truth. The third, fourth and fifth columns, respectively, show the results of the Pearson correlations from the two-photon data, two-stage Pearson, and two-stage GPFA estimation methods. Through a qualitative visual inspection, it is evident that these methods incur high false alarms and mis-detections of the ground truth correlations.
To quantify these comparisons, the normalized mean square error (NMSE) of different estimates with respect to the ground truth are shown below each of the subplots (Figure 2A). Our proposed method achieves the lowest NMSE compared to the others. Furthermore, we observed a significant mixing between signal and noise correlations in these other estimates. To quantify this leakage effect, we first classified each of the correlation entries as in-network or out-of-network, based on being non-zero or zero in the ground truth, respectively (see Performance evaluation). We then computed the ratio between the power of out-of-network components and the power of in-network components as a measure of leakage. The leakage ratios are also reported in Figure 2A. The leakage of our proposed estimates is the lowest of all four techniques, in estimating both the signal and noise correlations. In order to further probe the performance of our proposed method, the simulated external stimulus st, latent trial-dependent process , simulated observations , estimated calcium concentration , the putative spikes , and the estimated mean of the latent state , for the first trial of the first neuron are shown in Figure 2B. These results demonstrate the ability of the proposed estimation framework in accurately identifying the latent processes, which in turn leads to an accurate estimation of the signal and noise correlations as shown in Figure 2B.
The main sources of the observed performance gap between our proposed method and the existing ones are the bias incurred by treating the fluorescence traces as spikes, low spiking rates, non-linearity of spike generation with respect to intrinsic and external covariates, and sensitivity to spike deconvolution. For the latter, we demonstrated the sensitivity of the two-stage Pearson estimates to the choice of the deconvolution technique in Figure 2—figure supplement 1. Furthermore, in order to isolate the effect of said non-linearities on the estimation performance, we applied the two-stage methods to ground truth spikes in Figure 2—figure supplement 2. Our analysis showed that both two-stage estimates incur significant estimation errors even if the spikes were recovered perfectly, mainly due to the limited number of trials ( here). In accordance with our theoretical analysis of the asymptotic behavior of the conventional signal and noise correlation estimates given in Appendix 1, we also showed in Figure 2—figure supplement 2 that the performance of the two-stage Pearson estimates based on ground truth spikes, but using trials, dramatically improves. Our proposed method, however, was capable of producing reliable estimates with the number of trials as low as , which is typical in two-photon imaging experiments.
Analysis of robustness with respect to modeling assumptions
While the preceding results are quite favorable to our proposed method, the underlying generative models were the same as those used to estimate signal and noise correlations, which is in contrast to conventional real data validation with known ground truth. Access to ground truth correlations in two-photon imaging experimental settings, however, is quite challenging. In order to further probe the robustness of our proposed method in the absence of ground truth data, we utilized surrogate data that parallel the setting of Figure 2, but deviate from our modeling assumptions.
Robustness to stimulus integration model mismatch. First, we considered surrogate data generated with a non-linear stimulus integration model by replacing the linear receptive field component with , where and are akin to quadratic receptive field components. We assumed a linear stimulus integration model in our estimation framework (i.e., ). Figure 2—figure supplement 3 shows the resulting correlation estimates. While the performance of our proposed signal correlation estimates degrade under this setting as compared to Figure 2, our proposed estimates still outperform existing methods. In addition, the model mismatch in the stimulus integration component does not affect the accuracy of noise correlation estimation in our method.
Robustness to calcium decay model mismatch. Next, we tested our proposed estimation framework on data simulated with a different calcium decay model. Specifically, we simulated data with second-order autoregressive calcium dynamics, and at a lower signal-to-noise ratio (SNR) compared to the setting of Figure 2, and used our inference framework which assumes first order calcium dynamics for estimation. Figure 2—figure supplement 4 shows the corresponding noise and signal correlations estimated by the proposed method under these conditions. Even though the performance slightly degrades (in terms of NMSE and leakage ratio), our method is able to recover the underlying correlations faithfully under this setting.
Robustness to SNR level and firing rate. Next, we compared the performance of Pearson and Two-Stage Pearson methods with our proposed method under varying SNR levels and average firing rates, as shown in Figure 2—figure supplement 5. While the performance of all methods degrades at low SNR levels or firing rates (SNR < 10 dB, firing rate < 0.5 Hz), our proposed method outperforms the existing methods for a wide range of SNR and firing rate values. To quantify this comparison, we have also indicated the mean and standard deviation of the relative performance gain of our proposed estimates across SNR levels and firing rates as insets in Figure 2—figure supplement 5.
Robustness to observation noise model mismatch. Finally, we repeated the foregoing comparisons under varying SNR levels and firing rates, only now we included an additional observation noise model mismatch. Similar to the treatment in Deneux et al., 2016, we considered two temporally correlated observation noise models: white noise with a low frequency drift (Figure 2—figure supplement 6, top panels) and pink noise (Figure 2—figure supplement 6, bottom panels). In accordance with the results in Figure 2—figure supplement 5, our proposed method outperforms the existing ones for a wide range of SNR and firing rate values and under both observation noise model mismatch conditions. From Figure 2—figure supplement 6C and F, it can be observed that the ground truth spikes are favorably recovered as a byproduct of our method, even though the estimated calcium concentrations are contaminated by the temporally correlated fluctuations in observation noise. This in turn results in accurate signal and noise correlation estimates.
Simulation study 2: spontaneous activity
Next, we present the results of a simulation study in the absence of external stimuli (i.e. ), pertaining to the spontaneous activity condition. It is noteworthy that the proposed method can readily be applied to estimate noise correlations during spontaneous activity, by simply setting the external stimulus and the receptive field to zero in the update rules (see Proposed forward model for details). We simulated the ensemble spiking activity based on a Poisson process (Smith and Brown, 2003) using a discrete time-rescaling procedure (Brown et al., 2002; Smith and Brown, 2003), so that the data are generated using a different model than that used in our inference framework (i.e. Bernoulli process with a logistic link as outlined in Proposed forward model). As such, we eliminated potential performance biases in favor of our proposed method by introducing the aforementioned model mismatch. We simulated independent trials of spontaneous activity of neurons, observed for a time duration of time frames. The number of neurons in this study is notably larger than that used in the previous one, to examine the scalability of our proposed approach with respect to the ensemble size.
Figure 3 shows the comparison of the noise correlation matrices estimated by our proposed method, Pearson correlations from two-photon recordings, two-stage Pearson, and two-stage GPFA estimates, with respect to the ground truth. The Pearson and the two-stage estimates are highly variable and result in excessive false detections. Our proposed estimate, however, closely follows the ground truth, which is also reflected by the comparatively lower NMSE and leakage ratios, in spite of the mismatch between the models used for data generation and inference. In addition, our proposed method exhibits favorable scaling with respect to the ensemble size, thanks to the underlying low-complexity variational updates (see Low-complexity parameter updates for details).
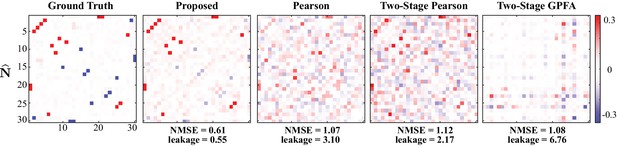
Results of simulation study 2.
Estimated noise correlation matrices using different methods based from spontaneous activity data. Rows from left to right: ground truth, proposed method, Pearson correlations from two-photon recordings, two-stage Pearson and two-stage GPFA estimates. The normalized mean squared error (NMSE) of each estimate with respect to the ground truth and the ratio between out-of-network power and in-network power (leakage) are shown below each panel.
Real data study 1: mouse auditory cortex under random tone presentation
We next applied our proposed method to experimentally recorded two-photon observations from the mouse primary auditory cortex (A1). The dataset consisted of recordings from 371 excitatory neurons in layer 2/3 A1, from which we selected responsive neurons (i.e. neurons that exhibited at least one spiking event in at least half of the trials considered; see Guidelines for model parameter settings). A random sequence of four tones was presented to the mouse, with the same sequence being repeated for trials. Each trial consisted of time frames, and each tone was 2 s long followed by a 4 s silent period (see Experimental procedures for details). We considered an integration window of frames for stimulus encoding (see Guidelines for model parameter settings for details). The comparison of the noise and signal correlation estimates obtained by our proposed method, Pearson correlations from two-photon recordings, two-stage Pearson and two-stage GPFA methods is shown in Figure 4A. The spatial map of the 16 neurons considered in the analysis in the field of view is shown in Figure 4B. Figure 4C shows the stimulus tone sequence st , two-photon observations , estimated calcium concentration , putative spikes and the estimated mean of the latent state , for the first trial of the first neuron.
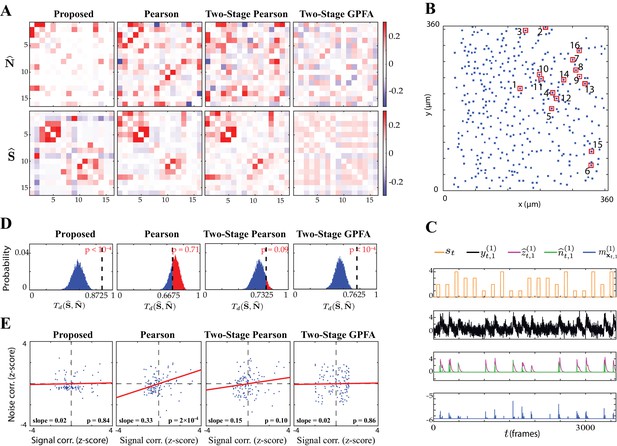
Application to experimentally-recorded data from the mouse A1.
(A) Estimated noise (top) and signal (bottom) correlation matrices using different methods. Rows from left to right: proposed method, Pearson correlations from two-photon data, two-stage Pearson and two-stage GPFA estimates. (B) Location of the selected neurons with the highest activity in the field of view. (C) Presented tone sequence (orange), observations (black), estimated calcium concentrations (purple), putative spikes (green) and estimated mean latent state (blue) in the first trial of the first neuron. (D) Null distributions of chance occurrence of dissimilarities between signal and noise correlation estimates using different methods. The observed test statistic in each case is indicated by a dashed vertical line. (E) Scatter plots of signal vs. noise correlations for individual cell pairs (blue dots) corresponding to each method. Data were normalized for comparison by computing z-scores. For each case, the linear regression model fit is shown in red, and the slope and p-value of the t-test are indicated as insets.
We estimated the Best Frequency (BF) of each neuron as the tone that resulted in the highest level of fluorescence activity. The results in Figure 4A are organized such that the neurons with the same BF are neighboring, with the BF increasing along the diagonal. Thus, expectedly (Bowen et al., 2020) our proposed method as well as the Pearson and two-stage Pearson estimates show high signal correlations along the diagonal. However, the two-stage GPFA estimates do not reveal such a structure. By visual inspection, as also observed in the simulation studies, the Pearson correlations from two-photon recordings, two-stage Pearson and two-stage GPFA estimates have significant leakage between the signal and noise correlations, whereas our proposed signal and noise correlation estimates in Figure 4A suggest distinct spatial structures.
To quantify this visual comparison, we used a statistic based on the Tanimoto similarity metric (Lipkus, 1999), denoted by for two matrices and . As a measure of dissimilarity, we used (see Performance evaluation for details). The comparison of for the four estimates is presented in the second column of Table 1. To assess statistical significance, for each comparison we obtained null distributions corresponding to chance occurrence of dissimilarities using a shuffling procedure as shown in Figure 4D, and then computed one-tailed -values from those distributions (see Performance evaluation for details). Table 1 and Figure 4D includes these p-values, which show that the proposed estimates (boldface numbers in Table 1, second column) indeed have the highest dissimilarity between signal and noise correlations. The higher leakage effect in the other three estimates is also reflected in their smaller values.
To further investigate this effect, we have depicted the scatter plots of signal vs. noise correlations estimated by each method in Figure 4E. To examine the possibility of the leakage effect on a pairwise basis, we performed linear regression in each case. The slope of the model fit, the p-value for the corresponding t-test, and the values are reported in the third and fourth columns of Table 1 (the slope and p-values are also shown as insets in Figure 4E). Consistent with the results of Winkowski and Kanold, 2013, the Pearson estimates suggest a significant correlation between the signal and noise correlation pairs (as indicated by the higher slope in Figure 4E). However, none of the other estimates (including the proposed estimates) in Figure 4E register a significant trend between signal and noise correlations. This further corroborates our assessment of the high leakage between signal and noise correlations in Pearson estimates, since such a leakage effect could result in overestimation of the trend between the signal and noise correlation pairs. The signal and noise correlations estimated by our proposed method show no pairwise trend, suggesting distinct patterns of stimulus-dependent and stimulus-independent functional connectivity (Kohn et al., 2016; Montijn et al., 2014; Rothschild et al., 2010; Keeley et al., 2020).
A key advantage of our proposed method over the Pearson and two-stage approaches is the explicit modeling of stimulus integration. The relevant parameter in this regard is the length of the stimulus integration window . While in our simulation studies the value of was known, it needs to be set by the user in real data applications. To this end, domain knowledge or data-driven methods such as cross-validation and model order selection can be utilized (see Guidelines for model parameter settings for details). Noting that the number of parameters to be estimated linearly scales with , it must be chosen large enough to capture the stimulus effects, yet small enough to result in favorable computational complexity. Here, given that the typical tone response duration of mouse A1 neurons is s (Linden et al., 2003; DeWeese et al., 2003; Petrus et al., 2014), with a sampling frequency of Hz, we surmised that a choice of suffices to capture the stimulus effects. We further examined the effect of varying on the proposed correlation estimates in Figure 4—figure supplement 1. As shown, small values of (e.g. or 10) may not be adequate to fully capture stimulus integration effects. By considering values of in the range , we observed that the correlation estimates remain stable. We thus chose for our analysis.
Careful inspection of the second panel in Figure 4C shows that the fluorescence activity often saturates to ∼4 times its baseline value. This effect is due to successive closely spaced spikes, which implies the occurrence of more than one spike per frame and thus violates our Bernoulli modeling assumption. To inspect the performance of our method more carefully under this scenario, we show in Figure 4—figure supplement 2 a zoomed-in view of the estimated latent processes (calcium concentration) and (putative spikes) for a sample data segment with high fluorescence activity. The estimated latent processes reveal two mechanisms leveraged by our inference method to mitigate the aforementioned model mismatch: first, our proposed method predicts spiking events in adjacent time frames to compensate for rapid increase in firing rate and thus infers calcium concentration levels that match the observed fluorescence; secondly, even though our generative model assumes that there is only one spiking event in a given time frame, this restriction is mitigated in our inference framework by relaxing the constraint , as explained in Low-complexity parameter updates. While this relaxation was performed for the sake of tractability of the inverse solution, it in fact leads to improved estimation results under episodes of rapid increase in firing rate, by allowing the putative spike magnitudes to be greater than 1. The latter is evident in the magnitude of the inferred spikes in Figure 4—figure supplement 2, following the rise of fluorescence activity.
Given that the ground truth correlations are not available for a direct comparison, we instead performed a test of specificity that reveals another key limitation of existing methods. Fluorescence observations exhibit structured dynamics due to the exponential intracellular calcium concentration decay (as shown in Figure 4C, for example), which are in turn related to the underlying spikes that are driven non-linearly by intrinsic/extrinsic stimuli as well as the properties of the indicator used. As such, an accurate inference method is expected to be specific to this temporal structure. To test this, we randomly shuffled the time frames consistently in the same order in all trials, in order to fully break the temporal structure governing calcium decay dynamics, and then estimated correlations from these shuffled data using the different methods. The resulting estimates of noise correlations are shown in Figure 5A for one instance of such shuffled data. The average NMSE for a total of 50 shuffled samples with respect to the original un-shuffled estimates (in Figure 4A) are tabulated in the fifth and sixth columns of Table 1, and are also indicated below each panel in Figure 5A.
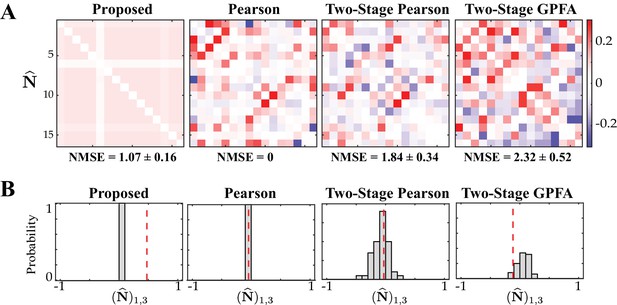
Assessing the specificity of different estimation results shown in Figure 4.
Rows from left to right: proposed method, Pearson correlations from two-photon data, two-stage Pearson and two-stage GPFA estimates. (A) The estimated noise correlations using different methods after random temporal shuffling of the observations. The mean and standard deviation of the NMSE across 50 trials are indicated below each panel. (B) Histograms of the noise correlation estimates between the first and third neurons over the 50 temporal shuffling trials. The estimate based on the original (un-shuffled) data in each case is indicated by a dashed vertical line.
A visual inspection of Figure 5A shows that the Pearson correlations from two-photon recordings expectedly remain unchanged. Since this method treats each time frame to be independent, temporal shuffling does not impact the correlations in anyway. On the other extreme, both of the two-stage estimates seem to detect highly variable and large correlation values, despite operating on data that lacks any relevant temporal structure. Our proposed method, however, remarkably produces negligible correlation estimates. Although both the two-stage and proposed estimates show variability with respect to the shuffled data (Table 1, fifth column), the standard deviation of the NMSE values of our proposed method are considerably smaller than those of the two-stage methods (Table 1, fifth column). For further inspection, the histograms of a single element () of the estimated correlation matrices across the 50 shuffling trials are shown in Figure 5B. The original un-shuffled estimates are marked by the dashed vertical lines in each case. The proposed estimate in Figure 5B is highly concentrated around zero, even though the un-shuffled estimate is non-zero. However, the two-stage estimates produce correlations that are widely variable across the shuffling trials. This analysis demonstrates that our proposed method is highly specific to the temporal structure of fluorescence observations, whereas the Pearson correlations from two-photon recordings, two-stage Pearson and two-stage GPFA methods fail to be specific.
Real data study 2: spontaneous vs. stimulus-driven activity in the mouse A1
To further validate the utility of our proposed methodology, we applied it to another experimentally-recorded dataset from the mouse A1 layer 2/3. This experiment pertained to trials of presenting a sequence of short white noise stimuli, randomly interleaved with silent trials of the same duration. Figure 6A shows a sample trial sequence. The two-photon recordings thus contained episodes of stimulus-driven and spontaneous activity (see Experimental procedures for details). Under this experimental setup, it is expected that the noise correlations are invariant across the spontaneous and stimulus-driven conditions. In accordance with the foregoing results of real data study 1, we also expect the signal and noise correlation patterns to be distinct. Each trial considered in the analysis consisted of frames (see Experimental procedures for details). We selected responsive neurons (according to the criterion described in Guidelines for model parameter settings), each with trials. Similar to real data study 1, we chose a stimulus integration window of length frames.
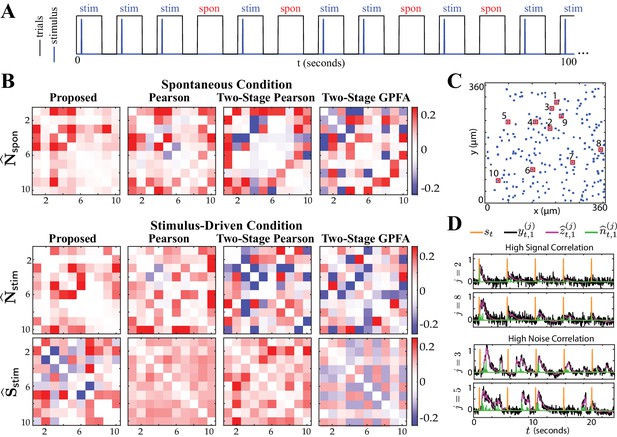
Comparison of spontaneous and stimulus-driven activity in the mouse A1.
(A) A sample trial sequence in the experiment. Stimulus-driven (stim) trials were recorded with randomly interleaved spontaneous (spon) trials of the same duration. (B) Estimated noise and signal correlation matrices under spontaneous (top) and stimulus-driven (bottom) conditions. Rows from left to right: proposed method, Pearson correlations from two-photon data, two-stage Pearson and two-stage GPFA estimates. (C) Location of the selected neurons with highest activity in the field of view. (D) Stimulus onsets (orange), observations (black), estimated calcium concentrations (purple) and putative spikes (green) for the first trial from two pairs of neurons with high signal correlation (top) and high noise correlation (bottom), as identified by the proposed estimates.
Figure 6B shows the resulting noise and signal correlation estimates under the spontaneous (, top) and stimulus-driven ( and , bottom) conditions. Figure 6C shows the spatial map of the 10 neurons considered in the analysis in the field of view. A visual inspection of the first column of Figure 6B indeed suggests that and are saliently similar, and distinct from . The Pearson correlations obtained from two-photon data (second column) and the two-stage Pearson and GPFA estimates (third and fourth columns, respectively), however, evidently lack this structure. As in the previous study, we quantified this visual comparison using the similarity metric and the dissimilarity metric (see Performance evaluation for details). These statistics are reported in Table 2 along with the p-values (null distributions are shown in Figure 6—figure supplement 1), which show that the only significant outcomes (boldface numbers) are those of our proposed method. While it is expected from the experiment design for the noise correlations under the two settings to be similar, the only method that detects this expected outcome with statistical significance is our proposed method. Moreover, the statistically significant dissimilarity between the signal and noise correlations of our proposed estimates corroborate the hypothesis that signal and noise are encoded by distinct functional networks (Kohn et al., 2016; Montijn et al., 2014; Rothschild et al., 2010; Keeley et al., 2020).
Similarity/dissimilarity metric statistics for the estimates in Figure 6.
| Estimation method | ||
|---|---|---|
| Proposed | 0.5716 () | 0.7946 () |
| Pearson | 0.3031 () | 0.5032 () |
| Two-stage Pearson | 0.2790 () | 0.7862 () |
| Two-stage GPFA | 0.2008 () | 0.7792 () |
Furthermore, Figure 6D shows the time course of the stimulus, observations, estimated calcium concentrations and putative spikes for the first trial from two pairs of neurons with high signal correlation (, top) and high noise correlation (, bottom). As expected, the putative spiking activity of the neurons with high signal correlation (top) are closely time-locked to the stimulus onsets. The activity of the two neurons with high noise correlation (bottom), however, is not time-locked to the stimulus onsets, even though the two neurons exhibit highly correlated activity. The correlations estimated via the proposed method thus encode substantial information about the inter-dependencies of the spiking activity of the neuronal ensemble.
Real data study 3: spatial analysis of signal and noise correlations in the mouse A1
Lastly, we applied our proposed method to examine the spatial distribution of signal and noise correlations in the mouse A1 layers 2/3 and 4 (data from Bowen et al., 2020). The dataset included fluorescence activity recorded during multiple experiments of presenting sinusoidal amplitude-modulated tones, with each stimulus being repeated across several trials (see Experimental procedures and Bowen et al., 2020 for experimental details). In each experiment, we selected on average around 20 responsive neurons for subsequent analysis (according to the criterion described in Guidelines for model parameter settings). For brevity, we compare the estimates of signal and noise correlations using our proposed method only with those obtained by Pearson correlations from the two-photon data. The latter method was also used in previous analyses of data from this experimental paradigm (Winkowski and Kanold, 2013).
In parallel to the results reported in Winkowski and Kanold, 2013, Figure 7A and Figure 7B illustrate the correlation between the signal and noise correlations in layers 2/3 and 4, respectively. Consistent with the results of Winkowski and Kanold, 2013, the signal and noise correlations exhibit positive correlation in both layers, regardless of the method used. However, the correlation coefficients (i.e. slopes in the insets) identified by our proposed method are notably smaller than those obtained from Pearson correlations, in both layer 2/3 (Figure 7A) and layer 4 (Figure 7B). Comparing this result with our simulation studies suggests that the stronger linear trend between the signal and noise correlations observed using the Pearson correlation estimates is likely due to the mixing between the estimates of signal and noise correlations. As such, our method suggests that the signal and noise correlations may not be as highly correlated with one another as indicated in previous studies of layer 2/3 and 4 in mouse A1 (Winkowski and Kanold, 2013).
Next, to evaluate the spatial distribution of signal and noise correlations, we plotted the correlation values for pairs of neurons as a function of their distance for layer 2/3 (Figure 7C) and layer 4 (Figure 7D). The distances were discretized using bins of length . The scatter of the correlations along with their median at each bin are shown in all panels. Then, to examine the spatial trend of the correlations, we performed linear regression in each case. The slope of the model fit, the p-value for the corresponding t-test, and the values are reported in Table 3 (the slope and p-values are also shown as insets in Figure 7C and D).
Linear regression statistics for the analysis of correlations vs. cell-pair distance.
| Statistics of layer 2/3 correlations | Statistics of layer 4 correlations | |||
|---|---|---|---|---|
| Correlations | Slope (p-value) | Value | Slope (p-value) | Value |
| Proposed Signal Corr. | () | 0.012 | () | 0.023 |
| Pearson Signal Corr. | () | 0.007 | () | 0.005 |
| Proposed Noise Corr. | () | 0.010 | () | 0.004 |
| Pearson Noise Corr. | () | 0.003 | () | 0.005 |
From Table 3 and Figure 7C and D (upper panels), it is evident that the signal correlations show a significant negative trend with respect to distance, using both methods and in both layers. However, the slope of these negative trends identified by our method (boldface numbers in Table 3) is notably steeper than those identified by Pearson correlations. On the other hand, the trends of the noise correlations with distance (bottom panels) are different between our proposed method and Pearson correlations: our proposed method shows a significant negative trend in layer 2/3, but not in layer 4, whereas the Pearson correlations of the two-photon data suggest a significant negative trend in layer 4, but not in layer 2/3. In addition, the slopes of these negative trends identified by our method (boldface numbers in Table 3) are steeper than or equal to those identified by Pearson correlations.
Our proposed estimates also indicate that noise correlations are sparser and less widespread in layer 4 (Figure 7D) than in layer 2/3 (Figure 7C). To further investigate this observation, we depicted the two-dimensional spatial spread of signal and noise correlations in both layers and for both methods in Figure 7E and F, by centering each neuron at the origin and overlaying the individual spatial spreads. The horizontal and vertical axes in each panel represent the relative dorsoventral and rostrocaudal distances, respectively, and the heat-maps represent the magnitude of correlations. Comparing the proposed noise correlation spread in Figure 7E with the corresponding spread in Figure 7F, we observe that the noise correlations in layer 2/3 are indeed more widespread and abundant than in layer 4, as can be expected by more extensive intralaminar connections in layer 2/3 vs. 4 (Watkins et al., 2014; Meng et al., 2017a; Meng et al., 2017b; Kratz and Manis, 2015).
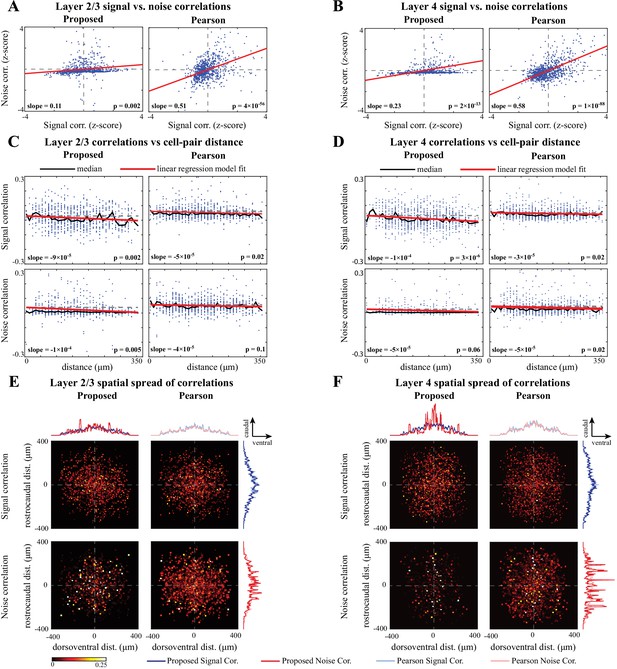
Comparison of signal and noise correlations across layers 2/3 and 4.
(A) Scatter-plot of noise vs. signal correlations (blue) for individual cell-pairs in layer 2/3, based on the proposed (left) and Pearson estimates (right). Data were normalized for comparison by computing z-scores. The linear model fits are shown in red, and the slope and p-value of the t-tests are indicated as insets. Panel (B) corresponds to layer 4 in the same organization as panel A. (C) Signal (top) and noise (bottom) correlations vs. cell-pair distance in layer 2/3, based on the proposed (left) and Pearson estimates (right). Distances were binned to intervals. The median of the distributions (black) and the linear model fit (red) are shown in each panel. The slope of the linear model fit, and the p-value of the t-test are also indicated as insets. Dashed horizontal lines indicate the zero-slope line for ease of visual comparison. Panel D corresponds to layer 4 in the same organization as panel C. (E) Spatial spread of signal (top) and noise (bottom) correlations in layer 2/3, based on the proposed (left) and Pearson estimates (right). The horizontal and vertical axes in each panel respectively represent the relative dorsoventral and rostrocaudal distances between each cell-pair, and the heat-map indicates the magnitude of correlations. Marginal distributions of the signal (blue) and noise (red) correlations along the dorsoventral and rostrocaudal axes for the proposed method (darker colors) and Pearson method (lighter colors) are shown at the top and right sides of the sub-panels. Panel F corresponds to layer 4 in the same organization as panel E.
The spatial spreads of signal and noise correlations based on the Pearson estimates are remarkably similar in both layers (Figure 7E and F, right panels), whereas they are saliently different for our proposed estimates (Figure 7E and F, left panels). This further corroborates our hypothesis on the possibility of high mixing between the signal and noise correlation estimates obtained by the Pearson correlation of two-photon data. To further examine the differences between the signal and noise correlations, the marginal distributions along the dorsoventral and rostrocaudal axes are shown in Figure 7E and F, selectively overlaid for ease of visual comparison. To quantify the differences between the spatial distributions of signal and noise correlations estimated by each method, we performed Kolmogorov-Smirnov (KS) tests on each pair of marginal distributions, which are summarized in Figure 7—figure supplement 1. Although the marginal distributions of signal and noise correlations are significantly different in all cases from both methods, the effect sizes of their difference (KS statistics) are higher for our proposed estimates compared to those of the Pearson estimates.
Finally, the spatial spreads of correlations for either method and in each layer suggest non-uniform angular distributions with possibly directional bias. To test this effect, we computed the angular marginal distributions and performed KS tests for non-uniformity, which are reported in Figure 7—figure supplement 2. These tests indicate that all distributions are significantly non-uniform. In addition, the angular distributions of both signal and noise correlations in layer 4 exhibit salient modes in the rostrocaudal direction, whereas they are less directionally selective in layer 2/3 (Figure 7—figure supplement 2).
In summary, the spatial trends identified by our proposed method are consistent with empirical observations of spatially heterogeneous pure-tone frequency tuning by individual neurons in auditory cortex (Winkowski and Kanold, 2013). The improved correspondence of our proposed method compared to results obtained using Pearson correlations could be the result of the demixing of signal and noise correlations in our method. As a result of the demixing, our proposed method also suggests that noise correlations have a negative trend with distance in layer 2/3, but are much sparser and spatially flat in layer 4. In addition, the spatial spread patterns of signal and noise correlations are more structured and remarkably more distinct for our proposed method than those obtained by the Pearson estimates.
Theoretical analysis of the bias and variance of the proposed estimators
Finally, we present a theoretical analysis of the bias and variance of the proposed estimator. Note that our proposed estimation method has been developed as a scalable alternative to the intractable maximum likelihood (ML) estimation of the signal and noise covariances (see Overview of the proposed estimation method). In order to benchmark our estimates, we thus need to evaluate the quality of said ML estimates. To this end, we derived bounds on the bias and variance of the ML estimators of the kernel for and the noise covariance . In order to simplify the treatment, we posit the following mild assumptions:
Assumption (1). We assume a scalar time-varying external stimulus (i.e. , and hence ). Furthermore, we set the observation noise covariance to be , for notational convenience.
Assumption (2). We derive the performance bounds in the regime where and are large, and thus do not impose any prior distribution on the correlations, which are otherwise needed to mitigate overfitting (see Preliminary assumptions).
Assumption (3). We assume the latent trial-dependent process and stimulus to be slowly varying signals, and thus adopt a piece-wise constant model in which these processes are constant within consecutive windows of length (i.e. and , for and with and ) for our theoretical analysis, as is usually done in spike count calculations for conventional noise correlation estimates.
Our main theoretical result is as follows:
Theorem 1 (Performance Bounds) Let , , and be fixed constants, and . Then, under Assumptions (1 - 3), the bias and variance of the maximum likelihood estimators and , conditioned on an event with satisfy:
for all , if
where and denote bounded terms that are or , and denote bounded terms that are or and and are bounded constants given in Appendix 2.
Proof. The proof of Theorem 1 is provided in Appendix 2.
■
In order to discuss the implications of this theoretical result, several remarks are in order:
Remark 1: Achieving near Oracle performance
A common benchmark in estimation theory is the performance of the idealistic oracle estimator, in which an oracle directly observes the true latent process and the true kernel dj and forms the correlation estimates. In this case, the oracle would incur zero bias and variance of order in estimating dj, and outputs an estimate of with bias and variance in the order of . Theorem 1 indeed states that for sufficiently large and small , the bias and variance of the ML estimators are arbitrarily close to those of the oracle estimator. Recall that our variational inference framework is in fact a solution technique for the regularized ML problem. Hence, the bounds in Theorem 1 provide a benchmark for the expected performance of the proposed estimators, by quantifying the excess bias and variance over the performance of the oracle estimator.
Remark 2: Effect of the observation noise and observation duration
As the assumed window of stationarity (and hence the observation duration ), the loss of performance of the proposed estimators only depends on , the variance of the observation noise. As a result, at a given observation noise variance , these bounds provide a sufficient upper bound on the time duration of the observations required for attaining a desired level of estimation accuracy. It is noteworthy that is typically small in practice, as it pertains to the effective observation noise and is significantly diminished by pixel averaging of the fluorescence traces following cell segmentation.
Remark 3: Effect of the number of trials
Finally, note that the bounds in Theorem 1 have terms that also drop as the number of trials grows. These terms in fact pertain to the performance of the oracle estimator. As the number of trials grows (), the oracle estimates become arbitrarily close to the true parameters and . Thus, our theoretical performance bounds also provide a sufficient upper bound on the number of trials required for the oracle estimator to attain a desired level of estimation accuracy.
Discussion
We developed a novel approach for the joint estimation of signal and noise correlations of neuronal activities directly from two-photon calcium imaging observations and tested our method with experimental data. Existing widely used methods either take the fluorescence traces as surrogates of spiking activity, or first recover the unobserved spikes using deconvolution techniques, both followed by computing Pearson correlations or connectivity matrices. As such, they typically result in estimates that are highly biased and are heavily dependent on the choice of the spike deconvolution technique. We addressed these issues by explicitly relating the signal and noise covariances to the observed two-photon data via a multi-tier Bayesian model that accounts for the observation process and non-linearities involved in spiking activity. We developed an efficient estimation framework by integrating techniques from variational inference and state-space estimation. We also established performance bounds on the bias and variance of the proposed estimators, which revealed favorable scaling with respect to the observation noise and trial length.
We demonstrated the utility of our proposed estimation framework on both simulated and experimentally recorded data from the mouse auditory cortex. In our simulation studies, we evaluated the robustness of our proposed method with respect to several model mismatch conditions induced by the stimulus integration model, calcium decay, SNR level, firing rate, and temporally correlated observation noise. In all cases, we observed that our proposed estimates outperform the existing methods in recovering the signal and noise correlations.
There are two main sources for the observed performance gap between our proposed method and existing approaches. The first source is the favorable soft decisions on the timing of spikes achieved by our method as a byproduct of the iterative variational inference procedure. An accurate probabilistic decoding of spikes results in better estimates of the signal and noise correlations, and conversely having more accurate estimates of the signal and noise covariances improves the probabilistic characterization of spiking events. This is in contrast with both the Pearson correlations computed from two-photon data and two-stage methods: in computing the Pearson correlations from two-photon data, spike timing is heavily blurred by the calcium decay; in the two-stage methods, erroneous hard decisions on the timing of spikes result in biases that propagate to and contaminate the downstream signal and noise correlation estimation and thus results in significant errors.
The second source of performance improvement is the explicit modeling of the non-linear mapping from stimulus and latent covariates to spiking through a canonical point process model, which is in turn tied to a two-photon observation model in a multi-tier Bayesian fashion. Our theoretical analysis in Theorem 1 corroborates that this virtue of our proposed methodology results in robust performance under limited number of trials. As we have shown in Appendix 1, as the number of trials and trial duration tend to infinity, conventional notions of signal and noise correlation indeed recover the ground truth signal and noise correlations, as the biases induced by non-linearities average out across trial repetitions. However, as exemplified in Figure 2—figure supplement 2, in order to achieve comparable performance to our method using few trials (e.g. ), the conventional correlation estimates require considerably more trials (e.g. ).
Application to two-photon data recorded from the mouse primary auditory cortex showed that unlike the aforementioned existing methods, our estimates provide noise correlation structures that are expectedly invariant across spontaneous and stimulus-driven conditions within an experiment, while producing signal correlation structures that are largely distinct from those given by noise correlation. These results provide evidence for the involvement of distinct functional neuronal network structures in encoding the stimulus-dependent and stimulus-independent information.
Our analysis of the relationship between the signal and noise correlations in layers 2/3 and 4 in mouse A1 indicated a smaller correlation between signal and noise correlations than previously reported (Winkowski and Kanold, 2013). Thus, our proposed method suggests that the signal and noise correlations reflect distinct circuit mechanisms of sound processing in layers 2/3 vs 4. The spatial distribution of signal correlations obtained by our method was consistent with previous work showing significant negative trends with distance (Winkowski and Kanold, 2013). However, in addition, our proposed method revealed a significant negative trend of noise correlations with distance in layer 2/3, but not in layer 4, in contrast to the outcome of Pearson correlation analysis. The lack of a negative trend in layer 4 could be attributed to the sparse nature of the noise correlation spread in layer 4, as revealed by our analysis of two-dimensional spatial spreads. The latter analysis indeed revealed that the noise correlations in layer 2/3 are more widespread than those in layer 4, consistent with existing work based on whole-cell patch recordings (Meng et al., 2017a; Meng et al., 2017b).
The two-dimensional spatial spreads of signal and noise correlations obtained by our method are more distinct than those obtained by Pearson correlations. The spatial spreads also allude to directionality of the functional connectivity patterns, with a notable rostrocaudal preference in layer 4. This result seems surprising in light of existing evidence for quasi-rostrocaudal organization of the tonotopic axis in mouse A1 (Romero et al., 2020). However, given the heterogeneity of tuning in both layers 2/3 and 4 with a best frequency interqartile range of ∼1–1.5 octaves over the imaging field (Bowen et al., 2020) and using supra-threshold tones, we expect that the tones will drive not only neurons with the corresponding best frequency, but also neurons tuned to neighboring frequencies. Moreover, there is high connectivity between layer 4 cells within a few 100 μm across the tonotopic axis (Kratz and Manis, 2015; Meng et al., 2017a), potentially amplifying and broadening the effect of supra-threshold tones.
Our proposed method can scale up favorably to larger populations of neurons, thanks to the underlying low-complexity variational updates in the inference procedure. Due to its minimal dependence on training data, our estimation framework is also applicable to single-session analysis of two-photon data with limited number of trials and duration. Another useful byproduct of the proposed framework is gaining access to approximate posterior densities in closed-form, which allows further statistical analyses such as construction of confidence intervals. Our proposed methodology can thus be used as a robust and scalable alternative to existing approaches for extracting neuronal correlations from two-photon calcium imaging data.
A potential limitation of our proposed generative model is the assumption that there is at most one spiking event per time frame for each neuron, in light of the fact that typical two-photon imaging frame durations are in the range of 30–100 ms. Average spike rates of excitatory neurons in mouse A1 layers 2/3 and 4 are of the order of Hz (Petrus et al., 2014; Forli et al., 2018) and thus our model is reasonable for the current study, although it might not be optimal during bursting activity. It is noteworthy that we relax this assumption in the inference framework by allowing the magnitude of putative spikes to be greater than one, thus alleviating the model mismatch during episodes of rapid increase in firing rate. This assumption can also be made more precise by adopting a Poisson model, but that would render closed-form variational density updates intractable.
Furthermore, in the regime of extremely low spiking rate and high observation noise, the proposed method may fail to capture the underlying correlations faithfully and its performance degrades to those of existing methods based on Pearson correlations, as we have shown through our simulation studies. Nevertheless, our method addresses key limitations of conventional signal and noise correlation estimators that persist even in high spiking rate and high SNR conditions.
Our proposed estimation framework can be used as groundwork for incorporating other notions of correlation such as the connected correlation function (Martin et al., 2020), and to account for non-Gaussian and higher order structures arising from spatiotemporal interactions (Kadirvelu et al., 2017; Yu et al., 2011). Other possible extensions of this work include leveraging variational inference beyond the mean-field regime (Wang and Blei, 2013), extension to time-varying correlations that underlie rapid task-dependent dynamics, and extension to non-linear models such as those parameterized by neural networks (Aitchison et al., 2017). In the spirit of easing reproducibility, a MATLAB implementation of our proposed method as well as the data used in this work are made publicly available (Rupasinghe, 2020; Rupasinghe et al., 2021).
Materials and methods
Proposed forward model
Request a detailed protocolSuppose we observe fluorescence traces of neurons, for a total duration of discrete-time frames, corresponding to independent trials of repeated stimulus. Let , , and be the vectors of noisy observations, intracellular calcium concentrations, and ensemble spiking activities, respectively, at trial and frame . We capture the dynamics of by the following state-space model:
where represents the scaling of the observations, is zero-mean i.i.d. Gaussian noise with covariance , and is the state transition parameter capturing the calcium dynamics through a first order model. Note that this state-space is non-Gaussian due to the binary nature of the spiking activity, that is, . We model the spiking data as a point process or Generalized Linear Model with Bernoulli statistics (Eden et al., 2004; Paninski, 2004; Smith and Brown, 2003; Truccolo et al., 2005):
where is the conditional intensity function (Truccolo et al., 2005), which we model as a non-linear function of the known external stimulus and the other latent intrinsic and extrinsic trial-dependent covariates, . While we assume the stimulus to be common to all neurons, we model the distinct effect of this stimulus on the neuron via an unknown kernel , akin to the receptive field.
The non-linear mapping of our choice is the logistic link, which is also the canonical link for a Bernoulli process in the point process and Generalized Linear Model frameworks (Truccolo et al., 2005). Thus, we assume:
Finally, we assume the latent trial dependent covariates to be a Gaussian process , with mean and covariance .
The probabilistic graphical model in Figure 8 summarizes the main components of the aforementioned forward model. According to this forward model, the underlying noise covariance matrix that captures trial-to-trial variability can be identified as . The signal covariance matrix, representing the covariance of the neural activity arising from the repeated application of the stimulus , is given by , where . The signal and noise correlation matrices, denoted by and , can then be obtained by standard normalization of and :
The main problem is thus to estimate from the noisy and temporally blurred data .
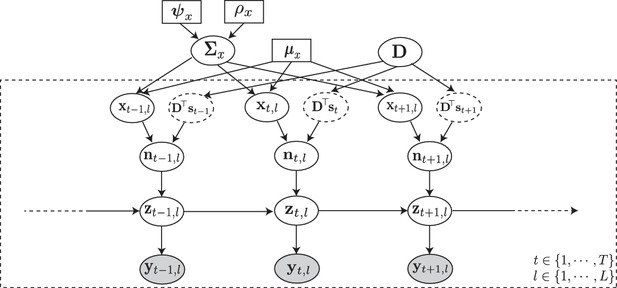
Probabilistic graphical model of the proposed forward model.
The fluorescence observations at the time frame and trial: , are noisy surrogates of the intracellular calcium concentrations: . The calcium concentration at time is a function of the spiking activity , and the calcium activity at the previous time point . The spiking activity is driven by two independent mechanisms: latent trial-dependent covariates , and contributions from the known external stimulus , which we model by (in which the receptive field is unknown). Then, we model as a Gaussian process with constant mean , and unknown covariance . Finally, we assume the covariance to have an inverse Wishart prior distribution with hyper-parameters and . Based on this forward model, the inverse problem amounts to recovering the signal and noise correlations by directly estimating and (top layer) from the fluorescence observations (bottom layer).
Overview of the proposed estimation method
Request a detailed protocolFirst, given a limited number of trials from an ensemble with typically low spiking rates, we need to incorporate suitable prior assumptions to avoid overfitting. Thus, we impose a prior on the noise covariance, to compensate sparsity of data. A natural estimation method to estimate in a Bayesian framework is to maximize the observed data likelihood , that is maximum likelihood (ML). Thus, we consider the joint likelihood of the observed data and latent processes to perform Maximum a Posteriori (MAP) estimation:
Inspecting this MAP problem soon reveals that estimating and is a challenging task: (1) standard approaches such as Expectation-Maximization (EM) (Shumway and Stoffer, 1982) are intractable due to the complexity of the model, arising from the hierarchy of latent processes and the non-linearities involved in their mappings and (2) the temporal coupling of the likelihood in the calcium concentrations makes any potential direct solver scale poorly with .
Thus, we propose an alternative solution based on Variational Inference (VI) (Beal, 2003; Blei et al., 2017; Jordan et al., 1999). VI is a method widely used in Bayesian statistics to approximate unwieldy posterior densities using optimization techniques, as a low-complexity alternative strategy to Markov Chain Monte Carlo sampling (Hastings, 1970) or empirical Bayes techniques such as EM. To this end, we treat and as latent variables and and as unknown parameters to be estimated. We introduce a framework to update the latent variables and parameters sequentially, with straightforward update rules. We will describe the main ingredients of the proposed framework in the following subsections. Hereafter, we use the shorthand notations , , and .
Preliminary assumptions
Request a detailed protocolFor the sake of simplicity, we assume that the constants α, , and are either known or can be consistently estimated from pilot trials. Next, we take to be an Inverse Wishart density:
which turns out to be the conjugate prior in our model. Thus, and will be the hyper-parameters of our model. Procedures for hyper-parameter tuning and choosing the key model parameters are given in subsections Hyper-parameter tuning and Guidelines for model parameter settings, respectively.
Decoupling via Pólya-Gamma augmentation
Request a detailed protocolDirect application of VI to problems containing both discrete and continuous random variables results in intractable densities. Specifically, finding a variational distribution for in our model with a standard distribution is not straightforward, due to the complicated posterior arising from co-dependent Bernoulli and Gaussian random variables. In order to overcome this difficulty, we employ Pólya-Gamma (PG) latent variables (Pillow and Scott, 2012; Polson et al., 2013; Linderman et al., 2016). We observe from Equation 4 that the posterior density, is conditionally independent in with:
Thus, upon careful inspection, we see that this density has the desired form for the PG augmentation scheme (Polson et al., 2013). Accordingly, we introduce a set of auxiliary PG-distributed i.i.d. latent random variables , for , and , to derive the complete data log-likelihood:
where and accounts for terms not depending on , and . The complete data log-likelihood is notably quadratic in , which as we show later admits efficient estimation procedures with favorable scaling in .
Deriving the optimal variational densities
Request a detailed protocolIn this section, we will outline the procedure of applying VI to the latent variables and , assuming that the parameter estimates and of the previous iteration are available. The methods that we propose to update the parameters and subsequently, will be discussed in the next section.
The objective of variational inference is to posit a family of approximate densities over the latent variables, and to find the member of that family that minimizes the Kullback-Leibler (KL) divergence to the exact posterior:
However, evaluating the KL divergence is intractable, and it has been shown (Blei et al., 2017) that an equivalent result to this minimization can be obtained by maximizing the alternative objective function, called the evidence lower bound (ELBO):
Further, we assume to be a mean-field variational family (Blei et al., 2017), resulting in the overall variational density of the form:
Under the mean field assumptions, the maximization of the ELBO can be derived using the optimization algorithm ‘Coordinate Ascent Variational Inference’ (CAVI) (Bishop, 2006; Blei et al., 2017). Accordingly, we see that the optimal variational densities in Equation 6 take the forms:
Upon evaluation of these expectations, we derive the optimal variational distributions as:
whose parameters , , , , and can be updated given parameter estimates and :
and , with denoting a diagonal matrix with entries and denoting the vector of all ones.
Low-complexity parameter updates
Request a detailed protocolNote that even though is composed of the latent processes , we do not use VI for its inference, and instead consider it as an unknown parameter. This choice is due to the temporal dependencies arising from the underlying state-space model in Equation 4, which hinders a proper assignment of variational densities under the mean field assumption. We thus seek to estimate both and using the updated variational density .
First, note that the log-likelihood in Equation 5 is decoupled in , which admits independent updates to , for . As such, given an estimate , we propose to estimate as:
under the constraints , for and . These constraints are a direct consequence of being a Bernoulli random variable with . While this problem is a quadratic program and can be solved using standard techniques, it is not readily decoupled in , and thus standard solvers would not scale favorably in .
Instead, we consider an alternative solution that admits a low-complexity recursive solution by relaxing the constraints. To this end, we relax the constraint and replace the constraint by penalty terms proportional to . The resulting relaxed problem is thus given by:
where with being a hyper-parameter. Given that the typical spiking rates are quite low in practice, is expected to be a negative number. Thus, we have assumed that .
The problem of Equation 7 pertains to compressible state-space estimation, for which fast recursive solvers are available (Kazemipour et al., 2018). The solver utilizes the Iteratively Re-weighted Least Squares (IRLS) (Ba et al., 2014) framework to transform the absolute value in the second term of the cost function into a quadratic form in , followed by Fixed Interval Smoothing (FIS) (Rauch et al., 1965) to find the minimizer. At iteration , given a current estimate , the problem reduces to a Gaussian state-space estimation of the form:
with and , where is a diagonal matrix with , for some small constant . This problem can be efficiently solved using FIS, and the iterations proceed for a total of times or until a standard convergence criterion is met (Kazemipour et al., 2018). It is noteworthy that our proposed estimator of the calcium concentration can be thought of as soft spike deconvolution, which naturally arises from our variational framework, as opposed to the hard spike deconvolution step used in two-stage estimators.
Finally, given and the updated , the estimate of for can be updated in closed-form by maximizing the expected complete log-likelihood :
The VI procedure iterates between updating the variational densities and parameters until convergence, upon which we estimate the noise and signal covariances as:
The overall combined iterative procedure is outlined in Algorithm 1. Furthermore, a MATLAB implementation of this algorithm is publicly available in Rupasinghe, 2020. It is worth noting that a special case of our proposed variational inference procedure can be used to estimate signal and noise correlations from electrophysiology recordings. Given that spiking activity, that is , is directly observed in this case, the solution to the optimization problem in Equation (7) is no longer required. Thus, the parameters and can be estimated using a simplified variational procedure, which is outlined in Algorithm 2 in Appendix 3.
Guidelines for model parameter settings
There are several key model parameters that need to be set by the user prior to the application of our proposed method. Here, we provide our rationale and criteria for choosing these parameters, which could also serve as guidelines in facilitating the applicability and adoption of our method by future users. We will also provide the specific choices of these parameters used in our simulation studies and real data analyses.
Number of neurons selected for the analysis ()
Request a detailed protocolWhile our proposed method scales-up well with the population size due to low-complexity update rules involved, including neurons with negligible spiking activity in the analysis would only increase the complexity and potentially contaminate the correlation estimates. Thus, we performed an initial pre-processing step to extract neurons that exhibited at least one spiking event in at least half of the trials considered.
Stimulus integration window length ()
Request a detailed protocolThe number of lags considered in stimulus integration is a key parameter that can be set through data-driven approaches or using prior domain knowledge. Examples of common data-driven criteria include cross-validation, Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), which balance the estimation accuracy and model complexity (Arlot and Celisse, 2010; Ding et al., 2018).
To quantify the effect of on model complexity, we first describe the stimulus encoding model in our framework. Suppose that the onset of the tone in the stimulus set (, where is the number of distinct tones) is given by a binary sequence . The choice of implies that the response at time post-stimulus depends only on the most recent time lags. As such, the effective stimulus at time corresponding to tone is given by . By including all the tones, the overall effective stimulus at the time frame is given by . The stimulus modulation vector would thus be -dimensional. As a result, the number of parameters () to be estimated linearly increases with . By using additional domain knowledge, we chose to be large enough to capture the stimulus effects, and at the same time to be small enough to control the complexity of the algorithm.
As an example, given that the typical tone response duration of mouse primary auditory neurons is s (Linden et al., 2003; DeWeese et al., 2003; Petrus et al., 2014), with a sampling frequency of Hz, a choice of would suffice to capture the stimulus effects. By further examining the effect of varying on the proposed correlation estimates in Figure 4—figure supplement 1, we chose for our real data analyses.
Observation noise covariance () and scaling matrix ()
Request a detailed protocolWe assumed that the observation noise covariance is diagonal, and estimated the diagonal elements using the background fluorescence in the absence of spiking events, for each neuron. We set , where represents the identity matrix, and estimated by considering the average increase in fluorescence after the occurrence of isolated spiking events. Specifically, we derived the average fluorescence activity of multiple trials triggered to the fluorescence rise onset, and set as the increment in the magnitude of this average fluorescence immediately following the rise onset.
State transition parameter (α)
Request a detailed protocolWe chose α in the range , which match the slow dynamics of the calcium indicator in our data. We tested the robustness of our estimates under different choices of α in this range through the method outlined in Hyper-parameter tuning, and accordingly chose the optimal value of α.
Mean of the latent trial-dependent process ()
Request a detailed protocolWe estimated as a constant that is proportional to the average firing rate. To this end, we parametrized each component of as , for . The constants and were chosen such that , which gives the range of baseline parameters compatible with observed firing rates in our experimental data.
Parameter choices for simulation study 1
Request a detailed protocolIn the first simulation study, we set , , , and ( represents the identity matrix and represents the vector of all ones), so that the SNR of simulated data was in the same range as that of experimentally-recorded data. We used a order autoregressive process with a mean of -1 as the stimulus (st), and considered () lags of the stimulus (i.e. ) in both the generative model and inference procedure. The components of the linear and quadratic stimulus modulation vectors, that is , and , were chosen at random uniformly in the range . The variance of st was set in each case such that the average power of the overall signal component ( for the linear model, and for the non-linear model) was comparable to the average power of the noise component ().
| Algorithm 1 Estimation of and through the proposed iterative procedure |
|---|
| Inputs: Ensemble of fluorescence measurements , constants and , hyper-parameters , , β and , tolerance at convergence δ and the external stimulus Outputs: and Initialization: Initial choice of , , and , , 1: while do Estimate calcium concentrations using Fixed Interval Smoothing 2: for do Forward filter: 3: for do 4: 5: 6: 7: 8: 9: end for Backward smoother: 10: for do 11: 12: end for 13: end for Update variational parameters 14: for and do 15: 16: 17: 18: for do 19: 20: 21: end for 22: end for 23: Update IRLS covariance approximation 24: for and do 25: 26: end for Update outputs and the convergence criterion 27: for do 28: 29: end for 30: , 31: , 32: 33: end while 34: Return and |
Parameter choices for simulation study 2
Request a detailed protocolIn the second simulation study, we set , , and ( represents the identity matrix and represents the vector of all ones) when generating the fluorescence traces , so that the SNR of the simulated data was in the same range as of real calcium imaging observations. Furthermore, we simulated the spike trains based on a Poisson process (Smith and Brown, 2003) using the discrete time re-scaling procedure (Brown et al., 2002; Smith and Brown, 2003). Following the assumptions in Brown et al., 2002, we used an exponential link to simulate the observations:
as opposed to the Bernoulli-logistic assumption in our recognition model. Then, we estimated the noise covariance using the Algorithm 1, with a slight modification. Since there are no external stimuli, we set and . Accordingly, in Algorithm 1, we initialized and did not perform the update on in the subsequent iterations.
Parameter choices for real data study 1
Request a detailed protocolThe dataset consisted of recordings from 371 excitatory neurons, from which we selected responsive neurons for the analysis. Each trial consisted of time frames (the sampling frequency was 30 Hz, and each trial had a duration of 120 s), with the presentation of a random sequence of four tones (). The spiking events were very sparse and infrequent, and hence this dataset fits our model with at most one spiking event in a time frame.
We considered () time lags in this analysis and further examined the effect of varying in Figure 4—figure supplement 1. We set and ( represents the identity matrix).
Parameter choices for real data study 2
Request a detailed protocolEach trial consisted of frames (25.5 s) at a sampling frequency of 30 Hz. The A1 neurons studied here had low response rates (in both time and space), with only neurons exhibiting spiking activity in at least half of the trials. Thus, we selected neurons and trials for the analysis, and chose lags of the stimulus () in the model for the stimulus-driven condition. We set and ( represents the identity matrix).
Parameter choices for real data study 3
Request a detailed protocolEach experiment consisted of trials of different tone frequencies repeated at four different amplitude levels, resulting in each concatenated trial being s long (see Bowen et al., 2020 for more details). We set the number of stimulus time lags considered to be (). For each layer, we analyzed fluorescence observations from six experiments. In each experiment, we selected the most responsive neurons for the subsequent analysis. We set and .
Performance evaluation
Simulation studies
Request a detailed protocolSince the ground truth is known in simulations, we directly compared the performance of each signal and noise correlation estimate with the ground truth signal and noise correlations, respectively. Suppose the ground truth correlations are given by the matrix and the estimated correlations are given by the matrix . To quantify the similarity between and , we defined the following two metrics:
Normalized Mean Squared Error (NMSE): The NMSE computes the mean squared error of with respect to using the Frobenius Norm:
Ratio between out-of-network power and in-network power (leakage): First, we identified the in-network and out-of-network components from the ground truth correlation matrix . Suppose that if the true correlation between the neuron and the neuron is non-zero, then , for some . Thus, we formed a matrix that masks the in-network components, by setting if and if . Likewise, we also formed a matrix that masks the out-of-network components, by setting if and if . Then, using these two matrices we quantified the leakage effect of comparative to by:
where denotes element-wise multiplication.
Real data studies
Request a detailed protocolTo quantify the similarity and dissimilarity between signal and noise correlation estimates, we used a statistic based on the Tanimoto similarity metric (Lipkus, 1999), denoted by for two matrices and . For two vectors and with non-negative entries, the Tanimoto coefficient (Lipkus, 1999) is defined as:
The Tanimoto similarly metric between two matrices can be defined in a similar manner, by vectorizing the matrices. Thus, we formulated a similarity metric between two correlation matrices and as follows. Let and , with the operator interpreted element-wise. Note that , and have non-negative entries. We then defined the similarity matrix by combining those of the positive and negative parts as follows:
where denotes the percentage of positive entries in and . As a measure of dissimilarity, we used . The values of in Table 1 and and reported in Table 2 were obtained based on the foregoing definitions.
To further assess the statistical significance of these results, we performed following randomized tests. To test the significance of , for each comparison and each algorithm, we fixed the first matrix (i.e. ) and randomly shuffled the entries of the second one (i.e. ) while respecting symmetry. We repeated this procedure for 10000 trials, to derive the null distributions that represented the probabilities of chance occurrence of similarities between two random groups of neurons.
To test the significance of and , for each comparison and each algorithm, again we fixed the first matrix (i.e. signal correlations). Then, we formed the elements of the second matrix (akin to noise correlations) as follows. For each element of the second matrix, we assigned either the same element as the signal correlations (in order to model the leakage effect) or a random noise (with same variance as the elements in the noise correlation matrix) with equal probability. As before, we repeated this procedure for 10,000 trials, to derive the null distributions that represent the probabilities of chance occurrence of dissimilarities between two matrices that have some leakage between them.
Hyper-parameter tuning
Request a detailed protocolThe hyper-parameters that directly affect the proposed estimation are the inverse Wishart prior hyper-parameters: and . Given that appears in the form of , we will consider and as the main hyper-parameters for simplicity. Here, we propose a criterion for choosing these two hyper-parameters in a data-driven fashion, which will then be used to construct the estimates of the noise covariance matrix and weight matrix . Due to the hierarchy of hidden layers in our model, an empirical Bayes approach for hyper-parameter selection using a likelihood-based performance metric is not straightforward. Hence, we propose an alternative empirical method for hyper-parameter selection as follows.
For a given choice of and , we estimate and following the proposed method. Then, based on the generative model in Proposed forward model, and using the estimated values of and , we sample an ensemble of simulated fluorescence traces , and compute the metric :
where denotes the empirical covariance and . Note that is strictly convex in . Thus, minimizing over for a given has a unique solution. Accordingly, we observe that is minimized when is nearest to . Therefore, the corresponding estimates and that generated , best match the second-order statistics of that was generated by the true parameters and .
The typically low spiking rate of sensory neurons observed in practice may render the estimation problem ill-posed. It is thus important to have an accurate choice of the scale matrix in the prior distribution. However, an exhaustive search for optimal tuning of is not computationally feasible, given that it has free variables. Thus, the main challenge here is finding the optimal choice of the scale matrix .
To address this challenge, we propose the following method. First, we fix , where τ is a scalar and is the identity matrix. Next, given we find the optimal choice of as:
where is a finite set of candidate solutions for . Let denote the noise covariance estimate corresponding to hyper-parameters . We will next use to find a suitable choice of . To this end, we first fix , for some . Note that by choosing to be much smaller than , the final estimates become less sensitive to the choice of . Then, we construct a candidate set for by scaling with a finite set of scalars , i.e. . To select , we match it with the choice of by solving:
Finally, we use these hyper-parameters to obtain the estimators and as the output of the algorithm.
Experimental procedures
All procedures were approved by the University of Maryland Institutional Animal Care and Use Committee. Imaging experiments were performed on a P60 (for real data study 1) and P83 (for real data study 2) female F1 offspring of the CBA/CaJ strain (The Jackson Laboratory; stock #000654) crossed with transgenic C57BL/6J-Tg(Thy1-GCaMP6s)GP4.3Dkim/J mice (The Jackson Laboratory; stock #024275) (CBAxThy1), and F1 (CBAxC57). The third real data study was performed on data from P66-P93 and P166-P178 mice (see Bowen et al., 2020 for more details). We used the F1 generation of the crossed mice because they have good hearing into adulthood (Frisina et al., 2011).
We performed cranial window implantation and two-photon imaging as previously described in Francis et al., 2018; Liu et al., 2019; Bowen et al., 2019. Briefly, we implanted a cranial window of 3 mm in diameter over the left auditory cortex. We used a scanning microscope (Bergamo II series, B248, Thorlabs) coupled to Insight X3 laser (Spectra-physics) (study 1) or pulsed femtosecond Ti:Sapphire two-photon laser with dispersion compensation (Vision S, Coherent) (studies 2 and 3) to image GCaMP6s fluorescence from individual neurons in awake head-fixed mice with an excitation wavelengths of nm and nm, respectively. The microscope was controlled by ThorImageLS software. The size of the field of view was . Imaging frames of pixels (pixel size ) were acquired at 30 Hz by bidirectional scanning of an 8 kHz resonant scanner. The imaging depth was around below pia.
Data pre-processing
Request a detailed protocolA circular ROI was manually drawn over each cell body to extract raw fluorescence traces from individual cells. Neuropil contamination subtraction and baseline correction were performed on the raw fluorescence traces of each cell (Francis et al., 2018; Liu et al., 2019; Bowen et al., 2020) according to , where was set to 0.7 in real data study 1 (Francis et al., 2018), 0.8 in real data study 2 (Liu et al., 2019) and 0.9 in real data study 3 (Bowen et al., 2020). The two-photon observations used in our analyses are the output of this pre-processing step.
Stimuli for real data study 1
Request a detailed protocolDuring imaging experiments, we presented four tones (4, 8, 16, and 32 kHz) at 70 dB SPL. The tones were 2 s in duration with an inter-trial silence of 4 s. For the sequence of tones, we first generated a randomized sequence that consisted of five repeats for each tone (20 tones in total) and then the same sequence was repeated for 10 trials.
Stimuli for real data study 2
Request a detailed protocolDuring imaging experiments, we presented a 75 dB SPL 100 ms broadband noise (4–48 kHz) as the auditory stimulus. Each trial was 5.1 s long (1 s pre-stimulus silence + 0.1 s stimulus + 3 s post-stimulus silence), and the inter-trial duration was 3 s. Spontaneous neuronal activity was collected from activity during randomly interleaved no-stimuli trials of the same duration, and these trials had complete silence throughout the trial duration (5.1 s long).
Then, we extracted 50 such trials from each type, and formed 10 () trials each of 25.5 s duration ( frames) for the subsequent analysis, by concatenating five 5.1 s trials. This final step was performed to increase the effective trial duration.
Stimuli for real data study 3
Request a detailed protocolDuring imaging experiments, sounds were played at four sound levels (20, 40, 60, and 80 dB SPL). Auditory stimuli consisted of sinusoidal amplitude-modulated (SAM) tones (20 Hz modulation, cosine phase), ranging from 3 to 48 kHz. The frequency resolution was two tones/octave (0.5 octave spacing) and each of these tonal stimuli was 1 s long, repeated five times with a 4−6 s inter-stimulus interval (see Bowen et al., 2020 for details).
Appendix 1
Relationship to existing definitions of Signal and Noise correlations
Recall that the conventional definitions of signal and noise covariance of spiking activity between the and neuron are (Lyamzin et al., 2015):
where , is the empirical covariance. The correlations, are then derived by the standard normalization:
Suppose that the spiking events follow the forward model:
where is a differentiable non-linear mapping. We assume and to be independent. Without loss of generality, let and . Further, we define the notation to denote almost sure equivalence, that is and for some random variable .
First, let us consider . Noting that and , we conclude as :
from the law of large numbers. Then, if we consider the Taylor series expansion of around the mean , we get:
where and represent the higher order terms. Then, as , we get:
since by the Law of Large numbers. Thus, we see that:
where is a constant and is typically small if the latent process and the stimulus are concentrated around their means. Then, the signal correlations are obtained by normalization of the signal covariance as in Equation 9, through which the scaling factor cancels and we get:
Thus, as , we see that is indeed the signal correlation matrix that is aimed to be approximated by the conventional definitions.
Next, let us consider . Similar to foregoing analysis of the signal covariance, as we get:
Then, from a Taylor series expansion, we get:
where and represent the higher order terms. Then, as :
from the law of large numbers. Accordingly, we see that:
where is a constant and is typically small if the latent process and the stimulus are concentrated around their means. Then, the noise correlations are derived by normalization of the noise covariance given in Equation 9. This cancels out the scaling factor , and we get:
Thus, we similarly conclude that as , the conventional definition of noise correlation indeed aims to approximate .
As a numerical illustration, we demonstrated in Figure 2—figure supplement 2 that the conventional definitions of the correlations indeed approximate our proposed definitions, but require much larger number of trials to be accurate. More specifically, in order to achieve comparable performance to our method using trials, the conventional correlation estimates require trials.
Appendix 2
Proof of Theorem 1
In what follows, we present a comprehensive proof of Theorem 1. Recall the following key assumptions:
Assumption (1). We assume a scalar time-varying external stimulus (i.e. , and hence ). Furthermore, we set the observation noise covariance to be , for notational convenience.
Assumption (2). We derive the performance bounds in the regime where and are large, and thus do not impose any prior distribution on the correlations (i.e. ), which are otherwise needed to mitigate overfitting (see Preliminary assumptions).
Assumption (3). We assume the latent trial-dependent process and stimulus to be slowly varying signals, and thus adopt a piece-wise constant model in which these processes are constant within consecutive windows of length (i.e., and , for and with and ) for our theoretical analysis, as is usually done in spike count calculations for conventional noise correlation estimates.
Proof of Theorem 1. First, recall the proposed forward model (see Proposed forward model) under Assumption (1 – 3):
where , is the logistic function. Note that we have re-defined the latent process by absorbing the stimulus activity to the mean of for notational convenience, without loss of generality. Hereafter, we also assume that without loss of generality. For a truncation level (to be specified later), consider the event
such that .
First, we derive convenient forms of the maximum likelihood estimators via the Laplace’s approximations and asymptotic expansions (Wong, 2001) through the following lemma:
Lemma 1
Conditioned on event , the maximum likelihood estimators of the stimulus kernel of the neuron and the noise covariance between the and neurons take the forms:
where
with
Proof of Lemma 1.
First, maximizing the data likelihood, we derive the estimators:
and
where . Then, we simplify these integrals based on the saddle point method of asymptotic expansions (Wong, 2001). To that end, first consider the numerator of Equation 10 denoted by . First, we evaluate the integration in with respect to the variable . To that end, note:
where , , and is shorthand notation for the product measure of the discrete random vector . Observing that for , using the method of asymptotic expansions, can be evaluated as:
where the determinant of the Hessian matrix , is a negative function of α. Note that the covariance of this Gaussian integral is a function of , and hence is bounded. Thus, all higher order error terms in Equation 12 are also bounded, as higher order moments of Gaussian distributions are functions of the covariance.
Next, we simplify the integral in Equation 12 using a similar procedure. We have:
where with
and . Then, we note that the gradient of f2, for , where . Accordingly, by re-applying the saddle point method of asymptotic expansions, we evaluate the integral in Equation 13 as:
where the determinant of the Hessian, when conditioned on event . The higher order terms in Equation 14 will be bounded if the covariance of the saddle point approximation is bounded, which we ensure by conditioning on event . This completes the evaluation of .
Following the same sequence of arguments, we evaluate the denominator of Equation 10 denoted by . Accordingly, we derive:
where Finally, by combining Equation 12, Equation 14 and Equation 15, the maximum likelihood estimator in Equation 10 takes the form:
Further, following the same sequence of reasoning, simplifying the numerator and denominator of Equation 11 yields:
This concludes the proof of Lemma 1. ■
Given that is unbounded for or , we consider another truncation: , where . This choice of guarantees that over , for all , and : and thus on .
From Lemma 1, the bias and variance of the maximum likelihood estimators, and are upper-bounded, if those of and are bounded:
and
where , , and represent terms that are or . Thus, we seek to derive the performance bounds of and .
Bounding the bias of
Let us first consider . Note that:
where holds since the Oracle estimator, (i.e., observing directly) is unbiased and follows through the application of Jensen’s inequality and triangle inequality. To simplify this bound, the triangle inequality yields:
Then, to bound each of these terms, we establish a piece-wise linear Lipschitz-type bound on . First, consider the first term . We seek to upper-bound this expectation by bounding via the following technical lemma:
Lemma 2. Conditioned on event , the following bound holds for all , and :
where
Proof of Lemma 2. First, consider the case . We bound the function in a piece-wise fashion as follows. Note that is convex for and concave for . Thus, it immediately follows that for , is convex and hence:
Furthermore, for , is concave, and hence is bounded by the tangent at :
Finally, for the case of , consider the line,
From the convexity of , upper bounds for , since for . Combining the piece-wise bounds in Equation 20, Equation 21 and Equation 22, we conclude that for :
where
Due to the symmetry of , the same bound in Equation 23 can be established for as well.
Then, using and conditioning on event , we simplify this bound as:
Finally, based on the fact that , the latter is further upper bounded as:
where
This concludes the proof of Lemma 2. ■
Following Lemma 2, by conditioning on the event we have:
Then, we note that:
where in we have used the Cauchy-Schwarz inequality, and in we have used the fact that the observation noise across the time instances is i.i.d. and white. From the bounds in Equation 24 and Equation 25, we conclude that the first expectation in Equation 19, conditioned on event is bounded as:
The foregoing sequence of reasoning similarly follows for , since for , and (as a consequence of for , and , conditioned on ). Accordingly, we derive the upper bound on the second term in Equation 19, conditioned on event :
where follows from the application of Jensen’s inequality, follows from the formula for the variance of a Binomial random variable, and follows from the inequality , for . Combining the results in Equation 26 and Equation 27, the overall expectation in Equation 19, conditioned on the event is upper-bounded by:
where we have lower bounded the probability of the event by (that is, ). Thus, from Equation 18 and Equation 28 we derive:
where in we have used the Cauchy-Schwarz inequality while defining .
Then, for , we have and . Let for some . Further, for some , suppose that:
Under these conditions,
where in we have used the fact that for . Thus, under the conditions in Equation 29, we have:
Finally, from Equation 16 and Equation 31, we conclude that:
where .
Bounding the variance of
Next, we prove the upper bound on the variance of the maximum likelihood estimator, . To that end, we upper-bound the variance of . First, using the Cauchy-Schwarz inequality, we have:
Then, we upper-bound the conditional second moment of using the same techniques as we used in bounding the first moment. Accordingly, we get:
where in , we have used the Cauchy-Schwarz inequality and follows from , which can be proven by the same techniques as before.
Next, we note that the variance of the Oracle estimator is given by:
Combining Equation 32, Equation 33, and Equation 34, we can upper-bound the conditional variance of following Equation 32 as:
Then, following Equation 16, under the conditions for in Equation 29, we conclude the proof of the conditional variance of :
where .
Bounding the bias of
Next, following the foregoing techniques, we upper-bound the bias and variance of the noise covariance estimator . To that end, we first note:
where follows from the triangle inequality, with the Oracle noise covariance estimator (i.e., observing directly), being defined as:
Then, to simplify the first term in Equation 36, we use similar techniques as before. Accordingly,
where follows through the application of Jensen’s inequality and triangle inequality. Next, conditioned on the event we have:
where and we have used . Similarly, conditioned on the event the second term in Equation 37 can be bounded as:
Then, by combining the bounds in Equation 38 and Equation 40 and using an instance of Cauchy-Schwarz inequality , we see that the bound in Equation 37 conditioned on the event can be expressed as:
Next, we see that the oracle estimator follows an Inverse Wishart distribution, that is . Therefore, we get:
Thus, the bias of the oracle estimator is given by:
Combining the results in Equation 41 and Equation 42, the bias of can be bounded as:
Finally, under the conditions for in Equation 29, the latter inequality simplifies to:
where in we have used and and in we have used , which follows from Equation 30. Thus, following Equation 17 we derive the bound on the bias of the maximum likelihood estimator:
where .
Bounding the variance of
Next, we establish an upper bound on the variance of the maximum likelihood estimator of the noise covariance. To that end, we upper-bound the variance of . First, using the Cauchy-Schwarz inequality, we get:
Then, we upper-bound the conditional second moment of using the same techniques used in bounding its first moment. Accordingly, we derive:
where the last bound follows from the Cauchy-Schwarz inequality. Then, we derive:
Using the final bound of Equation 47 in Equation 46, we get:
where the last inequality follows from an instance of the Cauchy-Schwarz inequality, that is .
Then, following the observation , we derive the variance of :
Combining Equation 45, Equation 48 and Equation 49, we express the upper bound on the conditional variance of as:
Then, following Equation 17 and the conditions in Equation 29, we conclude the proof of the upper bound on the conditional variance of :
where .
Finally, it only remains to prove that the event occurs with high probability for sufficiently large :
Lemma 3. The probability of occurrence of the event
is upper-bounded as follows:
for some constant satisfying the conditions of Equation (29).
Proof of Lemma 3.
First, using the union bound, we have:
Next, we bound the probabilities on the right hand side using Chernoff’s inequality (Boucheron et al., 2013). First, note that:
where follows if (which will hold under the conditions in Equation 29) and has been derived by applying the Chernoff’s bound on the Gaussian random variable . From the same reasoning, we see that . Combining these two results, we get the upper bound:
Next, note that:
where follows from the observation (which is a consequence of ). Then, we note that the zero-mean random variable is sub-Gaussian with variance factor . Thus, using the Chernoff’s inequality on sub-Gaussian random variables (Boucheron et al., 2013), we derive the upper-bound in Equation 52. In a similar fashion, based on the observation , we conclude the bound:
By combining the bounds in Equation 51, Equation 52, and Equation 53, the upper bound on in Equation 50 takes the form:
Finally, under the assumptions in Equation 29, we further simplify this bound as:
where we have used (which gives ) and to show that . Thus, ensures that , for . ■
This concludes the proof of Theorem 1.■
Appendix 3
Adapting the proposed signal and noise correlation estimates to spiking observations
While Algorithm 1 takes two-photon fluorescence observations as input and produces estimates of signal and noise correlation as output, it is possible to adapt it to spiking observations obtained by electrophysiology recordings. The resulting algorithm is obtained by simplifying the variational inference procedure in Algorithm 1 and is given below for completeness:
| Algorithm 2 Estimation of and from spiking observations |
|---|
| Inputs: Ensemble of spiking observations , constant , hyper-parameters and , tolerance at convergence δ and the external stimulus Outputs: and Initialization: Initial choice of , , and , , 1. while do Update variational parameters 2. for and do 3. 4. 5. for do 6. 7. 8. end for 9. end for 10. Update outputs and the convergence criterion 11. for do 12. 13. end for 14. , 15. , 16. 17. end while 18. Return and |
Data availability
A MATLAB implementation of the proposed method has been archived in Github at https://github.com/Anuththara-Rupasinghe/Signal-Noise-Correlation (copy archived at https://archive.softwareheritage.org/swh:1:rev:7397cc8d751a128f41df81f8af160014b22974d6). The data used in this work have been deposited in the Digital Repository at the University of Maryland at http://hdl.handle.net/1903/26917.
-
Digital Repository at the University of MarylandID 1903/26917. Experimental Data from `Direct Extraction of Signal and Noise Correlations from Two-Photon Calcium Imaging of Ensemble Neuronal Activity'.
References
-
ConferenceModel-based bayesian inference of neural activity and connectivity from all-optical interrogation of a neural circuitAdvances in Neural Information Processing Systems. pp. 3486–3495.
-
A survey of cross-validation procedures for model selectionStatistics Surveys 4:40–79.https://doi.org/10.1214/09-SS054
-
Neural correlations, population coding and computationNature Reviews Neuroscience 7:358–366.https://doi.org/10.1038/nrn1888
-
Convergence and stability of iteratively Re-weighted least squares algorithmsIEEE Transactions on Signal Processing 62:183–195.https://doi.org/10.1109/TSP.2013.2287685
-
Information-Limiting correlations in large neural populationsThe Journal of Neuroscience 40:1668–1678.https://doi.org/10.1523/JNEUROSCI.2072-19.2019
-
ThesisVariational algorithms for approximate Bayesian inference, PhD thesisUniversity of London, University College London (United Kingdom).
-
BookPattern Recognition and Machine Learning (Information Science and StatisticsBerlin, Heidelberg: Springer-Verlag.
-
Variational inference: a review for statisticiansJournal of the American Statistical Association 112:859–877.https://doi.org/10.1080/01621459.2017.1285773
-
BookConcentration Inequalities: A Nonasymptotic Theory of IndependenceOUP Oxford Press.
-
Neuronal avalanches in input and associative layers of auditory cortexFrontiers in Systems Neuroscience 13:45.https://doi.org/10.3389/fnsys.2019.00045
-
Measuring and interpreting neuronal correlationsNature Neuroscience 14:811–819.https://doi.org/10.1038/nn.2842
-
Attention improves performance primarily by reducing interneuronal correlationsNature Neuroscience 12:1594–1600.https://doi.org/10.1038/nn.2439
-
Binary spiking in auditory cortexThe Journal of Neuroscience 23:7940–7949.https://doi.org/10.1523/JNEUROSCI.23-21-07940.2003
-
Model selection techniques: an overviewIEEE Signal Processing Magazine 35:16–34.https://doi.org/10.1109/MSP.2018.2867638
-
Dynamic analysis of neural encoding by point process adaptive filteringNeural Computation 16:971–998.https://doi.org/10.1162/089976604773135069
-
Hierarchy of neural organization in the embryonic spinal cord: granger-causality graph analysis of in vivo calcium imaging dataIEEE Transactions on Neural Systems and Rehabilitation Engineering 23:333–341.https://doi.org/10.1109/TNSRE.2014.2341632
-
Fast online deconvolution of calcium imaging dataPLOS Computational Biology 13:e1005423.https://doi.org/10.1371/journal.pcbi.1005423
-
How independent are the messages carried by adjacent inferior temporal cortical neurons?The Journal of Neuroscience 13:2758–2771.https://doi.org/10.1523/JNEUROSCI.13-07-02758.1993
-
Fast nonconvex deconvolution of calcium imaging dataBiostatistics 21:709–726.https://doi.org/10.1093/biostatistics/kxy083
-
Exact spike train inference via $\ell_{0}$ optimizationThe Annals of Applied Statistics 12:2457–2482.https://doi.org/10.1214/18-AOAS1162
-
An introduction to variational methods for graphical modelsMachine Learning 37:183–233.https://doi.org/10.1023/A:1007665907178
-
Stimulus-dependent correlations and population codesNeural Computation 21:2774–2804.https://doi.org/10.1162/neco.2009.10-08-879
-
Fast and stable signal deconvolution via compressible State-Space modelsIEEE Transactions on Biomedical Engineering 65:74–86.https://doi.org/10.1109/TBME.2017.2694339
-
BookIdentifying signal and noise structure in neural population activity with Gaussian process factor modelsIn: Larochelle H, Ranzato M, Hadsell R, Balcan M. F, Lin H, editors. Advances in Neural Information Processing Systems. Curran Associates, Inc. pp. 1–84.https://doi.org/10.1101/2020.07.23.217984
-
Correlations and neuronal population informationAnnual Review of Neuroscience 39:237–256.https://doi.org/10.1146/annurev-neuro-070815-013851
-
Stimulus dependence of neuronal correlation in primary visual cortex of the macaqueJournal of Neuroscience 25:3661–3673.https://doi.org/10.1523/JNEUROSCI.5106-04.2005
-
Spectrotemporal structure of receptive fields in Areas AI and AAF of mouse auditory cortexJournal of Neurophysiology 90:2660–2675.https://doi.org/10.1152/jn.00751.2002
-
ConferenceBayesian latent structure discovery from multi-neuron recordingsAdvances in Neural Information Processing Systems. pp. 2002–2010.
-
A proof of the triangle inequality for the tanimoto distanceJournal of Mathematical Chemistry 26:263–265.https://doi.org/10.1023/A:1019154432472
-
Inference of neuronal network spike dynamics and topology from calcium imaging dataFrontiers in Neural Circuits 7:201.https://doi.org/10.3389/fncir.2013.00201
-
Nonlinear transfer of signal and noise correlations in cortical networksJournal of Neuroscience 35:8065–8080.https://doi.org/10.1523/JNEUROSCI.4738-14.2015
-
Sublaminar subdivision of mouse auditory cortex layer 2/3 based on functional translaminar connectionsThe Journal of Neuroscience 37:10200–10214.https://doi.org/10.1523/JNEUROSCI.1361-17.2017
-
A bayesian approach for inferring neuronal connectivity from calcium fluorescent imaging dataThe Annals of Applied Statistics 5:1229–1261.https://doi.org/10.1214/09-AOAS303
-
Population coding in mouse visual cortex: response reliability and dissociability of stimulus tuning and noise correlationFrontiers in Computational Neuroscience 8:58.https://doi.org/10.3389/fncom.2014.00058
-
Robustness of spike deconvolution for neuronal calcium imagingThe Journal of Neuroscience 38:7976–7985.https://doi.org/10.1523/JNEUROSCI.3339-17.2018
-
Maximum likelihood estimation of cascade point-process neural encoding modelsNetwork: Computation in Neural Systems 15:243–262.https://doi.org/10.1088/0954-898X_15_4_002
-
BookFully Bayesian inference for neural models with negative-binomial spikingIn: Pereira F, Burges C. J. C, Bottou L, Weinberger K. Q, editors. Advances in Neural Information Processing Systems. Curran Associates, Inc. pp. 1898–1906.
-
Bayesian inference for logistic models using Pólya–Gamma Latent VariablesJournal of the American Statistical Association 108:1339–1349.https://doi.org/10.1080/01621459.2013.829001
-
Maximum likelihood estimates of linear dynamic systemsAIAA Journal 3:1445–1450.https://doi.org/10.2514/3.3166
-
An integrated calcium imaging processing toolbox for the analysis of neuronal population dynamicsPLOS Computational Biology 13:e1005526.https://doi.org/10.1371/journal.pcbi.1005526
-
Functional organization and population dynamics in the mouse primary auditory cortexNature Neuroscience 13:353–360.https://doi.org/10.1038/nn.2484
-
ReportExperimental Data From ‘Direct Extraction of Signal and Noise Correlations From Two-Photon Calcium Imaging of Ensemble Neuronal Activity’Digital Repository at the University of Maryland (DRUM).
-
ConferenceRobust inference of neuronal correlations from blurred and noisy spiking observations2020 54th Annual Conference on Information Sciences and Systems (CISS). pp. 1–5.https://doi.org/10.1109/CISS48834.2020.1570617409
-
An approach to time series smoothing and forecasting using the em algorithmJournal of Time Series Analysis 3:253–264.https://doi.org/10.1111/j.1467-9892.1982.tb00349.x
-
Estimating a state-space model from point process observationsNeural Computation 15:965–991.https://doi.org/10.1162/089976603765202622
-
Spatial and temporal scales of neuronal correlation in visual area V4Journal of Neuroscience 33:5422–5432.https://doi.org/10.1523/JNEUROSCI.4782-12.2013
-
Population coding in neuronal systems with correlated noisePhysical Review E 64:051904.https://doi.org/10.1103/PhysRevE.64.051904
-
Efficient "Shotgun" Inference of Neural Connectivity from Highly Sub-sampled Activity DataPLOS Computational Biology 11:e1004464.https://doi.org/10.1371/journal.pcbi.1004464
-
Computational processing of neural recordings from calcium imaging dataCurrent Opinion in Neurobiology 55:22–31.https://doi.org/10.1016/j.conb.2018.11.005
-
Separating spike count correlation from firing rate correlationNeural Computation 28:849–881.https://doi.org/10.1162/NECO_a_00831
-
Spike inference from calcium imaging using sequential monte carlo methodsBiophysical Journal 97:636–655.https://doi.org/10.1016/j.bpj.2008.08.005
-
Fast nonnegative deconvolution for spike train inference from population calcium imagingJournal of Neurophysiology 104:3691–3704.https://doi.org/10.1152/jn.01073.2009
-
Variational inference in nonconjugate modelsJournal of Machine Learning Research : JMLR 14:1005–1031.https://doi.org/10.5555/2567709.2502613
-
Spatial pattern of intra-laminar connectivity in supragranular mouse auditory cortexFrontiers in Neural Circuits 8:15.https://doi.org/10.3389/fncir.2014.00015
-
Laminar transformation of frequency organization in auditory cortexJournal of Neuroscience 33:1498–1508.https://doi.org/10.1523/JNEUROSCI.3101-12.2013
-
Asymptotic approximations of integralsSociety for Industrial and Applied Mathematics 1:260.https://doi.org/10.1137/1.9780898719260
-
Improved estimation and interpretation of correlations in neural circuitsPLOS Computational Biology 11:e1004083.https://doi.org/10.1371/journal.pcbi.1004083
-
Gaussian-Process factor analysis for Low-Dimensional Single-Trial analysis of neural population activityJournal of Neurophysiology 102:614–635.https://doi.org/10.1152/jn.90941.2008
-
Higher-order interactions characterized in cortical activityJournal of Neuroscience 31:17514–17526.https://doi.org/10.1523/JNEUROSCI.3127-11.2011
Article and author information
Author details
Funding
National Science Foundation (1807216)
- Behtash Babadi
National Science Foundation (2032649)
- Behtash Babadi
National Institutes of Health (1U19NS107464)
- Patrick O Kanold
- Behtash Babadi
The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.
Acknowledgements
The authors thank Daniel E Winkowski for collecting the data in Bowen et al., 2019 that was also used in this work.
Ethics
Animal experimentation: All procedures, under Kanold lab protocol R-JAN-19-06, conformed to the guidelines of the University of Maryland Institutional Animal Care and Use Committee and the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health.
Copyright
© 2021, Rupasinghe et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.
Metrics
-
- 4,058
- views
-
- 477
- downloads
-
- 25
- citations
Views, downloads and citations are aggregated across all versions of this paper published by eLife.
Citations by DOI
-
- 25
- citations for umbrella DOI https://doi.org/10.7554/eLife.68046






