Quantifying concordant genetic effects of de novo mutations on multiple disorders
- Center for Statistical Science, Tsinghua University, China
- Department of Industrial Engineering, Tsinghua University, China
- MOE Key Laboratory of Bioinformatics, School of Life Sciences, Tsinghua University, China
- Yale School of Management, Yale University, United States
- Department of Genetics, Washington University in St. Louis, United States
- Department of Genetics, Yale University, United States
- Laboratory of Human Genetics and Genomics, Rockefeller University, United States
- Department of Biostatistics, Yale School of Public Health, United States
- Department of Pediatrics, Yale University, United States
- Program of Computational Biology and Bioinformatics, Yale University, United States
- Department of Biostatistics and Medical Informatics, University of Wisconsin-Madison, United States
Figures
Figure 1
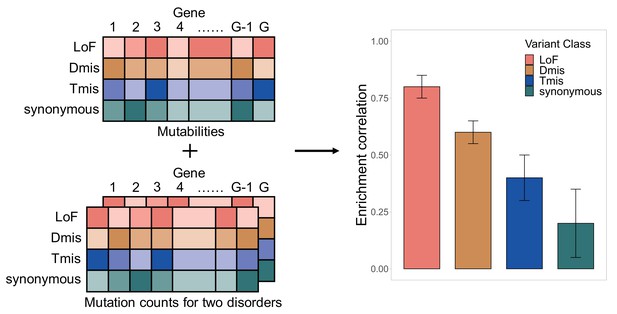
EncoreDNM workflow.
The inputs of EncoreDNM are de novo mutability of each gene and exome-wide, annotated DNM counts from two studies. We fit a mixed-effects Poisson model to estimate the DNM enrichment correlation between two disorders for each variant class.
Figure 2 with 2 supplements
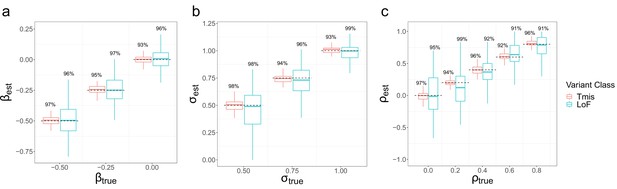
Parameter estimation results of EncoreDNM.
(a) Boxplot of estimates in single-trait analysis with fixed at 0.75. (b) Boxplot of estimates in single-trait analysis with fixed at –0.25. (c) Boxplot of estimates in cross-trait analysis with and fixed at –0.25 and 0.75. True parameter values are marked by dashed lines. The number above each box represents the coverage rate of 95% Wald confidence intervals. Each simulation setting was repeated 100 times.
Figure 2—figure supplement 1
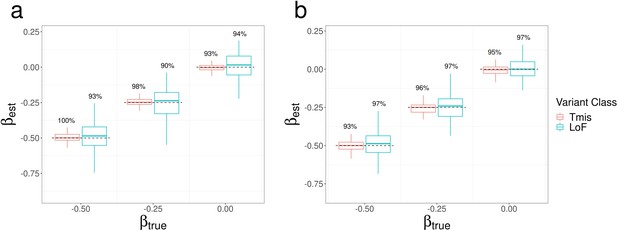
Estimation results of elevation parameter under a mixed-effects Poisson regression model.
Boxplots of estimated value for in single trait analysis with value fixed at (a) 0.5 and (b) 1. True parameter values are marked by dashed lines. The number above each box represents the coverage rate of 95% Wald confidence intervals. Each simulation setting was repeated 100 times.
Figure 2—figure supplement 2
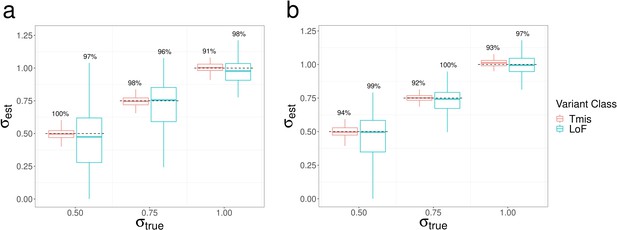
Estimation results of dispersion parameter under a mixed-effects Poisson regression model.
Boxplots of estimated value for in single trait analysis with value fixed at (a) –0.5 and (b) 0. True parameter values are marked by dashed lines. The number above each box represents the coverage rate of 95% Wald confidence intervals. Each simulation setting was repeated 100 times.
Figure 3
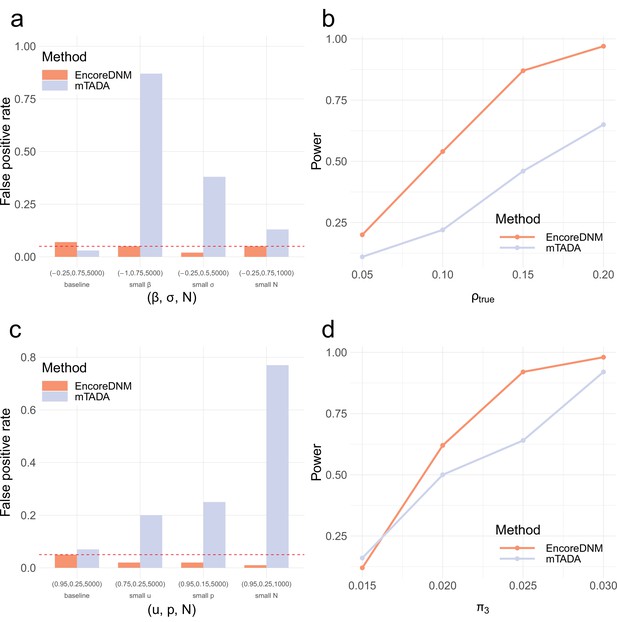
Comparison of EncoreDNM and mTADA.
(a) False positive rates under a mixed-effects Poisson regression model. (b) Statistical power of two methods under a mixed-effects Poisson regression model as the enrichment correlation increases. Parameters () were fixed at (–0.25, 0.75, 5000) for both disorders. (c) False positive rates under a multinomial model. (d) Statistical power under a multinomial model with varying proportion of shared causal genes. Parameters () were fixed at (0.95, 0.25, 5000) for both disorders. Each simulation setting was repeated 100 times.
Figure 4 with 1 supplement
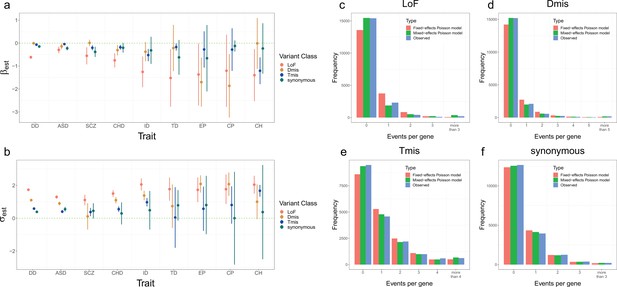
Model fitting results for nine disorders.
(a, b) Estimation results of and for nine disorders and four variant classes. Error bars represent 1.96*standard errors. Sample sizes of DNM datasets for each disorder are provided in Supplementary file 1-STable 1. (c–f) Distribution of DNM events per gene in four variant classes for developmental disorder. Red and green bars represent the expected frequency of genes under the fixed-effects and mixed-effects Poisson regression models, respectively. Blue bars represent the observed frequency of genes.
Figure 4—figure supplement 1
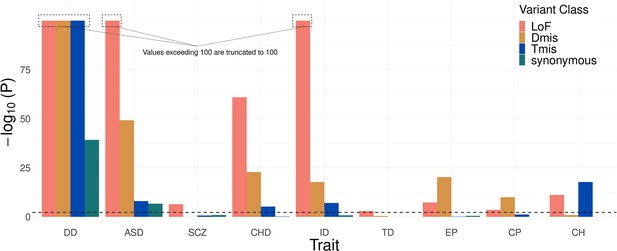
Likelihood ratio test shows significantly improved goodness of fit of the mixed-effects Poisson model compared to a fixed-effects model without the deviation component.
Results with are truncated to 100 for visualization purpose.
Figure 5 with 9 supplements
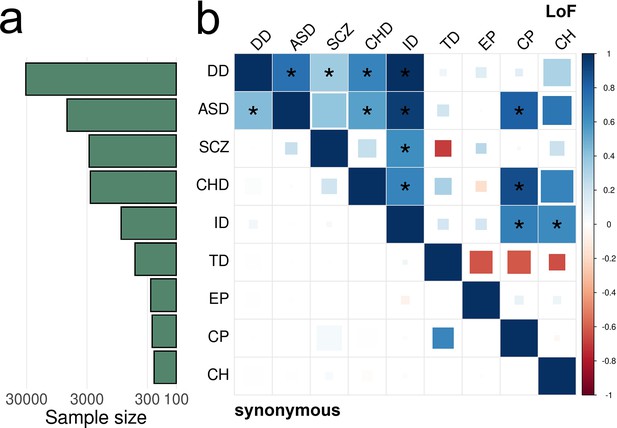
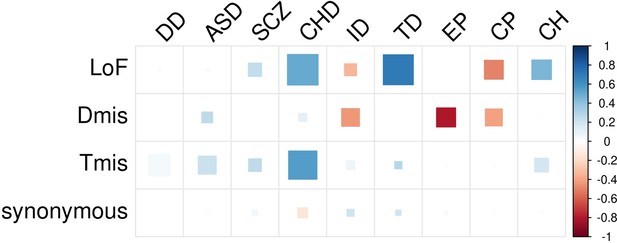
EncoreDNM identifies pervasive enrichment correlations of damaging DNMs among nine disorders.
(a) Shows sample size (for example, number of trios) for each disease. X-axis denotes sample size on the log scale. (b) Heatmap of enrichment correlations for LoF (upper triangle) and synonymous (lower triangle) DNMs among nine disorders. Larger squares represent more significant p-values, and deeper color represents stronger correlations. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 5—figure supplement 1
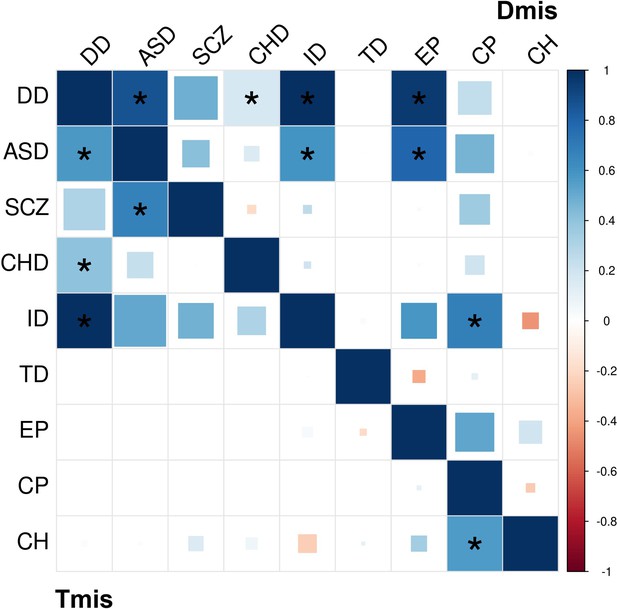
DNM enrichment correlations of nine disorders based on Dmis and Tmis variants.
Significant correlations (FDR <0.05) are marked by asterisks. Results with are truncated to 13 for visualization purpose.
Figure 5—figure supplement 2
DNM enrichment correlations between nine disorders and controls.
Figure 5—figure supplement 3
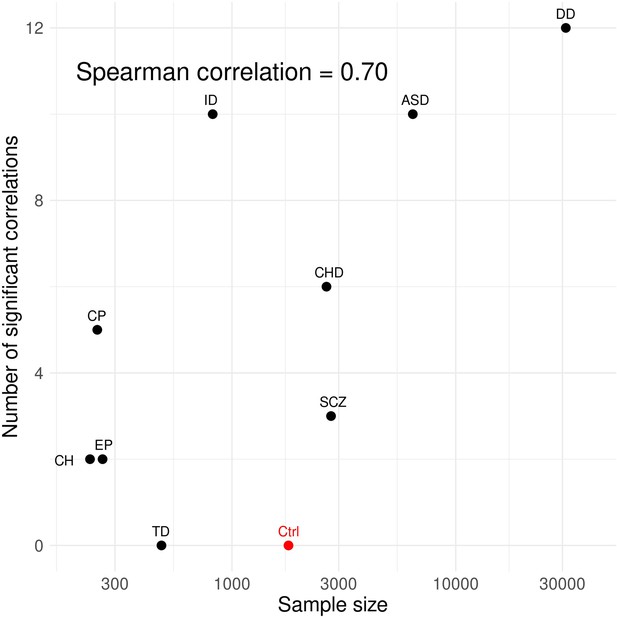
Number of significant correlations identified for each disorder is proportional to its sample size.
X-axis denotes number of trios in each study and is visualized in the log-scale. The data point for controls is a notable outlier and is excluded in the calculation of spearman correlation.
Figure 5—figure supplement 4
Lollipop plot for LoF DNMs in CTNNB1.
Red arrows highlight the DNMs in CP, ID, ASD, and CHD. Other DNMs are from DD probands.
Figure 5—figure supplement 5
Lollipop plot for LoF DNMs in FBXO11.
The red arrow highlights the two identical DNMs in ASD and CH. Other DNMs are from DD probands.
Figure 5—figure supplement 6
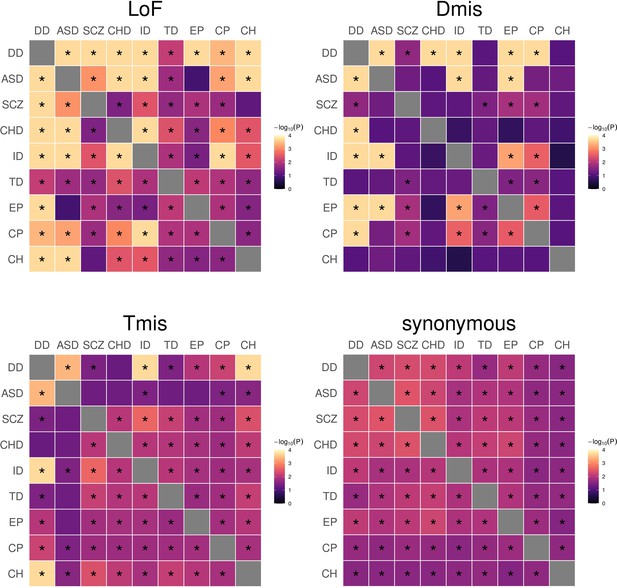
DNM genetic sharing in nine disorders estimated for LoF, Dmis, Tmis, and synonymous DNMs using mTADA.
Significant genetic sharings (FDR <0.05) are marked by asterisks.
Figure 5—figure supplement 7
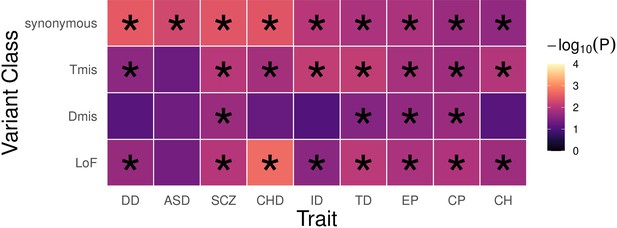
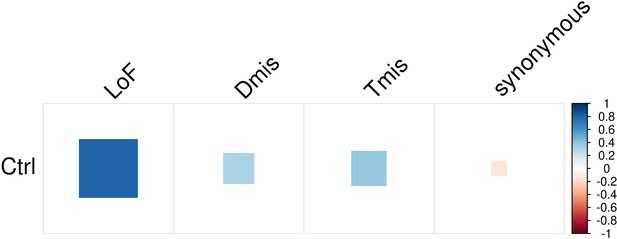
DNM genetic sharing in nine disorders and controls identified by mTADA.
Significant genetic sharings (FDR <0.05) are marked by asterisks.
Figure 5—figure supplement 8
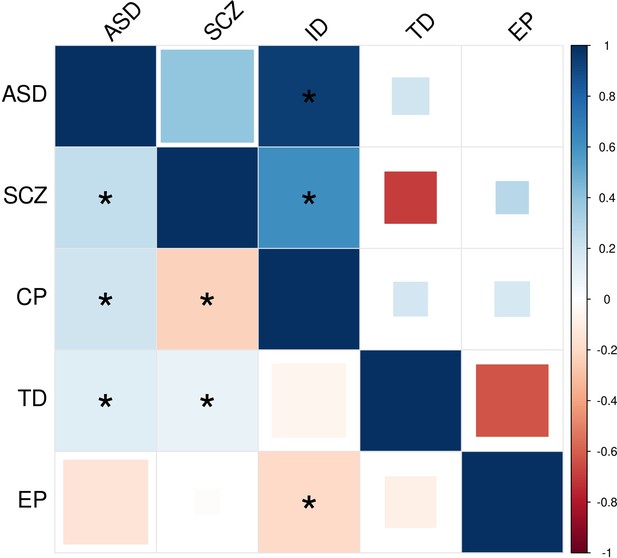
Comparison of GWAS- and DNM-based estimation of genetic sharing among five disorders.
The upper triangle represents enrichment correlations estimated by EncoreDNM. The lower triangle represents genetic correlations estimated from GWAS summary statistics by cross-trait LDSC. We used GWAS on cognitive performance as a proxy for ID. Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 5—figure supplement 9
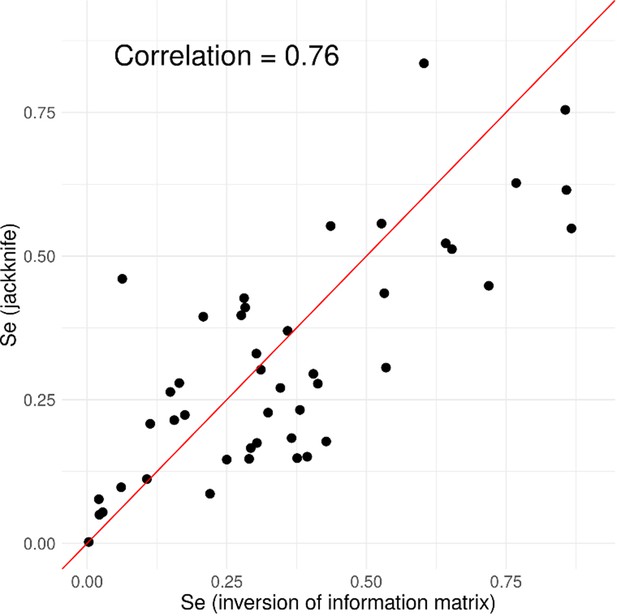
Group-wise jackknife method and inversion of Fisher information matrix method produced similar standard error estimates for LoF variants.
Figure 6 with 8 supplements
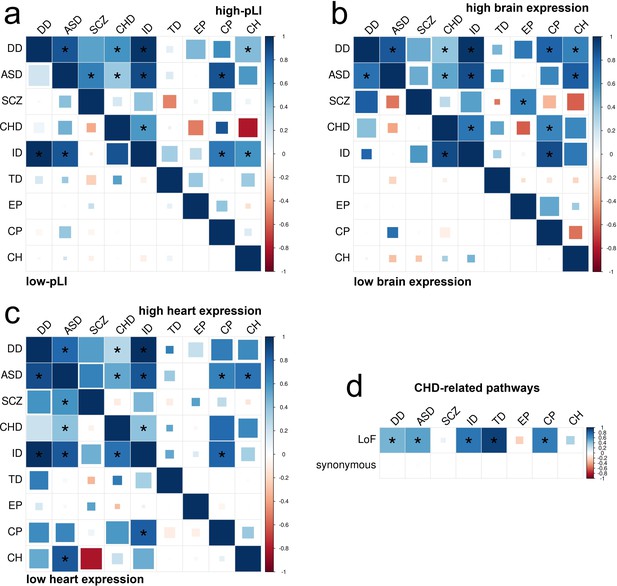
DNM enrichment correlations in disease-relevant gene sets.
(a) Enrichment correlations in high-pLI genes (upper triangle) and low-pLI genes (lower triangle) for LoF variants. Here, pLI is the probability of being loss-of-function intolerant (see Materials and methods). (b) Enrichment correlations in HBE genes (upper triangle) and LBE genes (lower triangle) for LoF variants. (c) Enrichment correlations in HHE genes (upper triangle) and LHE genes (lower triangle) for LoF variants. (d) Enrichment correlations in CHD-related pathways for LoF and synonymous variants. Larger squares represent more significant p-values, and deeper color represents stronger correlations. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 1
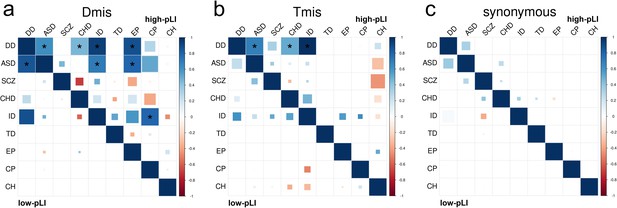
DNM enrichment correlations in high-pLI genes (upper triangle) and low-pLI genes (lower triangle) for Dmis, Tmis, and synonymous variants.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 2
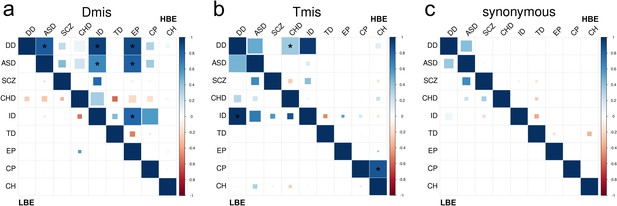
DNM enrichment correlations in HBE genes (upper triangle) and LBE genes (lower triangle) for Dmis, Tmis, and synonymous variants.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 3
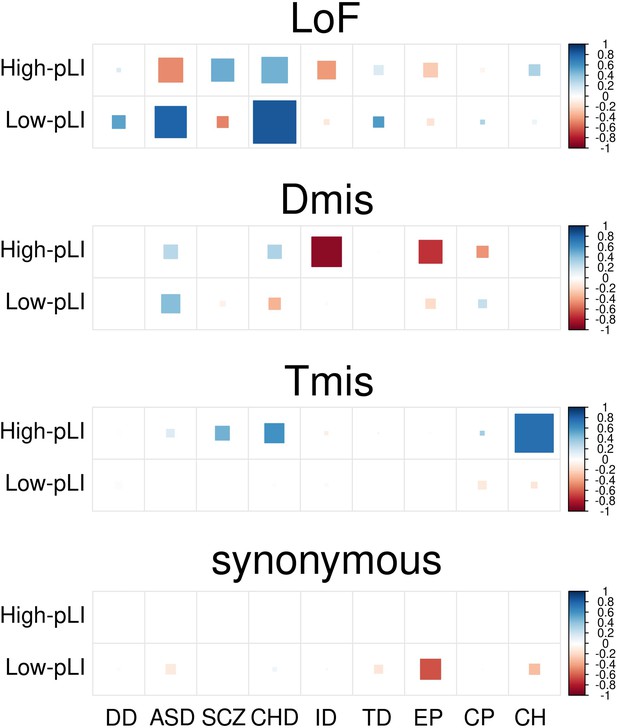
DNM enrichment correlations between nine disorders and controls in high-pLI and low-pLI gene sets.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 4
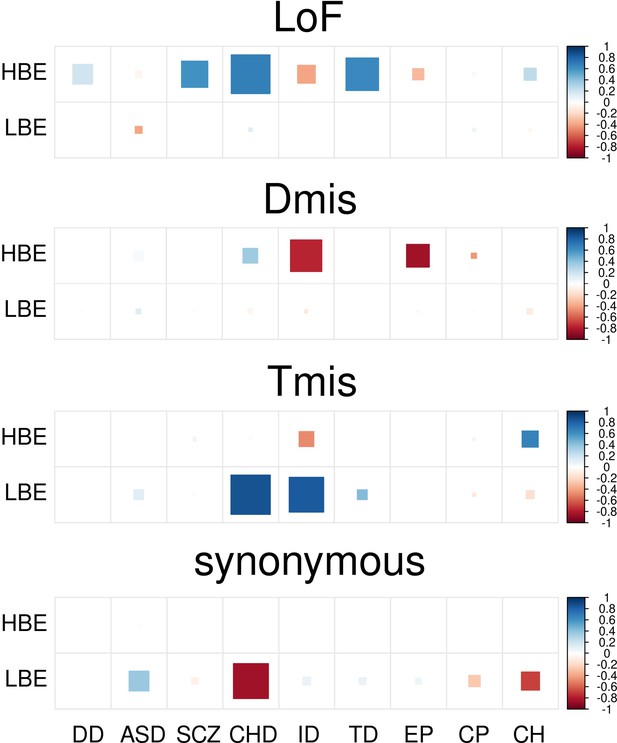
DNM enrichment correlations between nine disorders and controls in HBE and LBE genes.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 5
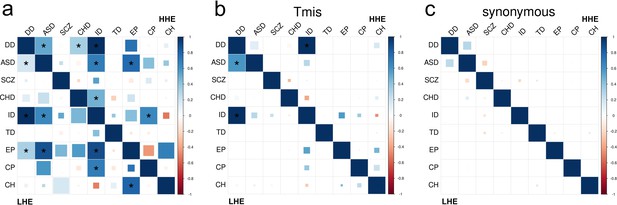
DNM enrichment correlations in HHE genes (upper triangle) and LHE genes (lower triangle) for Dmis, Tmis, and synonymous variants.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 6
DNM enrichment correlations in CHD-related pathways for Dmis and Tmis variants.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 7
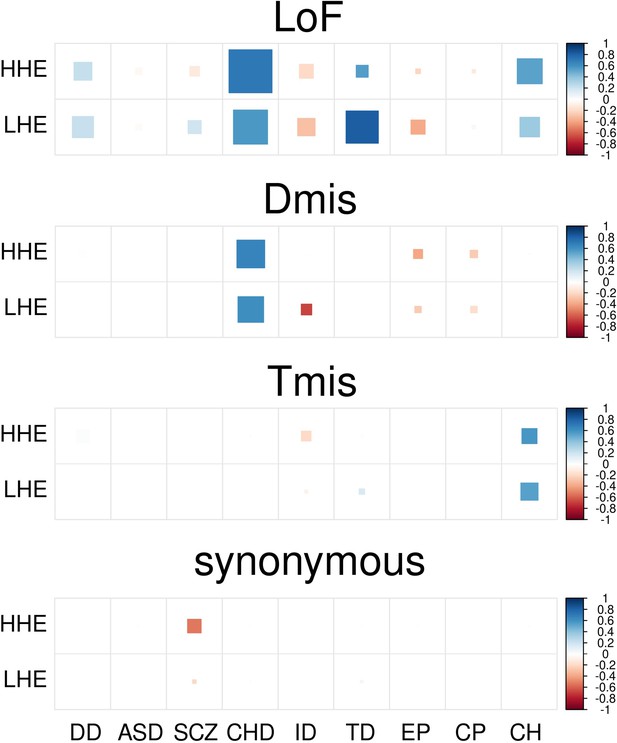
DNM enrichment correlations between nine disorders and controls in HHE and LHE gene sets.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Figure 6—figure supplement 8
DNM enrichment correlations between CHD and controls in CHD-related pathways.
Larger square represents more significant p-value, and deeper color represents stronger correlation. Significant correlations (FDR <0.05) are shown as full-sized squares marked by asterisks.
Additional files
-
Supplementary file 1
Supplementary Tables 1-20.
- https://cdn.elifesciences.org/articles/75551/elife-75551-supp1-v2.xlsx
-
MDAR checklist
- https://cdn.elifesciences.org/articles/75551/elife-75551-mdarchecklist1-v2.pdf
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Quantifying concordant genetic effects of de novo mutations on multiple disorders
eLife 11:e75551.
https://doi.org/10.7554/eLife.75551
