Figures and data in Uncertainty-modulated prediction errors in cortical microcircuits

Figures
Tables
Additional files

9 figures, 6 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

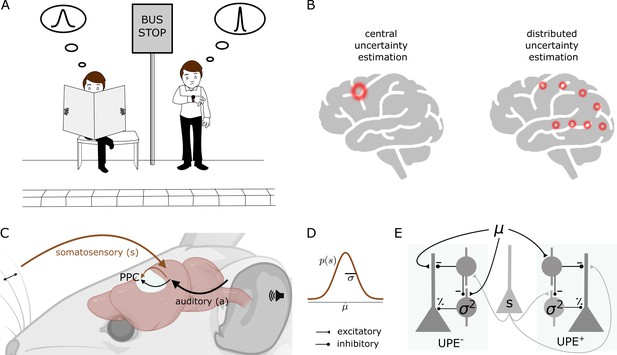
Distributed uncertainty-modulated prediction error computation in cortical circuits.

(A) A person who learned that buses are unreliable has a prior expectation, which can be described by a wide Gaussian distribution of expected bus arrival times. When the bus does not arrive at the scheduled time, this person is not surprised and remains calm, as everything happens according to their model of the world. On the other hand, a person who learned that buses are punctual, which can be described by a narrow distribution of arrival times, may notice that the bus is late and get nervous, as they expected the bus to be punctual. This person can learn from this experience. If they always took this particular bus, and their uncertainty estimate is accurate, the prediction error could indicate that the bus schedule changed. (B) Models of uncertainty representation in cortex. Some models suggest that uncertainty is only represented in higher level areas concerned with decision-making (left). In contrast, we propose that uncertainty is represented at each level of the cortical hierarchy (right, shown is the visual hierarchy as an example). (C) A mouse learns the association between a sound ( $a$ ) and a whisker deflection ( $s$ ). The posterior parietal cortex (PPC) receives inputs from both somatosensory and auditory cortex. (D) The whisker stimulus intensities are drawn from a Gaussian distribution with mean μ and standard deviation $σ$ . (E) Negative (left) and positive (right) prediction error circuit consisting of three cell types: layer 2/3 pyramidal cells (triangle), somatostatin-positive interneurons (SST, circle) and parvalbumin-positive interneurons (PV). SSTs represent the mean prediction in the postive circuit and the stimulus in the negative circuit, and PVs represent the variance.

Figure 2

Download asset Open asset

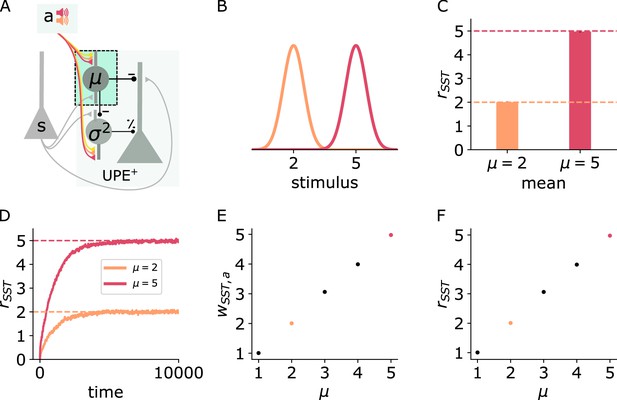
SSTs learn to represent the mean context-dependently.

Illustration of the changes in the positive prediction error circuit. Thicker lines denote stronger weights. (B) Two different tones (red, orange) are associated with two somatosensory stimulus distributions with different means (red: high, orange: low). (C) SST firing rates (mean and std) during stimulus input. (D) SST firing rates over time for low (orange) and high (red) stimulus means. (E) Weights (mean and std) from sound a to SST for different values of μ. (F) SST firing rates (mean and std) for different values of μ. Mean and std were computed over 1000 data points from timestep 9000–10,000.

Figure 3 with 3 supplements

Download asset Open asset

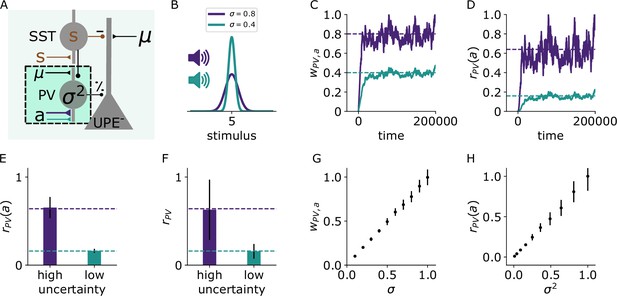
PVs learn to estimate the variance context-dependently.

(A) Illustration of the changes in the positive prediction error circuit. Thicker lines denote stronger weights. (B) Two different tones (purple, green) are associated with two somatosensory stimulus distributions with different variances (purple: high, green: low). (C) Weights from sound a to PV over time for two different values of stimulus variance (high: $σ = 0.8$ [purple], low: $σ = 0.4$ [green]). (D) PV firing rates over time given sound input (without whisker stimulus input) for low (green) and high (purple) stimulus variance. (E) PV firing rates (mean and std) given sound input and whisker stimuli for low and high stimulus variance. (F) PV firing rates (mean and std) during sound and stimulus input. (G) Weights (mean and std) from sound $a$ to PV for different values of $σ$ . (H) PV firing rates (mean and std) given sound input for different values of $σ^{2}$ . Mean and std were computed from 150,000 data points from timestep 450,000–600,000.

Figure 3—figure supplement 1

Download asset Open asset

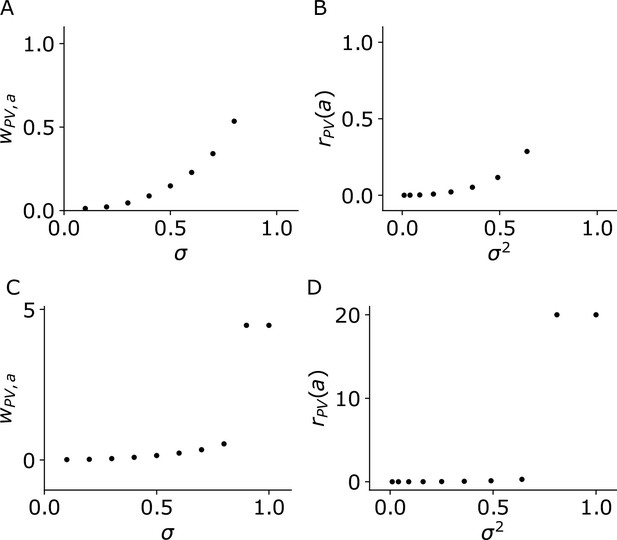
Different choice of supralinear activation function for PV.

Learning the variance in the positive prediction error circuit with PVs with a power activation function (exponent = 3.0). (**A, B**) are analogous to Figure 3G and H, and the circuit is the same except that the activation function of the PVs ( $ϕ_{P V} (x)$ ) has an exponent of 3.0 instead of 2.0. (**C, D**) are zoomed-out versions of (**A, B**).

Figure 3—figure supplement 2

Download asset Open asset

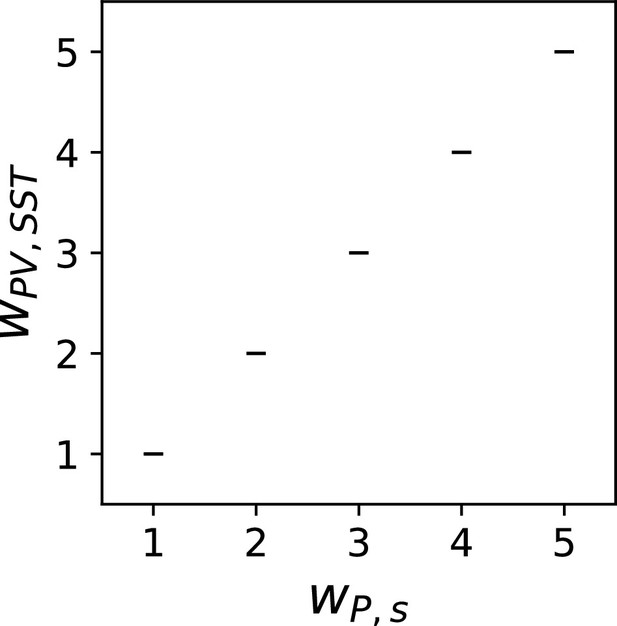
Plastic weights from SST to PV learn to match weights from $s$ to PV.

With inhibitory plasticity, weights from SST to PV can be learned. This figure shows that the weight from SST to PV ( $w_{P V, S S T}$ ) is equal to the weight from $s$ to PV ( $w_{PV, s}$ ). The inhibitory plasticity rule is described in the Appendix.

Figure 3—figure supplement 3

Download asset Open asset

PVs learn to represent the variance given an associative cue in the negative prediction error circuit.

(A) Illustration of the changes in the negative prediction error circuit. Thicker lines denote stronger weights. (B) Two different tones (purple, green) are associated with two somatosensory stimulus distributions with different variances (purple: high, green: low). (C) Weights from sound $a$ to PV over time for two different values of stimulus variance (high: $σ = 0.8$ [purple], low: $σ = 0.4$ [green]). (D) PV firing rates over time given sound input (without stimulus input) for low (green) and high (purple) stimulus variance. (E) PV firing rates (mean and std) given sound input for low and high stimulus variance. (F) PV firing rates (mean and std) during sound and stimulus input. (G) Weights from sound $a$ to PV for different values of $σ$ (mean and std). (H) PV firing rates given sound input for different values of $σ^{2}$ (mean and std).

Figure 4 with 1 supplement

Download asset Open asset

Calculation of the UPE in layer 2/3 error neurons.

(A) Illustration of the negative prediction error circuit. (B) Distributions with different standard deviations $σ$ . (C) Illustration of the positive prediction error circuit. (D) Firing rate of the error neuron in the negative prediction error circuit (UPE) as a function of $σ$ for two values of $| s - μ |$ after learning μ and $σ$ . (E) Rates of both UPE⁺ and UPE⁻-representing error neurons with a nonlinear activation function, where $k = 2.0$ , as a function of the difference between the stimulus and the mean ( $s - μ$ ). (F) Firing rate of the error neuron in the positive prediction error circuit (UPE⁺) as a function of $σ$ for two values of $| s - μ |$ after learning μ and $σ$ . (**G-I**) same as (**D-F**) for error neurons with $k = 2.5$ with the same legend as in (**D-F**).

Figure 4—figure supplement 1

Download asset Open asset

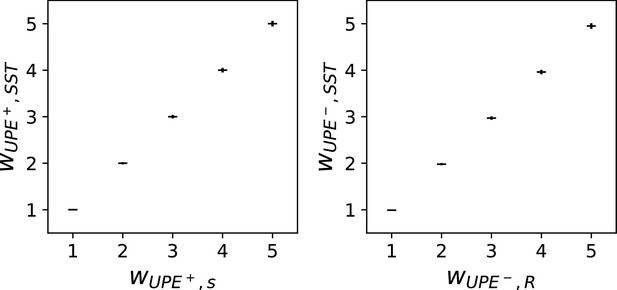
Learning the weights from the SSTs to the UPE neurons.

This figure shows that the weights from the SSTs to the UPEs in both the positive (left) and the negative (right) prediction error circuit can be learned with inhibitory plasticity to match the weights from the stimulus representation $s$ to the UPEs. The inhibitory plasticity rule is described in the Appendix.

Figure 5 with 1 supplement

Download asset Open asset

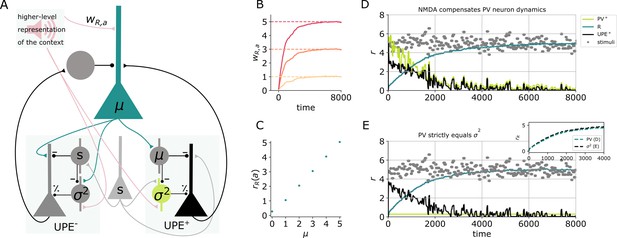
Learning the mean representation with UPEs.

(A) Illustration of the circuit. A representation neuron (turquoise) receives input from both positive and negative prediction error circuits (UPE⁺ and UPE⁻) and projects back to them. The UPE⁻ has a negative impact on the firing rate of the representation neuron ( $r_{R}$ ). A weight $w_{R, a}$ from the higher level representation of the context given by sound $a$ is learned. (B) Weights $w_{R, a}$ over time for different values of μ ( $μ \in [1, 3, 5]$ ). (C) R firing rates given sound input for different values of μ (mean and std over 50,000 data points from timestep 50,000–100,000,, the end of the simulation). (D) Activity of the different cell types (PV: light green, R: turquiose, UPE: black) and whisker stimulus samples (grey dots) over time. Learning the mean representation with PVs (light green) reflecting the MSE at the beginning, which is compensated by nonlinear activation of L2/3 neurons (black). The evolution of the mean rate of neuron $R$ (turquoise) is similar to the perfect case in (E). (E) Same colour code as in (D). Inset shows comparison to (D) Learning the mean representation assuming PVs (light green) perfectly represent the variance.

Figure 5—figure supplement 1

Download asset Open asset

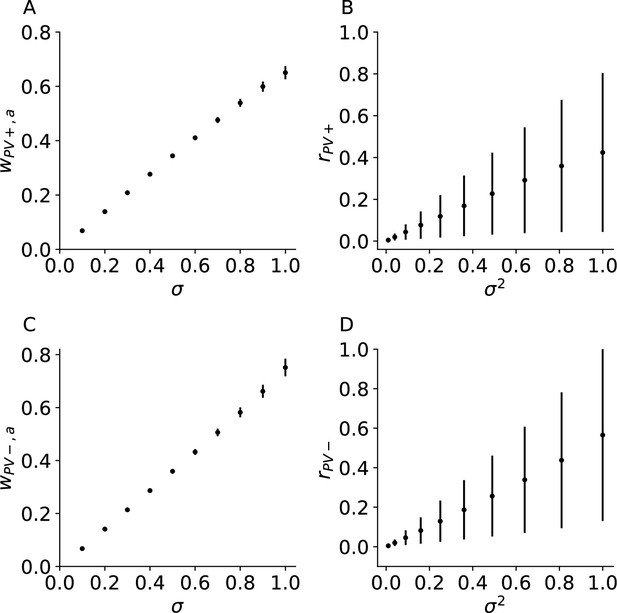
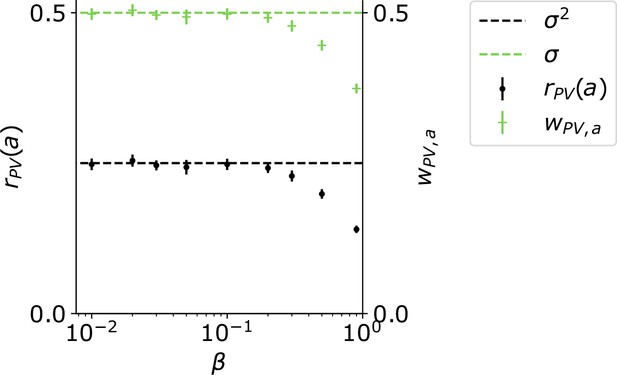
PV firing rates are proportional to the variance in the recurrent circuit model.

Weights from $a$ to PV as a function of $σ$ in the positive (A) and negative (C) prediction error subcircuit. PV firing rates as a function of $σ^{2}$ in the positive (B) and negative (D) prediction error circuit.

Figure 6

Download asset Open asset

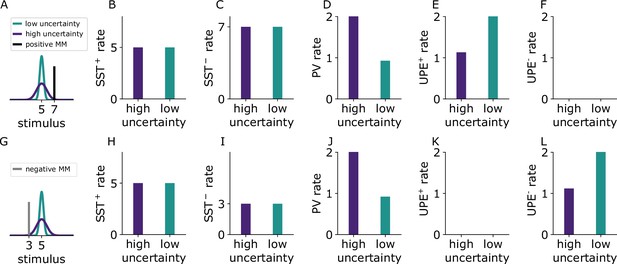
Cell-type-specific experimentally testable predictions.

(A) Illustration of the two experienced stimulus distributions with different variances that are associated with two different sounds (green, purple). The presented mismatch (MM) stimulus (black) is larger than expected (positive prediction error). (**B-F**) Simulated firing rates of different cell types to positive prediction errors when a sound associated with high (purple) or low (green) uncertainty is presented. (G) As in (A) the presented mismatch stimulus (grey) is smaller than expected (negative prediction error). (**H-L**) Firing rates of different cell types to the negative mismatch when a sound associated with high (purple) or low (green) uncertainty is presented. Because the firing rate predictions are equal for PV⁺ and PV⁻, we only show the results for PV⁺ in the figure.

Figure 7

Download asset Open asset

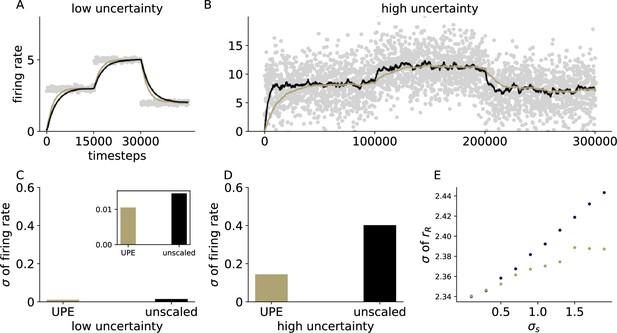
Effective learning rate is automatically adjusted with UPEs.

(**A, B**) Firing rate over time of the representation neuron in a circuit with uncertainty-modulated prediction errors (gold) and in a circuit with unmodulated errors (black) in a low uncertainty setting (A) and a high uncertainty setting (B). (C) Standard deviation of the firing rate of the representation neuron in the low uncertainty setting (inset has a different scale, outer axis scale matches the one in D). (D) Standard deviation of the firing rate of the representation neuron in the high uncertainty setting. (E) Standard deviation of the firing rate $r_{R}$ as a function of the standard deviation of the presented stimulus distribution $σ_{s}$ . Standard deviations were computed over 100,000 data points from timestep 100,000–200,000.

Figure 8

Download asset Open asset

UPEs ensure uncertainty-based weighting of prior and sensory information.

(A) Illustration of the hierarchical two-area model. A representation neuron ( $r$ ) in area $ℓ$ receives positive and negative UPEs from the area $ℓ - 1$ below (sensory prediction error, as in Figure 5), and positive and negative UPEs from the same area (representation prediction error) with different signs, see Equation 5. In this example, the uncertainty in area $ℓ - 1$ corresponds to the sensory uncertainty $σ_{s}^{2}$ , and the uncertainty in the area $ℓ$ above, corresponds to the prior uncertainty $σ_{p}^{2}$ . Both uncertainties are represented by PV activity in the respective area. (**B, C**) The simulation results from the hierarchical circuit model yield an uncertainty-based weighting of prior and sensory information as in Equation 4. (B) The activity $r$ of the representation neuron as a function of the stimulus $s$ for different amounts of prior uncertainty $σ_{p}^{2}$ , when the sensory uncertainty is fixed $σ_{s}^{2} = 0.5$ . The histograms show the distribution of the sensory stimulus samples (grey) and the distribution of the activity of the representation neuron (green). (C) The activity of the representation neuron as a function of the stimulus for different amounts of sensory uncertainty $σ_{s}^{2}$ , when the prior uncertainty is fixed $σ_{p}^{2} = 0.5$ .

Figure 9

Download asset Open asset

For small $β$ , and $w_{s} = \sqrt{\frac{2 - β}{β}}$ , the weight from $a$ to PV approaches $σ$ and the PV firing rate approaches $σ^{2}$ .

Tables

Table 1

Parameters of the network.

Parameter	Value	Description
$w_{{P V}^{+}, {S S T}^{+}}$	$\sqrt{\frac{2 - β}{β}}$	Weight from ${S S T}^{+}$ to ${P V}^{+}$
$w_{{P V}^{+}, s}$	$\sqrt{\frac{2 - β}{β}}$	Weight from $s$ to ${P V}^{+}$
$w_{{P V}^{-}, {S S T}^{-}}$	$\sqrt{\frac{2 - β}{β}}$	Weight from ${S S T}^{-}$ to ${P V}^{-}$
$w_{{P V}^{-}, R}$	$\sqrt{\frac{2 - β}{β}}$	Weight from $R$ to ${P V}^{-}$
$w_{{S S T}^{+}, R}$	1.0	Weight from $R$ to ${S S T}^{+}$
$w_{{S S T}^{-}, s}$	1.0	Weight from $s$ to ${SST}^{-}$
$w_{{U P E}^{+}, {S S T}^{+}}$	1.0	Weight from ${SST}^{+}$ to ${UPE}^{+}$
$w_{{U P E}^{+}, s}$	1.0	Weight from $s$ to ${UPE}^{+}$
$w_{{U P E}^{-}, R}$	1.0	Weight from $R$ to ${U P E}^{-}$
$w_{{U P E}^{-}, {S S T}^{-}}$	1.0	Weight from ${SST}^{-}$ to ${U P E}^{-}$
$w_{R, {U P E}^{+}}$	0.1(1.0)	Weight from ${U P E}^{+}$ to $R$ (Figure 6)
$w_{R, {U P E}^{-}}$	0.1(1.0)	Weight from ${UPE}^{-}$ to $R$ (Figure 6)
$x_{m a x}$	20	Limits neuronal activity
$β$	0.1	Nudging parameter

Table 2

Additional parameters of the hierarchical network.

Parameter	Value	Description
$w_{R, {U P E}_{ℓ}^{+}}$	1.0	Weight from ${UPE}_{ℓ}^{+}$ to $R$
$w_{R, {U P E}_{ℓ}^{-}}$	1.0	Weight from ${UPE}_{ℓ}^{-}$ to $R$
$w_{{U P E}_{ℓ}^{-}, R}$	1.0	Weight from $R$ to ${UPE}_{ℓ}^{-}$
$w_{{U P E}^{-}, p r i o r}$	1.0	Weight from $R$ to ${UPE}^{-}$

Table 3

Inputs.

Parameter	Value	Description
a	{0.0, 1.0}	Auditory stimulus (on/off)
$s$	$\sim N (μ, σ)$	Somatosensory (whisker) stimulus
$N$	1000–20,000	Number of whisker stimulus samples
$D$	{10, 100}	Stimulus duration (Figures 1—5 and 7)

Table 4

Parameters of the plasticity rules.

Parameter	Value	Description
$η_{S S T}$	0.1	Learning rate for $w_{{S S T}^{+ / -}, a}$
$η_{P V}$	$0.01 * η_{R} = 0.001$	Learning rate for $w_{{P V}^{+ / -}, a}$
$η_{R}$	0.1	Learning rate for $w_{R, a}$
$w_{S S T, a}^{i n i t i a l}$	0.01	Initial value for $w_{{S S T}^{+ / -}, a}$
$w_{P V, a}^{i n i t i a l}$	0.01	Initial value for $d t = 0.1$
$w_{R, a}^{i n i t i a l}$	0.01	Initial value for $w_{R, a}$

Table 5

Parameters of simulations in Figures 2—5.

Parameter	Value	Description
$T$	$N * D$	Simulation time
$d t$	0.1	Simulation time step
$τ_{E}$	1.0	Excitatory membrane time constant
$τ_{I}$	1.0	Inhibitory membrane time constant

Table 6

Parameters of the simulation in Figure 6.

Parameter	Value	Description
$T$	$N * D$	Simulation time
$d t$	0.1	Simulation time step
$τ_{E}$	10.0	Excitatory membrane time constant
$τ_{I}$	2.0	Inhibitory membrane time constant
$η_{R}$	0.01	Learning rate of $w_{R, A}$