Science Forum: Ten common statistical mistakes to watch out for when writing or reviewing a manuscript
- University College London, United Kingdom
- KU Leuven, Belgium
Figures
Figure 1
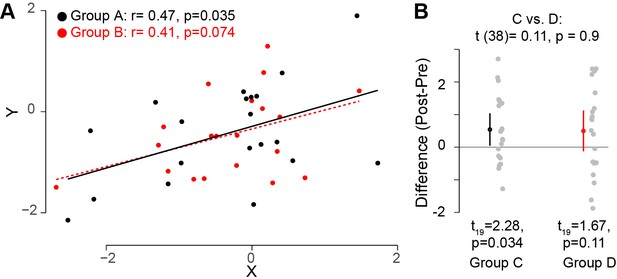
Interpreting comparisons between two effects without directly comparing them.
(A) Two variables, X and Y, were measured for two groups A and B. It looks clear that the correlation between these two variables does not differ across these two groups. However, if one compares both correlation coefficients to zero by calculating the significance of the Pearson's correlation coefficient r, it is possible to find that one group (group A; black circles; n = 20) has a statistically significant correlation (based on a threshold of p≤0.05), whereas the other group (group B, red circles; n = 20) does not. However, this does not indicate that the correlation between the variables X and Y differs between these groups. Monte Carlo simulations can be used to compare the correlations in the two groups (Wilcox and Tian, 2008). (B) In another experimental context, one can look at how a specific outcome measure (e.g. the difference pre- and post-training) differs between two groups. The means for groups C and D are the same, but the variance for group D is higher. If one uses a one-sample t-test to compare this outcome measure to zero for each group separately, it is possible to find that, this variable is significantly different from zero for one group (group C; left; n = 20), but not for the other group (group D, right; n = 20). However, this does not inform us whether this outcome measure is different between the two groups. Instead, one should directly compare the two groups by using an unpaired t-test (top): this shows that this outcome measure is not different for the two groups. Code (including the simulated data) available at github.com/jjodx/InferentialMistakes (Makin and Orban de Xivry, 2019; https://github.com/elifesciences-publications/InferentialMistakes).
Figure 2
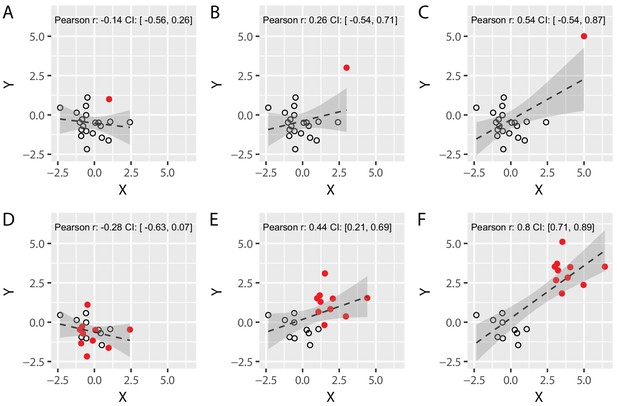
Spurious correlations: the effect of a single outlier and of subgroups on Pearson’s correlation coefficients.
(A–C) We simulated two different uncorrelated variables with 19 samples (black circles) and added an additional data point (solid red circle) whose distance from the main population was systematically varied until it became a formal outlier (panel C). Note that the value of Pearson’s correlation coefficient R artificially increases as the distance between the main population and the red data point is increased, demonstrating that a single data point can lead to spurious Pearson’s correlations. (D–F) We simulated two different uncorrelated variables with 20 sample that were arbitrarily divided into two subgroups (red vs. black, N = 10 each). We systematically varied the distance between the two subgroups from panel D to panel F. Again, the value of R artificially increases as the distance between the subgroups is increased. This shows that correlating variables without taking the existence of subgroups into account can yield spurious correlations. Confidence intervals (CI) are shown in grey, and were obtained via a bootstrap procedure (with the grey region representing the region between the 2.5 and 97.5 percentiles of the obtained distribution of correlation values). Code (including the simulated data) available at github.com/jjodx/InferentialMistakes.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Science Forum: Ten common statistical mistakes to watch out for when writing or reviewing a manuscript
eLife 8:e48175.
https://doi.org/10.7554/eLife.48175
