Strong inter-population cooperation leads to partner intermixing in microbial communities
- Fred Hutchinson Cancer Research Center, United States
- Montana State University, United States
Figures
Figure 1 with 3 supplements
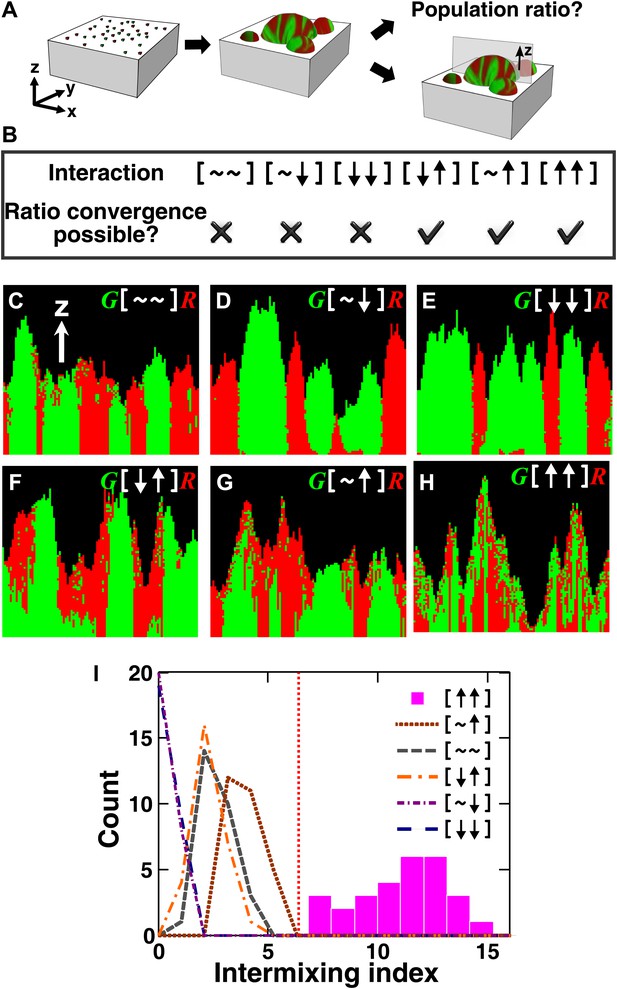
The fitness model generates two ecological patterning predictions.
(A) In all simulated and experimental communities (see ‘Materials and methods’), two populations of cells, marked in red and green, were initially randomly distributed on a surface unless otherwise …
-
Figure 1—source data 1
Parameter values used in the fitness model.
- https://doi.org/10.7554/eLife.00230.004
Figure 1—figure supplement 1
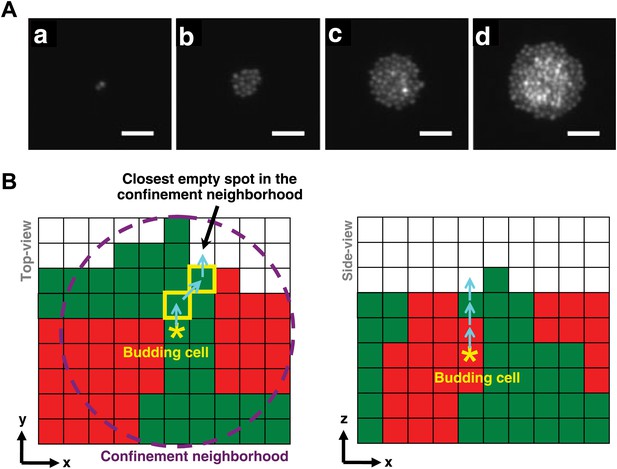
Cell rearrangement in simulations follows experimental observations on cells that are not actively motile.
(A) To incorporate realistic assumptions about cell rearrangement in three-dimensional communities, we monitored the growth of a single fluorescent yeast cell into a microcolony on top of solid …
Figure 1—figure supplement 2
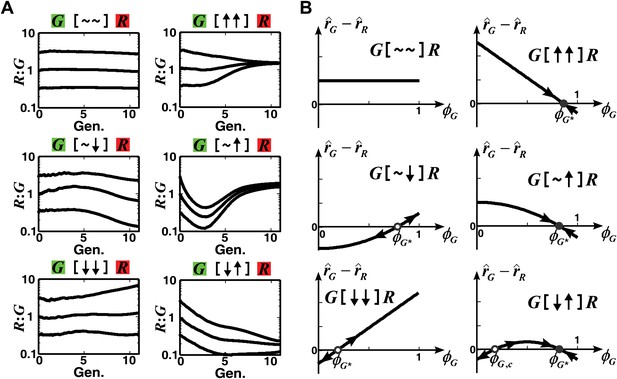
The fitness model predicts that convergence of population ratios is possible when an interaction benefits at least one partner.
(A) The fitness model demonstrated that interactions conferring large benefit to at least one partner could lead to ratio convergence. Simulation parameters are listed in Figure 1—source data 1. (B) …
Figure 1—figure supplement 3
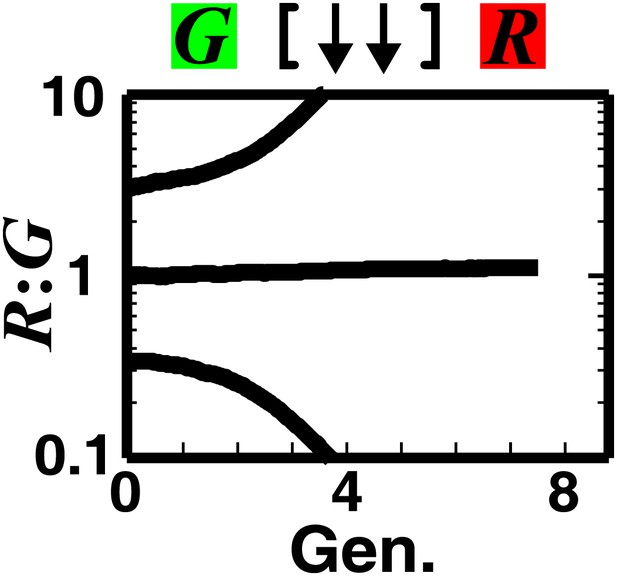
Strong mutual antagonism can lead to rapid divergence of population ratios.
The fitness model shows that if two partner populations inhibit each other sufficiently strongly compared to their basal fitness, population ratios may diverge rapidly.
Figure 2 with 4 supplements
Obligatory cooperation, but not competition or obligatory commensalism, results in substantial partner intermixing in engineered yeast communities and in communities simulated using the diffusion model.
Competitive communities of strains with equal fitness (equal-fitness competition, abbreviated as ‘Eq-fitness Comp.’) showed population segregation as suggested by static late-stage top-views (A, …
-
Figure 2—source data 1
Definitions and values of parameters used in the diffusion model.
- https://doi.org/10.7554/eLife.00230.010
Figure 2—figure supplement 1
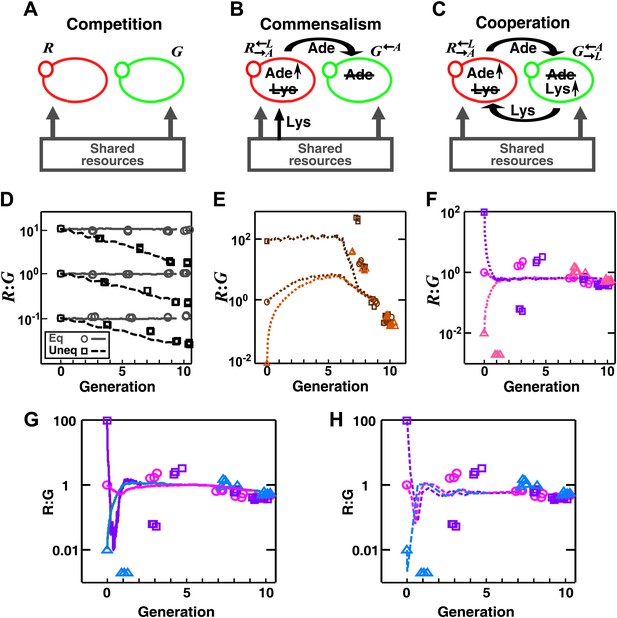
In engineered yeast communities, obligatory cooperation and obligatory commensalism allow initially different partner ratios to converge over time.
Engineered yeast communities consisted of two non-mating fluorescent strains of yeast, G and R, engaged in a metabolic interaction. (A) In competitive communities, two prototrophic strains engaged …
Figure 2—figure supplement 2
Basic assumptions in the diffusion model.
In the diffusion model, community grew on the top surface of an agarose column (light blue). Cell grids (black borders) represented cells at different states: live R (light red), live G (light …
Figure 2—figure supplement 3
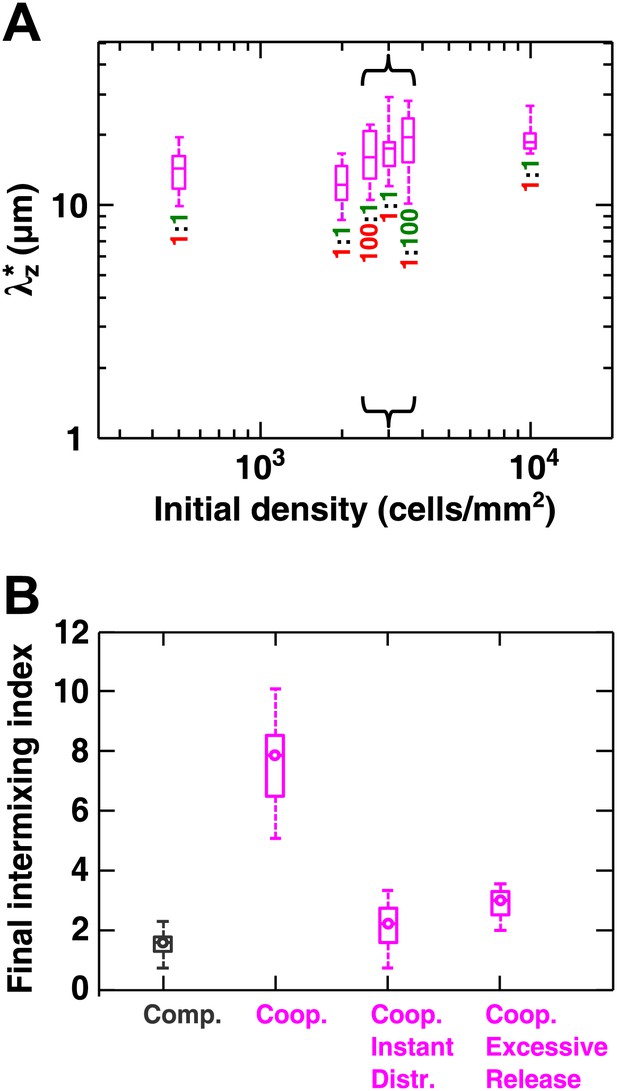
Cooperative communities exhibit a characteristic patch size associated with the spatial localization of benefits.
(A) Starting from densities and ratios spanning orders of magnitude, experimental obligatory cooperative yeast communities developed a consistent characteristic vertical patch size of ∼10 to 20 …
Figure 2—figure supplement 4
Obligatory cooperative yeast partners intermix.
Vertical cross-sections in (A) and (B) were from different growth stages of obligatory cooperative yeast communities starting at total 500 cells/mm2 and 1:1 population ratio. Vertical cross-section …
Figure 3 with 1 supplement
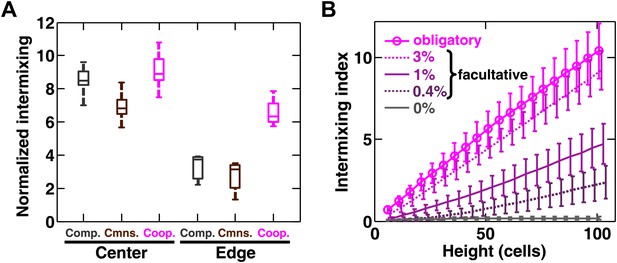
Strongly cooperating populations intermix under a wide range of conditions.
(A) In engineered yeast communities, even though both obligatory cooperative and non-cooperative communities directly above the high-density inoculation spot showed high population intermixing …
-
Figure 3—source data 1
Parameter values used in the fitness model in Figure 3B.
- https://doi.org/10.7554/eLife.00230.020
Figure 3—figure supplement 1
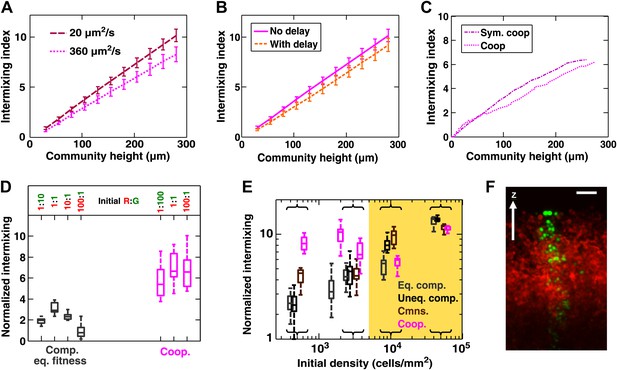
Intermixing is observed in obligatory cooperative communities over a wide range of conditions.
(A) Partner intermixing is insensitive to diffusion constants. In the diffusion model, obligatory cooperative communities with diffusion constants ranging from 20 to 360 µm2/s (corresponding to the …
Figure 4
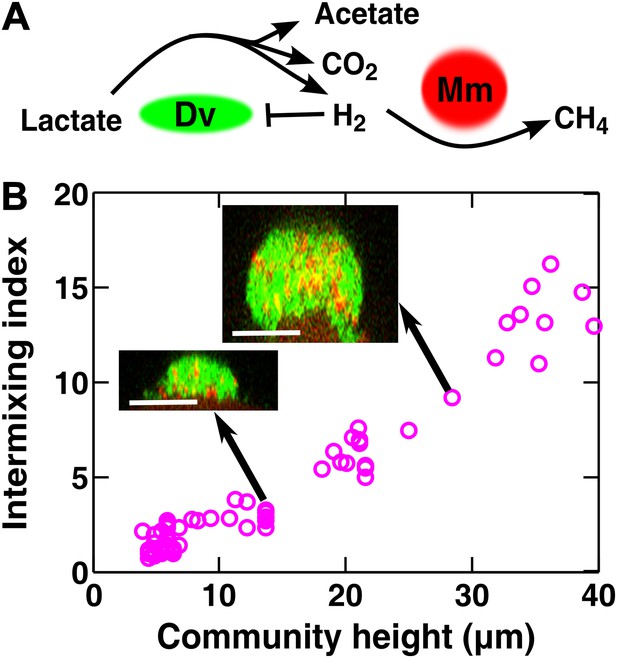
Obligatory cooperation through redox-coupling leads to partner intermixing.
(A) In the absence of sulfate and hydrogen, the bacterium Desulfovibrio vulgaris (Dv) and the archaeon Methanococcus maripaludis (Mm) cooperate through redox coupling. Dv ferments lactate and …
Figure 5 with 1 supplement
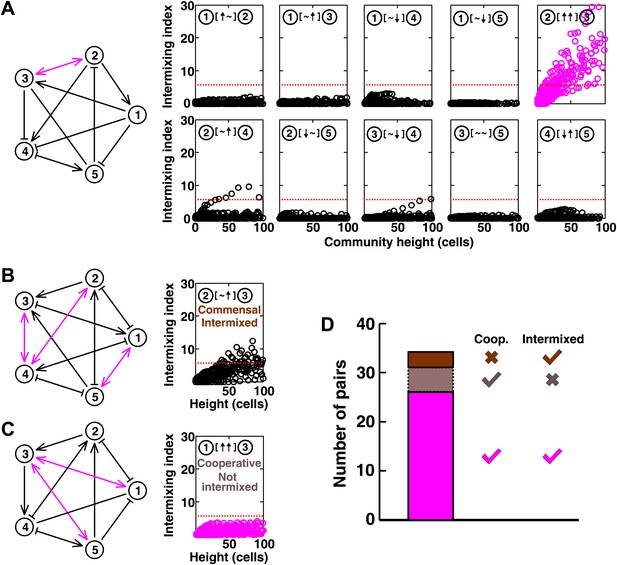
Most of the strongly-cooperative pairs intermixed in simulated five-species communities.
(A-C) Examples of networks in which cooperative pairs intermixed (A), non-cooperative pairs intermixed (B), or cooperative pairs did not intermix (C) are shown. In the schematic network diagrams, …
Figure 5—figure supplement 1
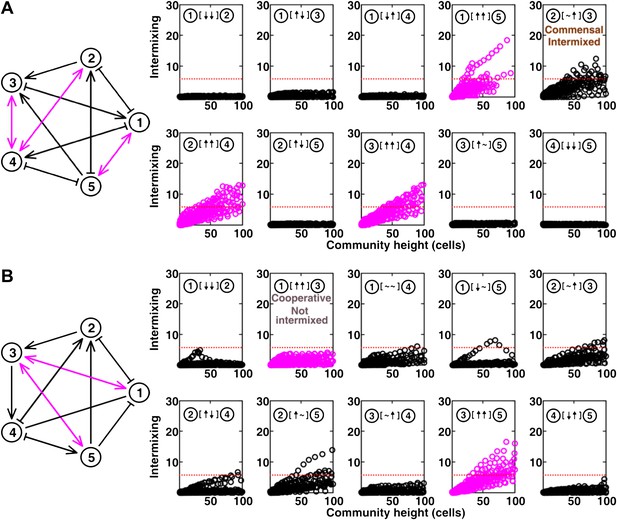
The complete results of Figure 5B and C (panel A and B, respectively).
https://doi.org/10.7554/eLife.00230.024Videos
Video 1
Yeast cells bud to the sides when there is available space and bud upward when sufficiently confined (corresponding to Figure 1—figure supplement 1A). To infer the process of cell rearrangement in …
Video 2
Top views of an equal-fitness competitive community suggest population segregation (corresponding to Figure 2A, left). Competitive communities of strains with equal fitness showed population …
Video 3
In unequal-fitness competition, the fitter population gradually covers the less fit population (corresponding to Figure 2A, right). Here, G is fitter than R. The community started from a uniform …
Video 4
Top views of an obligatory commensal community suggest population layering (corresponding to Figure 2B). For a detailed explanation of the growth kinetics of the community (), please refer to the …
Video 5
Top views of an obligatory cooperative community suggest populations intermixing (corresponding to Figure 2C). For a detailed explanation of the growth kinetics of the community (), please refer …
Tables
Table 1
Summary of steady-state occupancy, conditions to achieve steady-state, and the stability of steady-state for six types of ecological interactions.
| Interaction | Steady-state occupancy | Steady-state condition | Stability |
|---|---|---|---|
| G[∼∼]R | Any | Only when | Unstable |
| G[↑ ↑]R | Globally stable | ||
| G[∼↓]R | Unstable | ||
| G[∼↑]R | Globally stable | ||
| G[↓↓]R | Unstable | ||
| G[↓↑]R | Locally stable (when ; see Figure 1—figure supplement 2) |
Additional files
-
Source code 1
MATLAB code for simulating cooperative communities in the fitness model.
Other ecological interactions can be simulated by changing the values of the interaction parameters r12 and r21.
- https://doi.org/10.7554/eLife.00230.026
-
Source code 2
MATLAB code for simulating cooperative communities in the diffusion model.
In this version, the diffusion constant inside the community is assumed to be similar to the diffusion constant of agarose (Figure 2—figure supplement 2A).
- https://doi.org/10.7554/eLife.00230.027
-
Source code 3
MATLAB code for simulating competitive communities in the diffusion model.
In this version, the diffusion constant inside the community is assumed to be smaller than the diffusion constant of agarose (Figure 2—figure supplement 2B).
- https://doi.org/10.7554/eLife.00230.028
-
Source code 4
MATLAB function for in-plane rearrangement of cells in both the fitness and the diffusion models.
- https://doi.org/10.7554/eLife.00230.029
