Cellular resolution models for even skipped regulation in the entire Drosophila embryo
- European Molecular Biology Laboratory, European Bioinformatics Institute, Wellcome Trust Genome Campus, United Kingdom
- Okinawa Institute of Science and Technology Graduate University, Japan
- Microsoft Research Cambridge, United Kingdom
- University of Cambridge, United Kingdom
- Harvard Medical School, United States
- University College London, United Kingdom
- London Research Institute, Cancer Research UK, United Kingdom
Figures
Figure 1 with 1 supplement
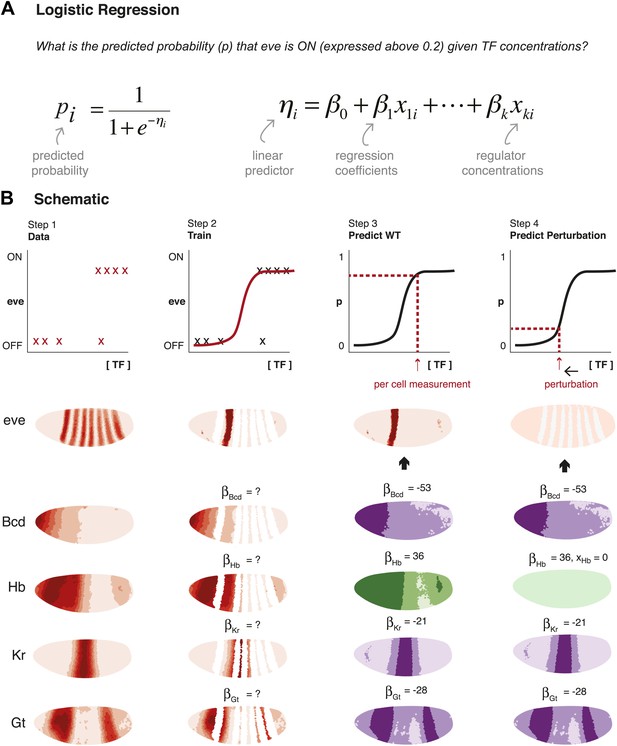
Schematic representation of method used to model eve expression.
(A) Logistic regression is used to calculate the probability pi that eve is ON in a given nucleus i, given TF concentrations. A logistic model linearly combines the values of independent variables (in this case, the concentrations, xki, of regulators 1 to k) to produce a prediction; the predictor, ηi, is then transformed by the logistic function to give the probability, pi, of eve being ON. The weight parameters βk are optimized to provide the best fit with the training data: positive weights indicate activators and negative weights indicate repressors. (B) Schematic representation of the data preparation, model training and prediction steps using eve stripe 2 as an example. The plots represent how logistic regression operates; the lateral perspectives of the embryo show the Virtual Embryo and processed expression data for eve and four regulators (Bcd, Hb, Kr, and Gt). In Step 1, eve’s expression is discretized whereas TF concentrations are retained as continuous values. Each nucleus corresponds to a data point. In Step 2, the logistic model is trained to classify whether eve is ON or OFF using all nuclei in stripe 2, and all OFF nuclei in the embryo. In Step 3, the trained model is used to predict eve expression in every nucleus of the entire embryo using the concentrations of the relevant regulators within them (shown in green for activators, and purple for repressors). In Step 4, the effects of perturbations are predicted by adjusting the concentration of the regulator under consideration (in this case, Hb), but without changing any model parameters.
Figure 1—figure supplement 1
Expression of eve across the anteroposterior axis.
Each strip shows the expression of eve in a narrow lateral band (10 μm either side of the lateral midline) along the anteroposterior (A-P) axis for each time point (1–6) in the Virtual Embryo. The interval between the time points is approximately 10 min. The horizontal line is the threshold of 0.2 used in training the models. The rug plot indicates which nuclei are considered within the stripes according to this threshold.
Figure 2 with 4 supplements
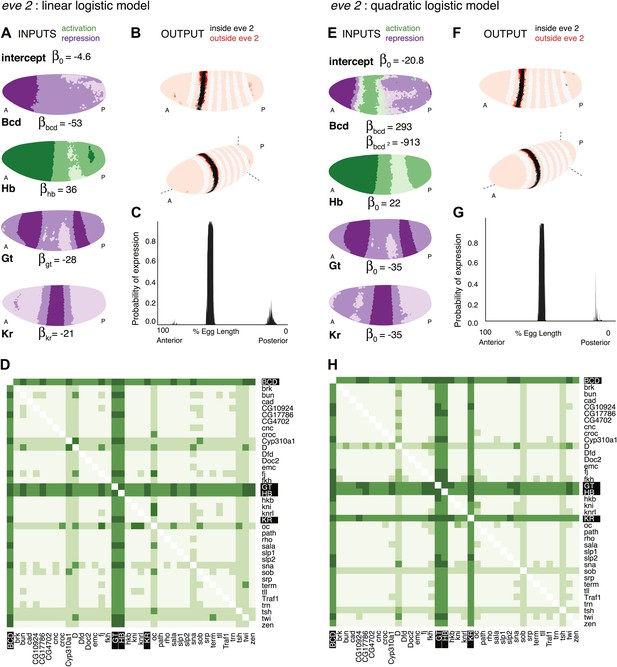
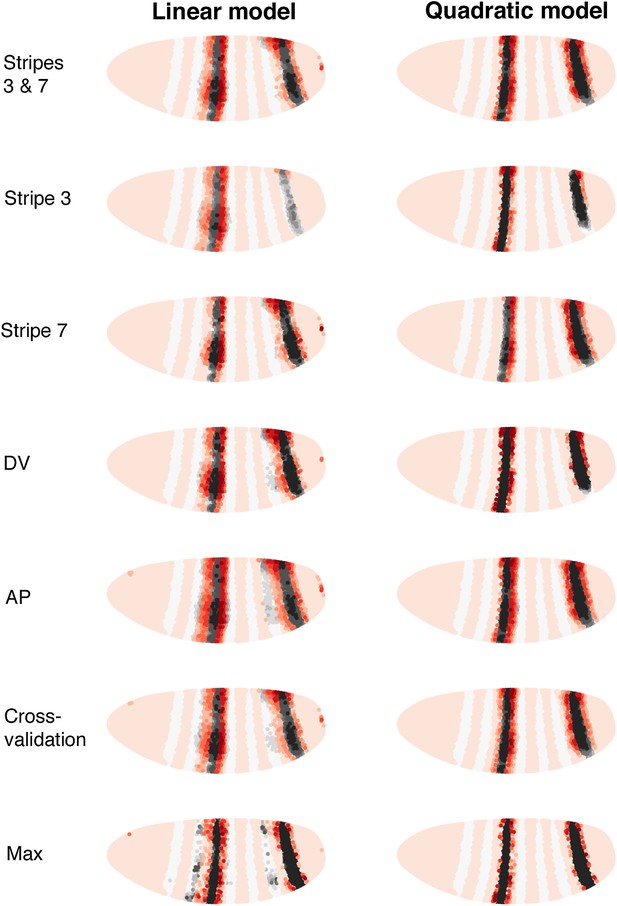
Logistic models accurately predict eve 2 expression.
(A) Lateral perspectives of the Drosophila embryo depicting the contribution of four regulators (Bcd, Hb, Gt, and Kr) to the model output. Embryos are drawn with the anterior (A) to the left and posterior (P) to the right, along with regulator names and corresponding coefficients in the model. Each nucleus is shaded to indicate the level of contribution by regulators, with darker colors signifying stronger effects (in this case, due to higher regulator concentrations): green represents a positive, activating effect and purple a negative, repressive one. Inputs are continuous, but drawn using a discrete color scale for simplicity. (B) Lateral and 3D perspectives of the embryo show the model prediction of eve stripe 2 expression. Each nucleus is colored from light to dark for low to high probability of eve being ON: within stripes the color scale is from white to black and outside the stripes it is on a red scale, with peach for values below 0.15. (C) A ribbon plot showing the probability of eve expression (y-axis) for nuclei within 10 μm of the lateral midline along the anteroposterior axis (x-axis). The plot demonstrates that the stripe borders are sharply defined. It also allows easy comparisons with other models that are generally performed in one dimension. (D) For regulator discovery, for every possible pair of regulators, we determined the best-scoring model of four regulators containing the pair. The 38 regulators in the dataset are shown on the x- and y-axes of the heat map, and the highest scores for every pair are depicted in the intersecting cell on a color scale from light (minimum score in the heat map) to dark (highest score in the heat map). Regulators making consistently informative contributions to models can be identified by the dark bands running across the heat map. Using linear logistic models, Gt, Hb and Bcd can be clearly seen to be informative regulators (highlighted in black). (E–G) Prediction made using a quadratic logistic model, in which Bcd is assigned a concentration-dependent dual regulatory activity: it is an activator (green) at low concentrations in the region of stripe 2, and a repressor (purple) at higher concentrations everywhere else. The model outputs a better prediction for stripe 2 expression as shown in Table 1. Most importantly, it reconciles Bcd’s apparently paradoxical behavior compared with the literature (Small et al., 1992; Andrioli et al., 2002). (H) Regulator discovery using quadratic models identifies Gt, Hb, Bcd, and Kr as informative regulators (highlighted in black).
Figure 2—figure supplement 1
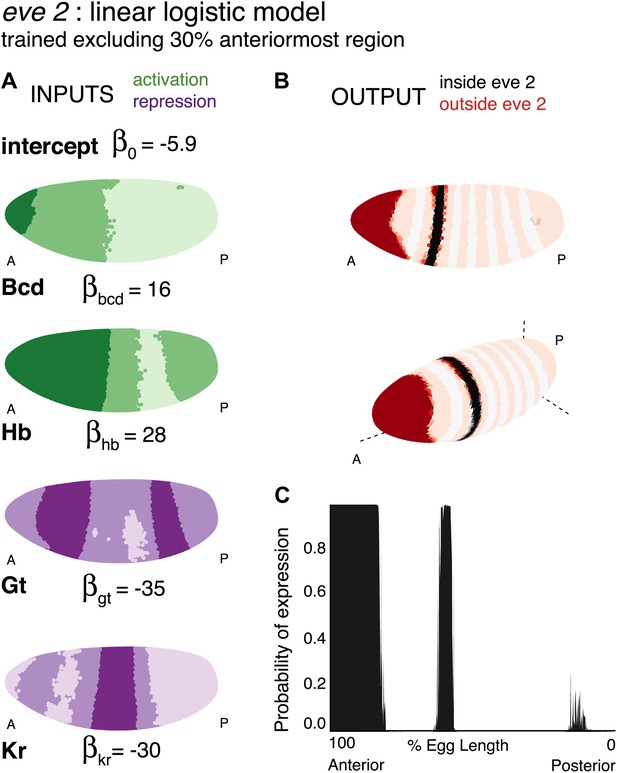
Training the linear model without the anteriormost region gives Bcd an activating role.
Regulator inputs and model output are shown as in Figure 2. (B) and (C) The stripe is still sharply defined when the anteriormost region is excluded. (A) Bcd is activating in stripe 2, but more strongly in the anterior.
Figure 2—figure supplement 2
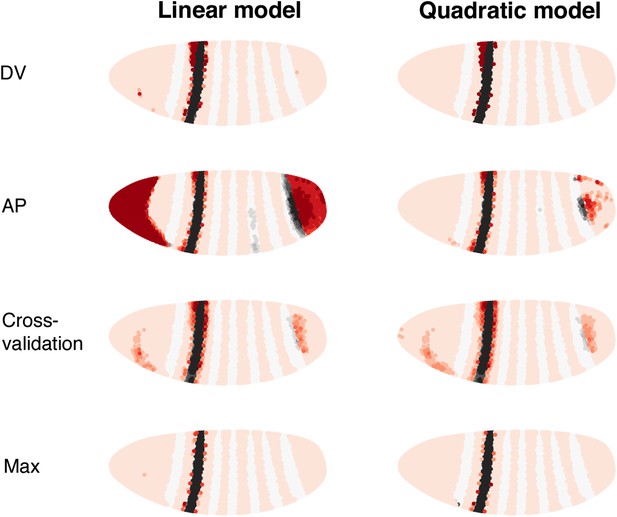
Consistency of the eve 2 linear and quadratic models (DV, AP and cross-validation).
The linear and quadratic models are trained as in the main text, but with the dataset initially restricted. DV is restricted to 20 μm on either side of the lateral mid-line. AP includes only the stripe and its immediately neighboring nuclei. Cross-validation is the average of 100 predictions each trained on a random subset of 50 nuclei (out of 2936). (Max) makes use of all 38 candidate regulators, but with the same training data as the models described in the main text.
Figure 2—figure supplement 3
The linear logistic regression model is not unreasonably flexible: a given set of regulators cannot fit any stripe well.
A logistic model for Hb, Bcd, Kr, and Gt is fit using training data that is selected as described in the main text for each stripe (1–7, right axis). The predictions (left axis) for each nucleus are plotted along the whole anteroposterior axis, but for clarity, only the predictions for the nuclei within 10 μm either side of the lateral midline are shown.
Figure 2—figure supplement 4
The quadratic logistic regression model is not unreasonably flexible: a given set of regulators cannot fit any stripe well.
A logistic model for Hb, Bcd, Kr and Gt, including a quadratic term for Bcd, is fit using training data that is selected as described in the main text for each stripe (1–7, right axis). The predictions (left axis) for each nucleus are plotted along the whole anteroposterior axis, but for clarity, only the predictions for the nucleus within 10 μm either side of the lateral midline are shown.
Figure 3
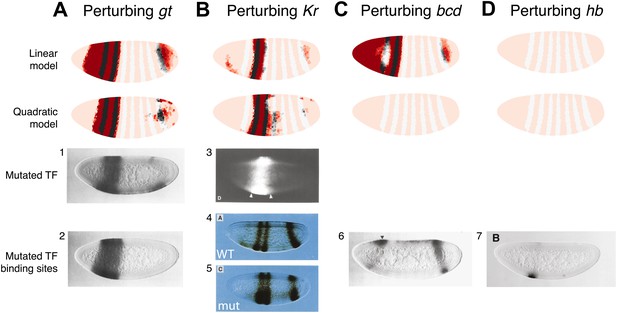
The quadratic model accurately predicts eve 2 expression under perturbation of input TFs.
The effects of regulatory perturbations on stripe 2 expression are predicted by altering regulator concentrations but keeping all the model coefficients unchanged; for TF deletion or binding site mutants, this involves setting the relevant regulator’s concentrations to 0. Predictions are made for perturbations using the linear and quadratic models. Comparisons to experiments provide robust, independent validations of model predictions. Loss of (A) gt or (B) Kr causes eve expression to extend towards the anterior and posterior of the embryo respectively, in excellent agreement with experimental evidence. (C) For the bcd mutant, the linear model predicts expression at the anterior of the embryo, something that is not observed in experiments. In contrast, the quadratic model does not suffer from this. (D) Perturbing hb leads to complete loss of eve stripe 2 for both models. The better agreement between predictions and experimental evidence suggests that the quadratic is a more plausible model of eve 2 regulation.
In situ images in panels 1, 2, and 6 are reproduced from Figure 4B–C and 6C, Small et al. (1992), The EMBO Journal; Nature Publishing Group has granted permission to reproduce these images under the terms of the Creative Commons Attribution 3.0 Unported License (CC BY 3.0).
© 1991, Cold Spring Harbor Laboratory Press, All Rights Reserved. The in situ image in panel 3 is reprinted with permission from Figure 2D, Small et al. (1991), Genes & Development.
© 1991, American Association for the Advancement of Science, All Rights Reserved. In situ images in panels 4 and 5 are reprinted with permission from Figure 3A and 3C, Stanojevic et al. (1991), Science.
© 1996, The Company of Biologists, All Rights Reserved. The in situ image in panel 7 is reproduced with permission from Figure 6B, Arnosti et al. (1996), Development.
Figure 4 with 7 supplements
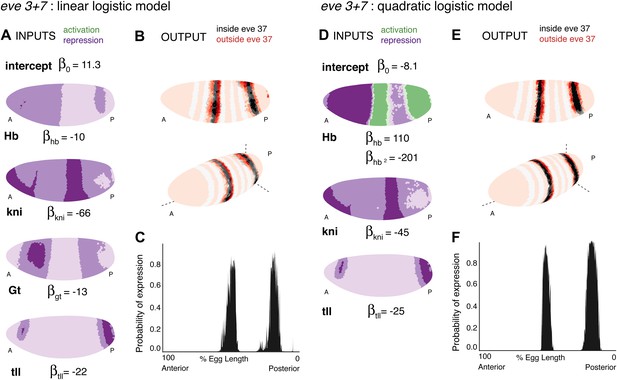
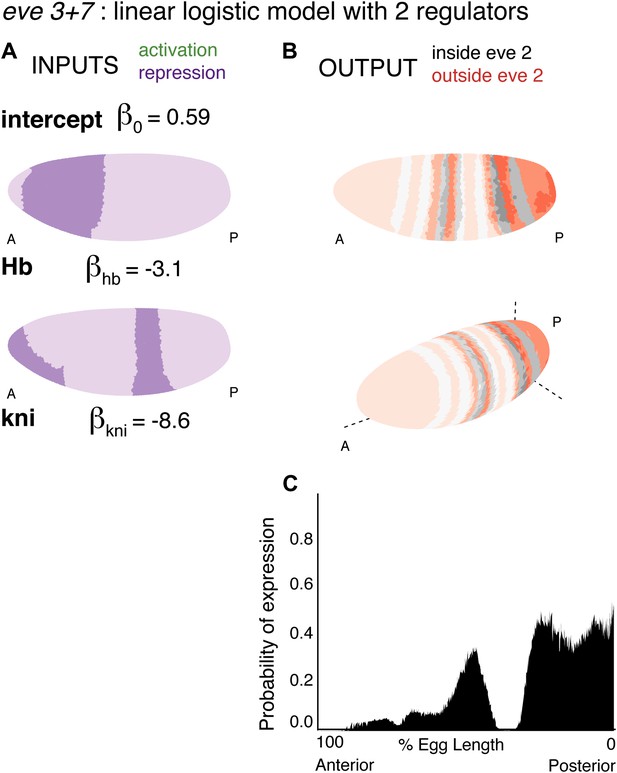
Linear and quadratic logistic models accurately predict eve 3+7 expression.
Regulator inputs and model output are shown as in Figure 2. (A–C) The linear model including Hb, kni, tll, and Gt; (D–F) the quadratic model comprises Hb, kni, and tll, with a quadratic term for Hb as a concentration-dependent dual regulator. Both models clearly define the two stripes, though the midline ribbon plots show that the quadratic model defines the sharpest borders. The initial predictions therefore suggest that the quadratic model provides the best output.
Figure 4—figure supplement 1
Hb and kni are not sufficient for a good model fit.
Regulator inputs and model output are shown as in Figure 2. (A–C) The linear logistic model with only Hb and kni does not repress expression to the posterior of stripe 7.
Figure 4—figure supplement 2
A linear logistic model with Hb, kni and tll does not have sharp stripe borders.
Regulator inputs and model output are shown as in Figure 2. (A–C) The linear logistic model with Hb, kni and tll does not produce as sharp borders as the models in Figure 4.
Figure 4—figure supplement 3
Consistency of the eve 3+7 linear and quadratic models.
(Stripe 3, Stripe 7, DV, AP and Cross-validation) The linear and quadratic models are trained as in the main text, but with the dataset initially restricted. Stripe 3 is trained using stripe 3 and the nuclei that are outside of the stripes (OFF). Stripe 7 is trained using stripe 7 and the nuclei that are outside of the stripes (OFF). DV is restricted to 20 μm on either side of the lateral mid-line. AP includes only the stripes and their immediately neighboring nuclei. Cross-validation is the average of 100 predictions each trained on a random subset of 50 nuclei (out of 3481). (Max) makes use of all 38 candidate regulators, but with the same training data as the models described in the main text.
Figure 4—figure supplement 4
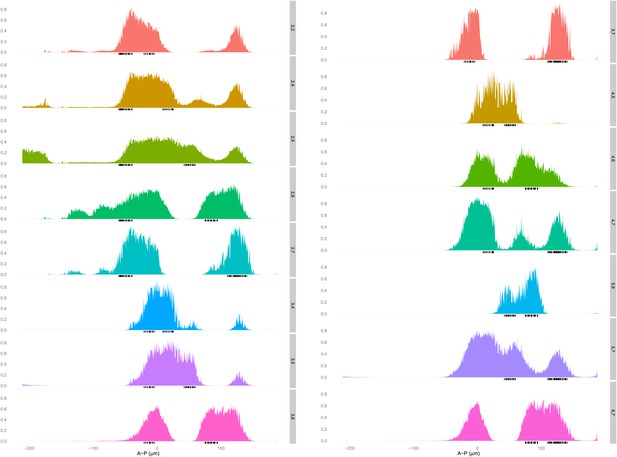
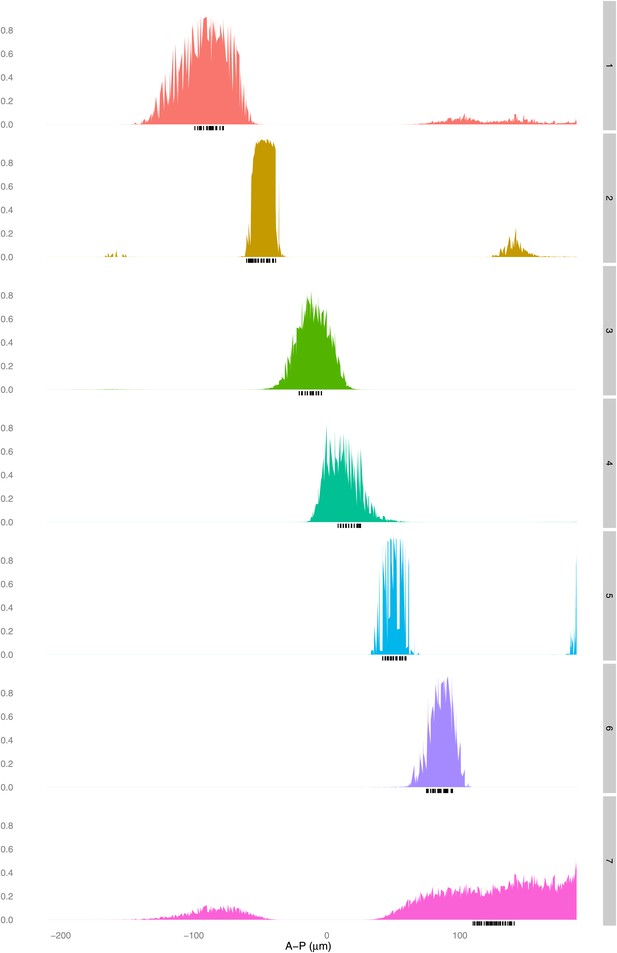
The linear logistic regression model is not unreasonably flexible: a given set of regulators cannot fit any pair of stripes well.
A logistic model for Hb, kni, tll, and Gt is fit using training data that is selected as described in the main text for each pair of stripes excluding stripe 1 (right axis). The predictions (left axis) for each nucleus are plotted along the whole anteroposterior axis, but for clarity, only the predictions for the nuclei within 10 μm either side of the lateral midline are shown.
Figure 4—figure supplement 5
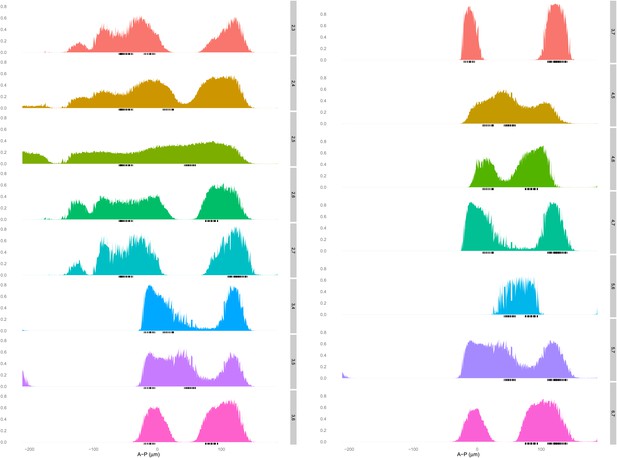
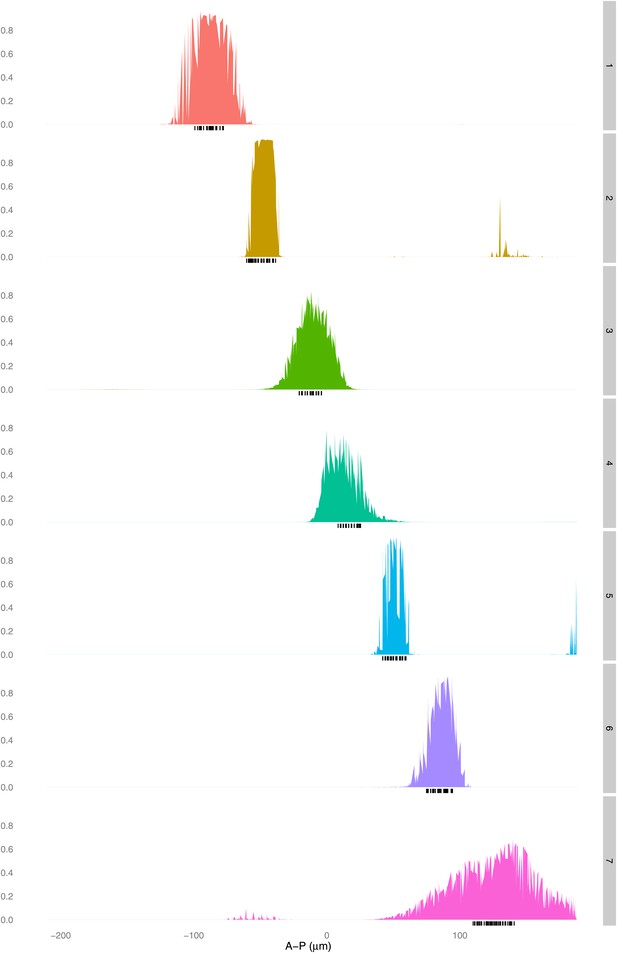
The quadratic logistic regression model is not unreasonably flexible: a given set of regulators cannot fit any pair of stripes well.
A logistic model for Hb, kni, and tll, including a quadratic term for Hb, is fit using training data that is selected as described in the main text for each pair of stripes excluding stripe 1 (right axis). The predictions (left axis) for each nucleus are plotted along the whole anteroposterior axis, but for clarity, only the predictions for the nuclei within 10 μm either side of the lateral midline are shown.
Figure 4—figure supplement 6
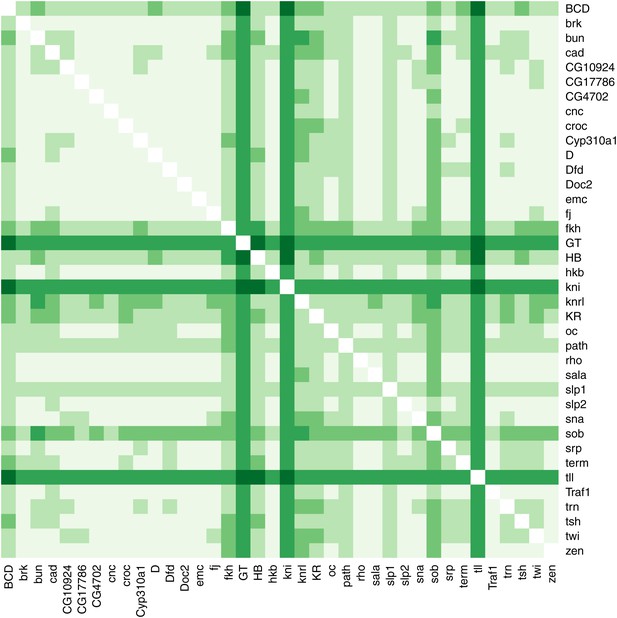
Regulatory discovery for a linear logistic model of eve 3+7.
Regulatory discovery is as shown in Figure 2D. For every possible pair of regulators, we determined the best-scoring model of four regulators containing the pair. The 38 regulators in the dataset are shown on the x- and y-axes of the heat map, and the highest scores for every pair are depicted in the intersecting cell on a color scale from light (minimum score in the heat map) to dark (highest score in the heat map). Regulators making consistently informative contributions to models can be identified by the dark bands running across the heat map. Here, Gt, kni, and tll can be seen to be informative regulators.
Figure 4—figure supplement 7
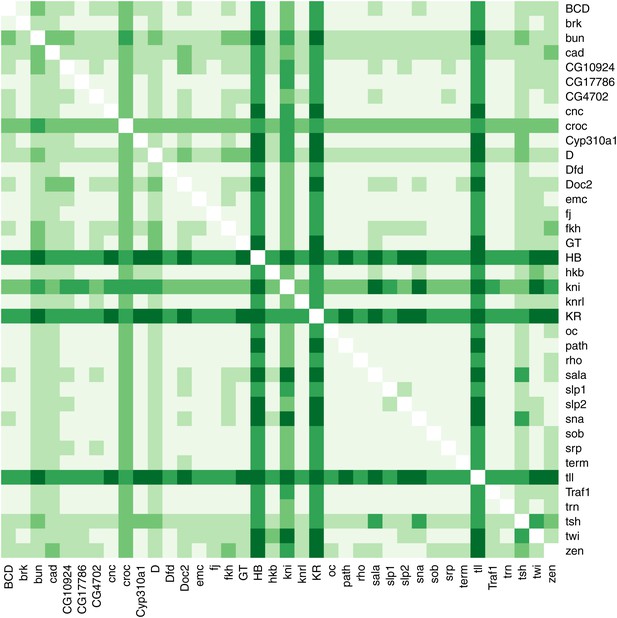
Regulatory discovery for a quadratic logistic model of eve 3+7.
Regulatory discovery is as shown in Figure 2H. For every possible pair of regulators, we determined the best-scoring model of four regulators containing the pair. The 38 regulators in the dataset are shown on the x- and y-axes of the heat map, and the highest scores for every pair are depicted in the intersecting cell on a color scale from light (minimum score in the heat map) to dark (highest score in the heat map). Regulators making consistently informative contributions to models can be identified by the dark bands running across the heat map. Here, Hb, kni, Kr, and tll can be seen to be informative regulators.
Figure 5 with 3 supplements
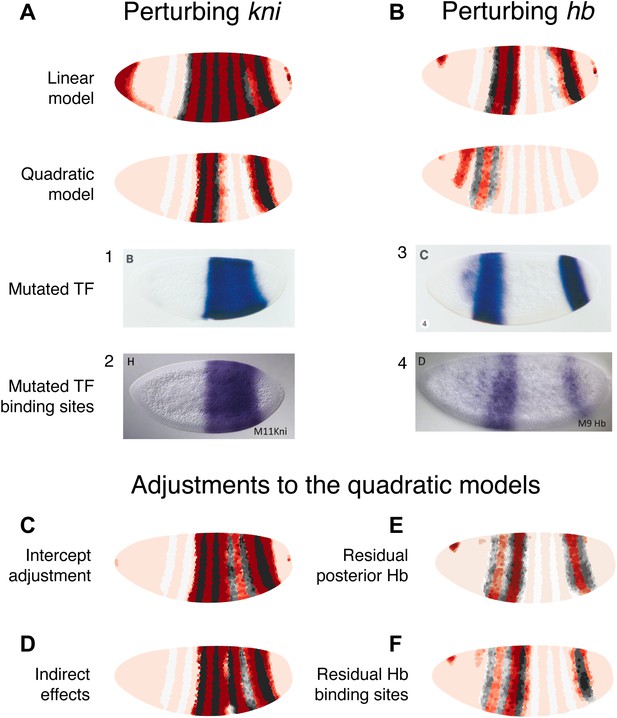
Linear and quadratic logistic models accurately predict eve 3+7 expression under perturbation of Kni and Hb.
The effects of regulatory perturbations on eve 3+7 expression are predicted as described in the main text. (A) Perturbation of kni and its binding sites cause full reporter expression between the stripes. The linear model predicts this observed extension, but the quadratic does not. (B) Perturbation of hb causes stripe 3 to expand and move anteriorly, and stripe 7 to expand slightly. Binding site mutations show similar effects, though perhaps without the anterior shift of stripe 3. The linear model provides good prediction of both stripes. The quadratic produces a good stripe 3 prediction, including its anterior shift, but fails to predict any expression in stripe 7. (C–F) Given the initial preference for the quadratic, we considered minor and biological plausible assumptions that allow the model to make accurate predictions. For the kni mutants, these are (C) the minor adjustment of the intercept and (D) inclusion of indirect effects of kni on hb by increasing Hb by 50% of wild-type kni. For the hb mutants, these are (E) the inclusion of residual maternal Hb in the posterior and (F) simulating the effects of residual Hb binding sites.
In situ images in panels 1 and 3 are reprinted with permission from Figure 4B–C, Small et al. (1996), Developmental Biology (© copyright Elsevier, 1996, All Rights Reserved). In situ images in panels 2 and 4 are reproduced with permission from Figures 4H and 6D, Struffi et al. (2011), Development (© copyright The Company of Biologists, 2011, All Rights Reserved).
Figure 5—figure supplement 1
Indirect effects and the quadratic model can explain the expansion and retreat of expression observed in the eve 3+7 reporter in a kni mutant.
Since Kni represses Hb, the loss of kni may lead to an increase of Hb towards steady state. To approximate this, Hb was added in increasing proportion, from 20% to 150%, of wild-type kni expression. The resulting eve 3+7 quadratic prediction is shown in a kni mutant.
Figure 5—figure supplement 2
An adjustment to the intercept in the quadratic logistic model for eve 3+7 results in a slight expansion of expression between the stripes.
This prediction shows the effect of increasing the intercept by 4.5. This change in the intercept corresponds to potential differences in expression between the endogenous gene and the transgenic reporter.
Figure 5—figure supplement 3
Hb binding site mutants may dampen or remove Hb repression at higher concentrations.
Dampening the effect of Hb at higher concentrations, for example by as shown in the center plot, changes the regulatory impact of Hb in the embryo (left and right plots). The left plot shows Hb activating at low concentrations and repressing at high concentrations; the right plot shows an attenuation of this effect leading instead to a weakening in activation. The corresponding predictions are shown below.
Figure 6
Models predict eve 2 and 3+7 expression at earlier time points.
Model predictions for earlier time points in the Virtual Embryo are shown for the (A) eve 2 and (B) eve 3+7 linear and quadratic models. The time points are labeled from the start of the dataset; the third time point is the one used throughout the main text. For eve 2, the linear and quadratic models show a wider stripe at the second time point and a well-defined stripe at time point 3. This matches the in situ images below from Andrioli et al. (2002) which show a transgenic reporter at early and mid cycle. The predictions for eve 3+7 are consistent in terms of the positions of the stripes, with stripe 3 appearing earlier than stripe 7. At the earlier time points the difference in sharpness of the stripe borders between the quadratic and linear model is more pronounced suggesting that the interpretation of positional information by the quadratic model is more stable and precise.
The in situ image for eve 3+7 is reprinted with permission from Figure 2C, Small et al. (1996), Developmental Biology (© copyright Elsevier, 1996, All Rights Reserved). In situ images for eve 2 are reproduced with permission from Figure 4A,B, Andrioli et al. (2006), Development (© copyright The Company of Biologists, 2006, All Rights Reserved).
Figure 7 with 1 supplement
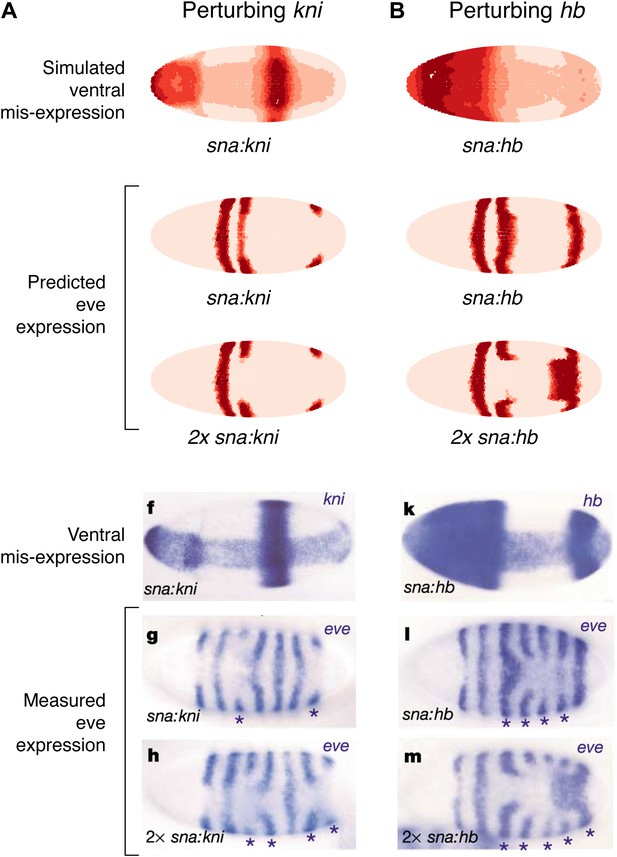
Quadratic models accurately predict fine-scale features of expression patterns due to input misexpression.
The study by Clyde et al. (2003) misexpressed hb and kni along the ventral surface of the embryo using transgenes driven by a snail promoter and recorded the effects of one or two copies of these transgenes on eve expression. We replicated these experiments using quadratic models for eve 2 and eve 3+7 (trained on stripe 3), by adding Hb and kni in proportion to the distribution of snail in the Virtual Embryo dataset. As described in the main text, we also added an indirect effect from Hb activating Kr. (A) With kni misexpression, the model accurately predicts the thinning (x1 transgene), then cutting of stripe 3 (x2). (B) With Hb misexpression, the model successfully predicts the bulging, then cutting and bending of stripe 3 (x2), and the bulging of stripe 7 (x2). Stripe 2 remains unaffected in both perturbations, in agreement with the experimental results. The accuracy of the predictions indicates that the quadratic model for eve 3+7 can explain the experimental results very well. In contrast the linear models are unable to predict these results.
In situ images are reproduced from Figures 1F–H and 1K–M, Clyde et al. (2003), published in Nature; Nature Publishing Group has granted permission to reproduce these images under the terms of the Creative Commons Attribution 3.0 Unported License (CC BY 3.0).
Figure 7—figure supplement 1
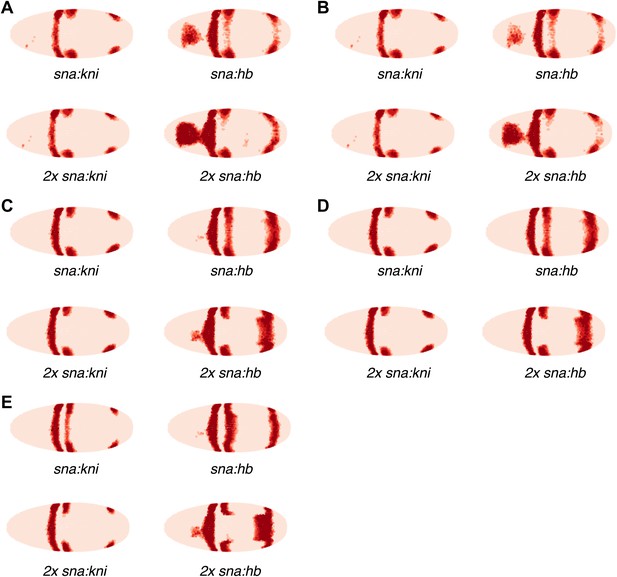
Supplementary misexpression predictions of the eve 2 and eve 3+7 linear (A,B) and quadratic (C–E) models.
(A, C and E) have no indirect effects, whereas (B and D) include a hypothetical indirect effect mediated by Hb activating Kr. This is modeled by adding Kr in proportion (50%) to the increase of Hb. The eve 3+7 model in (A–D) was trained on stripes 3 and 7, whereas in (E) it was trained on stripe 3 only. The predictions are shown for one (x1) and two (x2) copies of the hb and kni transgenes as described in the main text.
Tables
Table 1
Measurements quantifying the accuracy of eve 2 predictions
| Model | In the stripe (%) | Immediate neighbors (%) | 2nd degree neighbors (%) |
|---|---|---|---|
| eve 2 linear logistic | 86 | 23 | 2 |
| eve 2 quadratic logistic | 93 | 21 | 2 |
-
The table shows the percentage of nuclei with predicted eve expression (p>0.5). This is a stringent measure of the accuracy of classification, and is particularly useful for assessing the accuracy of the stripe borders. Nuclei with eve expression>0.2 are defined as those ‘in the stripe’; neighboring nuclei are outside this thresholded region, either immediately adjacent to it, or two nuclei away. A perfect prediction should identify all stripe 2 nuclei as having a high probability of ON with the probability of being ON dropping off rapidly further from the stripe. Though both linear and quadratic models output excellent predictions, the latter provides a slightly more accurate fit to the data.
Table 2
Measurements quantifying the accuracy of eve 3+7 predictions
| Model | In the stripe (%) | Immediate neighbors (%) | 2nd degree neighbors (%) |
|---|---|---|---|
| eve 3+7 linear logistic | |||
| kni and Hb | 0 | 0 | 0 |
| kni, Hb, and tll | 56 | 39 | 27 |
| kni, Hb, tll, and gt | 76 | 37 | 17 |
| eve 3+7 quadratic logistic | 86 | 39 | 9 |
-
The table shows similar measures of accuracy for stripes 3 and 7 as in Table 1. It is clear that the quadratic model and the 4-regulator linear model provide the best predictions, with the most sharply defined borders.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Cellular resolution models for even skipped regulation in the entire Drosophila embryo
eLife 2:e00522.
https://doi.org/10.7554/eLife.00522
