Buffered Qualitative Stability explains the robustness and evolvability of transcriptional networks
- University of Dundee, United Kingdom
Figures
Figure 1
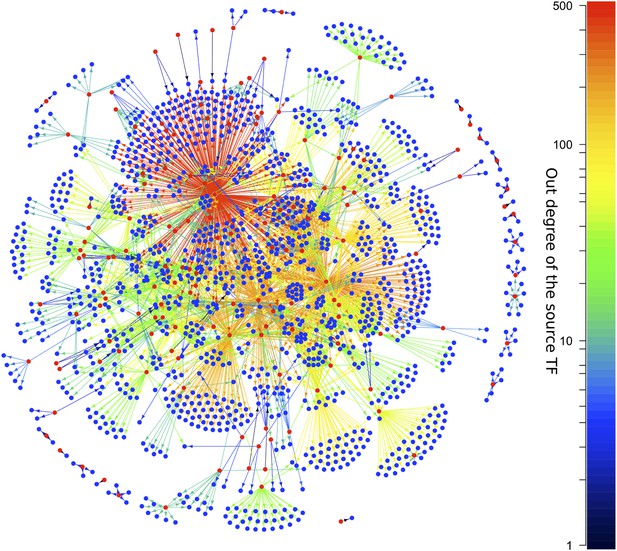
The E. coli GRN.
The E. coli GRN derived from Salgado et al. (2012) using two evidence codes. Genes that are reported to regulate transcriptionally at least one other gene, that is transcription factors (TFs), are represented as red circles; the other genes are represented by blue circles. Arrows indicate a transcriptional interaction from the TF to the target gene. The arrows are colour-coded according to the number of genes regulated by the source TF. Note the logarithmic scale in the colour coding.
Figure 2 with 4 supplements
Feedback loops in real and simulated GRNs.
Number of feedback loops is provided on a logarithmic scale for E. coli (A), S. cerevisiae (B), and the human GM12878 cell line (C) and in each case is compared with a randomly simulated network containing the same number of genes, TFs, and connections. For the random networks, each graph reports the mean and standard deviation. (D) Schematic illustrations of feedback loops of length 2–6 are plotted in black.
Figure 2—figure supplement 1
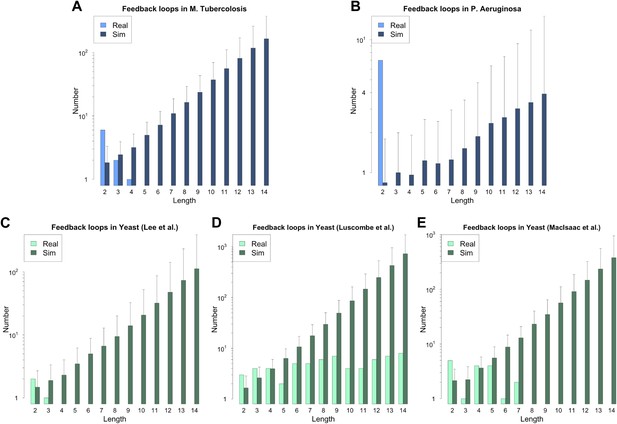
Feedback loops in M. tuberculosis, P. aeruginosa and other yeast datasets.
Number of feedback loops is provided on a logarithmic scale for M. tuberculosis (A), P. aeruginosa (B), the yeast dataset derived from Lee et al. (C), the yeast dataset derived from Luscombe et al. (D), and the yeast dataset derived from MacIsaac et al. (E). In each case the real dataset is compared with a randomly simulated network containing the same number of genes, TFs and connections. For the random networks, each graph reports the mean and standard deviation. Note that Luscombe et al. (2004) was mainly concerned with the dynamics of yeast GRN and built the full GRN in such a way to better stress differences under different growth conditions. The dataset was constructed by adding to the network derived by Lee et al. (2002) new interactions derived under different experimental conditions, and the absence of a measure of confidence for the interactions makes it difficult to assess the strength of the experimental support for the interactions that form the feedback loops. The above considerations suggest that a moderate rate of false positives may be present in the dataset. The sensitivity of loop count to noise in the data therefore suggests that loop counting may not provide a good indication of the role of BQS by itself in this case. Moreover, MacIsaac et al. (2006) takes a computational approach to the construction of the GRN of S. cerevisiae using the experimental data provided by Harbison et al. (2004) as a starting point. Therefore, noisy data should be expected and caution should be used in interpreting the data. The network used was the most statistically restrictive. Although a limited number of long feedback loops is present in the dataset (E), comparison with random data indicates that this number is much smaller than expected by chance, still suggesting a selective pressure against instability. Note how the number of long feedback loops is extremely limited for the dataset derived from direct biological experimentation (A–C).
Figure 2—figure supplement 2
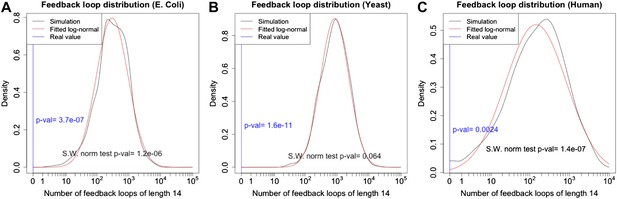
p-Value estimation for the number of long feedback loops.
The theoretical probability density function of the number of feedback loops of a given length is not well characterized. However, calling nloops the number of feedback loops of a given length in a single simulation, the transformation appears to produce normally distributed data in all the datasets analysed. The normality of the distribution was supported by the Shapiro–Wilk normality test. Using this transformation it is possible to estimate the probability of having no feedback loops of length 14 in a random graph. (A–C). The data for E. coli, yeast and human (black line) support quite well the fitted log-normal distribution (red line), as expected from the very low p-value of the Shapiro–Wilk normality test. Analysing the number of loops of a specific length was preferred to performing an analysis combining the information on the number of loops of different length. This choice was made due to the non-independence of the number of loops of different length.
Figure 2—figure supplement 3
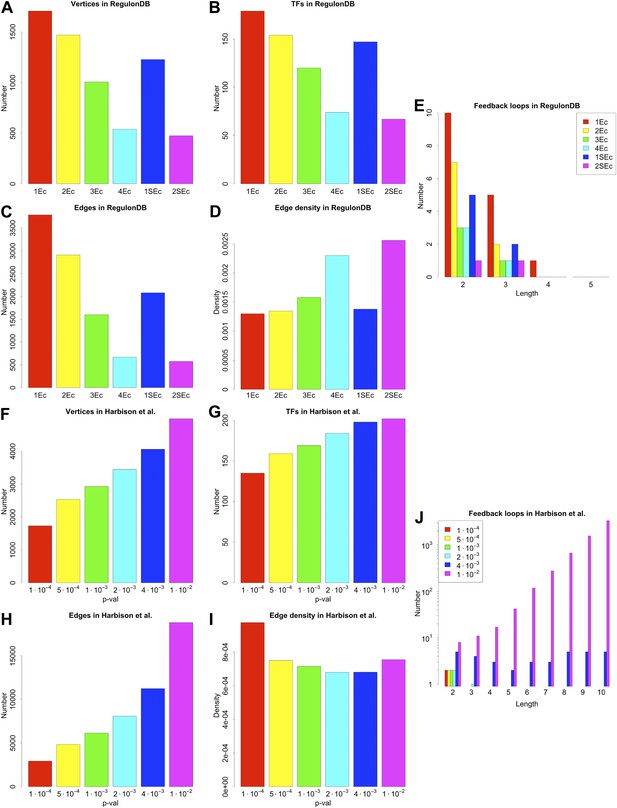
General properties and number of feedback loops in the RegulonDB (E. coli) and Harbison et al. (yeast) datasets under different statistical conditions.
RegulonDB reports, for each interaction, a list of evidence codes indicating which experimental techniques reported a particular interaction. Some of these codes (called `strong’) are associated with particularly reliable biological techniques (Salgado et al., 2012). The information provided by RegulonDB can be used in different ways to assess the statistical validity of our analysis. A first approach is to use the number of evidence codes as an indicator of the confidence level of an interaction: the larger the number of evidence codes, the greater the confidence. A second approach is to restrict the network only to those interactions supported by strong evidence codes. We decided to study the effect of varying the number of general or strong evidence codes on the results discussed. ‘kEc’ indicates the network constructed using only those interactions supported by at least k evidence codes, while ‘kSEc’ indicates the network constructed using only those interactions supported by at least k strong evidence codes. The number of genes (A), TFs (B), and interactions of the networks (C) vary with the number of evidence codes. However, the edge density (D) is rather stable, suggesting that the global properties of the GRN are mostly preserved in the different types of network. The number of feedback loops is very limited regardless of the number of evidence codes used (E). 2Ec and 2SEc have similar edge density (D) and number of illegal feedback loops (E), thus suggesting that taking two evidence codes gives a network similar to the one obtained by considering only strong biological evidence. In the yeast dataset derived by Harbison et al. (2004) each interaction is associated with a p-value that measures the probability that such an interaction has been detected due to experimental error. Selecting a large threshold p-value increases the probability of false positives, but decreases the probability of false negatives. Lee et al. (2002) reported that a threshold p-value of 10–3 provides a good trade-off for this kind of data. However, a reliable theory would be expected to display a limited sensitivity to a small variation of the threshold. The number of genes (F), TFs (G), and interactions of the network (H) change with different thresholds. Nevertheless, the edge density is quite stable (I). As with the RegulonDB data (A–D), these results suggest that the main characteristics of the network are mostly preserved under different statistical constrains. The number of feedback loops remains low for reasonable variations around the selected threshold (J), and the increase in number is compatible with the expected increase in the rate of false positives. Interestingly, looking at feedback loop number, a ‘phase transition’ becomes apparent for large thresholds. This behaviour suggests the use of great care when performing this type of analysis on very noisy data.
Figure 2—figure supplement 4
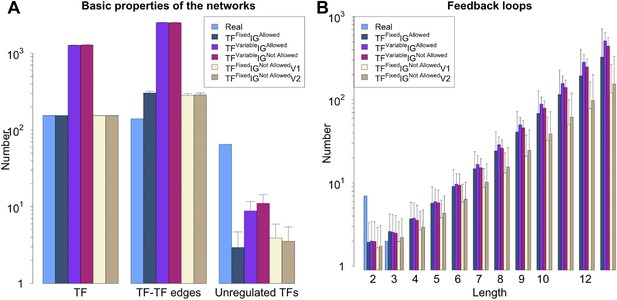
General properties and number of feedback loops under different random model for RegulonDB (E. coli).
The different constraints (and algorithms) disused in ‘Materials and methods’ result in different networks properties. (A) Number of TFs, number of regulatory connections among TFs and number of unregulated TFs. (B) Despite the different properties (A), all the random models considered display a number of feedback loops strikingly different from the real data.
Figure 3 with 5 supplements
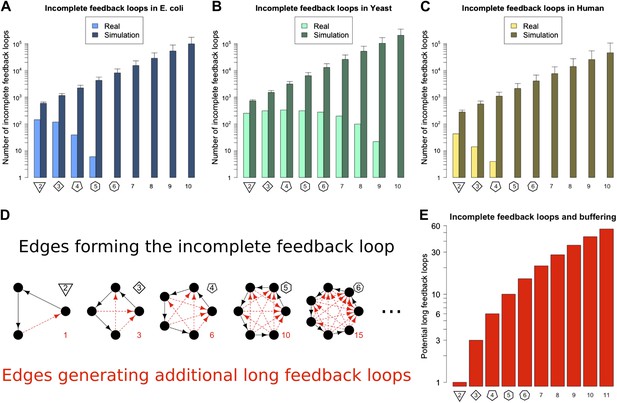
Incomplete feedback loops in real and simulated GRNs.
Number of incomplete feedback loops is provided on a logarithmic scale for E. coli (A), S. cerevisiae (B), and the human GM12878 cell line (C) and in each case is compared with a randomly simulated network containing the same number of genes, TFs, and connections. For the random networks, each graph reports the mean and standard deviation. (D) Schematic illustrations of incomplete feedback loops of length 2–6 are plotted in black, with the edge whose additions would result in additional long feedback loops plotted in red. (E) The number of long loops (>2 nodes) that can be created by the addition of a single new connection to incomplete loops of the specified length (numerical values also given in red text in panel D).
Figure 3—figure supplement 1
Incomplete feedback loops in P. aeruginosa, M. tuberculosis and other yeast datasets.
Number of incomplete feedback loops is provided on a logarithmic scale for M. tuberculosis (A), P. aeruginosa (B), the yeast dataset derived from Lee et al. (C), the yeast dataset derived from Luscombe et al. (D), and the yeast dataset derived from MacIsaac et al. (E). In each case the real dataset is compared with a randomly simulated network containing the same number of nodes and connections. For the random networks, each graph reports the mean and standard deviation. Note how the number of incomplete feedback loops decreases rapidly for the more validated datasets (A–C).
Figure 3—figure supplement 2
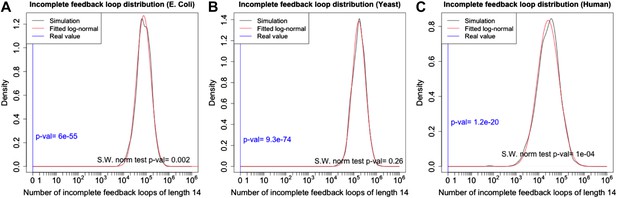
p-Value estimation for the number of long incomplete feedback loops.
The distribution of the number of long incomplete feedback loops in random graphs has the same structure as the number of feedback loops and the same arguments apply (See the caption of Figure 2—figure supplement 2). The distributions in E. coli (A), yeast (B), and human (C) are plotted using the same conventions of Figure 2—figure supplement 2.
Figure 3—figure supplement 3
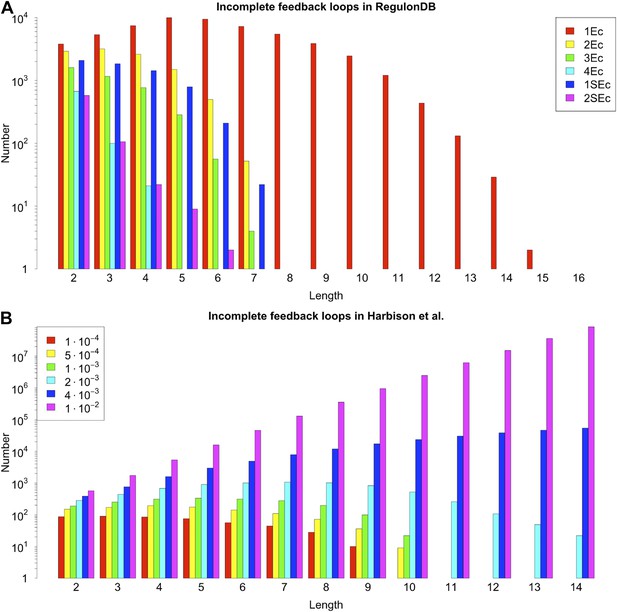
Number of incomplete feedback loops in the RegulonDB (E. coli) and Harbison et al. (yeast) datasets under different statistical conditions.
The number of incomplete feedback loops in E. coli (A) and yeast (B) remain stable under reasonable variation of the conditions used to construct the GRNs. See the caption of Figure 2—figure supplement 3 for the description of the different conditions associated with the network reconstruction. Note the logarithmic scale and the same phase shift observed in the feedback loop distribution (Figure 2—figure supplement 3).
Figure 3—figure supplement 4
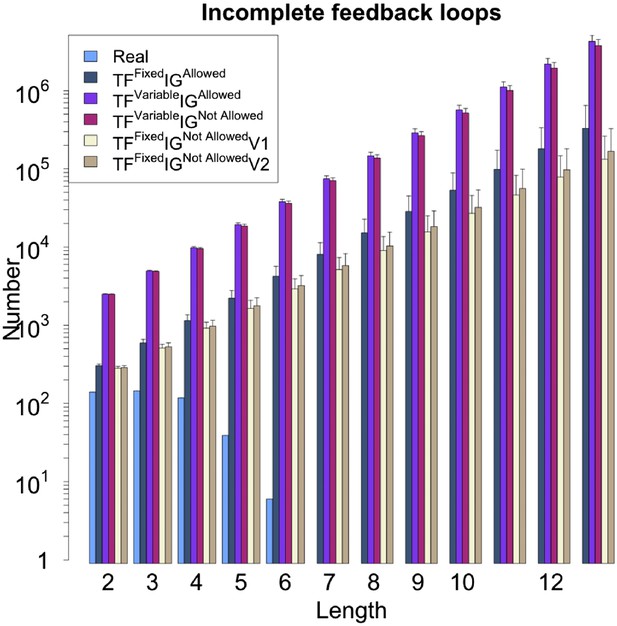
Number of feedback loops under different random models for RegulonDB (E. coli).
The different random models lead to different numbers of incomplete feedback loops. However, the same exponential growth is observable in all the models, in striking contrast to the real data. Note the logarithmic scale.
Figure 3—figure supplement 5
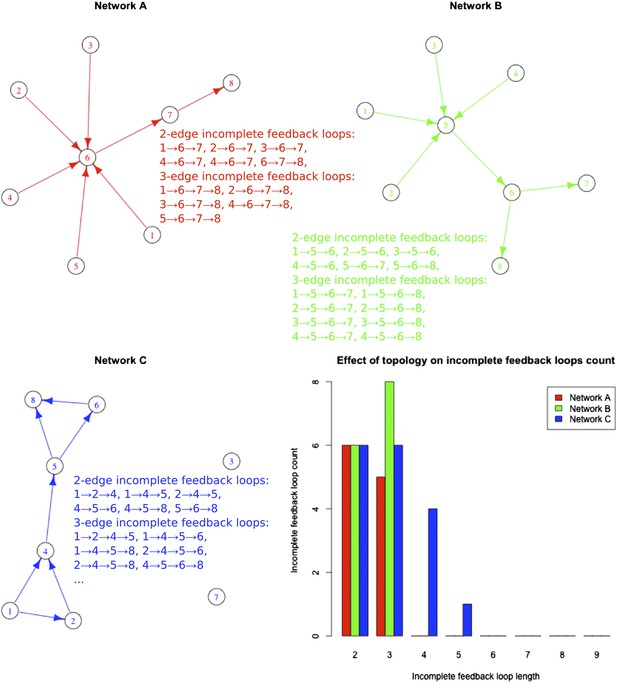
Incomplete feedback loop distribution in different networks.
The number of incomplete feedback loops is reported for different networks with the same number of edges. All the incomplete feedback loops of length two and three are reported for the network considered with matching colours. Note how the number of three-edge incomplete feedback loops is smaller, equal or larger than the number of two-edge incomplete feedback loops depending on the structure of the network considered.
Figure 4 with 4 supplements
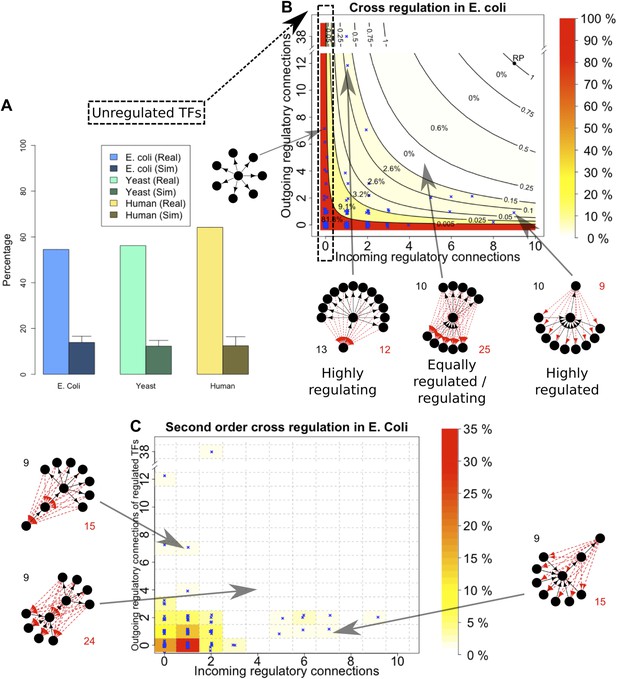
Evidence for BQS from TF regulation.
(A) For each organism, the percentage of TFs which are not regulated by any other TF is shown. Comparisons are made to randomly simulated networks containing the same number of genes, TFs, and connections. (B) Each of the 154 TFs in the E. coli GRN is plotted in the space of incoming regulatory connections (number of regulatory links from other TFs) and outgoing regulatory connections (number of regulatory links to other TFs). Solid lines indicate isoclines of relative probability (normalized to unity at reference point RP) for creating a 3-gene feedback loop under random addition of a link. Percentages and colours indicate the fraction of TFs within each band demarcated by isoclines. (C) Each of the 154 TFs in the E. coli GRN is plotted in the space of incoming regulatory connections (number of regulatory links from other TFs) and outgoing regulatory connections of regulated TFs (number of regulatory links originating from a TF that is regulated by the selected TF). In (B and C), schematic motifs are provided; black solid arrows indicate the motif, while red dashed arrows indicate potential arrows whose addition results in the formation of long feedback loops. For each motif, the number of actual arrows is indicated in black and the number of potential destabilising arrows is indicated in red.
Figure 4—figure supplement 1
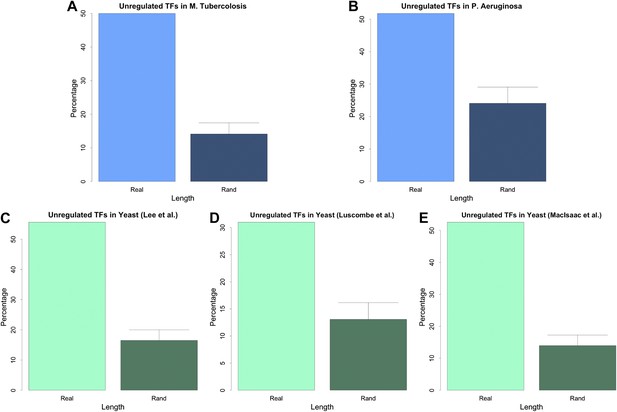
Unregulated TFs in P. aeruginosa, M. tuberculosis and other yeast datasets.
Percentage of unregulated TFs for M. tuberculosis (A), P. aeruginosa (B), the yeast dataset derived from Lee et al. (2002) (C), the yeast dataset derived from Luscombe et al. (2004) (D), and the yeast dataset derived from MacIsaac et al. (2006) (E). In each case the real dataset is compared with a randomly simulated network containing the same number of genes, TFs and connections. For the random networks, each graph reports the mean and standard deviation. Note the statistically significant difference of real and random data in all the dataset considered.
Figure 4—figure supplement 2
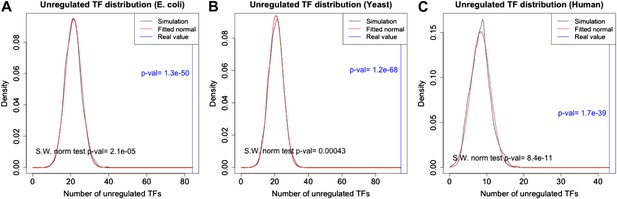
p-Value estimation for the number of unregulated TFs.
The distribution of the number of unregulated TFs in random graphs follows a normal distribution in E. coli (A), yeast (B) and human (C). See Figure 2—figure supplement 2, for the conventions used in the plots. Note the very small p-vals.
Figure 4—figure supplement 3
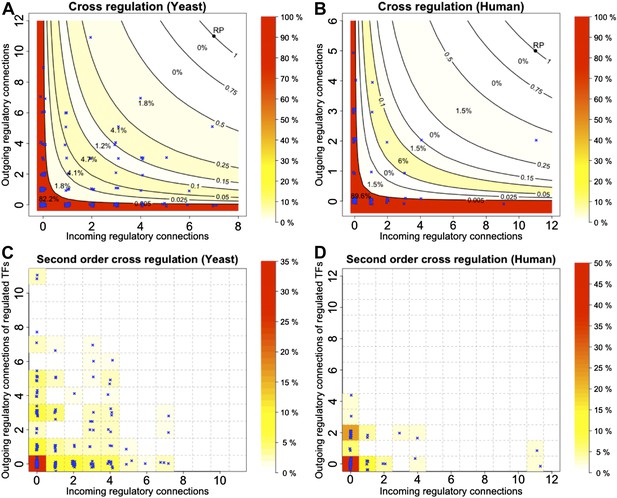
Cross regulation and second-order cross regulation in yeast and human.
(A and B) TF cross regulation in yeast and the human GM12878 cell lines. (C and D) Second-order cross regulation control for the same datasets. See the caption of Figure 4 for the conventions used in the plots.
Figure 4—figure supplement 4
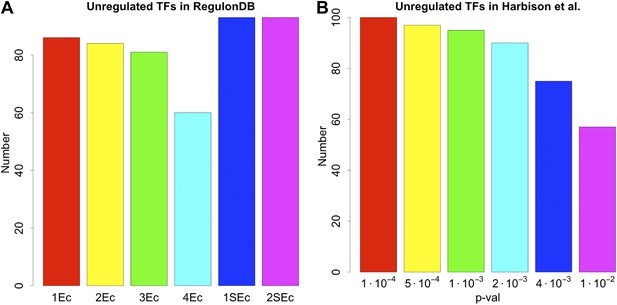
Number of unregulated TFs in the RegulonDB (E. coli) and Harbison et al. (2004) (yeast) dataset under different statistical conditions.
The number of unregulated TFs in E. coli (A) and yeast (B) remain very high regardless of the conditions used to construct the GRNs, supporting the strong embedding of this feature in the GRNs. See the caption of Figure 2—figure supplement 3 for the description of the different conditions associated with the network reconstruction.
Figure 5 with 4 supplements
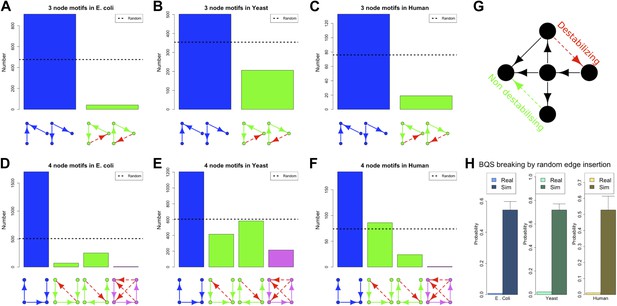
BQS in selected 3- and 4-gene motifs.
Count of 3- and 4-gene motifs in the GRNs of E. coli (A and D), S. cerevisiae (B and E), and human GM12878 cell line (C and F) are classified into different categories. The y-axis reports the number of motifs plotted under each bar using blue (buffered), green (mono-unbuffered) or violet (poly-unbuffered) solid arrows. Red dashed arrows are not part of the motifs but indicate the additional links that would create a 3- or 4-gene feedback loop. The motifs selected have an equal probability of occurrence in a random network (See also Figure 5—figure supplement 4B,E,F,H,K,L). Horizontal black dotted lines in panels A–F indicate the motif abundance expected in random networks. (G) In the network schematic indicated by black arrows, adding a new connection can affect BQS; certain arrows will create a long feedback loop (red dashed arrow), while others will not (green dashed arrow). (H) Probability that a random edge addition between TFs would result in the creation of a long feedback loop is reported compared to random simulations. The different values observed in the simulations are due to the different number of TFs and regulatory connections in the three organisms.
Figure 5—figure supplement 1
Labelling conventions for Figure Supplements.
To simplify the structure of Figure 5—figure supplements 2–4, the motifs are indicated by an IDs instead of being depicted graphically. These IDs are described here.
Figure 5—figure supplement 2
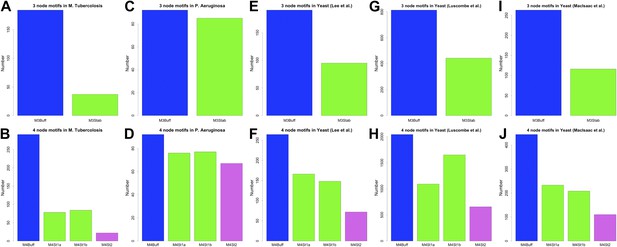
3- and 4-gene motifs in P. aeruginosa, M. tuberculosis and other yeast datasets.
Number of selected 3- and 4-gene motifs for M. tuberculosis (A and B), P. aeruginosa (C and D), the yeast dataset derived from Lee et al. (2002) (E and F), the yeast dataset derived from Luscombe et al. (2004) (G and H), and the yeast dataset derived from MacIsaac et al. (2006) (I and J). Note how the predictions of BQS are verified in all the datasets.
Figure 5—figure supplement 3
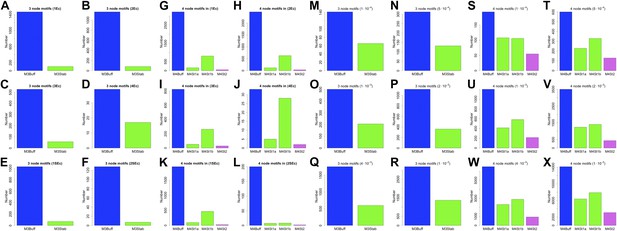
3- and 4-gene motifs in the RegulonDB (E. coli) and Harbison et al. (2004) (yeast) datasets under different statistical conditions.
The number of selected 3- and 4-gene motifs in E. coli (A–L) and yeast (M–X) follows the distribution predicted by BQS under all the conditions considered. This result supports the strong robustness of this analysis to noise.
Figure 5—figure supplement 4
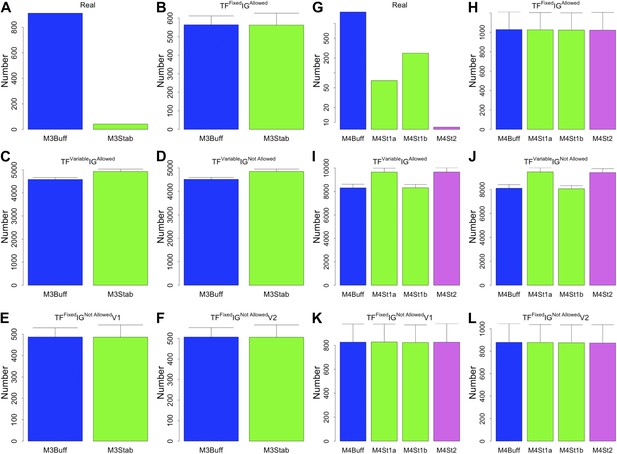
3- and 4-gene motifs under different random models for RegulonDB (E. coli).
As expected from theoretical considerations, when the number of TFs is fixed, the 3- and 4-gene motifs considered are equi-probable (B, E, F, H, K, and L). This equal probability is broken when the number of TFs is allowed to vary freely, as a consequence of the variable size of the TF-only network. However, this type of randomness limits, rather than increases, the number of buffered stable motifs, in striking contrast to the real data (A, C, D, G, I, and J).
Figure 6 with 3 supplements
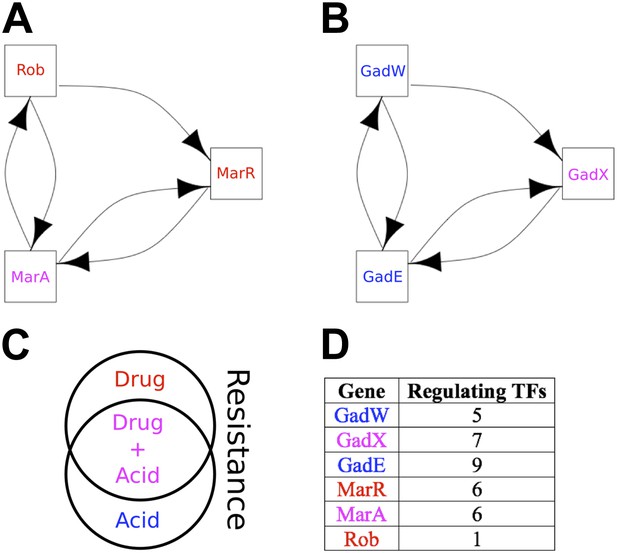
The two ‘illegal’ feedback loops in E. coli.
The figure shows connections between TFs in the two motifs in E. coli that contain feedback loops with >2 links (A and B). Note the common feature of two adjacent 2-gene feedback loops. (C) Colours indicate if a gene is implicated in drug resistance (red), acid resistance (blue), or both (violet). (D) The number of regulatory connections for each TF in (A and B).
Figure 6—figure supplement 1
The transcription factor GRN in E. coli with long feedback loops highlighted.
The TFs implicated in the formation of the two motifs illustrated in Figure 6 are coloured in black and their interactions in red. All the other TF are coloured in grey and their interactions in blue.
Figure 6—figure supplement 2
Long feedback loops in M. tuberculosis.
Only three long feedback loops are observed in M. tuberculosis (A–C). Note the presence of the same 3-node motifs observed in E. coli (Figure 6A,B) and how these two motifs are entangled in the four node feedback loop (C).
Figure 6—figure supplement 3
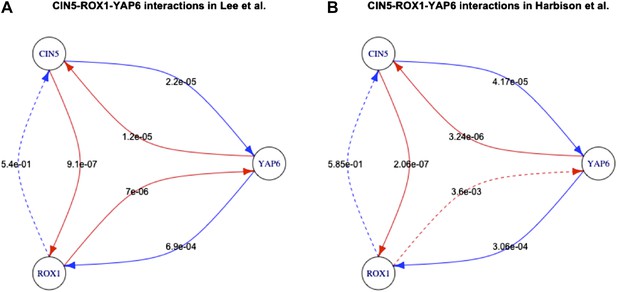
Long feedback loops in Lee et al. (yeast).
Only one long feedback loop is observed in the yeast dataset derived by Lee et al. (A). Since Harbison et al. (2004) uses a technology similar to Lee et al. (2002) and can be considered to have provided an updated version of the network, we analysed what caused the disappearance of the invalid loop reported by Lee et al. (2002). Five of the six interactions have comparable p-values in the two datasets (A and B). However, the p-value for the interaction between ROX1 and YAP6 changes by three orders of magnitude, thus transforming the feedback loop into a feedforward loop that is consistent with BQS. This observation indicates how the strong predictions of BQS can be used to identify potential inaccuracies and problems in GRN data.
Figure 7 with 3 supplements
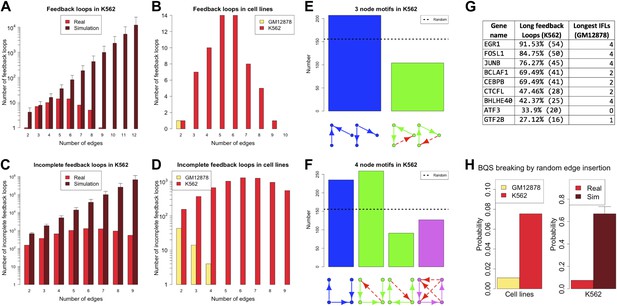
Broken BQS in a human cancer cell line.
(A and C) Number of feedback loops and incomplete feedback loops in the GRN of the human cancer cell line K562, compared to the corresponding random network. Data is provided on a logarithmic scale. (B and D) Number of feedback loops and incomplete feedback loops in the GRN of K562, compared to the human non-cancer cell line GM12878. Note the use of a linear scale in (B). (E and F) Motif analysis of BQS for K562 for 3- and 4-gene motifs, using the same convention as described in Figure 5. (G) Genes implicated in the formation of long feedback loops in K562 are reported with the number and percentage of loop created, the length of the longest incomplete feedback loops involving the gene in GM12878 are also indicated. (H) The probability that a random edge addition would result in the creation of a long feedback loop is reported for both GM12878 vs K562 and K562 vs randomly simulated networks containing the same number of nodes and connections. Note that the GRNs of GM12878 and K562 have similar link densities. They comprise 4071 and 4049 genes respectively, and 8466 and 11,707 regulatory connections respectively.
Figure 7—figure supplement 1
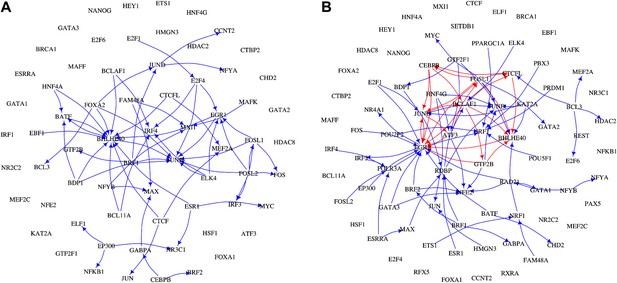
The transcription factor GRNs for GM12878 and K562.
TFs and their interactions are plotted for the non-cancer cell line GM12878 (A) and the leukaemia cell line K562 (B). TF names are indicated in black, transcriptional interactions implicated in the formation of long feedback loops are coloured in red, while all the other interactions are coloured in blue.
Figure 7—figure supplement 2
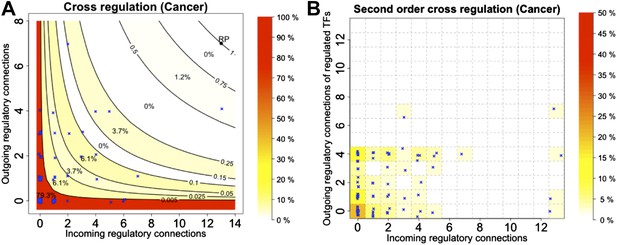
Cross regulation and second-order cross regulation in cancer.
TF cross regulation (A) and second-order cross regulation (B) display in cancer similar overall trend when compared to E. coli, yeast and the non-cancer cell line (Figure 4, Figure 4—figure supplement 3). However, a slightly less stringent distribution can be observed, compatible with a diminished stability.
Figure 7—figure supplement 3
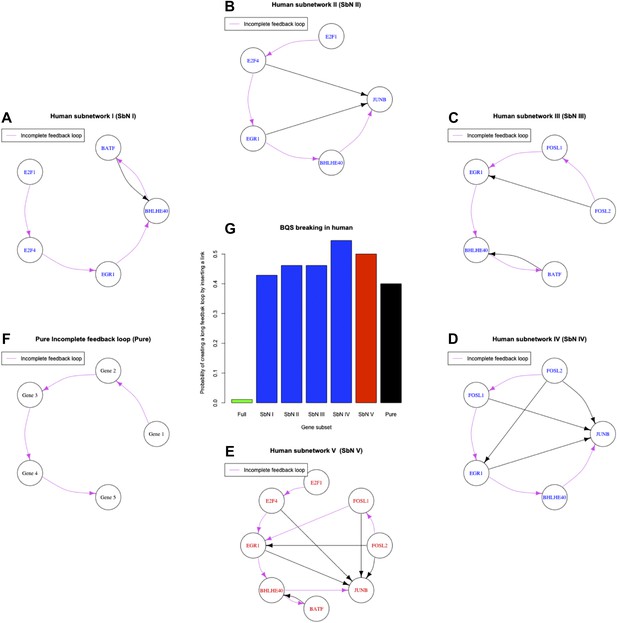
Longest incomplete feedback loops in the GM12878 GRN and their destabilization potential.
The smallest subset of genes containing the longest incomplete feedback loops of the GRN of the human cell line GM12878 are illustrated (A–D). Along with the smallest subset of genes containing all longest incomplete feedback loops of the GM12878 GRN (E) and the simplest 5-gene incomplete feedback loop (F). The probability that inserting a random edge will introduce a long feedback loop in the human transcription factor networks (green bar), in the sub networks identified by the single incomplete feedback loops (blue bars), in the sub network identified by all the incomplete feedback loops (red bar), and in a pure incomplete feedback loop (black bar) is also displayed (G). Note how the probability increases drastically as incomplete feedback loops are considered.
Figure 8 with 1 supplement
BQS in homeostatic murine dendritic cells.
(A and B) Number of feedback loops and incomplete feedback loops compared to the corresponding random network. Data is provided on a logarithmic scale. (C and D) Motif analysis of BQS for 3- and 4-gene motifs, using the same convention as described in Figure 5. (E) Percentage of TFs which do not regulate other TFs compared to the corresponding random network. (F) Relation between the number of incoming and outgoing regulatory connections; the same conventions of Figure 4B are used.
Figure 8—figure supplement 1
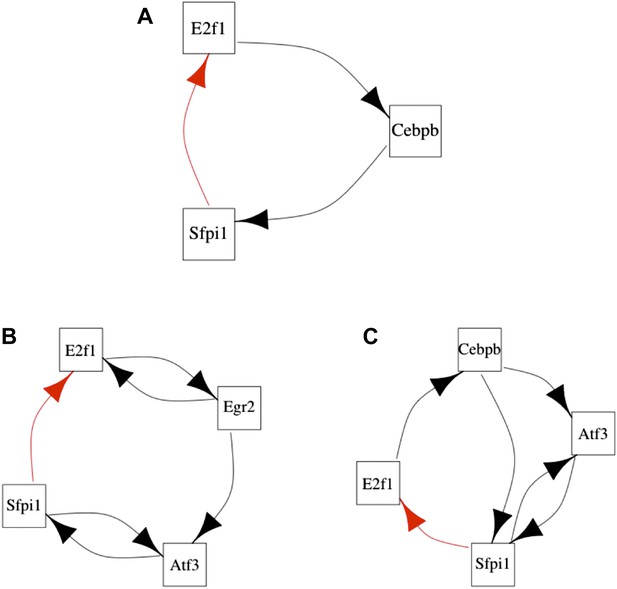
Long feedback loops in the GRN of homeostatic dendritic cells.
Three long feedback loops can be found in the GRN of homeostatic dendritic cells (A–C). However, all of them depend critically on the transcriptional interaction between Sfpi1 and E2f1. The interaction between Sfpi1 and E2f1 is highlighted in red for clarity. Note that such an interaction is the only one that is fundamental for the formation of all the long feedback loops.
Figure 9 with 1 supplement
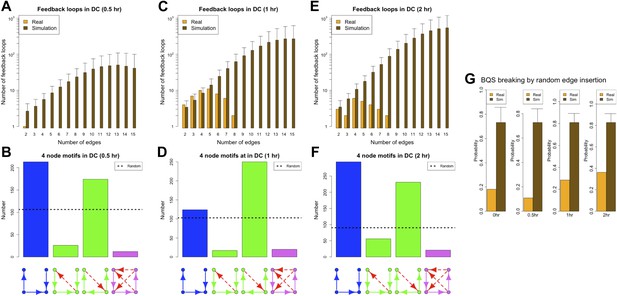
BQS during a transcriptional program activation in dendritic cells.
(A, C and E) Number of feedback loops and incomplete feedback loops in the GRN of dendritic cells at different times after a stimulus compared to the corresponding random network. Data is provided on a logarithmic scale. (B, D and F) Motif analysis of BQS for 4-gene motifs, using the same convention as described in Figure 5. (G) Probability of creating additional long feedback loops by the addition of a random link between TFs in the GRN of dendritic cells at different times after a stimulus and the corresponding random network.
Figure 9—figure supplement 1
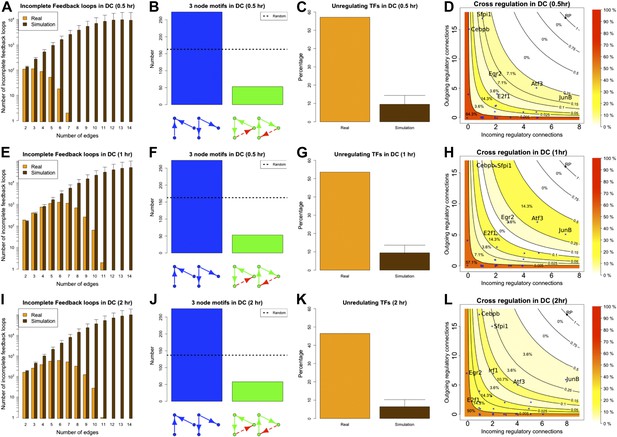
BQS in the GRN of dendritic cells.
As discussed in the main text, various degrees of stability can be observed in the GRN of dendritic cells when they are in the process of activating a new transcriptional program. The GRN is very stable 0.5 hr after the new transcriptional program has been initiated (A–D), it is unstable after 1 hr (E–H), but partially stabilizes after 2 hr (I–L). The comparison of (D, H and L) indicates that a change in the balance between the number of inputs and outputs of a few TFs plays a strong role in controlling the stability of the GRN. To provide a better understanding of the dynamics, in (D, H and L), the TFs with the most unbalanced input/output are labelled. Looking at the labelled TFs it is possible to notice how they tend to move towards the centre of the plot in panel H and move back to the sides in (L).
Figure 10
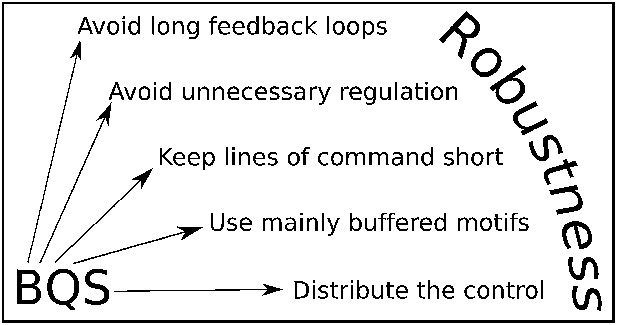
BQS Rules.
BQS provides five general design principles applicable to any regulatory system. The rules are described in more detail in the ‘Discussion’ Section.
Tables
Table 1
Basic network properties for all the genome-wide GRNs used in the article
| Organism | Nodes (F) | Edges (F) | Nodes (T) | Edges (T) | Density (F) | Density (T) |
|---|---|---|---|---|---|---|
| E. coli | 1470 | 2909 | 154 | 140 | 0.0013 | 0.0059 |
| M. tuberculosis | 1624 | 3169 | 82 | 85 | 0.0012 | 0.013 |
| P. Aeruginosa | 692 | 991 | 85 | 81 | 0.0021 | 0.011 |
| Yeast (Lee) | 2417 | 4348 | 106 | 96 | 0.00074 | 0.0086 |
| Yeast (Harbison) | 2933 | 6152 | 169 | 188 | 0.00071 | 0.0066 |
| Yeast (Luscombe) | 3459 | 7053 | 142 | 254 | 0.00059 | 0.013 |
| Yeast (MacIsaac) | 2079 | 4097 | 116 | 134 | 0.00095 | 0.010 |
| GM12878 | 4049 | 11,707 | 82 | 84 | 0.00071 | 0.013 |
| K562 | 4071 | 8466 | 67 | 59 | 0.00051 | 0.013 |
-
Except when stated otherwise, random networks were generated preserving the number of transcription factors, genes, and interactions for E. coli, P. aeruginosa, M. tuberculosis, yeast, and the human cell lines. Random networks generated by preserving additional topological properties were also considered (See the subection ‘Effect of different constraints on the generation of random networks’) and confirm the results discussed. For murine dendritic cells, random networks were constructed by preserving the number of transcription factors and interactions among them. Note that consequently the number of feedback loops and incomplete feedback loops is an underestimate with respect to the data considered in the other random networks. Self-regulating interactions were ignored. Since genes not encoding for TFs do not regulate other genes, a full-network analysis would artificially increase the stability property of the network. Therefore, to limit the bias introduced by the limited number of transcription factors, the number of incomplete loops, the motif abundance, the number of regulatory connections, and the probability of adding additional long feedback loops when a new regulatory connection is inserted were computed considering only the interactions among transcription factors. For each different type of random network, 1000 instances were generated for the data presented in the main Figures, while 100 instances were generated for the data presented in the Figure Supplements.
Table 2
Properties of the different random models used
| Model name | # of genes | # of interactions | # of TFs | Isolated genes |
|---|---|---|---|---|
| TFVariableIGAllowed | Fixed | Fixed | Variable | Allowed |
| TFFixedIGAllowed | Fixed | Fixed | Fixed | Allowed |
| TFVariableIGNot Allowed | Fixed | Fixed | Variable | Not allowed |
| TFFixedIGNot AllowedV1 | Fixed | Fixed | Fixed | Not allowed |
| TFFixedIGNot AllowedV2 | Fixed | Fixed | Fixed | Not allowed |
Table 3
Functions used to produce the different random networks
| Model name | Function used |
|---|---|
| TFVariableIGAllowed | GenerateRandomNetwork.IG.Allowed() |
| TFFixedIGAllowed | GenerateRandomNetwork.IG.Allowed() |
| TFVariableIGNot Allowed | GenerateRandomNetwork.IG.NotAllowed.V1() |
| TFFixedIGNot AllowedV1 | GenerateRandomNetwork.IG.NotAllowed.V1() |
| TFFixedIGNot AllowedV2 | GenerateRandomNetwork.IG.NotAllowed.V2() |
Additional files
-
Supplementary file 1
Edges that result in the formation of at least one long feedback loop when inserted in the GM12878 GRN. The number of long feedback loops created and the length of the longest feedback loops are also indicated. Supplementary file 1 lists all the 48 edge insertions that result in the creation of long feedback loops when inserted in the GM12878 GRN. Note the high participation of JUNB and BATF as sources and of FOSL1/2 as targets. Three of these destabilizing interactions are actually observed in the K562 cancer cell line: from JUNB to BCLAF1, from BATF to EGR1, and from JUNB to EGR1. These interactions are highlighted in a bold character. The GRN of the GM12878 cell line contains 67 TFs and 59 interactions among them. Since in a network with 67 nodes there are 67*(67-1) = 4422 possible directed links with different source and targets, 4422-59 = 4362 additional regulations can be inserted between the TFs in the GM12878 GRN. Four regulatory connections between TFs are observed both in GM12878 and in K562: BCLAF1–> BHLHE40, CTCFL–> BHLHE40, EGR1–> JUNB, FOSL1–> JUNB. Of all the potential additional regulatory connections among the TFs of the GM12878 cell line, 56 are observed in the K562. Therefore, the likelihood of observing in K562 one of the 4362 potential regulations of GM12878 is 56/4362 ≈ 0.013. The likelihood of observing in K562 one of the potentially destabilising regulations of GM12878 is 3/48 = 0.062. Finally, two of the potentially destabilising interactions of the GM12878 have a particularly strong destabilization potential: an additional transcriptional regulation from JUNB to FOSL2 will create five long feedback loops and an additional transcriptional regulation from JUNB to E2F1 will create 3. Once again, our analysis highlights genes that may play a key role in cancer progression (Kouzarides and Ziff, 1989; Engelmann and Pützer, 2012).
- https://doi.org/10.7554/eLife.02863.041
-
Source code 1
R Functions used to generate the random networks, to count the number of feedback loops, and to count the number of incomplete feedback loops.
- https://doi.org/10.7554/eLife.02863.042
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Buffered Qualitative Stability explains the robustness and evolvability of transcriptional networks
eLife 3:e02863.
https://doi.org/10.7554/eLife.02863
