Independent theta phase coding accounts for CA1 population sequences and enables flexible remapping
- University of Edinburgh, United Kingdom
Figures
Figure 1
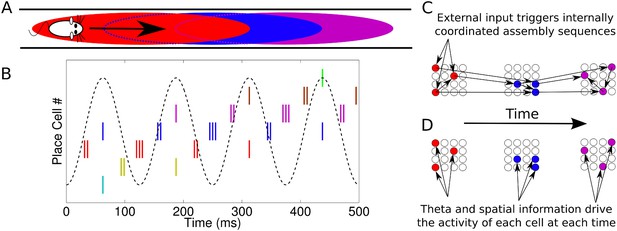
Phase sequences in a place cell population.
(A) During navigation, place cells are sequentially activated along a route. (B) Within each theta cycle, this slow behavioral sequence of place cell activations is played out on a compressed timescale as a theta sequence. Theta sequences involve both rate and phase modulation of individual cells, but it remains unclear whether additional coordination between cells is present. (C) Internal coordination may bind CA1 cells into assemblies, and sequential assemblies may be chained together synaptically. This would require specific inter- and intra-assembly patterns of synaptic connectivity within the network. (D) Alternatively, according to the independent coding hypothesis, each cell is governed by theta phase precession without additional coordination.
Figure 2 with 1 supplement
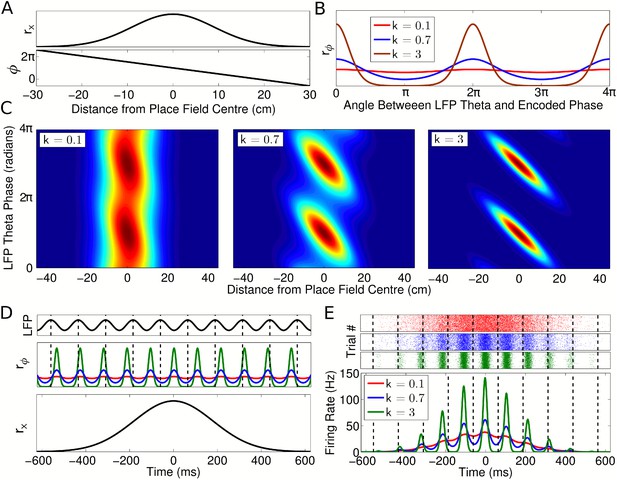
Single cell coding model.
(A) Firing rate and phase at different locations within a cell's place field are determined by a Gaussian tuning curve rx and linearly precessing encoded phase ϕ, respectively. (B) The dependence of single cell activity on the LFP theta phase θ is modeled by a second tuning curve rϕ which depends on the angle between the LFP theta phase θ and encoded phase ϕ at the animal's location. The phase locking parameter k controls the precision of the phase code. (C) The combined dependence of single cell activity on location and LFP theta phase. (D) Temporal evolution of the rate and phase tuning curves for a single cell as a rat passes through the place field at constant speed. (E) The total firing rate corresponding to (D), and spiking activity on 1000 identical runs.
Figure 2—figure supplement 1
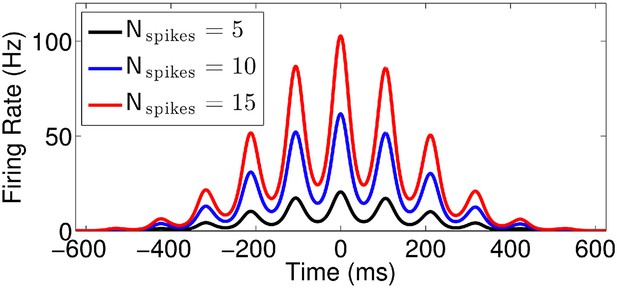
Effect of normalization factor (Nspikes).
Firing rate vs time for runs with v = 50 cm/s, k = 0.7, and three different values of Nspikes.
Figure 3 with 1 supplement
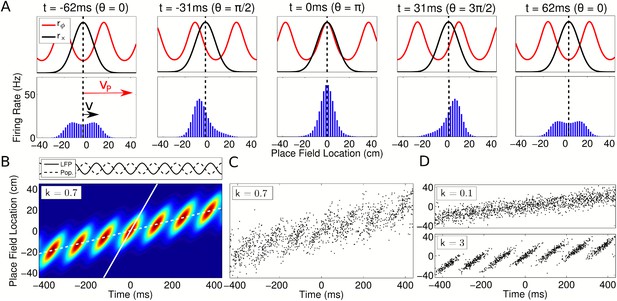
Spatiotemporal dynamics of CA1 populations governed by independent coding.
(A) Top: Population dynamics during a single theta cycle on a linear track after ordering cells according to their place field center xc in physical space. The two components of the population activity are shown—the slow moving envelope (black) and the fast moving traveling wave (red), which give rise to rate coding and phase coding, respectively (cf. Figure 2). Bottom: Resulting firing rates across the population. When the traveling wave and envelope are aligned, the population activity is highest (middle panel). The dashed line shows the location of the rat at each instant. (B) Firing rate in the population over seven consecutive theta cycles. The fast and slow slopes are shown (solid and dashed lines, respectively), corresponding to the speeds of the traveling wave and envelope as shown in part (A). The top panel shows the LFP theta oscillations and emergent population theta oscillations, which are generated by the changing population activity as the traveling wave shifts in phase relative to the slower envelope (see Video 1). (C and D) The spiking activity for a population of 180 cells. All panels used v = 50 cm/s, so that vp = 350 cm/s and c = 7.
Figure 3—figure supplement 1
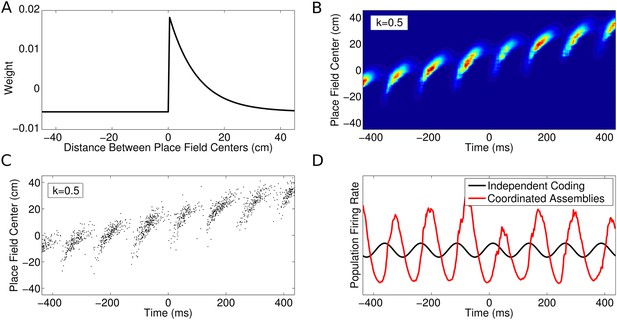
CA1 population activity governed by coordinated assemblies.
(A) The simulated place cells interact via a combination of asymmetric excitation and feedback inhibition. The weights plotted here govern how the spikes emitted by a given cell will influence the spiking activity of its peers depending on their relative place field locations. (B) Population firing rate on a single run along a linear track (180 cells with v = 50 cm/s and k = 0.5). The firing rate in each cell is a product of the animal's location, the LFP theta phase and the influence of recent peer spiking activity. (C) The spiking activity, generated using an inhomogeneous Poisson process. (D) Comparison of the global population firing rate for an independent coding population (black) and a coordinated population (red), with identical single cell properties. Interactions between cells amplify theta oscillations and introduce a shift in firing phase.
Figure 4 with 2 supplements
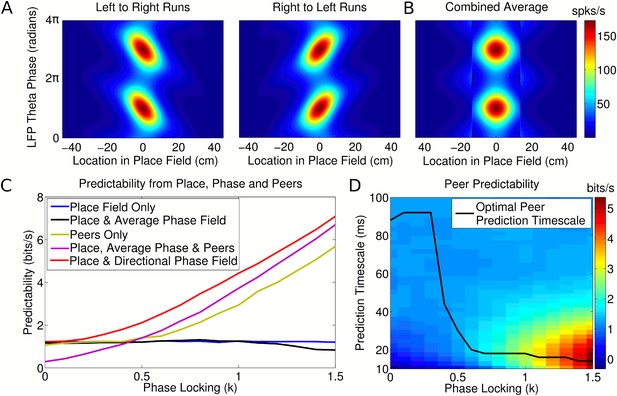
Peer prediction analysis for an independent population code.
(A) Combined place and phase fields constructed from simulated data using only runs with a single direction. (B) Place/phase field constructed from a combination of both running directions, as used by Harris et al. (2003). (C) Predictability analysis, using various combinations of place, phase, and peer activity. When using the nondirectional phase field of Harris et al. (2003), an additional peer predictability emerges (black vs green and purple). However, this additional predictability is seen to be erroneous if the directional phase field is used to predict activity (red). (D) Dependence of peer predictability on the peer prediction timescale and phase locking of individual cells, for an independent population code. The heat map shows the predictability of a cell's activity from peer activity (cf. part C, green line). The optimal peer prediction timescale depends on the amount of phase locking. The 20 ms characteristic timescale of peer correlations reflects independent phase precession of single cells rather than transient gamma synchronization of cell assemblies.
Figure 4—figure supplement 1
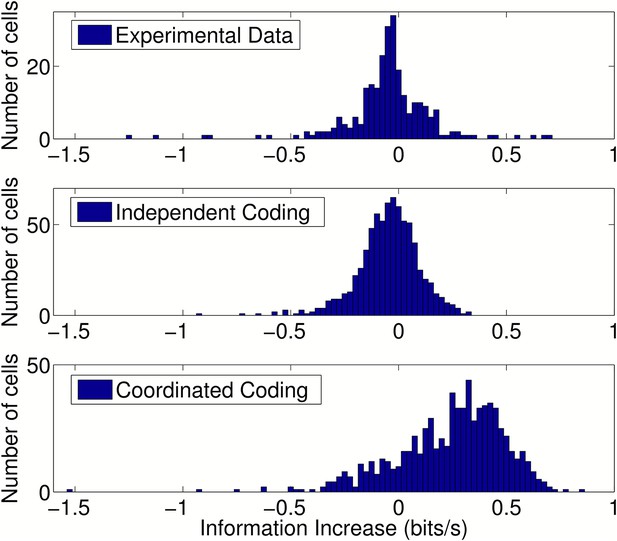
Change in information after addition of peer activity to prediction metrics.
Distributions of information gain/loss in individual cells after including peer activity in addition to all other prediction metrics. For independent coding and experimental data, peer prediction causes a decrease in information on average (p = 3.9 × 10−17 and p = 1.4 × 10−6, respectively). For coordinated coding, peer prediction causes an increase in information on average (p = 9 × 10−83). The decrease in information observed for independent coding simulations when peer activity is included occurs due to overfitting on a dataset of finite size. Due to statistical fluctuations in the data, peer weights are generally estimated as non-zero. Both the peer weights and the change in information when peers are included would be expected to approach zero as the amount of data increases for independent coding simulations, but not for coordinated coding simulations.
Figure 4—figure supplement 2
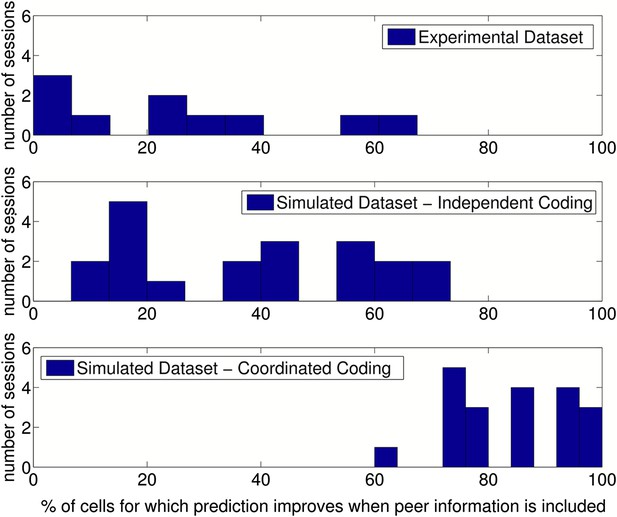
Results of prediction analysis on individual sessions.
Top: Number of cells for which prediction improved with peers after place fields, velocity modulation factors and directional phase fields had been fitted, shown for each session/running direction in the experimental dataset. Middle: The results when the same analysis was applied to data simulated with independent coding (twice as many sessions were simulated for comparison). Bottom: The results when data were simulated with coordinated assemblies.
Figure 5 with 2 supplements
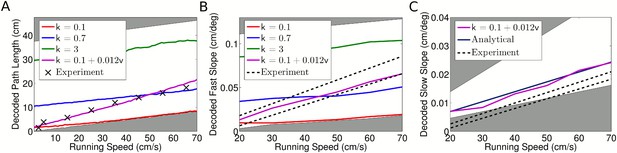
Decoded sequence path lengths and population activity propagation speeds.
(A) With constant phase locking, the decoded path length increases linearly with running speed, but to account for experimental data a dependence of phase locking on running speed is required. The shaded regions show lower and upper bounds (k = 0 and k = ∞). (B) Dependence of decoded fast slope on running speed (cf. our Figure 3B; Figure 3 of Maurer et al. (2012)). Again, a match to the data requires a velocity dependent phase locking. (C) The decoded slow slope matches the analytical value, where the population travels at the running speed v. Bounds show LFP theta frequencies below 4 Hz (upper bound) and above 12 Hz (lower bound) at each given running speed.
Figure 5—figure supplement 1
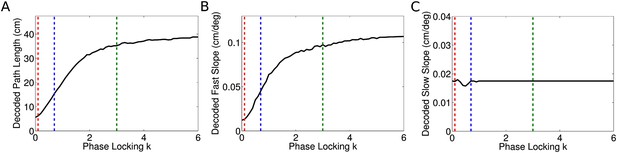
Dependence of decoded sequence path lengths, fast slopes, and slow slopes on phase locking.
(A) The decoded path length depends on the phase locking of individual cells. For zero phase locking, the decoded path length is the distance traveled by the rat in a theta cycle. This is because the decoded location in each time bin is simply the location of the rat. As phase locking is increased the path length increases asymptotically towards our analytical result, which is the distance traveled by the rat plus one full place field. This effect arises due to the gradual separation of cells representing different locations into separate theta phases, as seen explicitly in Figure 3C,D. Phases within a single theta cycle represent past, present, and future locations along the track. Dashed lines show the phase locking values plotted in Figures 2, 3. (B) Dependence of decoded fast slope on phase locking. While the analytical result for vp is independent of phase locking, the decoded value shown here is consistent with the intuitive notion that the sequence path length D is equal to the distance traveled by the fast moving wave in a theta cycle. (C) The decoded slow slope does not depend on phase locking, which is expected given the separation of timescales involved.
Figure 5—figure supplement 2
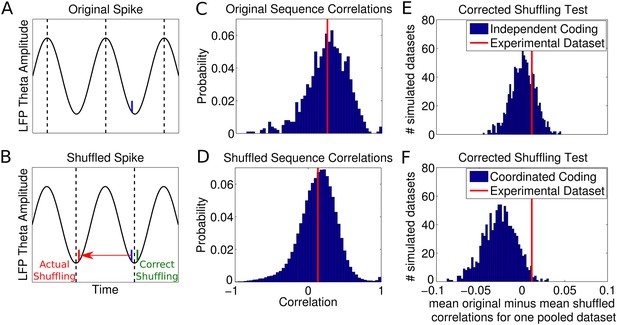
Results of shuffling analysis.
(A–D) The analysis of Foster and Wilson (2007) and (E–F) a corrected analysis. (A) Spike phases were initially calculated by interpolation between theta peaks, shown as dotted lines. (B) After shuffling the phases of spikes, a new spike time is calculated by interpolation between the nearest two theta troughs (dotted lines) to the original spike, which often generates erroneous spike times. The shuffled spike in this case acquires a small phase jitter, but a large temporal jitter. (C) The unshuffled sequence correlations between cell rank order and spike times. The red line shows the mean correlation. (D) Shuffled sequence correlations remained greater than zero, but were significantly reduced relative to the unshuffled case as in experimental data (Foster and Wilson, 2007). (E) Results of a corrected shuffling procedure applied to simulated independent coding datasets and an experimental dataset (height magnified for comparison). Displayed are the average changes in sequence correlations caused by shuffling for each simulated dataset. In 74% of simulated datasets, there was no significant difference between the original and shuffled distributions. (F) Results of the corrected shuffling procedure when applied to datasets simulated with coordinated assemblies. In 81% of simulated coordinated coding datasets, shuffling significantly changed the distribution of sequence correlations. The experimental dataset was not significantly affected by shuffling (p = 0.28, t-test, 2436 putative sequences).
Figure 6 with 1 supplement
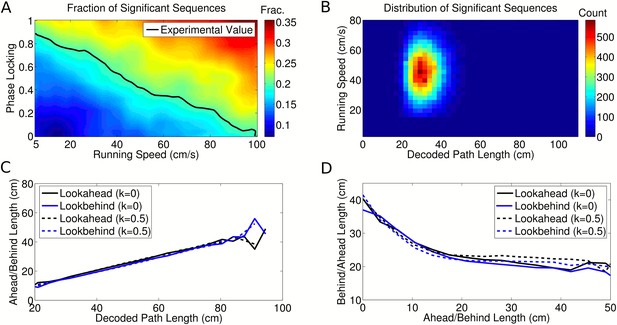
Analysis of individual sequence statistics.
(A) The fraction of theta cycles which are classified as ‘significant sequences’ according to the Gupta et al. (2012) analysis, as a function of running speed and phase locking (for simulated data generated under the independent coding model). Large fractions of significant sequences are generated even without phase coding or theta sequences within the population (i.e., at k = 0). The black line shows the fraction reported experimentally. (B) The distribution of significant sequences over running speed and decoded path length for simulated data with phase locking k = 0.5, as calculated by Gupta et al. (2012) (cf. their Figure 1c). (C) The relationship between decoded path length and decoded ahead and behind lengths for significant sequences, calculated for a dataset with no theta activity (k = 0) and a dataset with realistic theta activity (k = 0.5). (D) The relationship between the ahead length of the sequence and the behind length of the sequence for these two datasets. Note that the properties of the decoded trajectories do not depend on the theta activity in the data. This replicates the experimental data (cf. Figure 4a-c of Gupta et al. (2012)), showing that similar trajectories are decoded by this algorithm regardless of the presence of theta sequences.
Figure 6—figure supplement 1
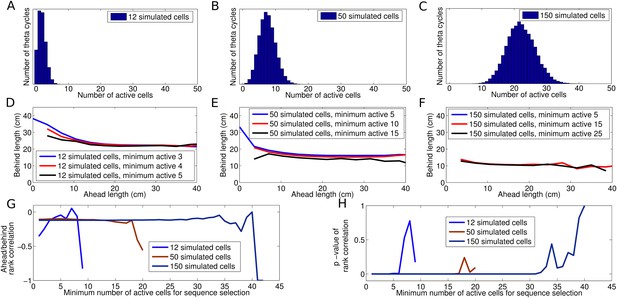
Dependence of decoded trajectories on the number of cells in a sequence.
(A–C) Distributions of the number of cells which spike in a theta cycle, for simulations of the independent coding model with different densities of place fields on the track (i.e., different numbers of place fields on a track of fixed length). (A) The cell density used to reproduce the results of Gupta et al. (2012). (B and C) Simulations with higher place field densities in which more active cells are recorded in each theta cycle on average. (D–F) Relationship between decoded ahead and behind length, calculated as in Gupta et al. (2012), shown for simulations with different place field densities and for different thresholds of the minimum number of cells required for a sequence to be included for analysis. (D) Simulations with 12 cells on the track and a threshold of three cells generate results similar to Gupta et al. (2012). (E–F) The density of place fields on the track and the threshold for sequence selection affect the decoded trajectories, with higher values for either resulting in a smaller change in behind length as a function of ahead length. (G–H) Spearman's rank correlation between ahead length and behind length for different place field densities plotted as a function of the threshold for the minimum number active of cells. Although the magnitude of the effect shown in (D–F) is diminished as these quantities increase, the correlation between ahead and behind length stays constant. Moreover, this correlation remains significant despite the decreasing effect size. Only when the number of selected sequences becomes too low to maintain a reliable measure does the effect become insignificant.
Figure 7 with 1 supplement
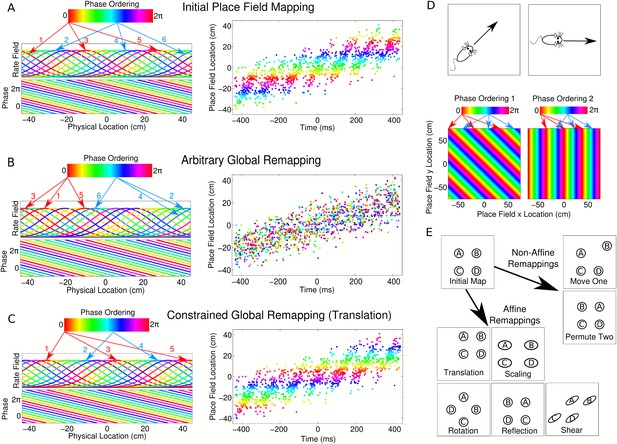
Properties of CA1 populations governed by linear phase coding.
(A) On a linear track, cells which precess linearly in phase maintain fixed theta phase lags. This is illustrated as a phase ordering (colored bar), which describes the relative phase of each cell (arrows show locations of cells at each phase). Each cell has a constant, running speed dependent frequency and a fixed phase offset to each other cell. (B) A complete global remapping with phase lags between cells held fixed. Theta sequences and population oscillations are abolished. (C) In a constrained place field remapping, theta sequences are preserved. (D) In open environments, phase lags depend on running direction. The set of population phase lag configurations needed to generate sequences in each direction is called a phase chart. (E) If a population has a fixed phase chart, the possible remappings are restricted to affine transformations.
Figure 7—figure supplement 1
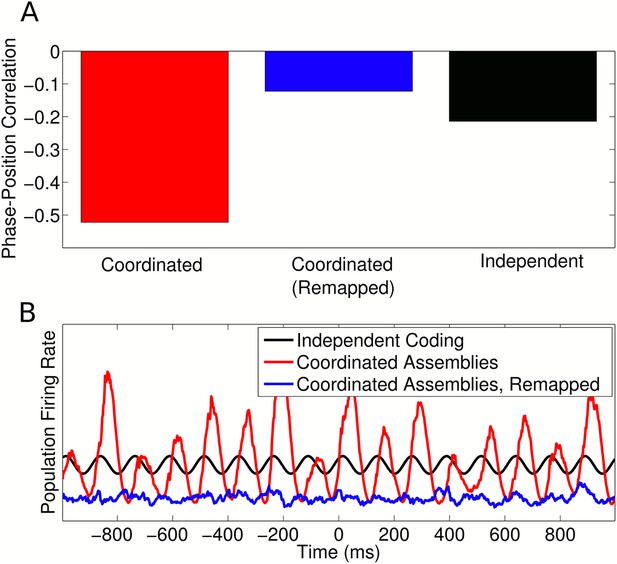
Remapping with coordinated assemblies.
(A) Comparison of single cell phase precession generated by coordinated assemblies (before and after remapping) and independent coding. For this simulation, single cell phase and rate fields were assumed to be perfectly remapped, so that any changes are purely due to assembly interactions. Note that, while assembly interactions improve phase coding in single cells in the initial environment, after remapping these same interactions disrupt phase precession and cause a lower (circular-linear) correlation between spike phase and animal location than that generated by independent cells. (B) Population firing rate on a single trial along a linear track. While assembly interactions initially entrain and amplify theta oscillations in the population compared to independent cells, after remapping these interactions disrupt theta activity and cause a lower overall activity level.
Figure 8
Properties of CA1 populations governed by sigmoidal phase coding.
(A–C) Firing rate and intracellular phase and frequency in the linear (dashed lines) and sigmoidal models (solid lines) during the crossing of a place field. In the sigmoidal model, phase precession is initiated inside the place field by an elevation of intracellular frequency from baseline. (D–F) Firing rate and intracellular phase and frequency for a place cell population on a linear track. In the sigmoidal model, an intracellular theta phase lag between cell pairs develops as the animal moves through their place fields. Outside their place fields, cell pairs are synchronized. (G) Global remapping in the linear and sigmoidal models. The sigmoidal model allows arbitrary remapping without disrupting population sequences.
Videos
Video 1
Traveling wave dynamics in populations of CA1 place cells.
Top: Distribution of the rate (black) and phasic (red) tuning curves for a population of linear phase coding place cells during constant speed locomotion on a linear track (cf. Figure 3A). The evolution in the population over 7 consecutive theta cycles is shown, slowed by a factor of approximately 16×. Bottom: The evolution of the overall firing rate distribution in the population, generated by multiplying the two tuning curves shown in the top panel. Note that the population firing rate undergoes oscillations at LFP theta frequency and the center of mass of the population activity shifts from behind the animal to ahead of the animal in each theta cycle.
Video 2
Population dynamics with sigmoidal phase coding.
Top: Distribution of the rate (black) and phasic (red) tuning curves for a population of sigmoidal phase coding place cells during constant speed locomotion on a linear track. Bottom: The evolution of the overall firing rate distribution in the population. Again, the population firing rate undergoes oscillations at LFP theta frequency and the center of mass of the population activity shifts from behind the animal to ahead of the animal in each theta cycle. However, in this case cells with place field centers distant from the animal's current location are synchronized with zero phase lag.
Tables
Table 1
Performance of prediction metrics on experimental and simulated data
| Prediction metric | Independent coding | Coordinated coding | Experimental data |
|---|---|---|---|
| Location | 100% | 100% | 44.6% (SEM 5.8%) |
| Running speed | 99.3% | 99.7% | 77.8% (SEM 3.7%) |
| Phase field | 99.3% | 100% | 75.7% (SEM 5.7%) |
| Peer activity | 38% | 84.3% | 32.5% (SEM 11%) |
-
The percentage of cells for which prediction performance increased with the addition of each metric. Percentages refer to the number of cells for which information increased when the specified metric was included in addition to those listed in rows above. Note that for velocity, phase and peer prediction, only those cells for which prediction performance improved with information about location were considered. Simulations demonstrate that, after taking into account place fields, velocity modulation factors and phase fields, information about peer activity improves prediction for the majority of cells when coordination is present, but not when cells are independent. Experimental data are consistent with independent coding.
Additional files
-
Supplementary file 1
Mathematical appendices. This file includes all mathematical methods and derivations pertaining to the models described in the main text.
- https://doi.org/10.7554/eLife.03542.022
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Independent theta phase coding accounts for CA1 population sequences and enables flexible remapping
eLife 4:e03542.
https://doi.org/10.7554/eLife.03542
