The evolution of non-reproductive workers in insect colonies with haplodiploid genetics
- Harvard University, United States
- Center for Mathematical Sciences and Applications, Harvard University, United States
- Emmanuel College, United States
Figures
Figure 1
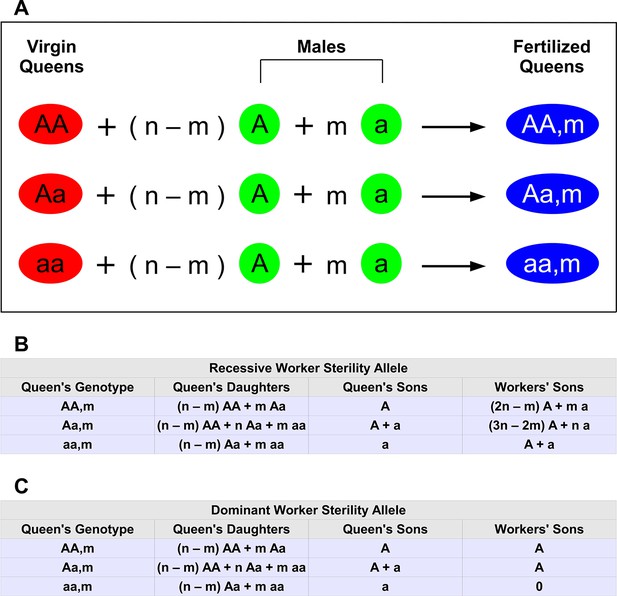
Haplodiploid genetics and multiple matings.
The wild-type allele is A. The mutant allele inducing worker sterility is a. (A) There are three types of virgin queens: AA , Aa, and aa. Each queen mates n times. Of those matings, n − m are with wild-type males (type A) and m are with mutant males (type a). Hence, there are 3(n + 1) types of fertilized queens (colonies). (B) Relative proportions of offspring for each colony type if the mutant allele, a, for worker sterility is recessive. For example, if the queen’s genotype is Aa, then half of her sons are A and the other half are a. We denote this by A + a. If the queen’s genotype is aa and she has mated with both types of males, 0< m < n, then she has both Aa and aa workers (in proportion n − m and m, respectively); her Aa workers produce male eggs, which have an equal proportion of A and a genotypes. (C) Relative proportions of offspring for each colony type if the mutant allele, a, for worker sterility is dominant.
Figure 2
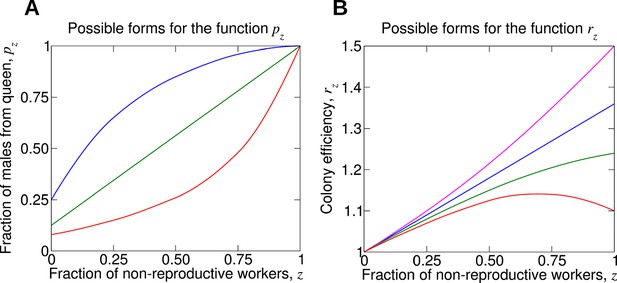
For understanding the evolution of non-reproductive workers, the following two functions are crucial.
(A) The function pz denotes the fraction of male offspring that come from the queen if a fraction, z, of the workers are non-reproductive. Therefore, 1 − pz is the fraction of male offspring that come from the workers. Clearly, pz should be an increasing function. More workers that are sterile means a larger fraction of males that come from the queen. If all workers are non-reproductive, then all males come from the queen, p1 = 1. (B) The function rz denotes the reproductive rate (or efficiency) of the colony if a fraction, z, of the workers are non-reproductive. Without loss of generality, we normalize such that r0 = 1. If worker sterility has an advantage, then it should increase colony efficiency for some values of z, but the function rz need not be monotonically increasing. It is possible that maximum colony efficiency is obtained for an intermediate value of z. Several possibilities for the colony efficiency function, rz, are shown.
Figure 3
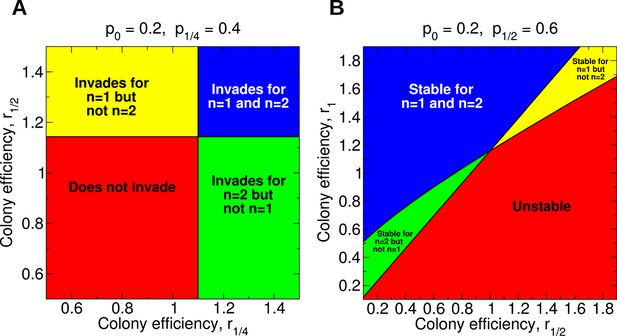
Regions of the parameter space for the evolution of non-reproductive workers for single and for double mating.
(A) For single mating, n = 1, the invasion of a recessive worker sterility allele depends on the parameters p0 and r1/2; for double mating, n = 2, it depends on the parameters p0, p1/4, and r1/4. (B) The evolutionary stability of a recessive worker sterility allele depends on the parameters p0, r1/2, and r1 for single mating, and on the parameters p1/2, r1/2, and r1 for double mating. We set r0 = 1 as baseline.
Figure 4
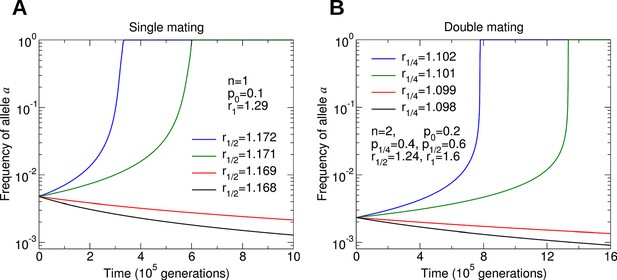
Numerical simulations of the evolutionary dynamics nicely illustrate the conditions specified by Equations 1 and 2.
The sterility allele is recessive. For numerically probing invasion, we use the initial condition and . We set r0 = 1. A: Single mating, n = 1. Parameters p0 = 0.1 and r1 = 1.29. B: Double mating, n = 2. Parameters p0 = 0.2, p1/4 = 0.4, p1/2 = 0.6, r1/2 = 1.24 and r1 = 1.6.
Figure 5
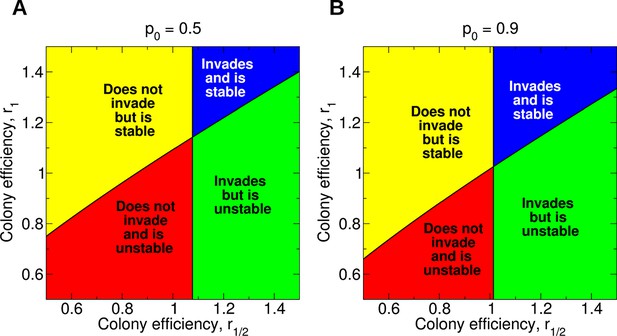
Evolution of non-reproductive workers for single mating (n = 1).
We consider a recessive sterility allele, a. There are four possible scenarios: The mutant allele cannot invade but is evolutionarily stable (bistability); the mutant allele can invade and is evolutionarily stable; the mutant allele can invade but is unstable (coexistence); the mutant allele cannot invade and is unstable. Only three parameters matter: p0, r1/2, and r1; p0 denotes the fraction of male offspring that come from the queen if there are no sterile workers in the colony (z = 0); r1/2 and r1 denote respectively the reproductive rate (efficiency) of the colony if z = 1/2 and z = 1 of all workers are sterile. The baseline value is r0 = 1. (A) Phase diagram for p0 = 0.5. (B) Phase diagram for p0 = 0.9. As p0 gets closer to 1, the intersection of the critical curves approaches the point (r1/2,r1) = (1,1).
Figure 6
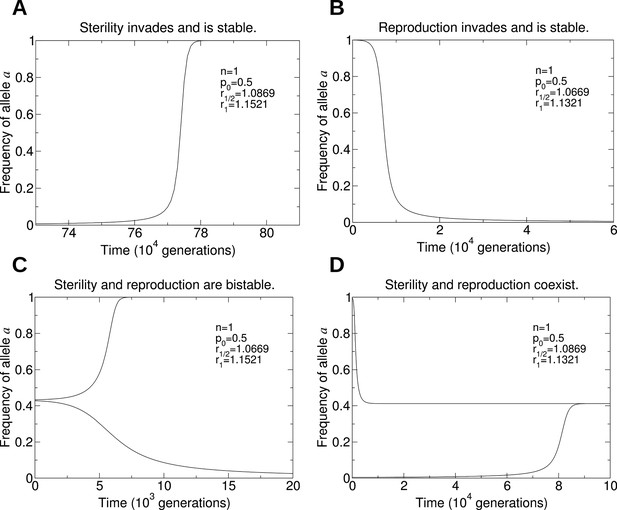
Numerical simulations of the evolutionary dynamics that show the four behaviors in Figure 5A.
The sterility allele is recessive, and we consider single mating (n = 1). For each of the four panels, we use the initial conditions: A: and ; B: and ; C: and (lower curve), and and (upper curve); D: and (lower curve), and and (upper curve). We set r0 = 1. A: Parameters p0 = 0.5, r1/2 = 1.0869, and r1 = 1.1521. B: Parameters p0 = 0.5, r1/2 = 1.0669, and r1 = 1.1321. C: Parameters p0 = 0.5, r1/2 = 1.0669, and r1 = 1.1521. D: Parameters p0 = 0.5, r1/2 = 1.0869, and r1 = 1.1321.
Figure 7
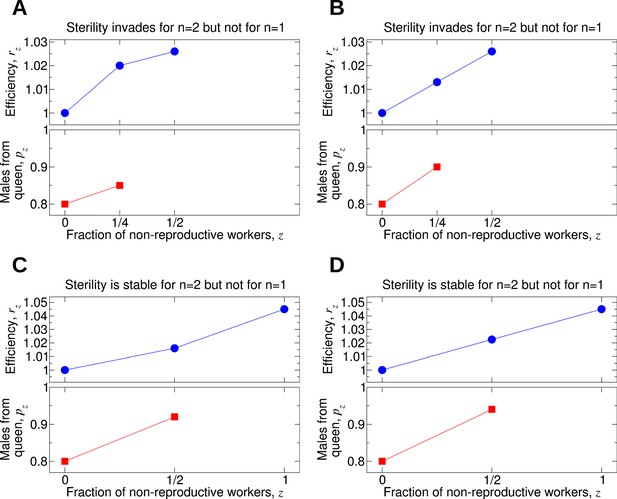
Comparing the effect of single mating (n = 1) and double mating (n = 2) on the evolution of worker sterility.
Whether or not single or double mating favors the evolution of worker sterility depends on the functions pz and rz. The function pz specifies the fraction of male offspring that come from the queen if a fraction, z, of all workers in the colony is non-reproductive. The function rz specifies the reproductive rate (or efficiency) of the colony if a fraction, z, of all workers in the colony is non-reproductive. We consider a recessive mutant allele, a, for worker sterility. (A, B) For these parameter choices, the mutant allele causing worker sterility can invade for double mating but not for single mating. (C, D) For these parameter choices, the mutant allele causing worker sterility is evolutionarily stable for double mating but not for single mating.
Figure 8
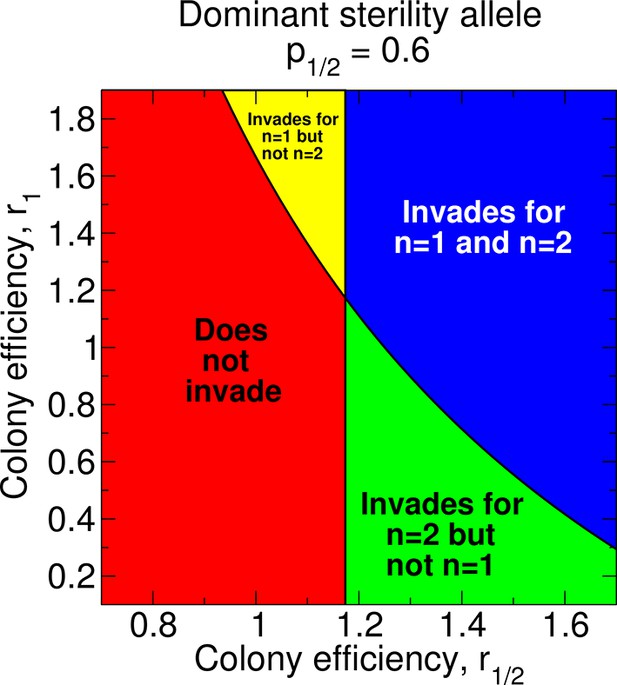
Regions of the parameter space and evolution of worker sterility for a dominant sterility allele.
The evolutionary invasion of a dominant worker sterility allele depends on values of the parameters p1/2, r1/2, and r1 for single mating, n = 1, and on values of the parameters p1/2 and r1/2 for double mating, n = 2. The figure shows four parameter regions indicating whether or not worker sterility can evolve for single or double mating. We set r0 = 1 as baseline.
Figure 9
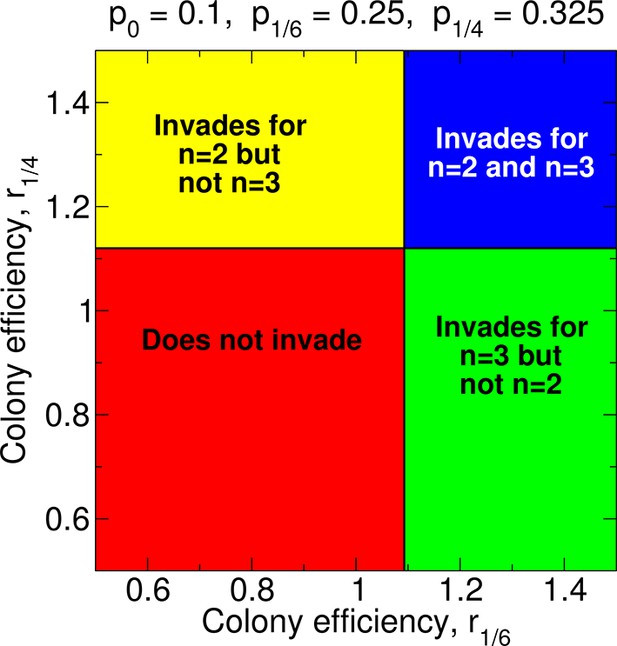
Regions of the parameter space and evolution of worker sterility for double and for triple mating.
For double mating, n = 2, the invasion of a recessive worker sterility allele depends on the parameters p0, p1/4, and r1/4; for triple mating, n = 3, it depends on the parameters p0, p1/6, and r1/6. We set r0 = 1 as baseline.
Figure 10
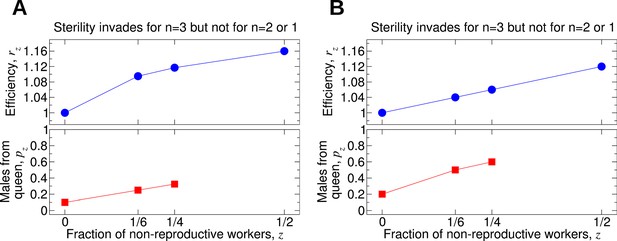
Comparing the effects of single mating (n = 1), double mating (n = 2), and triple mating (n = 3) on the evolution of worker sterility.
Whether or not triple mating favors the evolution of worker sterility depends on the functions pz and rz. We consider a recessive mutant allele, a, for worker sterility. (A, B) For these parameter choices, the mutant allele causing worker sterility can invade for triple mating but not for double or single mating.
Tables
Table 1
Numerical experiments. We randomly select the two relevant colony efficiency values from a bivariate normal distribution. For Procedure 1, the two efficiency values are uncorrelated. For Procedure 2, they are correlated (with correlation 0.8). The results of the numerical experiment for Figures 3A and 8 are shown. For Figure 3A, which describes a recessive allele inducing non-reproductive workers, we randomly generate values for r1/4 and r1/2. For Figure 8, which describes a dominant allele inducing non-reproductive workers, we randomly generate values for r1/2 and r1. The table shows the likelihood of the four possible outcomes: non-reproductive workers (i) do not invade, (ii) invade for single mating but not for double mating, (iii) invade for double mating but not for single mating, and (iv) invade for both single and double mating. For this particular randomization experiment, double mating is more favorable than single mating for the invasion of non-reproductive workers. All p values are exactly as in the corresponding Figures.
| Does not | Invades for n = 1 | Invades for n = 2 | Invades for both | |
|---|---|---|---|---|
| invade | but not n = 2 | but not n = 1 | n = 1 and n = 2 | |
| Figure 3A, Proc. 1, recessive | 0.7769 | 0.0644 | 0.1465 | 0.0122 |
| Figure 3A, Proc. 2, recessive | 0.8237 | 0.0177 | 0.0997 | 0.0589 |
| Figure 8, Proc. 1, dominant | 0.7944 | 0.0129 | 0.0830 | 0.1097 |
| Figure 8, Proc. 2, dominant | 0.7927 | 0.0146 | 0.0260 | 0.1667 |
Table 2
Numerical experiments. With the equivalent Procedures, we explore the likelihood of the four scenarios regarding invasion and/or stability for single mating. Results of the numerical experiment for Figure 5A, describing a recessive allele, are shown. We randomly generate values for r1/2 and r1. The value p0 = 0.5 is exactly as in Figure 5A.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The evolution of non-reproductive workers in insect colonies with haplodiploid genetics
eLife 4:e08918.
https://doi.org/10.7554/eLife.08918
