Traveling waves across scales: Different mechanisms but same canonical computation?
- Université Paris Cité, CNRS, Integrative Neuroscience and Cognition Center, France
- Institut Universitaire de France (IUF), France
- Aix-Marseille Université, CNRS, Institut de Neurosciences de la Timone, UMR7289, France
Figures
Figure 1
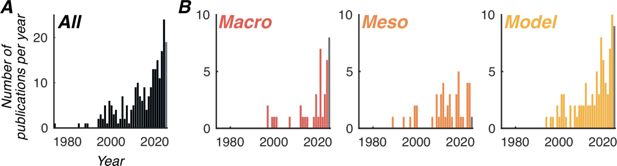
Publication trend on traveling waves (from 1970 to August 2025).
(A) PubMed search for (travel(l)ing wave(s) OR front propagation OR cortical propagation OR horizontal propagation) AND (cortex) NOT (myosin OR actin). The search was constrained to Title/Abstract. (B) Same search constrained to NOT (review). Additional PubMed search terms were added to what we called Macro, Meso, and Model categories (red, dark orange, light orange distributions, respectively). Macro: AND (‘EEG’ OR ‘MEG’ OR ‘electroencephalography’ OR ‘magnetoencephalography’ OR ‘ECoG’ OR ‘electrocorticography’ OR ‘intracranial’). Meso: AND (‘intracellular recordings’ OR ‘single-unit activity’ OR ‘SUA’ OR ‘multi-unit activity’ OR ‘MUA’ OR ‘local-field potential’ OR ‘LFP’ OR ‘two-photon microscopy’ OR ‘multi-electrode array’ OR ‘MEA’ OR ‘voltage-sensitive dye imaging’ OR ‘VSDI’ OR ‘optical imaging’). Model: AND (‘model’ OR ‘computational’). The gray bar in each plot represents the publications in 2025 (from January to August).
Figure 2
Framework based on region-dependent integration time constants and conduction delays.
The visual system is used as a test case. (A) General principle. (A1) To simulate how a transient activity is transmitted by one emitter and integrated by a downstream recipient structure, we applied 3 transformations: NL, non-linearity due to spike threshold (see Chen et al., 2012; Girard et al., 2001); d, axonal delay (see Girard et al., 2001); and τ, a convolution with a decreasing exponential function of time constant. NL, d, and τ were all estimated from literature (see Table 1). (A2) Activity with no transformation (leftmost), and predicted response to the propagation and integration of the V1 transient successively adding up the three parameters (power-law exponent 4 for NL, a delay of 2 ms, and a time constant of 24 ms; inspired from V1-V2 communication). Vertical blue ticks on curves indicate the latency of the V2 transient response. Open circles show half-height time approximating the phase of the transient response. (A3) Phases from A2 plotted as a function of delay. (B) First-order TW. B1. Intra-area (here V1) propagation along four equally distant positions. (B2) V1 response to a transient propagating along the four positions. Vertical blue ticks on curves indicate the latency of the transient response. Open circles show the phase. (B3) Phases as a function of delay. (C) Second-order TW. (C1) Dynamic transformation of a transient along the hierarchical feedforward and feedback interactions between V1-V2-V3-V4 (same color code in B2-B3). (C2) Four different steps of transformation of the V1 output transient along V1-V4. From left to right, a single feedforward signal, one feedforward-feedback loop (from V2 to V1, V3 to V2 etc…), two, and three loops. (C3) Phases from B2 as a function of delay. Each of the four steps in B2 is connected with lines of increasing widths.
Tables
Table 1
Communication (blue) and integration (green) neuronal space and time constants (within visual cortex).
Speeds for communication after V2 were inferred from axonal diameter of connections between V1-V4 (Innocenti et al., 2014; Rockland et al., 1994), V1-MT (Nhan, 2010; Rockland, 1989), V2-MT (Rockland, 1995) and V1-V2 (Rockland and Virga, 1990), using a documented conversion formula (Innocenti et al., 2014). For V4-FEF, the speed was estimated using measured propagation delay and distance reported in corresponding columns. Time constants for V2 were estimated from simulations (Chaudhuri et al., 2015) All other values are extracted from listed references.
| Distance (mm) | Propagation Delay (ms) | Speed (m/s) | Time Constant (ms) | Latency (ms) (Lamme and Roelfsema, 2000) (earliest-mean) | ||
|---|---|---|---|---|---|---|
| V1-V1 | 6 (Angelucci et al., 2002) | 6–60 (Girard et al., 2001; Muller et al., 2014; Nowak and Bullier, 1997; Reynaud et al., 2012; Grinvald et al., 1994) | 0.1–0.5 (Muller et al., 2014; Girard et al., 2001; Nowak and Bullier, 1997; Grinvald et al., 1994; Reynaud et al., 2012) | V1 | 25–34 (Chemla et al., 2019) | 35–72 |
| V1-V2 | 9.3 Markov et al., 2013) | 1 (V1-V2) 1.5 (V2-V1) (Girard et al., 2001) | 1–7 (Girard et al., 2001) | V2 | 34–38 (Chaudhuri et al., 2015) | 54–73 |
| V1-V4 | 14.8 (Markov et al., 2013) | 3 (V1-V4) 9 (V4-V1) (van Kerkoerle et al., 2014) | 2–6 | V4 | 35–40 (Zeraati et al., 2023) | 61–106 |
| V1-MT | 12.5 (Markov et al., 2013) | 1.2–1.4 (Movshon and Newsome, 1996) | 8–11 | MT | 64–77 (Murray et al., 2014) | 39–76 |
| V4-FEF | 40 (Markov et al., 2013) | 6.5 (Noudoost et al., 2021) | ~6 | FEF | 127–195 (Murray et al., 2014) | 43–91 |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Traveling waves across scales: Different mechanisms but same canonical computation?
eLife 14:e106753.
https://doi.org/10.7554/eLife.106753
