Inference of gene regulation functions from dynamic transcriptome data
- Technische Universität München, Germany
- Max-Planck Institute for Biophysical Chemistry, Germany
Figures
Figure 1
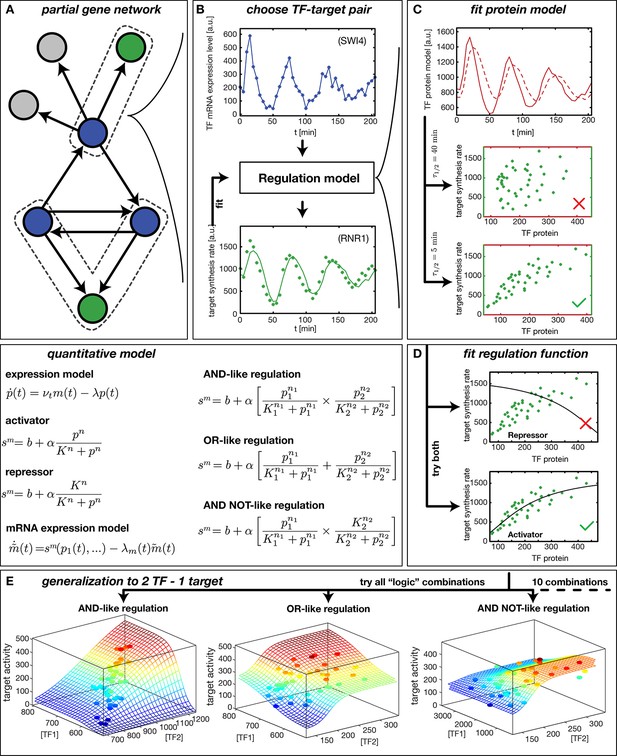
Reconstruction of regulation functions.
(A) We select a target gene (green) and TFs (blue), which are known from the literature to interact with the target gene. We consider only target genes and corresponding TFs, which show significant variation in our dataset. (B) The fitting task is to find a regulation model using the TF mRNA expression level (upper plot), so that the time series of the target synthesis rate (dots in lower plot) is best described by the model synthesis rate (solid curve in lower plot). (C) We describe the concentration of active TF protein by a simple model with translation rate and linear degradation rate (see box quantitative model). For a correctly chosen the target gene synthesis rate plotted against the TF protein concentration collapses to a curve (bottom plot). (D) Together with a regulation function (target synthesis rate as a function of TF protein ) is estimated. For a single TF the regulation function has four parameters () and two possible directions of regulation: activator and repressor (see box mathematical model). To find the right regulatory direction we fit both and select the one, which yields the better score. (E) Two TFs can interact in multiple ways to generate a two dimensional combinatorial regulation function (Buchler et al., 2003). For two TFs we estimate the protein models and six parameters for the regulation function. There are 10 non-trivial regulatory analog 'logic' operations to test, of which 3 examples are depicted (see box quantitative model for the corresponding equations).
Figure 2 with 1 supplement
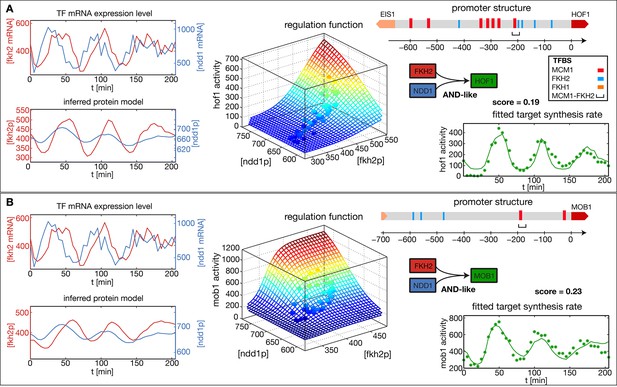
Reconstructed regulation functions of two genes in the CLB2 cluster.
For both target genes the measured TF expression level, the inferred protein level, the estimated regulation function with corresponding measured data points and the fit to the target synthesis rate are shown. Additionally predicted binding sites for relevant TFs within the target gene promoter regions are depicted. Both target genes, Hof1 and Mob1, are regulated by Fkh2 and Ndd1 (which is recruited to the complex Mcm1-Fkh2).
Figure 2—figure supplement 1
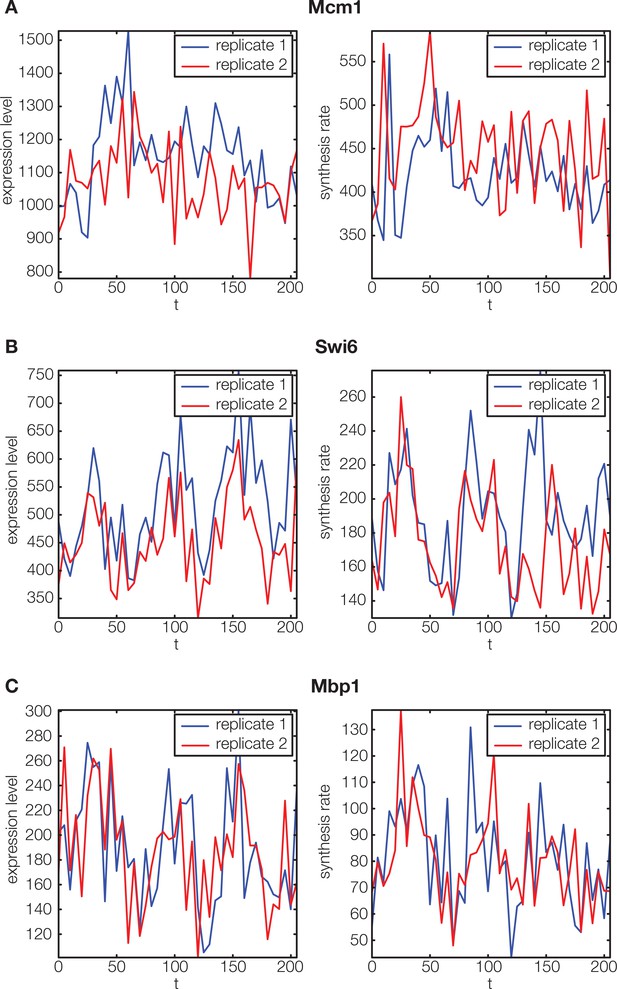
Non-periodic cell cycle regulators.
https://doi.org/10.7554/eLife.12188.005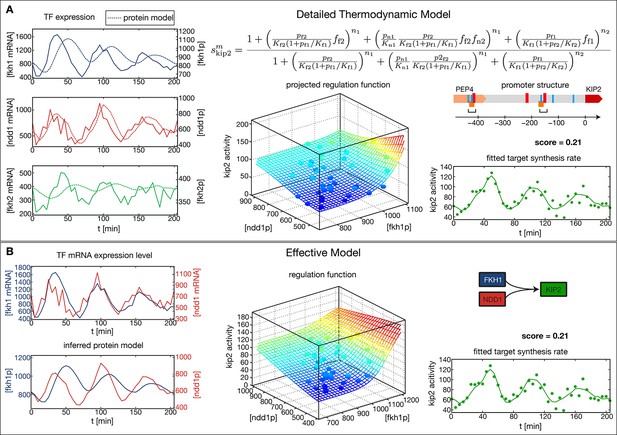
Figure 3 with 2 supplements
Comparison of the effective regulation function to a detailed promoter model.
Target gene Kip2 within the CLB2 cluster is predominantly regulated by three input factors Fkh1, Fkh2 and Ndd1. (A) Results of fitting a detailed promoter model, using all three input factors. The regulation model is derived from the promoter structure which contains overlapping binding sites for Mcm1-Fkh2 and Fkh1, using a thermodynamic approach as detailed in Bintu et al. (2005). The displayed projected regulation function has been plotted with Fkh2 fixed at its average value which leads to only minor deviations from the full model. (B) Results for fitting an effective model to Kip2. All three combinations of two out of three input factors have been tested with Fkh1/Ndd1 yielding the best score.
Figure 3—figure supplement 1
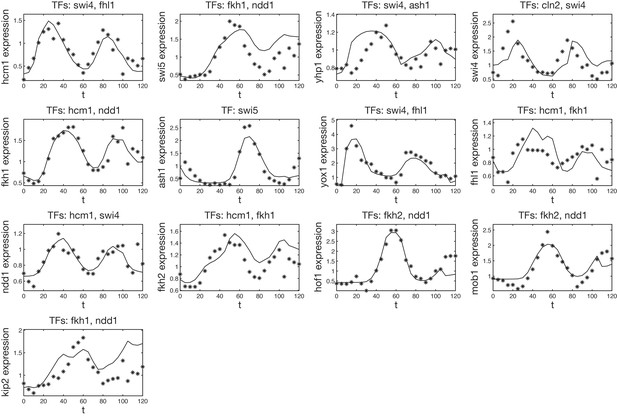
Validation of our inferred GRFs with an independent dataset.
All inferred GRFs presented in this article have been tested on the microarray dataset previously published in Pramila et al. (2006). To match the scale of the data the GRFs have been inferred from, all TF data have been linearly transformed such that their minimum and maximum match those of the corresponding data in our dataset (see ‘Materials and methods’ for details). Shown are the reversely transformed model output (solid line) with the target gene expression level of the test dataset (stars). A comparison of the points in protein space which are used for the output in our dataset and the test dataset is shown in Figure 3—figure supplement 2.
Figure 3—figure supplement 2
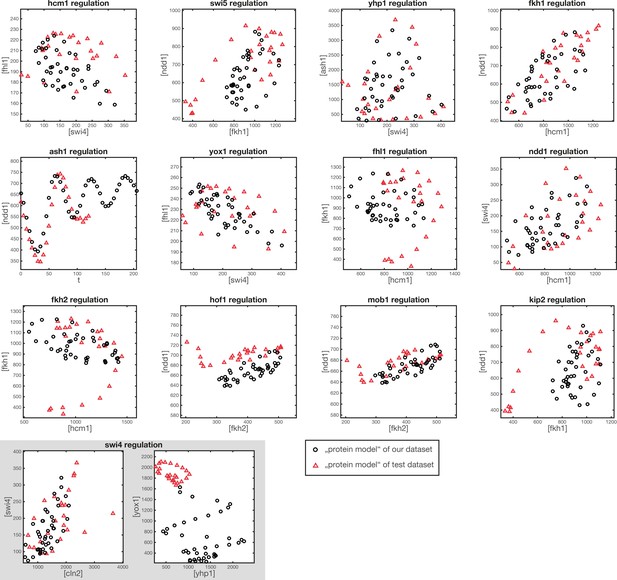
Comparison of protein space coverage.
Shown are the values of (inferred) protein concentration, which are used to generate the GRF outputs from our dataset (black circles) and from the test dataset (red triangles). The points in protein space generated from the test dataset are used for the model output shown in Figure 3—figure supplement 1.
Figure 4 with 8 supplements
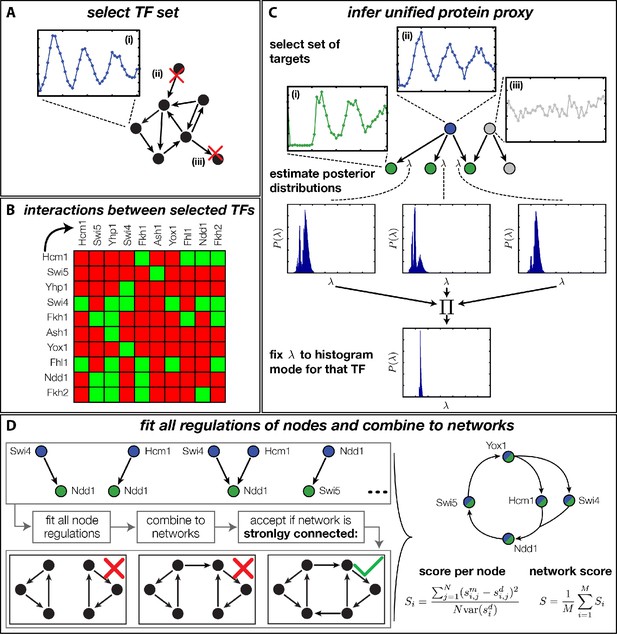
Finding a regulatory model for the transcriptional cell cycle oscillator.
(A) A set of potentially constituent TFs is selected. We require that these genes are (i) periodically expressed, (ii) regulate at least one other gene within the set and (iii) are regulated by at least one other gene within the set. (B) Interaction table of the resulting set of genes (listed on the axis), as annotated in the literature. A green square indicates that the corresponding gene of that row regulates the respective gene on the column. (C) Before fitting regulation functions to target genes we pre-determine the effective protein degradation rate for each TF. To that end we first select a set of target genes, which are (i) periodically expressed, (ii) are well fitted by the TF and (iii) if there are other TFs regulating the target gene, they must be non-periodic so that they cannot contribute in explaining the expression pattern of the target gene. We then use MCMC to sample from the posterior distribution of the fitting parameters of each target gene and create histograms for the marginal distributions over the protein parameter. The consensus is fixed to the highest peak of the product histogram. (D) To each gene in the set of potentially constituent gene regulation models are fitted for all single inputs and all combinations of two inputs. To each fit we calculate a normalized score as the averaged squared residuals of the fit, divided by the data variance of the target synthesis rate. These 'regulatory nodes' are combined to networks, which we require to be strongly connected (as illustrated on the bottom). The resulting set of possible network models are scored by the average normalized fitting score of the nodes and ranked.
-
Figure 4—source data 1
Table of interactions between cell cycle TFs with references.
If evidence exists that the gene heading a row transcriptionally regulates the gene heading a column, the corresponding references are listed in the respective field. A '0' indicates that no direct evidence for a transcriptional regulation exists.
- https://doi.org/10.7554/eLife.12188.010
-
Figure 4—source data 2
Data for protein model inference.
This table contains the inferred protein model parameter for each TF in the cell cycle oscillator model and both replicated. Additionally listed are the sets of target genes on which the inferences were performed.
- https://doi.org/10.7554/eLife.12188.011
-
Figure 4—source data 3
List of inferred regulation directions of genes in the trancriptional cell cycle oscillator
Direction of regulation (activating or repressing) and, if available, references for each best fitted regulation function in the transcriptional cell cycle oscillator model.
- https://doi.org/10.7554/eLife.12188.012
Figure 4—figure supplement 1
Fitted GRF for Hcm1.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity.
Figure 4—figure supplement 2
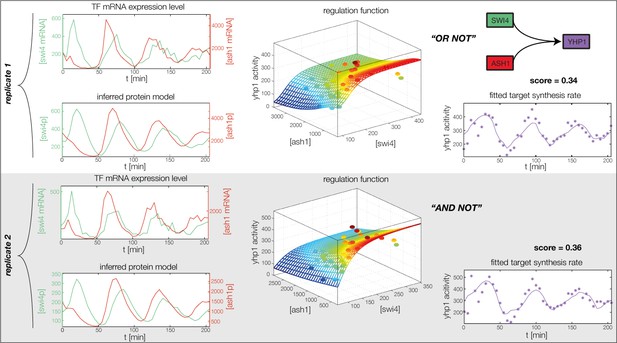
Fitted GRF for Yhp1.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity.
Figure 4—figure supplement 3
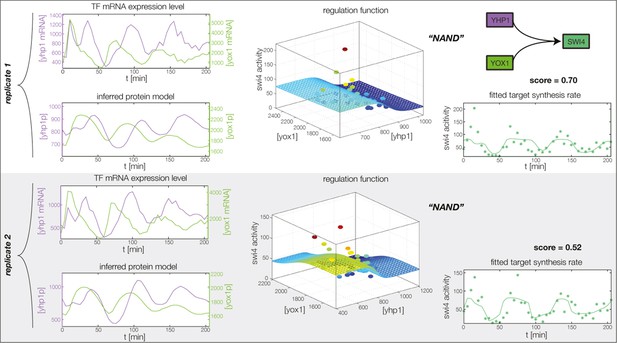
Fitted GRF for Swi4.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity. This GRF will be revised below.
Figure 4—figure supplement 4
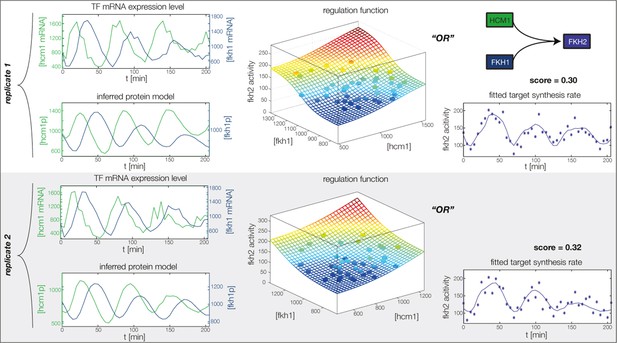
Fitted GRF for Fkh2.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity.
Figure 4—figure supplement 5
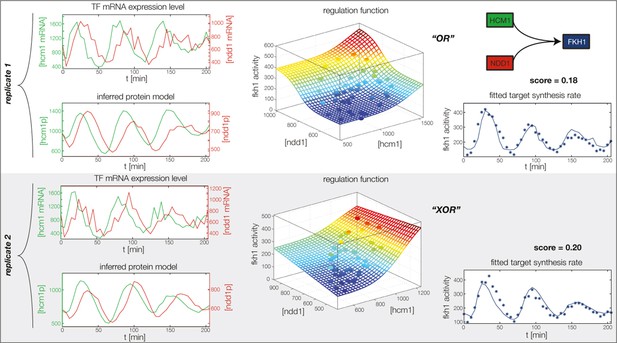
Fitted GRF for Fkh1.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity.
Figure 4—figure supplement 6
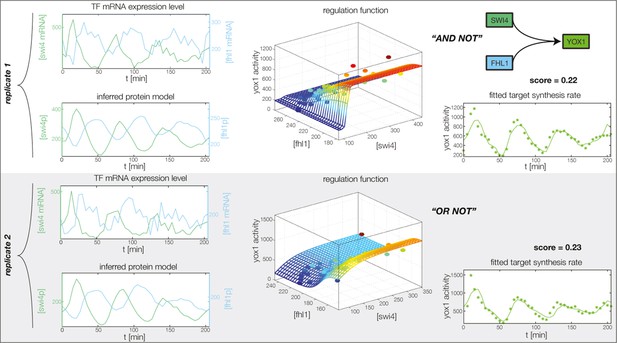
Fitted GRF for Yox1.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity.
Figure 4—figure supplement 7
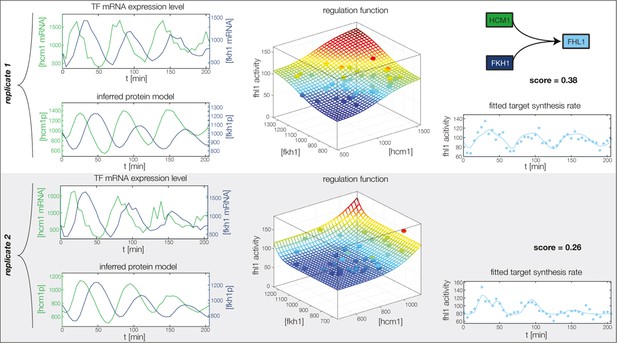
Fitted GRF for Fhl1.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity.
Figure 4—figure supplement 8
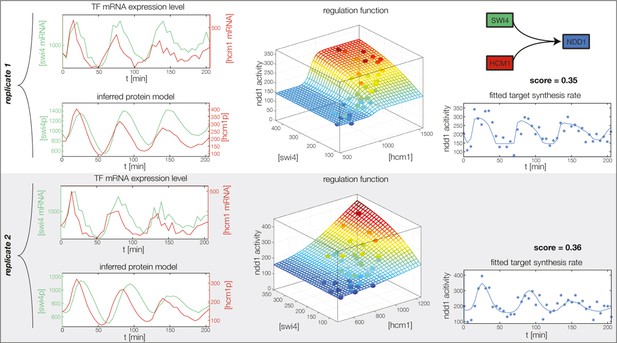
Fitted GRF for Ndd1.
Depicted for both replicates are transcript levels of the TFs, the inferred protein levels, the inferred GRF and a comparison of model output and data for the target gene activity.
Figure 5 with 6 supplements
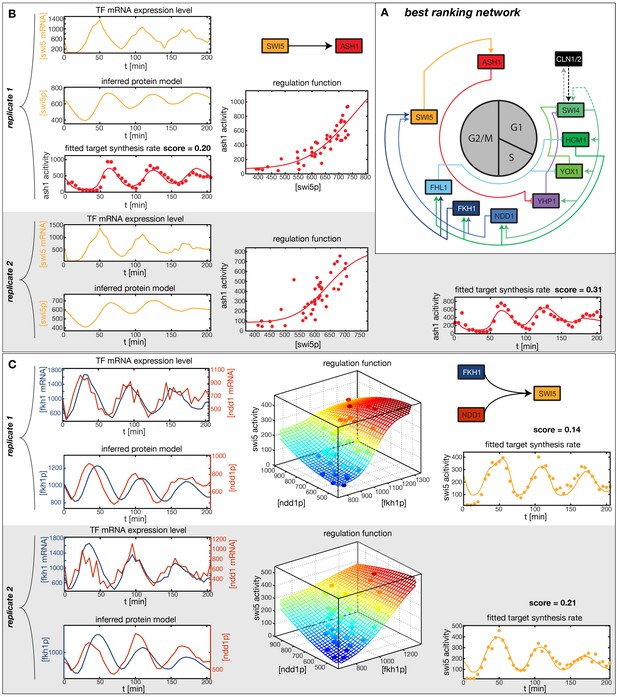
Results of node fitting in the cell cycle network.
(A) Regulation diagram of our best ranking model for a transcriptional cell cycle oscillator. Arrows represent positive (pointing clockwise) and negative (pointing counter-clockwise) interactions and are color-coded with respect to their corresponding TF. Only the regulatory interactions indicated by solid lines resulted from our network inference method, while the additional interactions indicated by dashed lines were introduced in the subsequent manual analysis (see main text). (B) Example of a regulation model with two input factors: Swi5 is regulated by Fkh1 and Ndd1 by an analog XOR-like function. (C) Example of a one input factor regulation model: Ash1 is activated by Swi5. Depicted in (B) and (C) are, for both replicates respectively, data of the TF(s) total mRNA expression level, the inferred TF protein time series, the fitted regulation function and the resulting target synthesis rate. Data points of the target synthesis rate are displayed as stars or colored spheres.
Figure 5—figure supplement 1
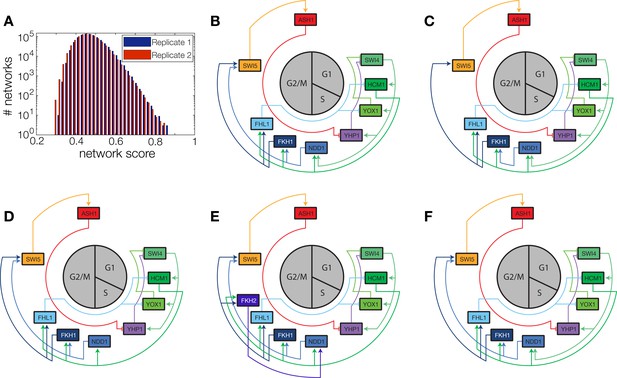
Network scores and best ranking networks.
(A) Histograms of network scores in replicate datasets 1 and 2, respectively. (B–F) The five best ranking networks (rank 1–5). (B) best ranking network. (C) Rank 2. In comparison to (B) Swi5 is regulated only by Fkh1. (C) Rank 3. In comparison to (B) Ndd1 is regulated only by Hcm1. (E) Rank 4. In comparison to (B) Fkh2 is part of the network, regulating Ndd1 together with Hcm1. (F) Rank 5. In comparison to (B) Yox1 is regulated only by Fhl1.
Figure 5—figure supplement 2
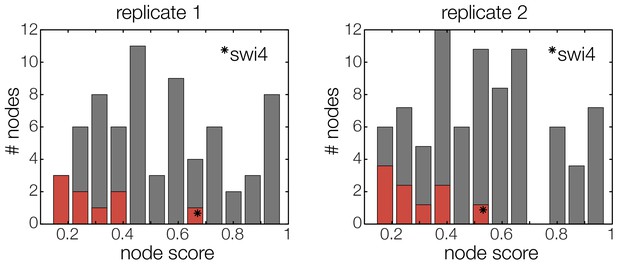
The GRF for Swi4 is an outlier.
Histograms for the scores of all possible GRFs for each TF selected for the cell cycle oscillator. Marked in red are the scores of the respective best ranking GRF for each TF. The outlier in both replicates (marked with star) represents the GRF of Swi4, scoring considerably worse than the other best ranking GRFs.
Figure 5—figure supplement 3
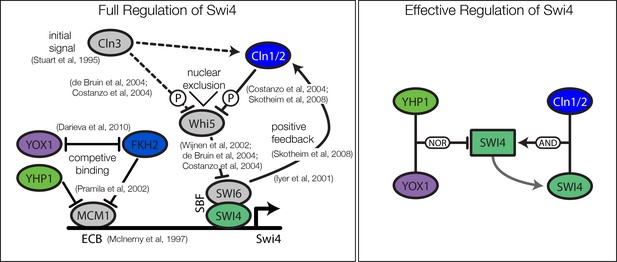
Current biological model and the effective model for regulation of Swi4.
Also depicted are references with experimental evidence for the corresponding interaction.
Figure 5—figure supplement 4
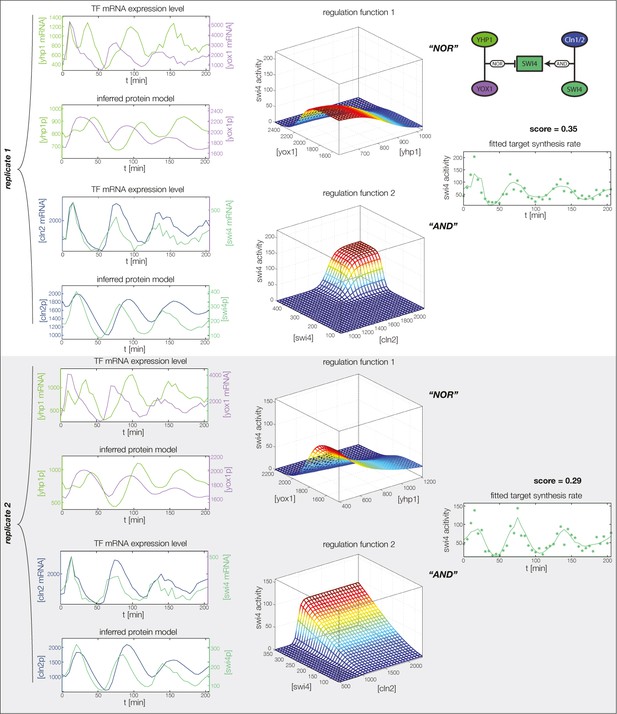
GRF for Swi4 with cyclin input.
Aside from repressors Yhp1 and Yox1, Swi4 is also auto-activated by SBF (Swi4-Swi6), which in turn is (indirectly) activated by Cln1 and Cln2. We model this regulation by additional input from Swi4 and Cln2.
Figure 5—figure supplement 5
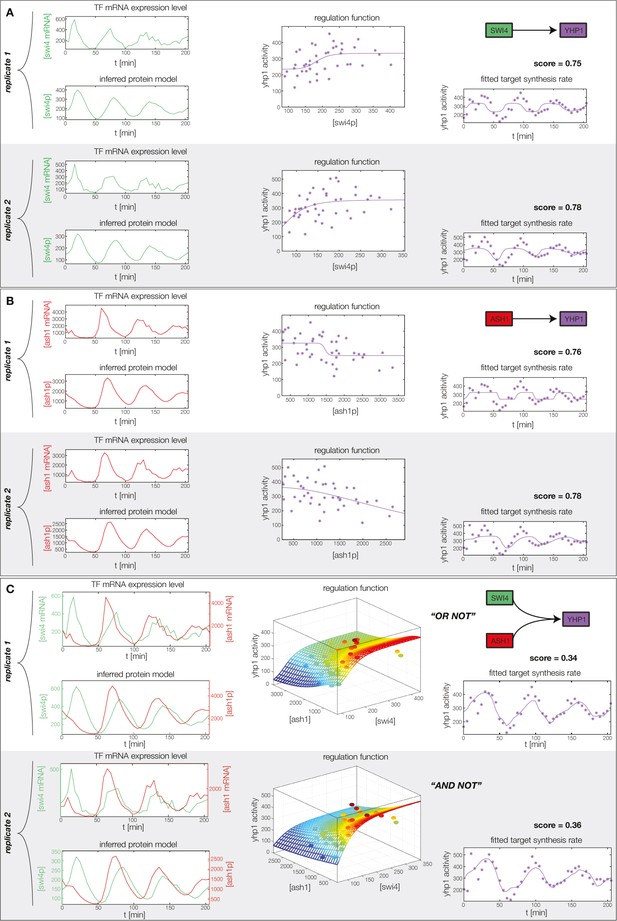
Concerted regulation by both Swi4 and Ash1 are necessary to model the expression pattern of Yhp1.
(A) shows a fit of the GRF for Yhp1 with Swi4 as only input factor, while (B) shows a fit with Ash1 as only input factor. Both explain less than 25% of the data variance in both replicates. (C) Combined regulation of Yhp1 by Swi4 and Ash1 yields a satisfactory fit.
Figure 5—figure supplement 6
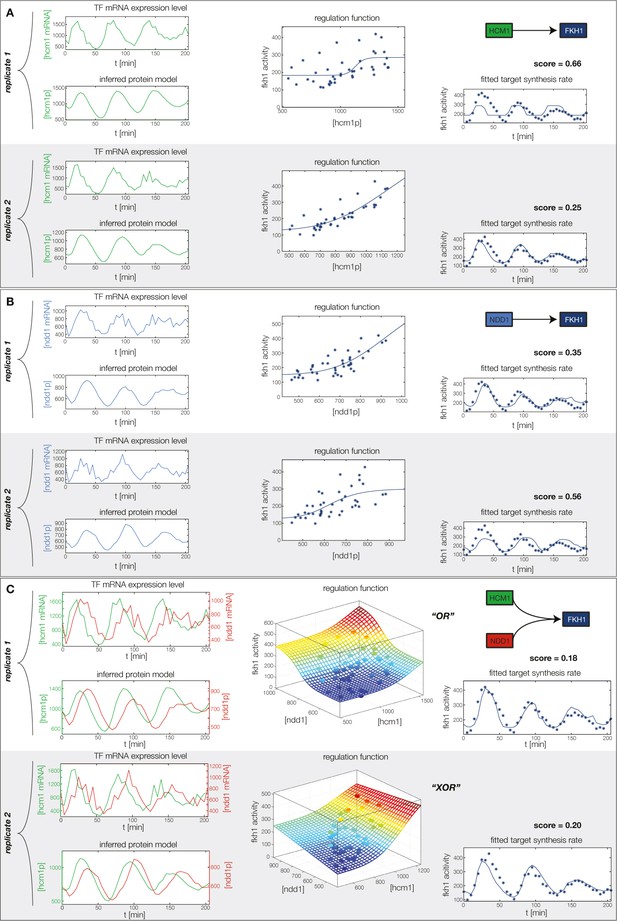
Concerted regulation by both Hcm1 and Ndd1 are necessary to model the expression pattern of Fkh1.
(A) shows a fit of the GRF for Fkh1 with Hcm1 as only input factor, while (B) shows a fit with Ndd1 as only input factor. (C) Combined regulation of Fkh1 by Hcm1 and Ndd1 yields superior fits to single inputs.
Figure 6 with 2 supplements
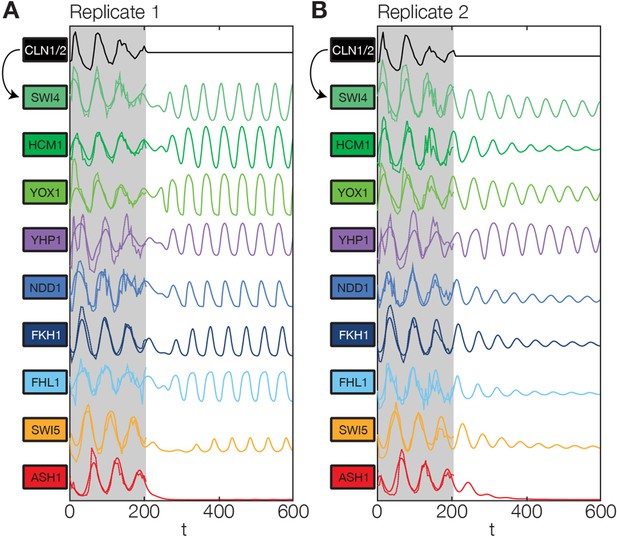
Simulation results of the reconstructed transcriptional cell cycle oscillator.
Simulated mRNA expression levels for all genes in the network are shown in arbitrary units and rescaled to equal sizes. For the first 205 min (shaded grey) Swi4 receives periodic input from Cln2 using measured expression data. After 205 min the input from Cln2 is set to a constant average value to simulate loss of cyclin activity. (A) The network inferred from replicate dataset 1 recovers sustained oscillations. (B) Oscillations in the network inferred from replicate dataset 2 dampen over time without periodic input.
Figure 6—figure supplement 1
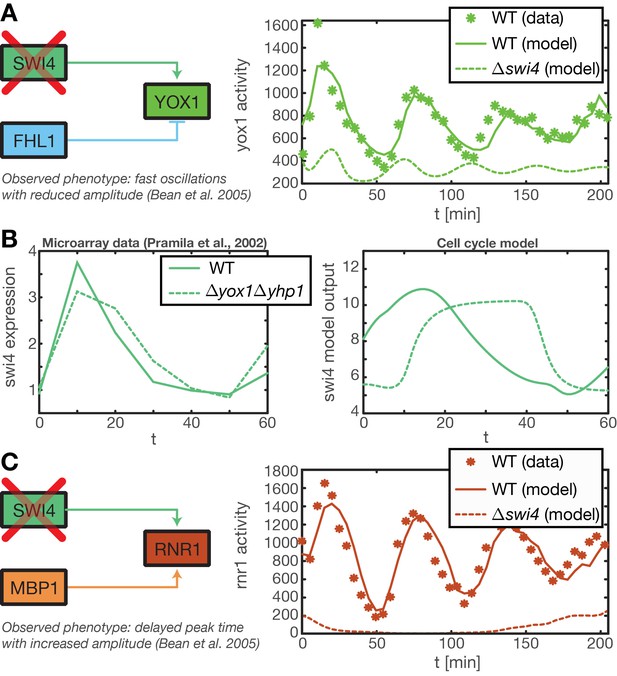
Test of predictions for mutant strains by model simulations.
(A) (Bean et al., 2005) reported that in a Swi4 deletion mutant the Swi4 target gene Yox1 shows heavily reduced expression and a weak oscillation with a period shorter than the cell cycle. This oscillation might results from secondary feedback loops in the transcriptional cell cycle network. We reproduced this behavior within our ODE model of the transcriptional cell cycle oscillator by setting Swi4 expression to zero. The resulting output for Yox1 shows the expected fast oscillations. (B) It has been shown that in a yhp1yox1 double mutant Swi4 expression exhibits a delayed and longer peak, reaching into S and G2 phase (Pramila et al., 2002). We could partially recapture this qualitative behavior with our ODE model of the transcriptional cell cycle oscillator by setting Yox1 and Yhp1 expression to zero. The resulting model output shows a prolonged peak duration, albeit a delayed onset that is not observed in the data. (C) In the same mutant strain as in (A) Rnr1, a target gene of Swi4 and Mbp1, was reported to have delayed peak time with an increases amplitude (Bean et al., 2005). This behavior cannot be reproduced within our model, because Mbp1 shows no periodic transcriptional activity in our data (see Figure 2—figure supplement 1).
Figure 6—figure supplement 2
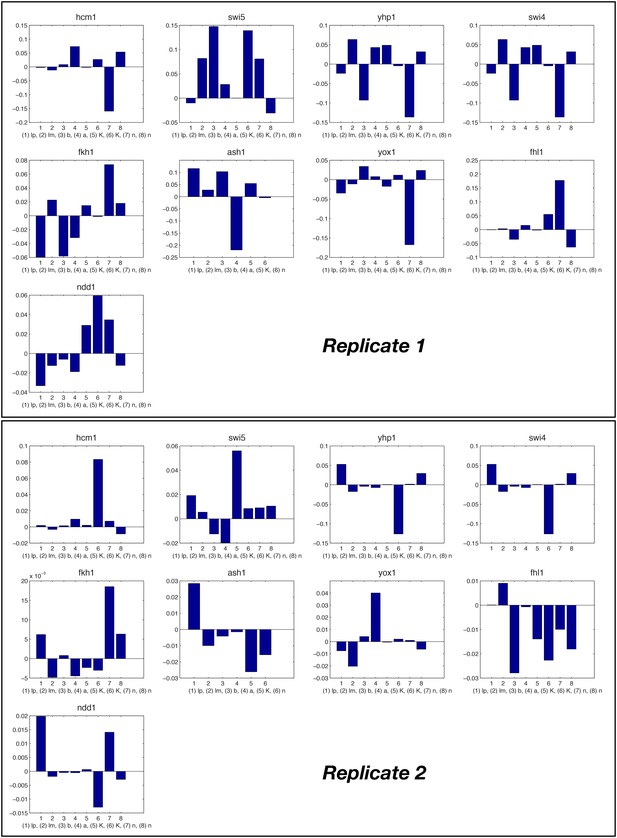
Relative change of model parameter after re-fitting the full ODE model compared to the individual fits.
To minimize propagation of errors at the individual nodes, the parameters of the GRFs optimized again for the network score of the ODE model, starting from their original value (see ‘Materials and methods’). The relative change of the majority of parameters is well below 10%.
Additional files
-
Source code 1
Software package for the inference of gene regulation functions
MATLAB (RRID:SCR_001622) implementations with complementing C function of all computational methods described in this work are provided in an accompanying source code archive.
- https://doi.org/10.7554/eLife.12188.031
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Inference of gene regulation functions from dynamic transcriptome data
eLife 5:e12188.
https://doi.org/10.7554/eLife.12188
