Rotating waves during human sleep spindles organize global patterns of activity that repeat precisely through the night
- Salk Institute for Biological Studies, United States
- Harvard Medical School, United States
- University of California, San Diego, United States
Figures
Figure 1 with 12 supplements
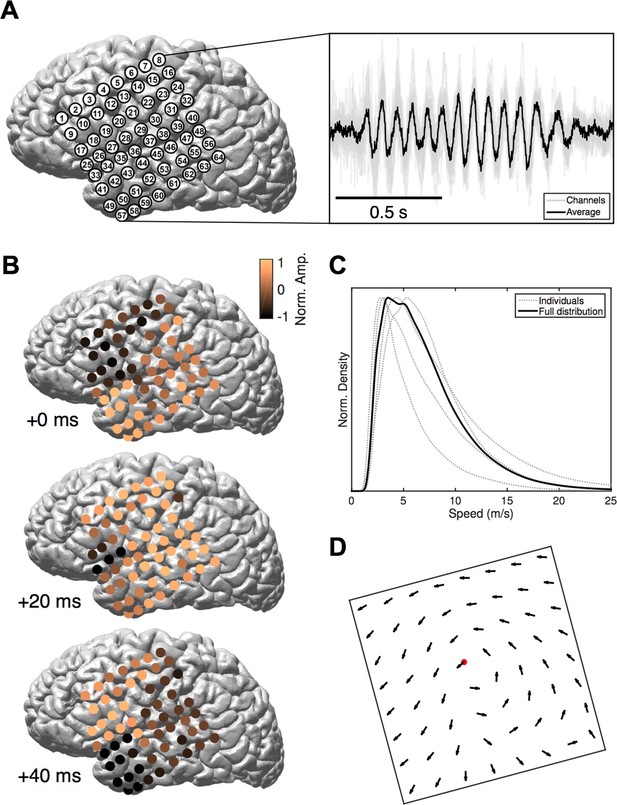
Rotating waves during spindles.
(A) Electrode placement for subject 1 (left), with a stereotypical spindling epoch observed on the array (right). The right panel depicts the average over channels (black) together with the individual channels (gray). (B) When visualized on the cortex, individual spindle cycles are often organized as rotating waves traveling from temporal (+0 ms, top) to parietal (+20 ms, middle) to frontal (+40 ms, bottom) lobes. (C) Phase speed distributions across subjects. Plotted is the kernel smoothing density estimate for individual subjects (gray dotted lines) and for the full distribution (black line). (D) The field of propagation directions, aligned on the putative rotation center and averaged across oscillation cycles and across subjects, shows a consistent flow in the temporal parietal frontal (TPF) direction. The center point is marked in red.
-
Figure 1—source data 1
Patient information and wave classification totals.
This CSV file provides patient age, sex, and the number of spindle oscillation cycles isolated in each class (total, expanding, rotating, and rotating TPF).
- https://doi.org/10.7554/eLife.17267.004
Figure 1—figure supplement 1
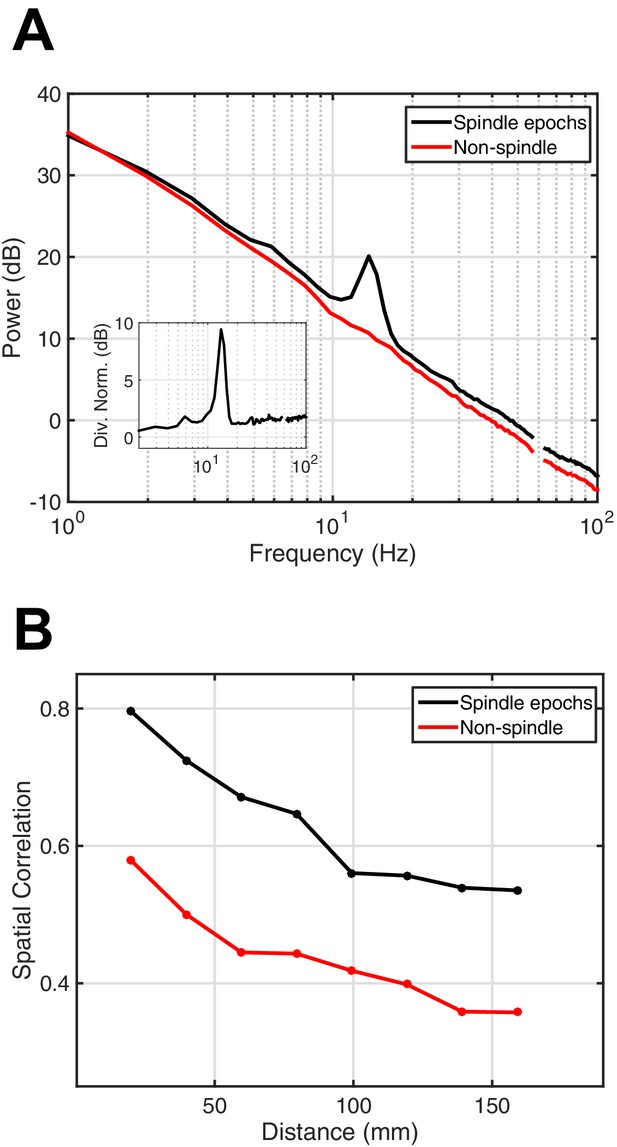
Power spectral density and spatial correlation analysis.
(A) Average power spectral density estimate for spindle epochs (black) and matched non-spindle epochs (red), illustrating the nearly 10 dB increase within the 11–15 Hz spindle band during algorithmically selected epochs (divisive normalization, inset). Power at line noise frequency omitted for clarity. (B) Average spatial correlation values for spindle (black) and non-spindle (red) epochs illustrate increased global correlations during spindles.
Figure 1—figure supplement 2
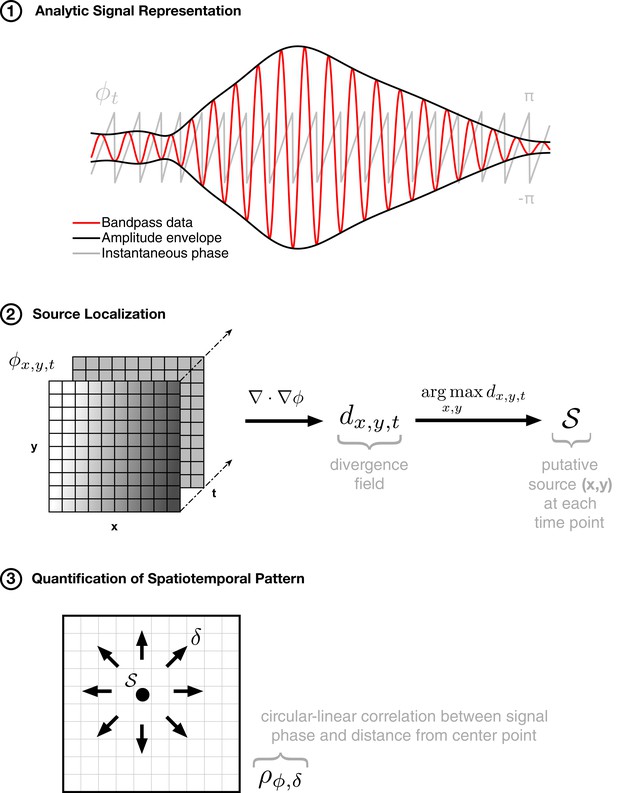
Method for isolating expanding spatiotemporal patterns.
The algorithmic approach to detecting expanding waves in noisy multichannel data proceeds in three steps: (1) phase extraction, through the analytic signal (Feldman, 2011) representation, followed by (2) center localization by taking the divergence of the phase gradient, and (3) quantification of the spatiotemporal pattern by calculating the circular-linear correlation of phase with distance from the center point. By finding an anchor point (in step 2) and then quantifying the spatial pattern of activity through the appropriate correlation metric (in step 3), we can capture the spatiotemporal pattern of expanding activity on the array in a single number ().
Figure 1—figure supplement 3
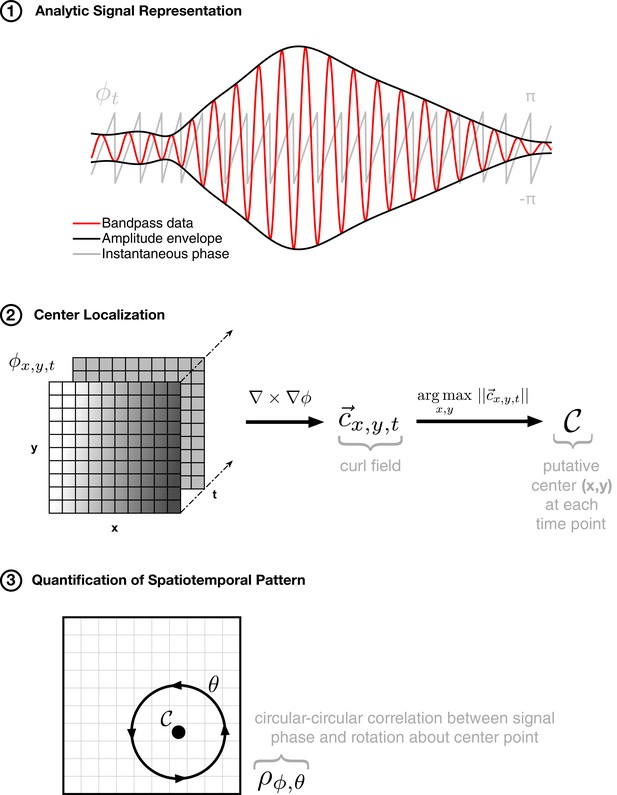
Method for isolating rotating spatiotemporal patterns.
The approach to detecting rotating waves in noisy multichannel data proceeds similarly to that for expanding waves: (1) phase extraction, followed by (2) center localization by taking the curl of the phase gradient, and (3) quantification of the spatiotemporal pattern by calculating the circular-circular correlation of phase with rotation about the center point. By finding an anchor point (in step 2) and then quantifying the spatial pattern of activity through an appropriate correlation metric (in step 3), we can capture the spatiotemporal pattern of rotating activity on the array in a single number ().
Figure 1—figure supplement 4
Analysis of 1528 spindles in Subject 1.
(A) Cumulative distribution function for expanding (blue) and rotational (red) correlation coefficients. Dotted lines indicate the 99th percentile from a random shuffling permutation test. Rotational waves exceeding the determined threshold exhibit a marked preference for the temporal parietal frontal (TPF) direction (inset). (B) Phase speed distributions were similar for both expanding and rotational waves. Plotted is the kernel smoothing density estimate with the constraint of positive support.
Figure 1—figure supplement 5
Vector field averaging controls.
(A) Average re-centered phase gradient directions over identified rotational cycles traveling in the TPF direction, illustrating the robustness of the multichannel detection algorithm. Center point marked in red. (B) Average re-centered phase gradient directions over expanding waves.
Figure 1—figure supplement 6
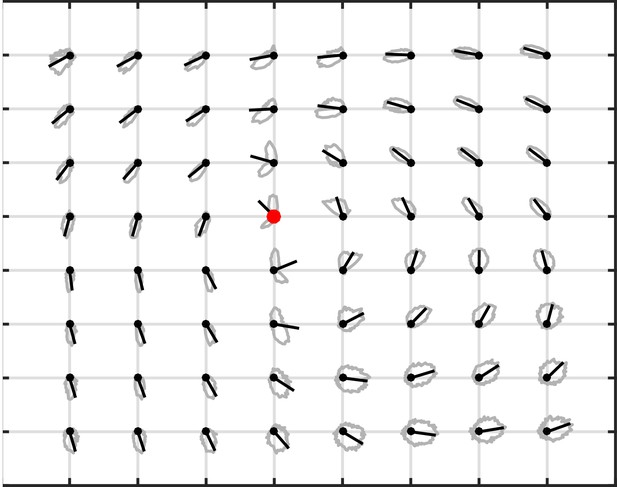
Vector field distribution control.
Distributions of phase gradient directions (gray lines) and circular mean direction of each distribution (black lines) are plotted relative to the rotation center (red dot) for all TPF wave cycles across subjects. The sharp distributions of phase gradient directions extend out to the edge of the electrode array, illustrating the global extent of the detected rotating waves.
Figure 1—figure supplement 7
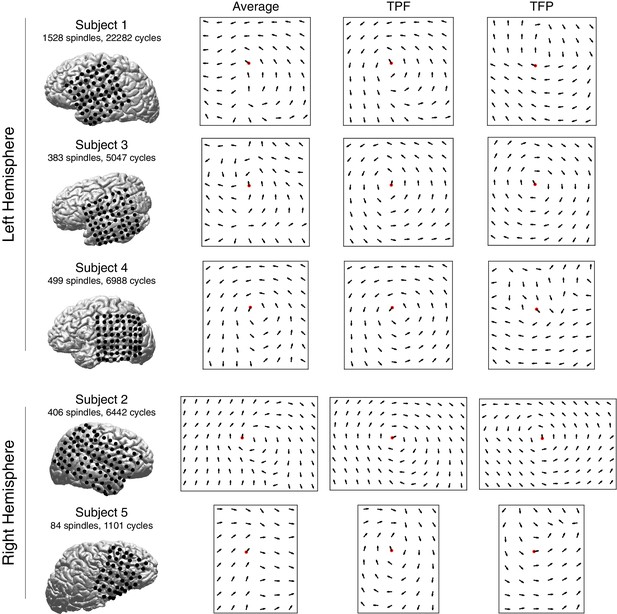
Vector field averages for each subject.
Average re-centered phase gradient directions over all spindle cycles in subjects 1–5. In each case, a rotational vector field indicates the robust spatiotemporal organization of rotating waves in a preferred direction (temporal parietal frontal cortex), in both right and left hemisphere electrode implantations (average). The two right columns for each subject depict average re-centered phase gradient directions for identified rotating waves in the TPF and TFP direction, respectively.
Figure 1—figure supplement 8
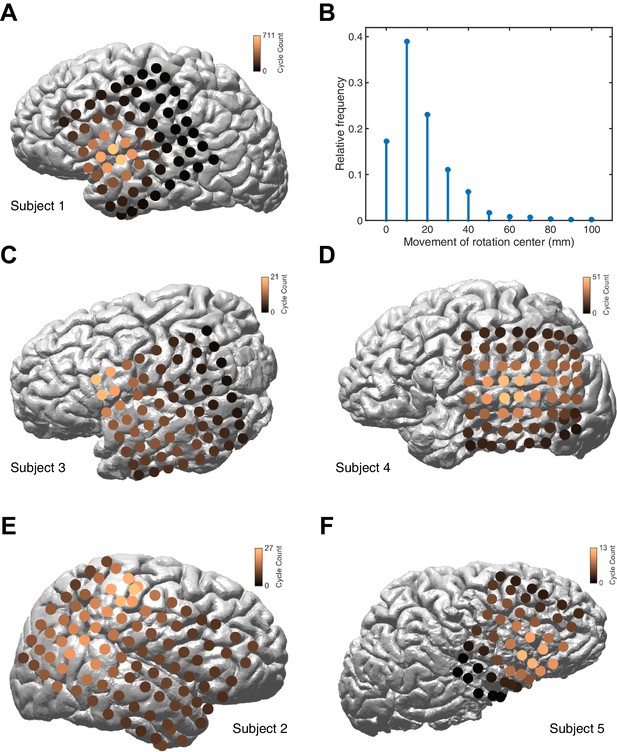
Distribution of rotation center.
(A) The distribution of rotation center is plotted on the cortical surface of Subject 1, for 10,944 rotating TPF waves. The distribution is concentrated around the dorsal temporal lobe, and centered on the Sylvian fissure. For this panel, a Gaussian smoothing with a standard deviation of 1 pixel has been applied. (B) The distribution of change in wave center for consecutive rotating TPF wave cycles in Subjects 1–5 illustrates that the rotating wave center changes slowly, if at all (cf. Video 1). (C–F) The distribution of rotation center for Subjects 2–5, plotted as in panel (A), illustrates approximately consistent anatomical localization of the TPF rotation center across subjects.
Figure 1—figure supplement 9
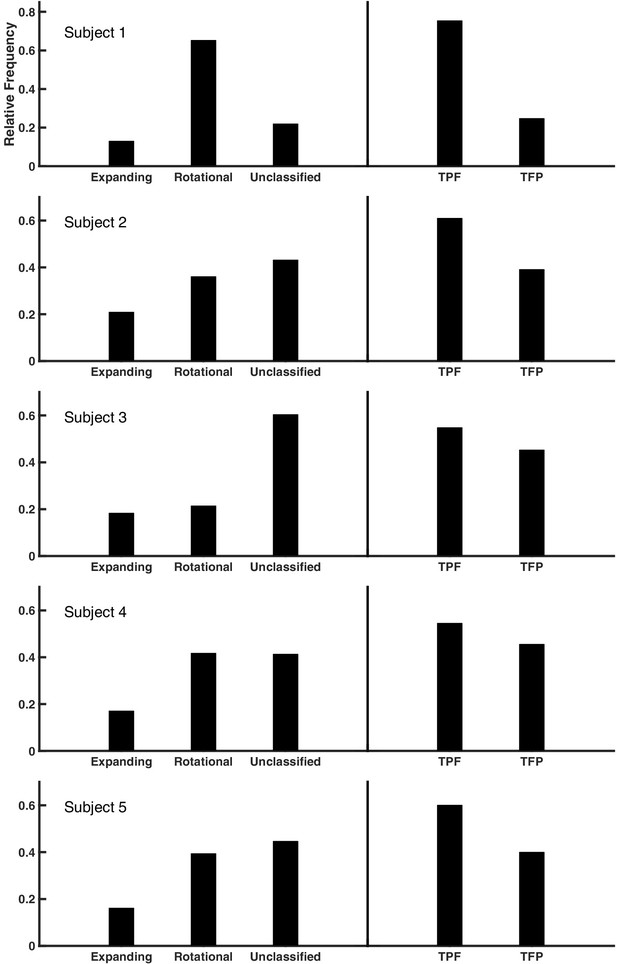
Summary statistics across subjects.
The proportion of expanding and rotational waves is given for subjects 1–5 (left), in addition to cycles unclassified by the detection algorithm. In each case, a rotational preference for the temporal parietal frontal (TPF) direction is present at the level of individual spindle oscillation cycles (right).
Figure 1—figure supplement 10
Consistent, coherent phase flow during spindles occurs uniquely in the 9–18 Hz frequency band.
Average re-centered phase gradient directions over all spindle cycles in three frequency bands (1–4 Hz, left; 9–18 Hz, center; 40–80 Hz, right) for subjects 1 (top row) and 2 (bottom row). In the 40–80 Hz frequency band, notch filtering in time was applied to remove the 60 Hz line noise. A clear pattern in the average directions emerges for the spindle frequency band, while the phase gradient direction maps in the other frequency bands are less clear.
Figure 1—figure supplement 11
Robustness to noise and center position.
Using simulated expanding and rotating waves, we verified the robustness of our detection approach under Gaussian white noise of varying amplitude. (A) Snapshots of simulated expanding waves in one oscillation cycle (at 85, 105, and 125 ms), under varying levels of noise (standard deviation 0, 0.1, and 0.2). (B) Simulated rotating waves, as in (A). (C) The performance of the algorithm in detecting expanding and rotational waves (blue and red solid lines, mean ± SEM), as compared to the thresholds derived from the permutation test (dotted lines). Every point represents 25 simulated spindles with 14 oscillation cycles each. Even when the noise standard deviation is unity (at parity with oscillation amplitude, highly obscuring visual detection), the algorithm recovers a correlation magnitude around 0.8 in each case, far above the determined permutation thresholds. In contrast, with only Gaussian white noise as input, the algorithm returns a low correlation value for rotational detection, below the determined permutation threshold (gray line). (D) Robustness of the algorithm to center position. This panel illustrates the performance of the algorithm for expanding (blue) and rotating (red) waves at different points on the electrode array, under Gaussian white noise (standard deviation 0.2). Note that performance drops for rotational detection at the border of the array, but this is small in comparison to the threshold determined from the permutation control (dotted red line).
Figure 1—figure supplement 12
Local versus global simulated rotating waves.
To test whether highly local spindles organized as traveling waves would be detected, we ran our algorithm on simulated global (64 electrodes) and local (6 electrodes, or 9.4% of the simulated array) rotating waves. (A) Each channel in the simulated waves had added noise similar to that observed in the data (top trace). Distal channels in the local waves had only noise (bottom trace). Note 100 ms scale bar in gray. (B) The correlation magnitude for the global wave (black line, mean + SEM) is high above the determined permutation threshold (dotted red line), while the correlation magnitude for the highly local wave (gray line) is well below. This control illustrates that finding high is indicative of a distributed and global phase pattern on the electrode array.
Figure 2
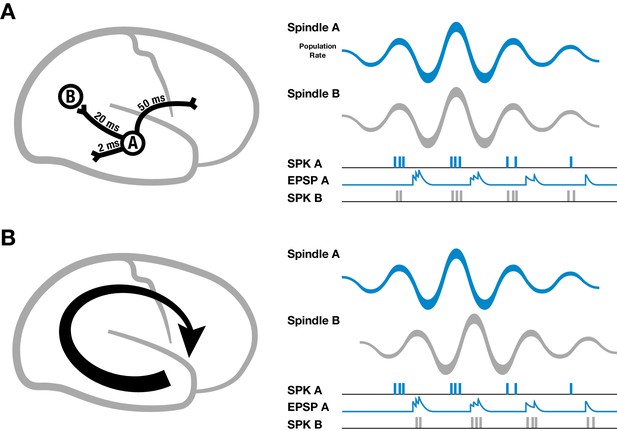
Schematic of spindles and axonal delays.
(A) Spikes emitted from region A will arrive at B with a temporal delay of 20 milliseconds (left). If spindle oscillations were perfectly synchronized across the cortex, EPSPs from region A would occur after the spikes in region B, within the window for long-term depression (right). (B) In contrast, if spindles are spatiotemporally organized with stereotyped trajectories (left), then EPSPs from region A would align with population spiking in region B, allowing for synaptic strengthening to occur.
Figure 3
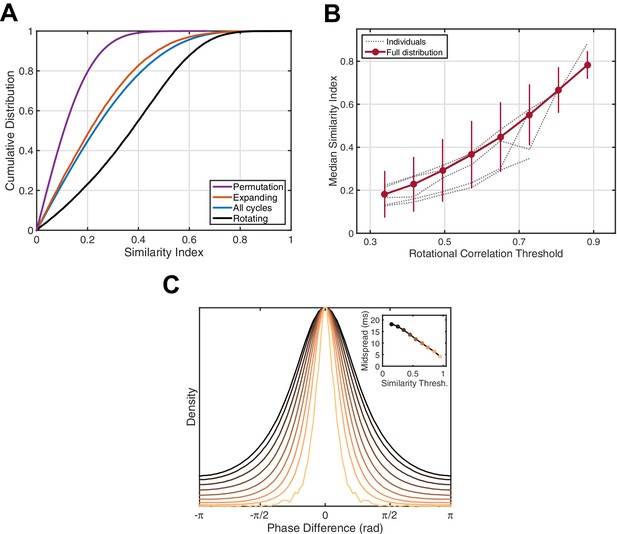
Phase pattern analysis.
(A) Rotating waves exhibit higher intra-class similarity. Cumulative distribution functions (CDFs) for shuffled data (purple), expanding waves (red), all cycles (blue), and rotating waves (black) are given for an example 15 min epoch of stage 2 sleep (subject 5). (B) Spindle cycles exhibiting stronger rotating patterns also express greater intra-class similarity. Gray lines indicate the median similarity index (ordinate) for the population of oscillation cycles expressing rotational waves above a threshold strength (abscissa), averaged over individual sleep epochs. Red dots and error bars indicate the median and median absolute deviation for the full distribution, respectively. (C) Spindle cycles exhibiting high similarity index are temporally precise. The distribution of phase difference at each electrode across spindle cycles is given as a function of the similarity index (indicated by colors, inset). By utilizing the mean spindle oscillation frequency (13.5 Hz), the midspread (interquartile range) of each distribution is given in units of time (inset).
Figure 4 with 3 supplements
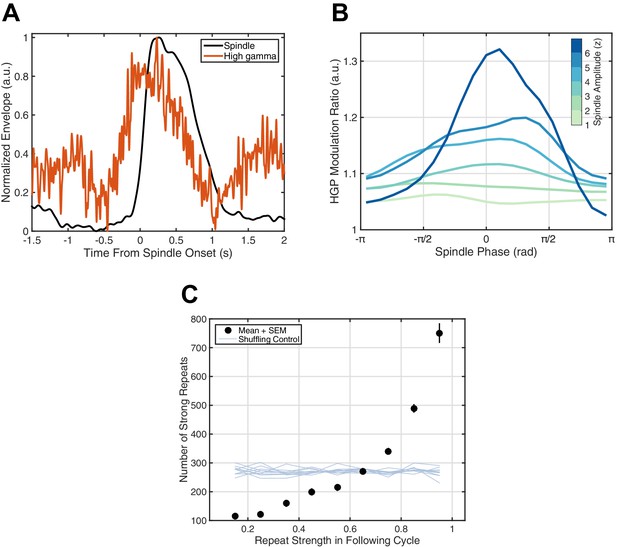
Spiking activity and increased reverberation.
(A) High gamma-band power (HGP) consistently increases around spindle onset. Plotted are the normalized amplitude envelopes for spindles (black) and HGP (red), averaged over 186 spindles in Subject 1. (B) HGP is modulated by spindle phase. Plotted is the mean high gamma-band power at each phase of the spindle oscillation (20 bins), for varying amplitudes of the spindle oscillation (see colorbar), each normalized by the mean HGP in matched non-spindle epochs. (C) Strength of the first repeat predicts the number of strong reverberations. The number of similar rotational patterns (above similarity index 0.7) following a spindle oscillation cycle is given as a function of the next cycle’s similarity index (black dots, mean + SEM) over 2.5 hr of sleep in Subject 1. Error bars are obscured by markers. Light blue lines indicate results from a shuffling permutation test (10 iterations).
Figure 4—figure supplement 1
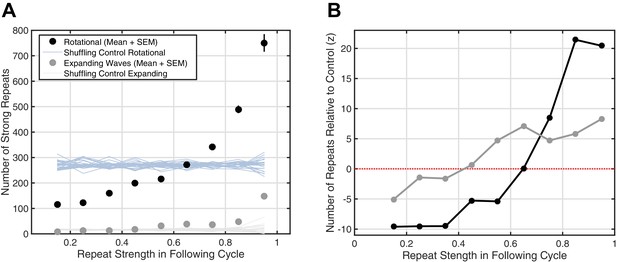
Strong increase of reverberation observed for rotating, but not expanding, waves.
(A) The increase in the number of strong repeats is given for expanding (gray dots, mean + SEM) and rotational (black dots) waves. Error bars are obscured behind the markers. Plotted also are the shuffling controls for rotating (light blue) and expanding (light gray) waves (25 iterations at each point). (B) The numbers of strong repeats in panel A are plotted as z-scores relative to the shuffling control distribution, for expanding (gray) and rotating (black) waves. This panel illustrates that the substantial, marked increase in reverberation is observed for rotating, but not expanding, waves.
Figure 4—figure supplement 2
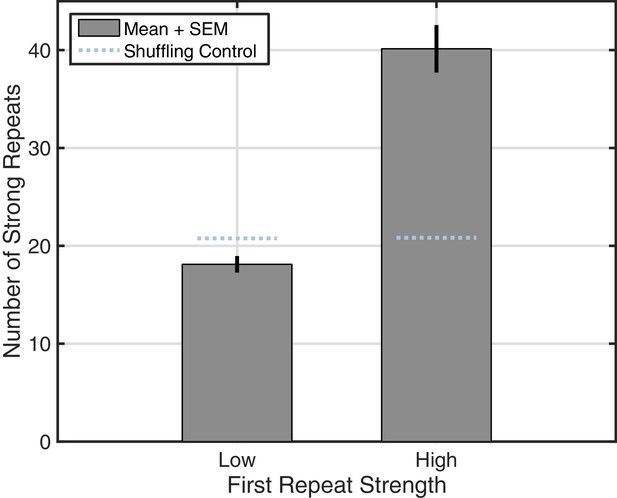
Increase in reverberation observed across subjects.
By aggregating data from shorter recordings in Subjects 2–5, we replicated the reverberation analysis (Figure 4C) using fewer bins (Low, less than 0.5 similarity index; high, greater than 0.5). Rotating wave patterns with a high-strength first repeat showed increased reverberation relative to the shuffling control (light blue dotted lines).
Figure 4—figure supplement 3
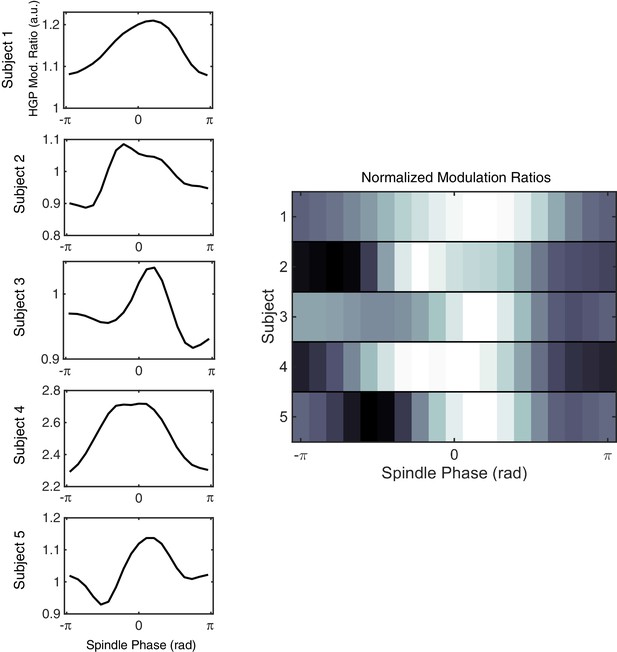
Modulation of high-gamma power (HGP) by spindle phase across subjects.
(Left) Mean HGP as a function of spindle phase is plotted for example stage 2 sleep epochs in Subjects 1–5. For this plot, spindle amplitudes above a given threshold (5 z-score units) were considered. As in Figure 4B, each plot is normalized by mean HGP in matched non-spindle epochs. (Right) Plotting each HGP modulation ratio normalized to its maximum (higher values in white) shows the consistent increase in HGP near the surface-positive (depth-negative) peak in each subject.
Videos
Video 1
Rotating waves over five spindle oscillation cycles.
Normalized activity for bandpass filtered timeseries is plotted in falsecolor at electrode positions on the cortical surface of Subject 1. The cortical electrode marked with a red dot (bottom) corresponds to the black timecourse in the inset (top). The other ECoG channels are plotted in gray. The time period visualized corresponds to approximately 300 milliseconds, or five cycles of the spindle oscillation. Note that no spatial smoothing is applied in these data.
Video 2
Rotating waves with high spatiotemporal similarity.
Two rotating waves with high phase similarity on the ECoG array, separated by 5.62 min of stage 2 sleep. Bandpass filtered timeseries are normalized to their maximum within the interval and plotted in falsecolor (bottom panels). Activity for each channel is plotted as a function of time (top panels), with an indication of temporal progression (red dotted line).
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Rotating waves during human sleep spindles organize global patterns of activity that repeat precisely through the night
eLife 5:e17267.
https://doi.org/10.7554/eLife.17267
