Figures and data in Ecological feedback in quorum-sensing microbial populations can induce heterogeneous production of autoinducers | eLife

Figures
Videos

7 figures and 3 videos

Figures

Figure 1

Download asset Open asset

The quorum-sensing model for the production of autoinducers in microbial populations.

(A) Sketch of a typical update step. Individuals are depicted as disks and the degree of autoinducer production ( $p_{i} \in [0, 1]$ ) is indicated by the size of the green fraction. Non-producers (orange disks) reproduce fastest, full producers (green disks) slowest. Individual $i$ with $p_{i} = 1 / 6$ divides into two offspring individuals, one of which replaces another individual $j$ . Both offspring individuals sense the average production level in the population ( $⟨ p ⟩ = 1 / 3$ ), and may either respond to this environment, with probability $λ$ , by adopting the value $R (⟨ p ⟩)$ of the response function ( $= 2 / 3$ here, see (B)) or, with probability $1 - λ$ , retain the production degree from the ancestor ( $= 1 / 6$ ). Here, offspring individual $i$ responds to the environment while $j$ does not (denoted by gray shading). (B) Quorum sensing is characterized by the response function. Perception of the average production level in the population ( $⟨ p ⟩$ ) enables individuals to change their production degree to the value $R (⟨ p ⟩) \in [0, 1]$ . Sketched are a monostable response function (stable fixed point at 1, unstable fixed point at 0), and a bistable response function (stable fixed points at 0 and 1, unstable fixed point at an intermediate threshold value). Stable fixed points of the response function are depicted as black circles while unstable fixed points are colored in white. For the sketched bistable response function, autoinducer production is down-regulated with respect to the sensed production level in the population below the threshold value, and up-regulated above this threshold. For the monostable response function, autoinducer production is up-regulated at all sensed production levels.

https://doi.org/10.7554/eLife.25773.003

Box 1—figure 1

Download asset Open asset

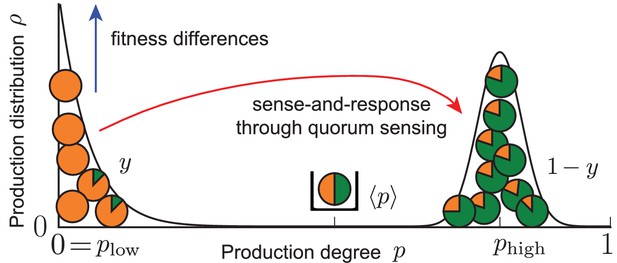
Effective picture of robust phenotypic heterogeneity through an ecological feedback.

The coupling of fitness differences between non-producers and producers (selection strength $s$ ) and sense-and-response to the self-shaped environment through quorum sensing (response probability $λ$ and up-regulation of production with response function $R (⟨ p ⟩)$ ) ensures the stable coexistence of the two subpopulations at the phenotypic states $p_{l o w}$ and $p_{h i g h}$ ; see Equation (2). The value $β = 2 λ / s$ quantifies this coexistence. In one subpopulation (fraction $y = 1 - β / R (β)$ of the total population), individuals do not produce ( $p_{l o w} = 0$ ), while in the other (fraction $1 - y$ ) individuals produce autoinducers to the degree $p_{h i g h} = R (β)$ . The average production level in the population is robustly adjusted to the value $⟨ p ⟩ = β$ . States of phenotypic heterogeneity arise for a broad range of initial distributions and are robust against noisy inheritance, noisy perception, and noisy response (see Results of mathematical analysis and Appendix 1—figures 1 and 2).

https://doi.org/10.7554/eLife.25773.005

Figure 2

Download asset Open asset

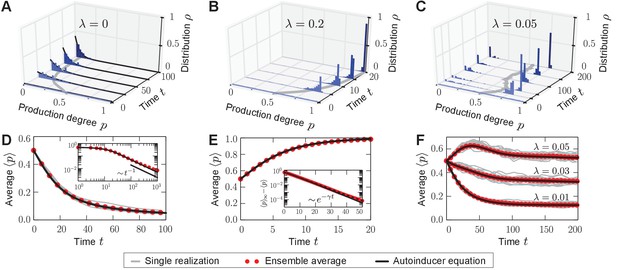
Homogeneous and heterogeneous production of autoinducers in the quorum-sensing model.

Temporal evolution of autoinducer production in the quorum-sensing model depicted as histograms of production degrees (normalized values), (A–C); and average production level of autoinducers in the population (D–F); see also Videos 1–3. (A) In the absence of sense-and-response ( $λ = 0$ ), only non-producers proliferate. The approach to stationarity is asymptotically algebraically slow for a quasi-continuous initial distribution of production degrees (D). The black line $⟨ p ⟩ \sim t^{- 1}$ serves as a guide for the eye. (B) Sense-and-response through quorum sensing ( $λ = 0.2$ here) promotes autoinducer production, and the population becomes homogeneous (ultimately, fixation at a single production degree, data not shown). The response function used here, $R (⟨ p ⟩) = ⟨ p ⟩ + 0.2 \cdot \sin (π ⟨ p ⟩)$ , was chosen such that an individual’s production degree is always up-regulated through quorum sensing (see Figure 1B). Approach to stationarity is exponentially fast (E), but timescales may diverge at bifurcations of the response function (see Appendix 1—figure 3). The dashed line in (E) shows fit to an exponential decay. (C) When $λ$ is small ( $λ = 0.05$ here), the population becomes heterogeneous: quasi-stationary states arise in which the population splits into two subpopulations, one of which does not produce autoinducers, while the other does. The same monostable response function was chosen as in (B). Therefore, heterogeneity may arise without bistable response. For very long times, one of the two absorbing states (A, B) is reached, data not shown (see Figure 3A). Heterogeneous, quasi-stationary states arise for a broad class of initial distributions (see Appendix 1—figure 1 and our mathematical analysis). At the same time, the average production level of autoinducers in the population is adjusted by the response probability $λ$ if $s$ is fixed (F) or vice versa (data not shown). Bimodal, quasi-stationary states also arise when noisy inheritance, noisy perception, and noisy response are included in the model set-up (see Appendix 1—figure 2). Mean-field theory agrees with all observations (autoinducer equation (1)). The time unit $Δ t = 1$ means that in a population consisting solely of non-producers, each individual will have reproduced once on average. Ensemble size $M = 100$ , $s = 0.2$ , $N = 10^{4}$ .

https://doi.org/10.7554/eLife.25773.006

Figure 2—source data 1 Source data accompanying Figure 2.: https://doi.org/10.7554/eLife.25773.007
Download elife-25773-fig2-data1-v1.zip

Figure 3

Download asset Open asset

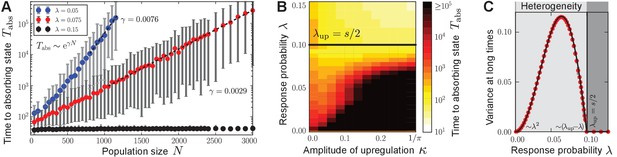
Characterization of phenotypic heterogeneity in the quorum-sensing model.

(A) For small response probability $λ$ , populations get stuck in heterogeneous quasi-stationary states. The time taken to reach a homogeneous absorbing state, $T_{a b s}$ , increases exponentially with the population size $N$ (filled circles denote the mean, gray bars denote the range within which 95% of the data points lie closest to the mean; dashed lines show fit to $T_{a b s} \sim e^{γ N}$ ). (B) Heterogeneous states are long-lived only if $λ$ is small and the response function is nonlinear (in particular, up-regulation is required for some average production level such that $R (⟨ p ⟩) > ⟨ p ⟩$ ). Here, the monostable response function $R (⟨ p ⟩) = ⟨ p ⟩ + κ \sin (π ⟨ p ⟩)$ was chosen such that $κ \in [0, 1 / π]$ scales the magnitude of up-regulation. As $κ$ increases, the gap between the low-productive and high-productive peaks of the heterogeneous state becomes larger such that it takes longer to reach the absorbing state. Mean-field theory (1) predicts the existence and local stability of heterogeneous stationary distributions for $0 < λ < λ_{u p} = s / 2$ (regime below the black line). Deviations between the stochastic process and mean-field theory are due to demographic fluctuations that vanish as $N \to \infty$ . (C) The variance of production degrees in the population reveals whether the population is in a homogeneous ( $Var (p) = 0$ ) or heterogeneous state ( $V a r (p) > 0$ ). The variance was averaged over long times in the quasi-stationary state. Mean-field theory (1) (black line) agrees with our numerical observations (red filled circles); see Methods and materials. Ensemble size $M = 100$ , $s = 0.2$ , in (B) $N = 10^{3}$ and in (C) $N = 10^{4}$ and $N = 5 \cdot 10^{4}$ close to $λ_{u p}$ , in (A, C) $κ = 0.2$ .

https://doi.org/10.7554/eLife.25773.011

Figure 3—source data 2 Source data accompanying Figure 3.: https://doi.org/10.7554/eLife.25773.012
Download elife-25773-fig3-data2-v1.zip

Appendix 1—figure 1

Download asset Open asset

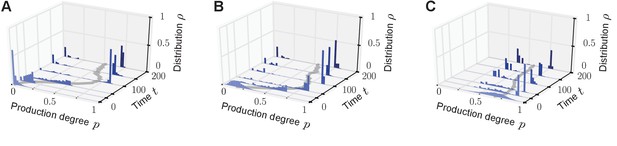
Phenotypic heterogeneity in the quorum-sensing model arises for diverse initial distributions.

Bimodal quasi-stationary states arise for a broad class of initial distributions if the value of the response probability $λ$ is small and an individual’s production degree is upregulated by the sense-and-response mechanism through quorum sensing ( $R (p) > p$ for some $p \in [0, 1]$ ). Depicted is the temporal evolution of the histograms of production degrees (normalized values) as in Figure 2 of the main text. The monostable response function $R (p) = p + 0.2 \cdot \sin (π p)$ was chosen (see Figure 1B). (A, B) $λ = 0.05$ . Initially, the population consists of mainly non-producers (in (A) initial distribution $p_{i} \sim B e t a (0.5, 20)$ i.i.d. and in (B) initial distribution $p_{i} \sim B e t a (4, 20)$ i.i.d.). Due to the balance of fitness differences and sense-and-response through quorum sensing, the population splits into a heterogeneous population with producers and non-producers coexisting for long times. (C) $λ = 0.02$ . If the initial distribution of production degrees is centered around high production degrees (initial distribution $p_{i} \sim B e t a (10, 5)$ i.i.d.), the population may still evolve in time into a heterogeneous quasi-stationary state. However, the peak at the low-producing degree is typically located away from 0, that is, $p_{l o w} > 0$ . These exemplary numerical results (A–C) are confirmed by the results of our mean-field theory: heterogeneous stationary distributions are the attractor of the mean-field dynamics (autoinducer equation (1) in the main text) for a broad range of initial distributions if conditions (i) $R ({\bar{p}}_{\infty}) = p_{h i g h} > {\bar{p}}_{\infty}$ and (ii) $λ < λ_{up} = s / 2$ are fulfilled (see main text). Note that ‘i.i.d.’ abbreviates ‘independent and identically distributed’. Parameters: selection strength $s = 0.2$ and population size $N = 10^{4}$ .

https://doi.org/10.7554/eLife.25773.013

Appendix 1—figure 2

Download asset Open asset

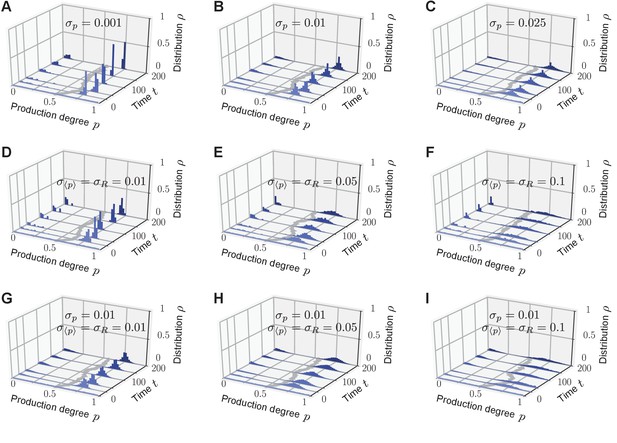
Phenotypic heterogeneity in the quorum-sensing model is robust against noisy inheritance, noisy perception, and noisy response.

Upon including either noisy inheritance of the production degree (A–C), or noisy perception of the average production level and noisy response to it (D–F), or both percx="">(G-I) into the model set-up, bimodal quasi-stationary states still arise in the relevant parameter regimes (see Figure 2C). Depicted are representative single realizations of the modified stochastic process (histogram over normalized values of production degrees to make the comparison with Figure 2 possible). (A–C) Noisy inheritance is implemented at reproduction events. Production degree $p_{i}$ is passed on to an offspring as $p_{i} \mapsto p_{i} + η_{p}$ with noise $η_{p} \sim 𝒩 (0, σ_{p})$ sampled from a Normal distribution (and are cut off such that $p_{i} + η_{p} \in [0, 1]$ ), emulating noisy inheritance of the phenotype. $σ_{p} \geq 0$ characterizes the strength of the noise ( $σ_{p} = 0$ recovers noiseless inheritance). As $σ_{p}$ increases, bimodal quasi-stationary states still arise, but the two peaks become broader than in the noiseless case. (D–F) Noise in the sensing apparatus is implemented as noisy perception of the average production level $⟨ p ⟩ \mapsto ⟨ p ⟩ + η_{⟨ p ⟩}$ with Gaussian noise $η_{⟨ p ⟩} \sim 𝒩 (0, σ_{⟨ p ⟩})$ , and noise in the response is implemented at the level of the response function as $R (⟨ p ⟩) \mapsto R (⟨ p ⟩) + η_{R}$ with Gaussian noise $η_{R} \sim 𝒩 (0, σ_{R})$ . Therefore, the production degree of an individual is updated through sense-and-response to the environment as $p_{i} = R (⟨ p ⟩) \mapsto R (⟨ p ⟩ + η_{⟨ p ⟩}) + η_{R}$ in the quorum-sensing model. Again, as the strength of both sense and response noise increase, bimodal quasi-stationary states still arise, but the two peaks become broadened compared with the noiseless case. We emphasize that $σ_{⟨ p ⟩} = σ_{R} = 0.1$ corresponds to very strong noise on the interval $[0, 1]$ . (G–I) Combined effect of noisy inheritance and noisy sense-and-response. Representative trajectories demonstrate that bimodal quasi-stationary states also arise in the presence of noise at all update steps. Thus, phenotypic heterogeneity in the quorum-sensing model is qualitatively robust against noise at all steps. Initial distribution: $p_{i} \sim U n i f o r m (0, 1)$ , independent and identically distributed; Parameters: selection strength $s = 0.2$ , response probability $λ = 0.05$ , response function $R (⟨ p ⟩) = ⟨ p ⟩ + 0.2 \cdot \sin (π ⟨ p ⟩)$ , and population size $N = 10^{4}$ .

https://doi.org/10.7554/eLife.25773.014

Appendix 1—figure 3

Download asset Open asset

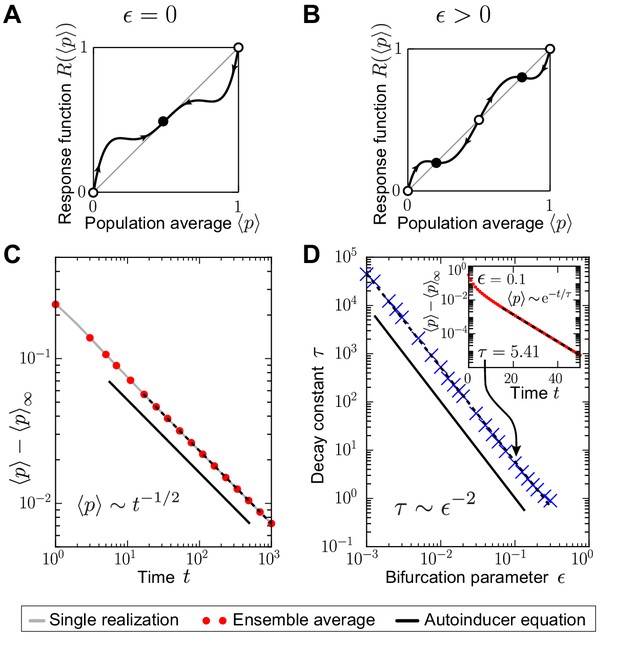
Time scales at which stationarity is approached may diverge.

The response probability was set to $λ = 1 / 2$ , and the nonlinear response function $R (⟨ p ⟩) = ⟨ p ⟩ + 40 \cdot ⟨ p ⟩ (⟨ p ⟩ - (0.5 - ϵ)) (⟨ p ⟩ - 0.5) (⟨ p ⟩ - (0.5 + ϵ)) (⟨ p ⟩ - 1)$ with bifurcation parameter $ϵ$ was chosen, see Equation (48); $ϵ$ controls a supercritical pitchfork bifurcation of the response function at the fixed point $p_{c r} = 0.5$ ( $R (p_{c r}) = p_{c r}$ ): For $ϵ > 0$ , the fixed point at $p_{c r}$ is unstable and non-degenerate (sketch in (B)), and becomes stable and threefold degenerate ( $z = 3$ ) as $ϵ = 0$ (sketch in (A)). (D) Away from the bifurcation of the response function ( $ϵ > 0$ ), the approach of an absorbing state in the stochastic many-particle system is exponentially fast (see inset of (D) for an exemplary measurement of $⟨ p ⟩ (t) - {⟨ p ⟩}_{\infty}$ for $ϵ = 0.1$ , dashed line denotes fit to exponential decay). The exponentially fast approach of stationarity is confirmed by mean-field theory ( ${\bar{p}}_{t} - {\bar{p}}_{\infty} \sim e^{- t / τ}$ ), see main text and Equation (51). Mean-field theory also predicts that the time scale of this exponentially fast relaxation diverges as $τ \sim ϵ^{- 2}$ as the bifurcation is approached ( $ϵ \to 0$ ), indicated by the black line in (D). This prediction agrees with the numerical simulations of the stochastic quorum-sensing model, see (D) (blue crosses denote values of the decay constants obtained from the exponential fits and black dashed line indicates fit to $τ \sim 1 / ϵ^{γ}$ with $γ = 1.95$ ). The divergence of time scales reflects critical slowing down as $ϵ \to 0$ . (C) At the bifurcation of the response function ( $ϵ = 0$ ), the approach of an absorbing state is algebraically slow, ${\bar{p}}_{t} - {\bar{p}}_{\infty} \sim t^{- 1 / ν}$ with critical exponent $ν = z - 1 = 2$ obtained from mean-field theory (black line), see Equation (53). This prediction agrees with our numerical simulations of the stochastic quorum-sensing model (black dashed line in (C) indicates fit to $⟨ p ⟩ (t) - {⟨ p ⟩}_{\infty} \sim t^{α}$ with $α = - 0.50$ ). Initial distribution: unimodal $p_{i} \sim B e t a (1, 10)$ , independent and identically distributed; Parameters: Ensemble size $M = 100$ , selection strength $s = 0.1$ , population size $N = 10^{4}$ .

https://doi.org/10.7554/eLife.25773.015

Videos

Video 1

Download asset

posterframe for video — Video accompanying Figure 2A – Homogeneous production of autoinducers in the population if sense-and-response is absent in the quorum-sensing model ( $λ = 0$ ).
https://doi.org/10.7554/eLife.25773.008

Video 2

Download asset

posterframe for video — Video accompanying Figure 2B – Homogeneous production of autoinducers in the population if sense-and-response is frequent in the quorum-sensing model ( $λ = 0.2$ here).
https://doi.org/10.7554/eLife.25773.009

Video 3

Download asset

posterframe for video — Video accompanying Figure 2C – Heterogeneous production of autoinducers in the population if sense-and-response is rare in the quorum-sensing model ( $λ = 0.05$ here).
https://doi.org/10.7554/eLife.25773.010

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Matthias Bauer
Johannes Knebel
Matthias Lechner
Peter Pickl
Erwin Frey

(2017)

Ecological feedback in quorum-sensing microbial populations can induce heterogeneous production of autoinducers

eLife 6:e25773.

https://doi.org/10.7554/eLife.25773

Sign up for email alerts

Privacy notice