Work minimization accounts for footfall phasing in slow quadrupedal gaits
- The Royal Veterinary College, United Kingdom
Figures
Figure 1
General relationships for walking quadrupeds between duty factor and limb phase following Hildebrand’s conventions for symmetrical gaits: duty factor defined as the proportion of the stride cycle in which a hind limb is in contact with the ground; limb phase the proportion of the cycle (as a %) after initial hindlimb contact that the forelimb of the same side makes contact.
Sloth relationship from (Nyakatura et al., 2010); Primate from (Cartmill et al., 2002). Points show values for a diverse range of quadrupedal species (Table 1), tentatively classified into two groups using K-means: Group 1 – high duty factor, phase 40–50% including reptiles, amphibians, mouse and hippo (grey points); Group 2 – the ‘normal mammalian’ grouping, with lower duty factor and phase around or somewhat below 25% (black points). The regression line relating to the presented points is: phase (%)=130 DF – 66. Phases greater than 80% are rarely if ever observed in steady, level gaits.
Figure 2
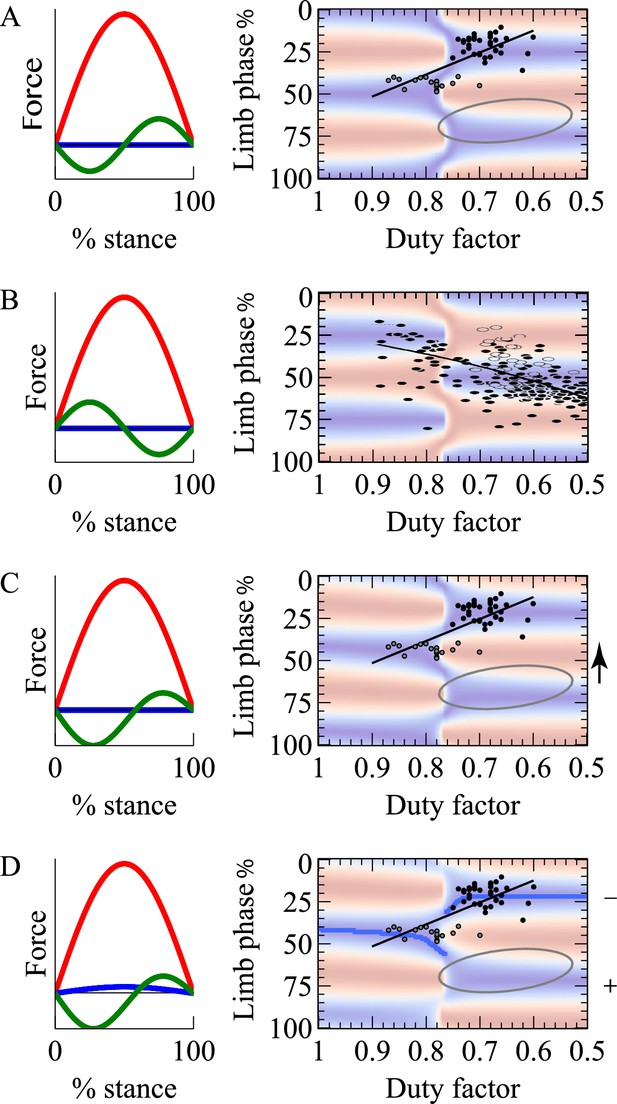
Model single limb forces (red vertical, green fore-aft, blue medial) and limb work cost surfaces (red high cost, blue low) for: (A) net-vertical limb impulses, and a cyclic decelerate-accelerate fore-aft force; (B) net-vertical limb impulses and a reversed fore-aft force profile modeling suspended, sloth-like progression; (C) inclined limb impulses, accelerating with the hindlimbs and decelerating with the fore (fore force trace shown); (D) as for (C) with the addition of a small medial impulse for each limb.
Overlying data (A, C, D) from a diverse range of quadrupedal species (see Figure 1), or only 2-toed sloth (B, [Nyakatura et al., 2010]). Overlying grey oval (A,C,D) denotes the region identified for primates by (Cartmill et al., 2002). Model C shifts the cost surface towards lower phases (arrow); Model D tips the surface, making higher phases more costly (denoted by +/−), and consequently the lower phase trough becomes the global minimum for each duty factor (dark blue line).
Figure 3
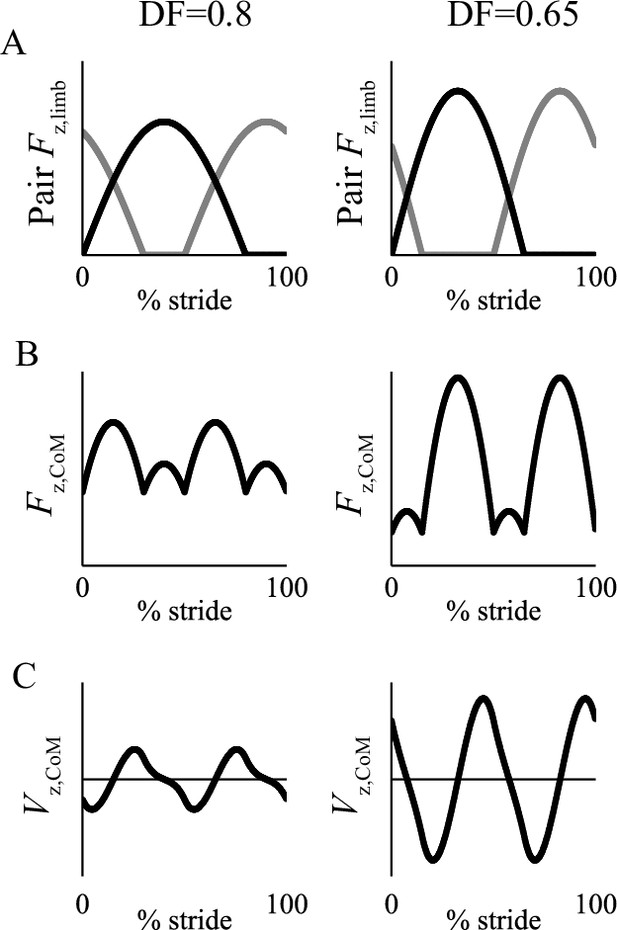
Graphical representation of the change of the relationship between vertical limb forces of diagonal pairs for a phase of 50% (trot timing) (A), center of mass forces (B) and center of mass velocities (C) due to high duty factor (0.8, suitable for Group 1) and low (0.65, Group 2).
At high duty factors, the vertical limb forces combine such that peak vertical force on the center of mass does not occur at the same time as the peak vertical limb force; consequently, whereas the vertical velocity of the center of mass is predominantly downward during the first half of stance in low duty factors, they are predominantly upward over the same period at high duty factors.
Figure 4
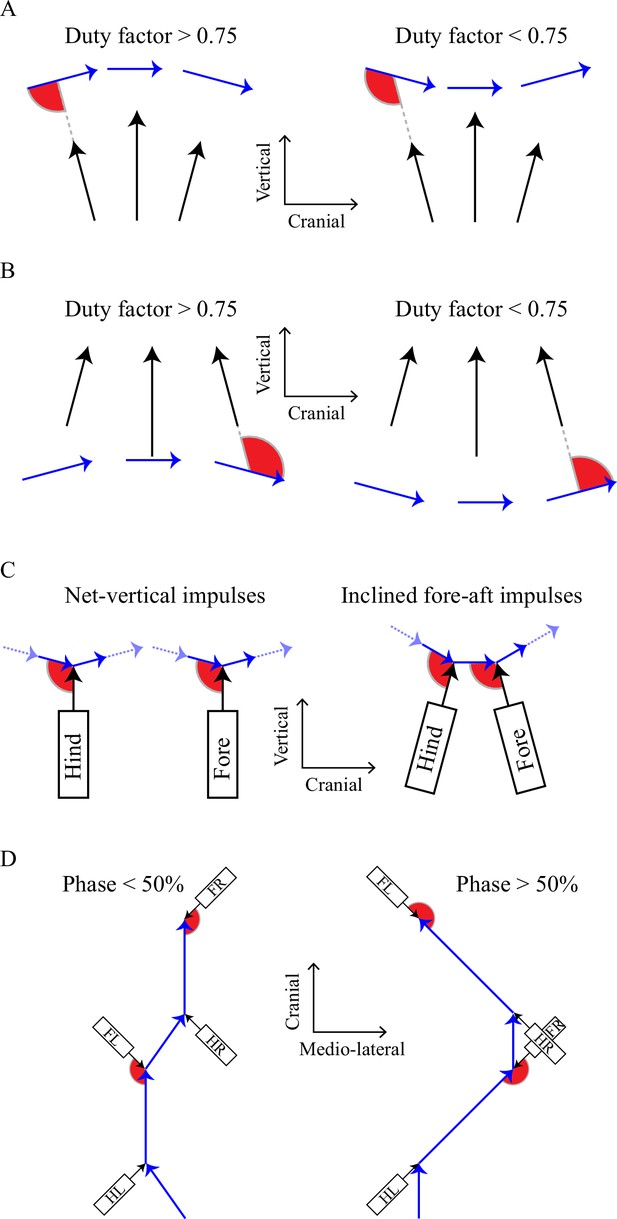
Geometric accounts for the cost surfaces found with the numerical model, highlighting the angle between limb forces or impulses (black arrows) and center of mass velocities.
Losses are lower if the angles (red wedges) between limb force (or impulse) and center of mass velocity vectors become closer to perpendicular. A): low mechanical work is demanded at 0/50% at high duty factors and 25/75% with low duty factors. B): the reversed relationship for sloths, in which horizontal forces profiles are reversed (see Figure 2B). In (A) and (B), force and velocity vectors are shown at snapshots in early, mid and late stance. 0% and 50% phasing (pace/trot timing) results in higher magnitude of center of mass vertical velocity, making the angle between limb force and center of mass velocity more nearly perpendicular at high duty factor (A), but at low duty factors for suspended, sloth-like gaits (B). C): the effect of inclined fore-aft impulses, demonstrated for low duty factors. Losses for purely vertical net impulses are minimized with even timing because changes in velocity vector are divided evenly; when the hind limbs impose net-acceleratory impulses (resisted by deceleration from the forelimbs), an even division of these collisions requires uneven phasing, reducing the period behind hind and fore contact (reducing the work-minimizing phase). D): a geometric account for the cost of high phases. Limb impulses (for left hind, LH, left fore, LF, right hind RH and right fore RF) and center of mass velocities are shown in the x-y plane (mediolateral/fore aft) for low and high phases. Again, angles between limb impulses and center of mass velocities are more favorable – closer to perpendicular – in the phase predicted to have lower cost by the numerical model. This is also consistent with lower fluctuations in speed (arrow length) – and so kinetic energy – for equivalent mean forward velocities.
Figure 5
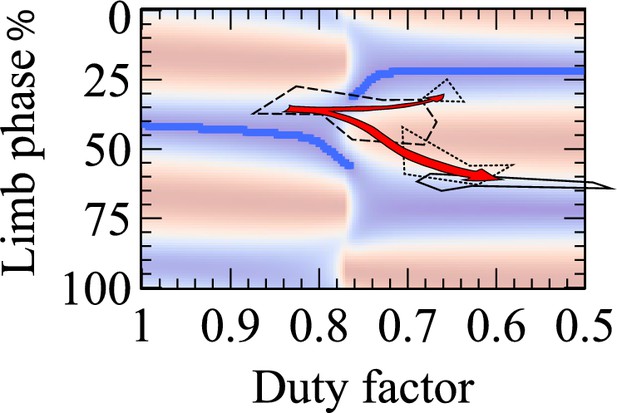
The final cost surface (blue low, red high, blue line indicating global minimum for each duty factor) overlain with Hildebrand’s measurements (Hildebrand, 1967) for a macaque (Macaca mulatta) through development.
Between 18 and 42 days (dashed line), high duty factors and phases close to 40% are observed. At 52 to 96 days (dotted lines), two regions are observed, before reaching the adult condition (solid line) typical of primates.
Tables
Table 1
See Supplementary file 1 for further information.
https://doi.org/10.7554/eLife.29495.003| Median duty factor | Median phase (%) | N | SD duty factor | SD phase (%) | |
|---|---|---|---|---|---|
| Group 1 | |||||
| Hamster* (Mesocricetus auratus) | 0.70 | 45 | 1 | ||
| Giant Salamander (Andrias japonicus) | 0.74 | 40 | 1 | ||
| Iguana (Iguana iguana) | 0.75 | 44 | 2 | 0.126 | 6.6 |
| Komodo Dragon (Varanus komodoensis) | 0.77 | 45 | 3 | 0.031 | 1.7 |
| Caiman (Caiman crocodilus) | 0.78 | 43 | 2 | 0.049 | 0.7 |
| Hippo (Hippopotamus amphibius) | 0.76 | 45 | 4 | 0.082 | 2.1 |
| Frog (Kassina maculata) | 0.78 | 44 | 1 | ||
| Bearded Dragon (Pogona vitticeps) | 0.78 | 48 | 1 | ||
| Crocodile (Crocodylus palustris) | 0.78 | 49 | 1 | ||
| Leopard Gecko (Eublepharis macularius) | 0.79 | 43 | 2 | 0.034 | 3.5 |
| Tiger Salamander (Ambystoma tigrinum) | 0.80 | 40 | 1 | ||
| Monitor Lizard (Varanus salvator) | 0.81 | 40 | 1 | ||
| Tortoise (Centrochelys sulcata) | 0.82 | 42 | 2 | 0.003 | 2.5 |
| Iguana (Conolophus pallidus) | 0.84 | 47 | 1 | ||
| Marine Iguana (Amblyrhynchus cristatus) | 0.85 | 41 | 1 | ||
| Mouse* (Mus musculus) | 0.86 | 40 | 1 | ||
| Alligator (Alligator mississippiensis) | 0.87 | 42 | 3 | 0.046 | 2.7 |
| Group 2 | |||||
| Mongoose (Mungos mungo) | 0.60 | 16 | 2 | 0.046 | 2.8 |
| Tapir (Tapirus indicus) | 0.61 | 26 | 1 | ||
| Rat (Rattus norvegicus) | 0.62 | 36 | 1 | ||
| Brown Bear (Ursus arctos) | 0.65 | 17 | 1 | ||
| Hyena (Crocuta crocuta) | 0.66 | 10 | 1 | ||
| Cat (Felis catus) | 0.66 | 21 | 2 | 0.060 | 3.7 |
| Pig (Sus domesticus) | 0.66 | 26 | 1 | ||
| Black Bear (Ursus americanus) | 0.67 | 18 | 1 | ||
| Horse (Equus caballus) | 0.67 | 24 | 2 | 0.015 | 1.1 |
| Zebra (Equus quagga) | 0.67 | 24 | 28** | 0.025 | 2.4 |
| Echidna (Tachyglossus aculeatus) | 0.67 | 13 | 1 | ||
| Polar Bear (Ursus maritimus) | 0.68 | 16 | 1 | ||
| Rhino (Ceratotherium simum) | 0.68 | 21 | 2 | 0.079 | 1.7 |
| Impala (Aepyceros melampus) | 0.68 | 19 | 1 | ||
| Lion (Panthera leo) | 0.68 | 15 | 3 | 0.017 | 1.5 |
| Sheep (Ovis aries) | 0.68 | 28 | 1 | ||
| Giraffe (Giraffa camelopardalis) | 0.68 | 14 | 5 | 0.030 | 1.4 |
| Cow (Bos taurus taurus) | 0.69 | 29 | 5 | 0.035 | 3.4 |
| Deer (Odocoileus virginianus) | 0.69 | 31 | 2 | 0.049 | 9.1 |
| Cheetah (Acinonyx jubatus) | 0.70 | 18 | 1 | ||
| Giant Anteater (Myrmecophaga tridactyla) | 0.70 | 27 | 1 | ||
| Tapir (Tapirus terrestris) | 0.70 | 26 | 1 | ||
| American Buffalo (Bison bison) | 0.71 | 16 | 1 | ||
| Bobcat (Lynx rufus) | 0.71 | 17 | 1 | ||
| Barbary Sheep (Ammotragus lervia) | 0.71 | 26 | 1 | ||
| Raccoon (Procyon lotor) | 0.71 | 14 | 1 | ||
| Goat (Capra aegagrus hircus) | 0.72 | 23 | 1 | ||
| Llama (Lama glama) | 0.72 | 17 | 1 | ||
| Camel (Camelus bactrianus) | 0.72 | 21 | 1 | ||
| Wildebeest (Connochaetes taurinus) | 0.72 | 18 | 11** | 0.017 | 1.6 |
| Donkey (Equus africanus asinus) | 0.73 | 25 | 1 | ||
| Elephant (Elephas maximus) | 0.73 | 19 | 1 | ||
| Wombat (Lasiorhinus krefftii) | 0.73 | 18 | 1 | ||
| Elephant (Loxodonta africana) | 0.74 | 17 | 4 | 0.026 | 1.3 |
| Porcupine (Erethizon dorsatum) | 0.75 | 29 | 2 | 0.051 | 0 |
Additional files
-
Supplementary file 1
All duty factor and phase data for walking quadrupeds, and their sources.
- https://doi.org/10.7554/eLife.29495.008
-
Transparent reporting form
- https://doi.org/10.7554/eLife.29495.009
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Work minimization accounts for footfall phasing in slow quadrupedal gaits
eLife 6:e29495.
https://doi.org/10.7554/eLife.29495
