Encoding sensory and motor patterns as time-invariant trajectories in recurrent neural networks
- University of California, Los Angeles, United States
Figures
Figure 1 with 1 supplement
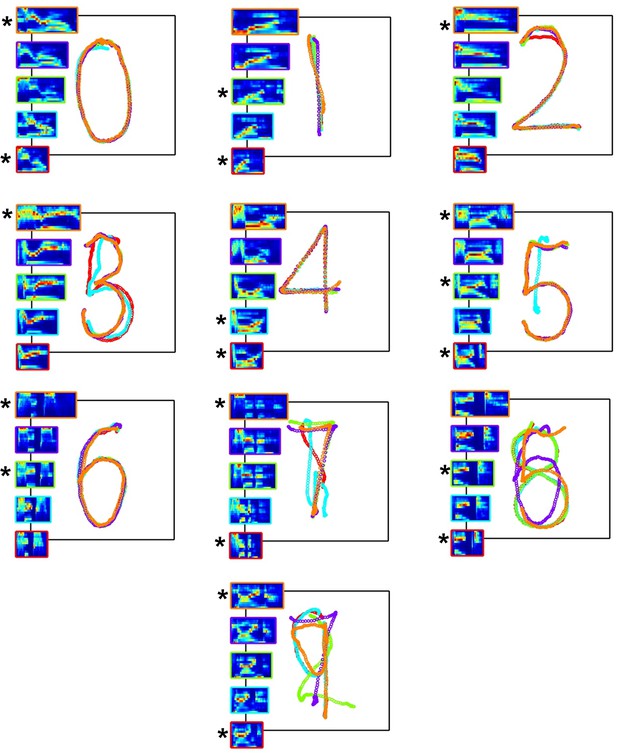
Trained RNNs perform a sensorimotor spoken-to-handwritten digit transcription task
(A) Transcription task. The spectrogram of a spoken digit, e.g. ‘two’, is transformed to a 12-channel cochleogram that serves as the continuous-time input to a RNN during the sensory epoch of each trial. During the motor epoch, the output units must transform the high-dimensional RNN activity into a low-dimensional ‘handwritten’ motor pattern corresponding to the spoken digit (the z output unit indicates whether the pen is in contact with the ‘paper’). The colors of the output pattern (right panel) represent time (as defined in the ‘Input’ panel). (B) Overlaid outputs of a trained RNN (N = 4000) for five sample utterances of each of 10 digits. For all digits, each output pattern is color-coded to the bounding box of the corresponding cochleogram (inset). Sample utterances shown are a mix of trained (*) and novel utterances, and span the range of utterance durations in the dataset. (C) Transcription performance of three different types of RNNs on novel utterances. Performance was based on images of the output as classified by a deep CNN handwritten digit classifier. The control groups include untrained RNNs (‘reservoir’) and RNNs trained only during the motor epoch (i.e., just to reproduce the handwritten patterns; see Figure 1—figure supplement 1). Output unit training was performed identically for all networks. Bars represent mean values over three replications, and error bars indicate standard errors of the mean. Line indicates chance performance (10%). The RNNs were trained on 90 utterances (10 digits, three subjects, three utterances per subject per digit). They were then tested on 410 novel utterances (across five speakers, including two novel speakers), with 10 test trials per utterance. I0 was set to 0.5 during network training (if applicable), and to 0.05 during output training and testing.
Figure 1—figure supplement 1
Transcription performance of an RNN trained only during the motor epoch.
Overlaid outputs of a motor-trained RNN (N = 4000) for five sample utterances of each of the 10 digits used in the spoken-to-handwritten digit transcription task. Transcription performance of the motor-trained RNN is poorer than its sensorimotor trained counterpart (Figure 1B). Each output pattern is color-coded to the bounding box of the corresponding cochleogram (insets). Sample utterances shown are a mix of trained (*) and novel utterances, and are the same ones shown in Figure 1B. The network was trained on 90 utterances (10 digits, three subjects, three utterances per subject per digit). I0 was set to 0.5 during network training, and to 0.05 during output training and testing.
Figure 2
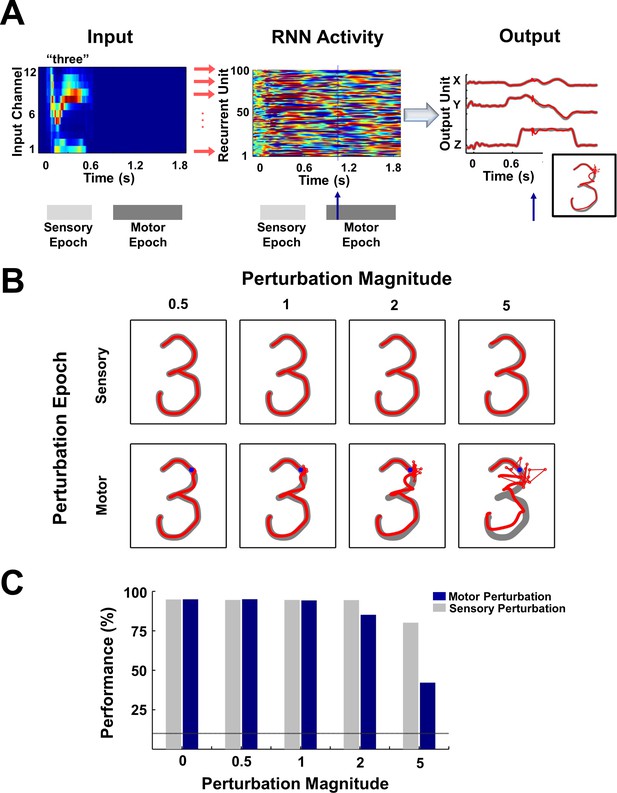
Digit transcription is robust to perturbations during the sensory and motor epochs.
(A) Schematic of a perturbation experiment. The motor trajectory of a trained RNN (N = 2100; 100 sample units shown) for the spoken digit ‘three’, is perturbed with a 25 ms pulse (amplitude = 2). The pulse (blue arrow) causes a disruption of the network trajectory, but the trajectory quickly recovers and returns to the dynamic attractor, as is evident from the plots on the right comparing the output unit values and the transcribed pattern for a trial with (red forefront) and without (gray backdrop) the perturbation. (B) Sample motor patterns generated by the network in response to perturbations of increasing magnitude, applied either during the sensory or motor epochs. Sensory epoch perturbations were applied halfway into the epoch, while motor epoch perturbations were applied at the 10% mark of the epoch (indicated by a blue dot). (C) Impact of perturbations on transcription performance (measured by the deep CNN classifier) for test utterances. Bars represent mean performance over ten trials, with a different (randomly selected) perturbation pulse applied at each trial. Line indicates chance performance. The performance measures establish that the encoding trajectories are stable to background noise perturbations, with transcription performance degrading gracefully as the perturbation magnitude increases. Furthermore, at all perturbation magnitudes, the sensory encodings are more robust than their motor counterparts due to the suppressive effects of the sensory input. The network was trained on 30 utterances (3 utterances of each digit by one subject) and tested on 70 (7 utterances of each digit by one subject). I0 was set to 0.25 during network training, to 0.01 during output training, and to 0 during testing except for the duration of the perturbation pulse.
Figure 3
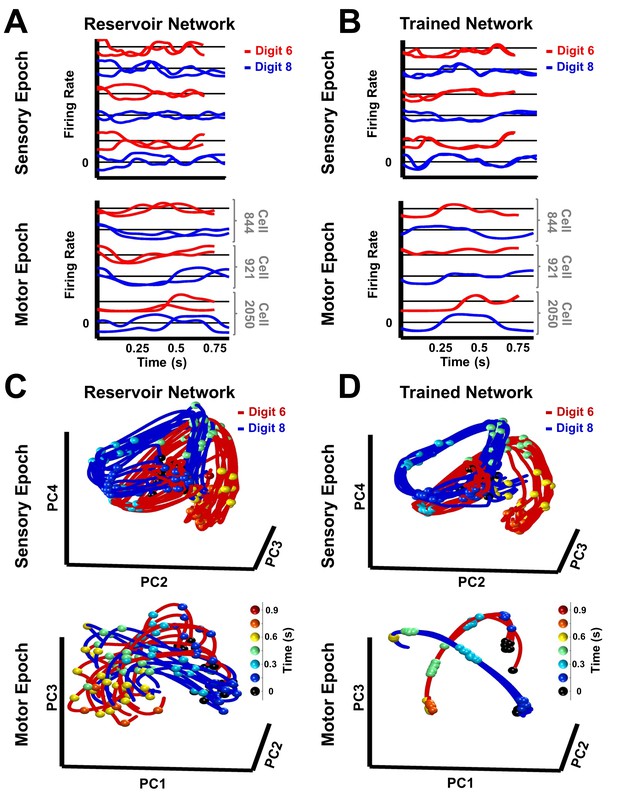
Trained RNNs generate convergent continuous neural trajectories in response to different instances of the same spatiotemporal object.
(A–B) Neural activity patterns of three sample units of a reservoir (A) and trained (B) network, in response to a trained and a novel utterance each of the digits ‘six’ (red traces) and ‘eight’ (blue traces) during the sensory (top) and motor (bottom) epochs. Utterances of similar duration were chosen for each digit, to allow for a direct comparison, without temporal warping, of the corresponding pair of sensory epoch traces. (C–D) Projections in PCA space of the sensory and motor trajectories for 10 utterances each of the digits ‘six’ and ‘eight’ generated by the reservoir (C) and trained (D) networks. Colored spheres represent time intervals of 150 ms. Compared to the reservoir network, in the trained RNN the activity patterns in response to different utterances of the same digit are closer, and the trajectories in response to different digits are better separated. Both networks were composed of 2100 units. Network training was performed with 30 utterances (one subject, 10 digits, three utterances per digit). I0 was set to 0.5 during network training, and to 0 while recording trajectories for the analysis.
Figure 4
Trained RNNs encode both sensory and motor objects as well separated neural trajectories.
(A) Euclidean distance between trajectories of the same digit (within-digit) versus those of different digits (between-digit). At each time step, the trajectory distances represent the mean and SD (shading) over pairs of one hundred utterances (one subject, 10 digits, 10 utterances per digit). During the sensory epoch, training brings trajectories for the same digit closer together, while maintaining a large separation between trajectories of different digits, thereby improving discriminability. A similar, but stronger, effect is observed during the motor epoch. (B) Comparison of the eigenspectrum of the recurrent weight matrix (WR) in a reservoir and trained network. Both networks were composed of 2100 units. Network training was performed with 30 utterances (one subject, 10 digits, three utterances per digit). I0 was set to 0.5 during network training, and to 0 while recording trajectories for the analysis.
Figure 5
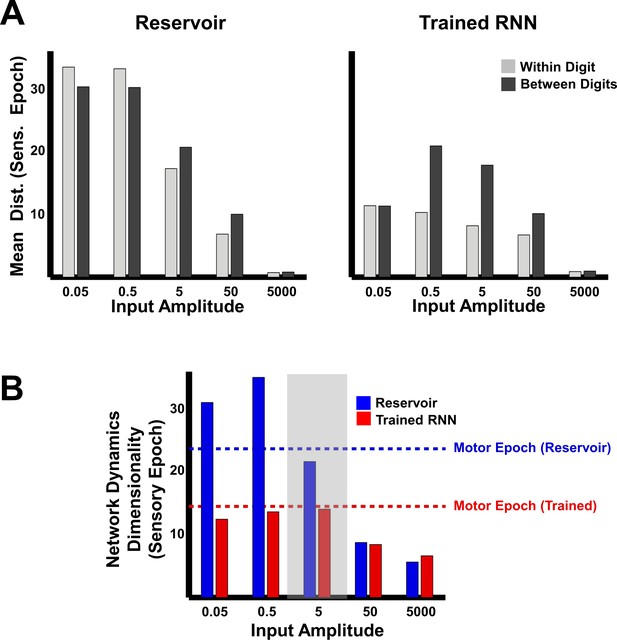
Trajectory separation in reservoir and trained RNNs as a function of input amplitude.
(A) Comparison of mean within- and between-digit distances of the sensory epoch trajectories in reservoir and trained networks (N = 2100) at different input amplitudes. Bars represent mean of the time-averaged distances for all utterances of all digits (one subject, 10 digits, 10 utterances per digit). (B) Dimensionality of sensory epoch trajectories in the reservoir and trained networks at different input amplitudes. Simulations, including training, in all other figures were performed at an input amplitude of 5 (gray highlight). Dashed lines indicate the dimensionality of the motor epoch trajectories in the reservoir (blue) and trained (red) networks, when the input amplitude was 5. Network training was performed with 30 utterances (one subject, 10 digits, three utterances per digit). The networks were trained with I0 set to 0.25, and trajectories were recorded with I0 set to 0.
Figure 6 with 1 supplement
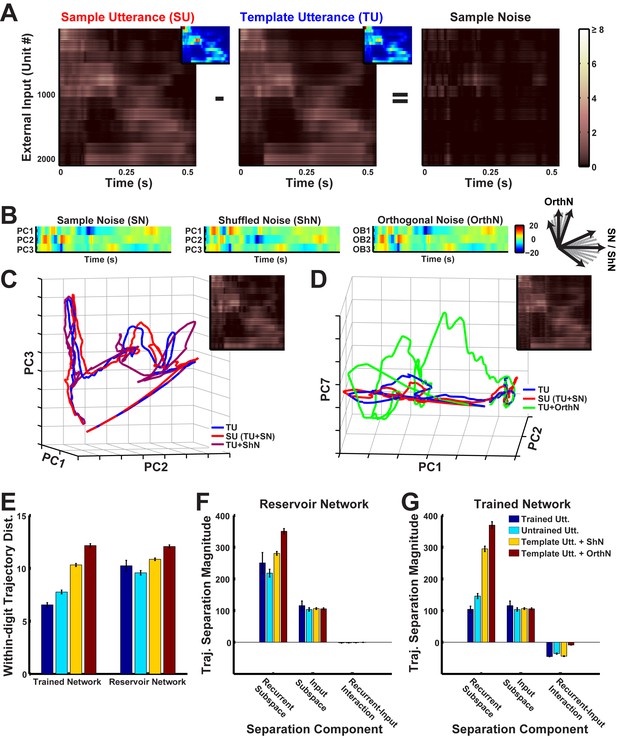
Robustness to spectral noise depends on the spatiotemporal structure of the inputs that the network is exposed to during training.
(A) Spectral noise in the inputs to an RNN (N = 2100) during presentations of digit zero. Sample noise is the difference between the external input (each row reflects net external input to a unit in the RNN) for a sample and template utterance (corresponding cochleogram inputs are shown as insets; see Materials and Methods for the definition of template utterance). Absolute values of external inputs are shown here for better visualization. (B) Coordinates of spectral noise in PCA space used to construct noisy utterances for digit zero. First three Principal component (PC) scores of the sample noise (left). Scores, where the basis was constructed as a random shuffle of the sample noise PC loadings (middle) and an orthonormal set orthogonal to the sample noise PC loadings (right). (C–D) Projections in PCA space of the external input for a template utterance, a sample utterance, and utterances with artificial noise created from the shuffled basis noise (C) and orthogonal basis noise (D). The respective artificial external inputs are shown as insets. (E) Comparison of mean within-digit distances of the trajectories for the different natural (two trained, blue and seven untrained, cyan) and artificial (30 shuffled, yellow and orthogonal, red each) utterances from the template utterance. Bars represent mean of the time-averaged distances for respective utterances of all digits (one subject, 10 digits). Error bars indicate standard errors of the mean over the digits. (F–G) Magnitudes of components that contribute to the total within-digit distance measured in (E) in the reservoir (F) and trained (G) networks. Bars represent mean of the time-averaged values of the components for respective utterances of all digits (one subject, 10 digits). Error bars indicate standard errors of the mean over the digits. The network was trained with I0 set to 0.25, and trajectories were recorded with I0 set to 0.
Figure 6—figure supplement 1
Schematic description of the decomposition of trajectories and trajectory separation into recurrent and input components.
(A) Left panel. Schematic of the evolution of a trajectory x(t). Right panel. The evolution of the trajectory in phase space between time steps t and t + 1 , can be decomposed into three component vectors: recurrent (red), input (green), and a passive component (black, which always points towards the origin). The sum of these vectors must equal the net movement of the trajectory between those time steps (see Materials and Methods for definitions of b and R). (B) Left panel. The total deviation between two trajectories x1(t) and x2(t) at time step t (Δx(t)), can be viewed similarly as being composed of the recurrent (ΔR(t)), input (ΔI(t)) and total (Δx(t-1)) deviations at time t-1. Right panel. The total deviation at t, in turn, can be decomposed into the recurrent and input deviations at the previous time steps (i.e. Equation S1 may be viewed as a recurrence relationship). Thus, the total deviation at t + 1 can be decomposed into recurrent and input deviation histories ( and , respectively, where the bar represents the exponentially weighted sum of the history up to time t). The vectors associated with ΔR and ΔI are plotted at different time points for visualization purposes.
Figure 7
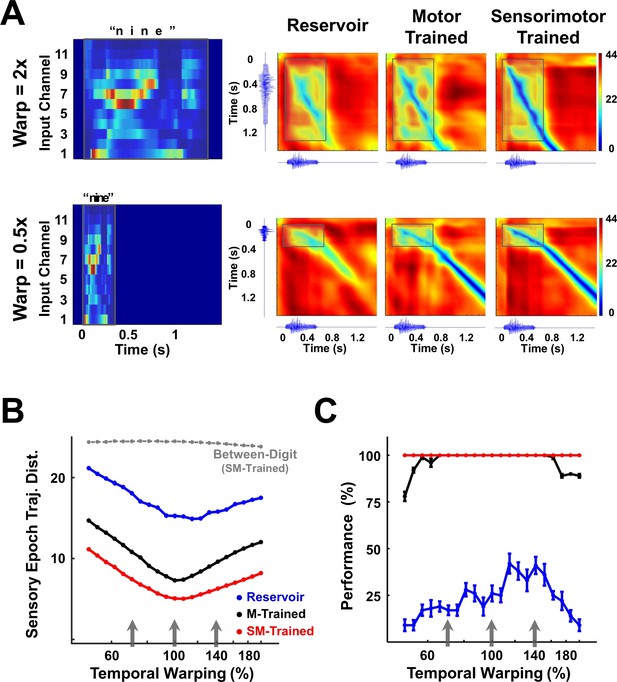
Invariance of encoding trajectories to temporally warped spoken digits.
(A) Temporally warped input cochleograms for an utterance of the digit ‘nine’ (left panel), warped by a factor of 2x (upper row) and 0.5x (lower row). Distance matrices between the trajectories produced by the warped and reference stimuli for the two control networks and the sensorimotor trained network (right panels). Distance matrices are accompanied by the corresponding sonograms on each axis, and highlight the comparison between the sensory trajectories of the warped and reference utterance (outlined box). A deep blue (zero-valued) diagonal through a distance matrix indicates that the sensory trajectory encoding the warped input overlaps with the reference trajectory. Thus, the sensorimotor trained RNN is more invariant (deeper blue diagonal) to temporal warping of the input than the motor-trained and reservoir RNNs. (B) Mean time-averaged Euclidean distance between sensory trajectories encoding warped and reference utterances of the 10 digits in each of the three networks, over a range of warp factors. Dashed gray line indicates mean distance between sensory trajectories encoding warped and reference utterances of different digits in the sensorimotor trained network. Error bars (not visible) indicate standard errors of the mean over 10 test trials. Gray arrows indicate the warp factors at which the networks were trained. (C) Transcription performance (measured by the deep CNN classifier) of the three networks on utterances warped over a range of warp factors. The results corroborate the measurements in (B) and show that a sensorimotor trained RNN is more resistant to temporal warping. All networks were composed of 2100 units. Network training was performed with 30 utterances (one subject, 10 digits, one utterance per digit, three warps per utterance). I0 was set to 0.25 during network training, and to 0.05 during output training and testing. Reference trajectories for the distance analysis were recorded with I0 set to 0.
Figure 8 with 2 supplements
Mechanism of temporal scaling invariance.
(A) Time-averaged linear speed (v) during the sensory epoch trajectories in the reservoir and trained networks (N = 2100) compared to the ideal linear speed, over a range of warp factors. The speeds are normalized to the 1x warp. (B) Schematic representation of two hypotheses for trajectories that exhibit temporal warp invariance via warp-dependent angular speeds (ω): constant linear speed/variable distance (green) and variable linear speed/constant distance (yellow) (C) Projections in PCA space of external input for warped utterances of digit one (left) and the corresponding sensory epoch trajectories of the trained network (right), over a 100 ms duration of the 1x warp trajectory and the corresponding utterance interval of the remaining trajectories. Over this short duration, over 90% of the variance in the external input and the trajectories was captured. (D) Mean linear speed (left) and cumulative distance traversed (time integral of the linear speed; right) in the recurrent subspace of phase space of a reservoir and trained network, compared to predictions from the constant speed and constant distance hypotheses. The measures are normalized to the 1x warp. In all panels error bars indicate SEM over the digits. The network was trained with I0 set to 0.25, and trajectories were recorded with I0 set to 0.
Figure 8—figure supplement 1
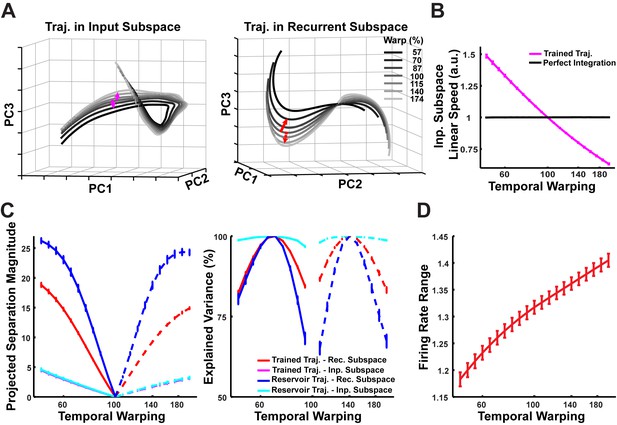
Phase space relationships in the input and recurrent subspaces as a function of the warp factor.
(A) Projections in PCA space of the input (left) and recurrent (right) subspace trajectories that compose the sensory epoch trajectories of a trained network (N = 2100), in response to warped utterances of digit one, over a 100 ms duration of the 1x warp trajectory and the corresponding utterance interval of the remaining trajectories. The contribution of the leaky integrated external inputs to the overall trajectory is termed the input subspace trajectory ( in Equation 4), and that of the recurrent dynamics is termed the recurrent subspace trajectory ( in Equation 4). While the external inputs are originally inseparable in phase space (Figure 8C), following integration by the RNN, these trajectories appear to separate out into parallel trajectories. A similar separation is observed in the recurrent subspace. (B) Time-averaged linear speed of sensory epoch trajectories in the input subspace of phase space where the inputs are leaky integrated (as in (A)), in comparison to the linear speed if the inputs were perfectly integrated. Whereas perfect integration produces constant speed trajectories (Figure 8B), leaky integration instead results in trajectories that are a balance of constant speed and constant distance. The speeds are normalized to the 1x warp. Error bars indicate standard errors of the mean over the digits. (C) Time-averaged within-digit separation of reservoir and trained sensory epoch trajectories at each warp factor, from the respective 1x warp trajectory, along a common time-dependent direction (left), establishes that they are parallel. Following temporal alignment, at each time step, the separation between a test trajectory and the corresponding 1x warp trajectory is projected onto the direction of separation between the 0.7x and 1x warp trajectories (solid), or the 1.4x and 1x warp trajectories (dashed), depending on the input warp factor for the test trajectory (directions indicated by arrows in (A)). Monotonically increasing separation from the 1x warp as a function of the input warp factor establishes that the trajectories are parallel over the manifold. The separation along these manifolds explains a majority of the variance in the overall separation of trajectories from the 1x warp trajectory (right), although the explained variance is lowest for the recurrent dynamics of the reservoir owing to its partially chaotic dynamics. Error bars indicate standard errors of the mean over the digits. (D) Mean range of recurrent unit firing rates (defined as ) during sensory epoch trajectories of the trained network, over a range of warp factors. Error bars indicate standard errors of the mean over the digits. The network was trained with I0 set to 0.25, and trajectories were recorded with I0 set to 0.
Figure 8—figure supplement 2
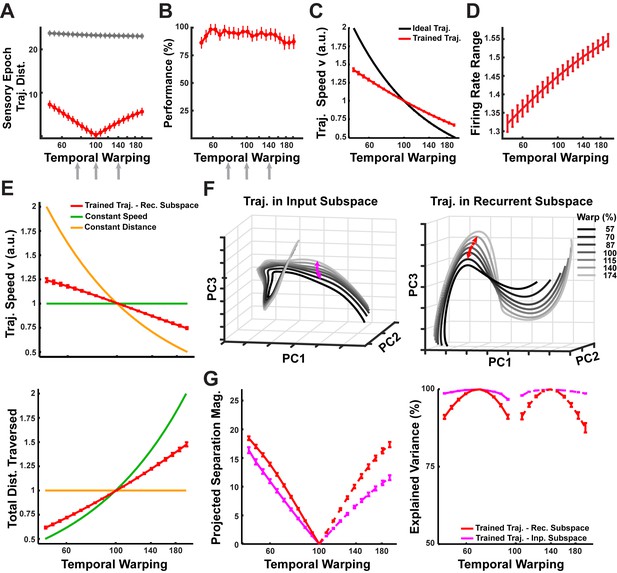
Temporal invariance performance and mechanism in a network trained with Backpropagation through time (BPTT).
(A) Mean time-averaged Euclidean distance between sensory trajectories encoding warped and reference utterances of the 10 digits, in a network trained with BPTT, over a range of warp factors. Dashed gray line indicates mean distance between sensory trajectories encoding warped and reference utterances of different digits. Error bars indicate standard errors of the mean over 10 test trials. End-to-end training of a 2100 unit network was performed on the transcription task with the BPTT algorithm applied via the ADAM optimizer (Materials and Methods), with a dataset of 30 artificially warped utterances as in Figures 7–8 (one subject, 10 digits, one utterance per digit, three warps per utterance). I0 was set to 0.25 during network training. Gray arrows indicate the warp factors at which the network was trained. (B) Transcription performance of the network (measured by the deep CNN classifier) on utterances warped over a range of warp factors. Error bars indicate standard errors of the mean over 10 test trials. The network exhibits good interpolation and extrapolation performance, but its overall performance is weaker than the network trained with ‘innate’ learning (Figure 7C). (C) Time-averaged linear speed of the sensory epoch trajectories in the BPTT trained network compared to the ideal speed, over a range of warp factors. The speeds are normalized to the 1x warp. (D) Mean range of recurrent unit firing rates (defined as ) during sensory epoch trajectories of the network, over a range of warp factors. Error bars indicate standard errors of the mean over the digits. (E) Mean linear speed (top) and cumulative distance traversed (time integral of the linear speed; bottom) in the recurrent subspace of phase space of the network, compared to predictions from the constant speed and constant distance hypotheses. The measures are normalized to the 1x warp. Error bars indicate SEM over the digits. (F) Projections in PCA space of the input (left) and recurrent (right) subspace trajectories that compose the sensory epoch trajectories of the trained network, in response to warped utterances of digit one, over a 100 ms duration of the 1x warp trajectory and the corresponding utterance interval of the remaining trajectories. (G) Time-averaged within-digit separation of the trained sensory epoch trajectories at each warp factor, from the respective 1x warp trajectory, along a common time-dependent direction (left), establishes that they are parallel. Following temporal alignment, at each time step, the separation between a test trajectory and the corresponding 1x warp trajectory is projected onto the direction of separation between the 0.7x and 1x warp trajectories (solid), or the 1.4x and 1x warp trajectories (dashed), depending on the input warp factor for the test trajectory (directions indicated by arrows in (F)). Monotonically increasing separation from the 1x warp as a function of the input warp factor establishes that the trajectories are parallel over the manifold. The separation along these manifolds explains a majority of the variance in the overall separation of trajectories from the 1x warp trajectory (right). Error bars indicate SEM over the digits. Network performance (panels A and B) was evaluated with I0 set to 0.05. Reference trajectories for the distance analysis (A) were recorded with I0 set to 0. Trajectories for panels (E) thru (F) were also recorded with I0 set to 0.
Videos
Video 1
A trained RNN performs the sensorimotor spoken-to-handwritten digit transcription task on novel utterances.
A trained RNN (N = 4000) and its output units perform the transcription task on five novel utterances (five different speakers). The last two utterances illustrate RNN performance on same-digit utterances of different durations (i.e. temporal invariance).Top Left: Input to the RNN (with audio). Moving gray bar indicates the current time step. Bottom Left: Evolution of RNN activity in a subset of the network (100 units). Right: Evolution of the output. The location of the pen is imprinted in red when the z co-ordinate is greater than 0.5, and plotted in gray otherwise.
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.31134.015
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Encoding sensory and motor patterns as time-invariant trajectories in recurrent neural networks
eLife 7:e31134.
https://doi.org/10.7554/eLife.31134
