The lawful imprecision of human surface tilt estimation in natural scenes
- University of Pennsylvania, United States
Figures
Figure 1
Tilt and slant, natural scene database, and tilt prior.
(A) Tilt is the direction of slant. Slant is the amount of rotation out of the reference (e.g., frontoparallel) plane. (B) Example stereo-image pair (top) and corresponding stereo-range data (bottom). The gauge figure indicates local surface orientation. To see the scene in stereo 3D, free-fuse the left-eye (LE) and right-eye (RE) images. (C) Prior distribution of unsigned tilt in natural scenes, computed from 600 million groundtruth tilt samples in the natural scene database (see Materials and methods). Cardinal surface tilts associated with the ground plane (90°) and tree trunks (0° and 180°) occur far more frequently than oblique tilts in natural scenes. Unsigned tilt, , indicates 3D surface orientation up to a sign ambiguity (i.e., tilt modulo 180°).
Figure 2 with 5 supplements
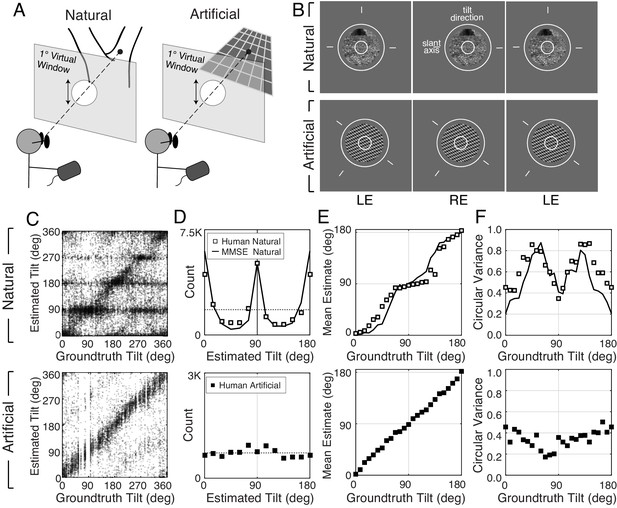
Experimental stimuli and human tilt responses.
(A) The virtual viewing situation. (B) Example natural stimulus (ground plane) and artificial stimulus (3.5cpd plaid). See Figure 2—figure supplement 3 for all three types. The task was to report the tilt at the center of the small (1° diameter) circle. Aperture sizes were either 3° (shown) or 1° (not shown) of visual angle. Observers set the orientation of the probe (circle and line segments) to indicate estimated tilt. Free-fuse to see in stereo 3D. (C) Raw responses for every trial in the experiment. (D) Histogram of raw responses (unsigned estimates). The dashed horizontal line shows the uniform distribution of groundtruth tilts presented in the experiment. (Histograms of signed tilt estimates are shown in Figure 2—figure supplement 4.) (E) Estimate means and (F) estimate variances as a function of groundtruth tilt. Human tilt estimates are more biased and variable with natural stimuli (top) than with artificial stimuli (bottom). Data are combined across all three artificial texture types; see Figure 2—figure supplement 3 for performance with each individual texture type. With artificial stimuli, human estimates are unbiased and estimate variance is low. Model observer predictions (minimum mean squared error [MMSE] estimates; black curves) parallel human performance with natural stimuli.
Figure 2—figure supplement 1
Tilt estimation errors with small vs. large apertures for natural stimuli.
Signed tilt is defined in with slant in [0°,90°); unsigned tilt is defined in [0°,180°) and slant in [−90°,90°). Estimation errors are analyzed in both the signed tilt and in the unsigned tilt domain. To reduce the possibility that individual stimuli were memorized, sessions with small apertures always preceded sessions with large apertures for a given set of natural stimuli. (A) Mean absolute error in the signed tilt domain across trials in each of 24 experimental sessions. The 3° aperture improves signed tilt estimation performance. With a 1° aperture, humans make significantly more sign mistakes (e.g., estimating a tilt of 45° when the groundtruth tilt is 225°). (B) Mean absolute error in the unsigned tilt domain across trials in each of 24 experimental sessions. Errors with large and small apertures in the unsigned domain are nearly indistinguishable. (C) Unsigned trial-by-trial errors with small vs. large windows for each human observer. The errors are strongly correlated, although there are several examples of 90° shifted estimates in the data of Humans 1 and 3. Overall, with unsigned tilt, performance with small and large windows was nearly equivalent.
Figure 2—figure supplement 2
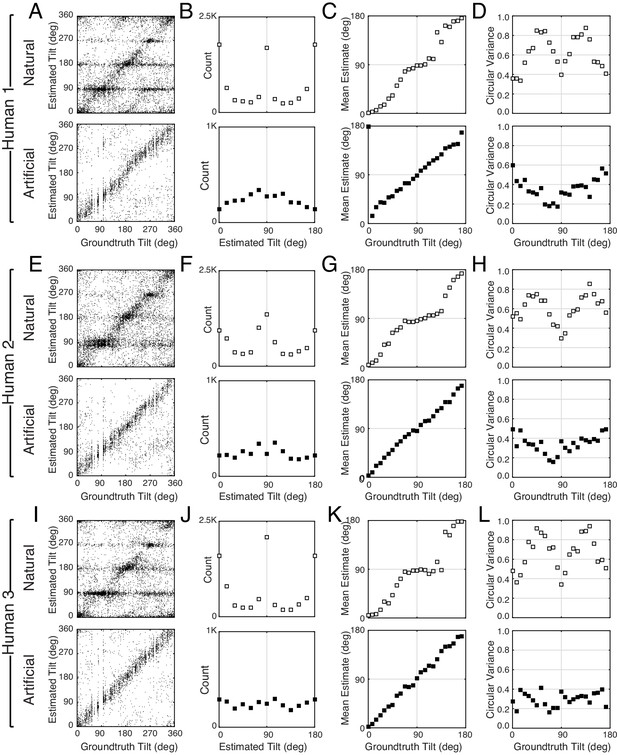
Tilt estimation performance for individual human observers.
(A) Raw tilt responses from Human 1, represented in the signed tilt domain , for natural and artificial stimuli. (B) Histogram of raw responses (estimates) in the unsigned domain . (C) Mean estimates and (D) estimate variance as a function of groundtruth tilt. (E–H) Same as A–D but for Human 2. (I–L) Same as A–D but for Human 3.
Figure 2—figure supplement 3
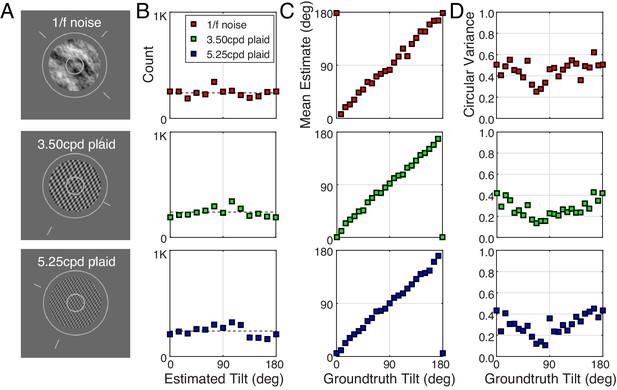
Summary statistics for the three different artificial stimulus types: 1/f noise, 3.50 cpd plaid, 5.25 cpd plaid (top, middle, and bottom rows, respectively).
Estimate variance for 1/f noise texture artificial stimuli is slightly higher than estimate variance with the plaids. The patterns are otherwise similar.
Figure 2—figure supplement 4
Histogram of raw responses (estimates) from human observers in the signed tilt domain .
The dashed line represents the uniform distribution of tested stimuli. (A) Human responses to natural stimuli. The distribution peaks at cardinal angles, but the peak at 270° is significantly lower than the peak at 90°, similar to the distribution of tilts in natural scenes computed directly from the database. (B) Human responses to artificial stimuli are more similar to the distribution of tested tilts. (C) Prior probability distribution of groundtruth tilts, computed directly from the natural scene database, in the signed tilt domain.
Figure 2—figure supplement 5
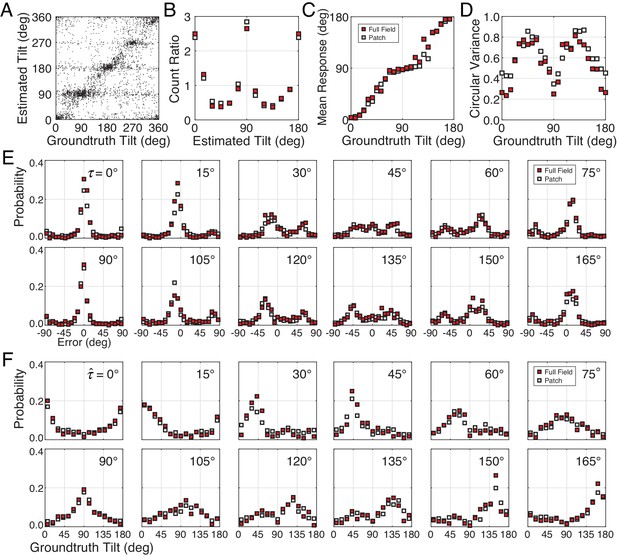
Tilt estimation performance with full-field (36° x 21°) viewing of natural stimuli.
Estimates were obtained for half the natural stimuli in the main experiment (1800 trials) from two of the three human observers. The experimental design was otherwise the same as the original experiment. (A) Raw responses. (B) Count ratio of estimates for full-field viewing (red) and the data from the main experiment (white). (C) Mean estimates as a function of groundtruth tilt. (D) Estimate variance as a function of groundtruth tilt. (E) Distribution of estimation errors for different groundtruth tilts. (F) Distribution of groundtruth tilt for different tilt estimates.
Figure 3
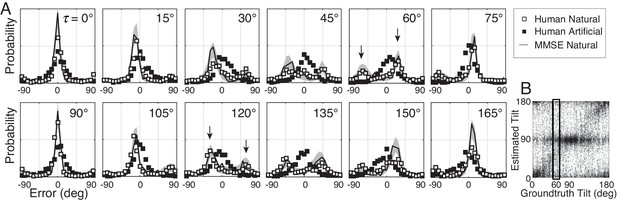
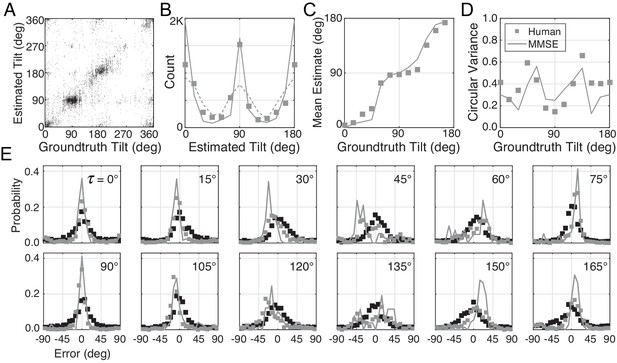
Distribution of tilt estimation errors for different groundtruth tilts.
(A) Conditional error distributions are obtained by binning estimates for each groundtruth tilt (vertical bins in Figure 3B) and subtracting the groundtruth tilt. With artificial stimuli, the error distributions are centered on 0° (black symbols). With natural stimuli, the error distributions change systematically with groundtruth tilt (white symbols). For cardinal groundtruth tilts (0° and 90°), the most common error is zero. For oblique tilts, the error distributions peak at values other than zero (e.g., arrows in and subplots). The irregular error distributions are nicely predicted by the MMSE estimator (black curve); shaded regions show 95% confidence intervals on the MMSE estimates from 1000 Monte Carlo simulations of the experiment (see Materials and methods). The MMSE estimator predicts human performance even though zero free parameters were fit to the human responses. (B) Raw unsigned tilt estimates with natural stimuli (same data as Figure 2C, but shown in the unsigned tilt domain). The rectangular box shows estimates in the tilt bin.
Figure 4 with 1 supplement
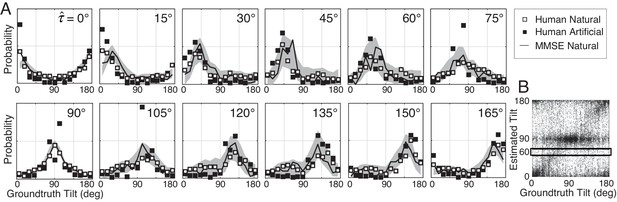
Distribution of groundtruth tilts for different tilt estimates.
(A) Conditional distributions of groundtruth tilt are obtained by binning groundtruth tilts for each estimated tilt (horizontal bins in Figure 4B). Unlike the conditional error distributions, these distributions are similar with natural and artificial stimuli. The most probable groundtruth tilt, conditional on the estimate, peaks at the estimated tilt for both stimulus types. Thus, any given estimate is a good indicator of the groundtruth tilt despite the overall poorer performance with natural stimuli. Also, these conditional distributions are well accounted for by the MMSE estimates; shaded regions show 95% confidence intervals on the MMSE estimates from 1000 Monte Carlo simulations of the experiment (see Materials and methods). The MMSE model had zero free parameters to fit to human performance. (B) Raw unsigned tilt estimates (same data as Figure 2C, but shown in the unsigned tilt domain). The box shows groundtruth tilts in the estimated tilt bin.
Figure 4—figure supplement 1
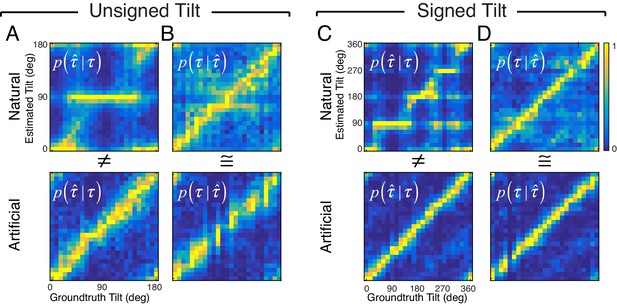
Alternative visualization of data in Figures 3 and 4.
Top row: Natural stimuli. Bottom row: Artificial stimuli. (A) Conditional probability of estimated tilts given groundtruth tilt in the unsigned tilt domain: [0, 180°). Each column of each subplot represents the conditional probability distribution of estimates for a different groundtruth tilt. Hence, each column represents the data in each subplot of Figure 3. (B) Conditional probability of groundtruth tilts given estimated tilt. Each row of each subplot represents the conditional probability distribution of groundtruth tilts for a different estimate. Hence, each row represents the data in each subplot of Figure 4. (C,D) Same as (A,B) but in the signed tilt domain: [0°, 360°). For visualization, each conditional probability distribution is normalized so that the maximum probability equals 1.0 (colorbar). The distributions of tilt estimates from natural and artificial stimuli conditional on groundtruth tilts are very different (A,C). By contrast, the distributions of groundtruth tilts conditional on estimates from natural and artificial stimuli are very similar (B,D). Thus, regardless of the stimulus type, the information provided about groundtruth by human tilt estimates is of similar quality. This property of the estimates should simplify subsequent processing that combines local into more global estimates (see main text).
Figure 5 with 1 supplement
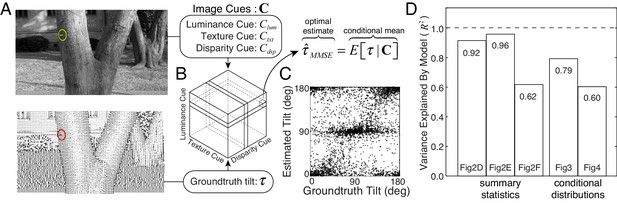
Normative model for tilt estimation in natural scenes.
(A) The model observer estimate is the minimum mean squared error (MMSE) tilt estimate given three image cue measurements. Optimal estimates are approximated from 600 million data points (90 stereo-images) in the natural scene database: image cue values are computed directly from the photographic images and groundtruth tilts are computed directly from the distance data. (B) MMSE estimates for ~260,000 (643) unique image cue triplets are stored in an ‘estimate cube.’ (C) Model observer estimates for the 3600 unique natural stimuli used in the experiment. For each stimulus used in the experiment, the image cues are computed, and the MMSE estimate is looked up in the ‘estimate cube.’ Excluding the 3600 experimental stimuli from the 600 million stimuli that determined the estimate cube has no impact on predictions. The optimal estimates within the estimate cube change smoothly with the image cue values; hence, a relatively small number of samples can explore the structure of the full 3D space and provide representative performance measures (see Discussion). (D) Proportion variance explained () by the normative model for the summary statistics (estimate counts, means, and variances; Figure 2D–F) and the conditional distributions (Figures 3 and 4). All values are highly significant ().
Figure 5—figure supplement 1
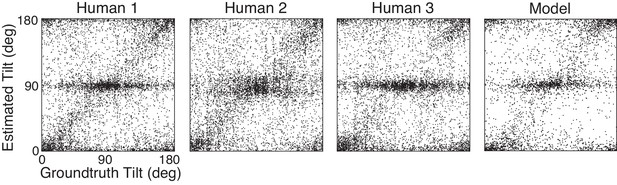
Unsigned tilt estimates: human observers and normative model.
Each panel shows the unsigned tilt estimate of a human or model observer plotted against the groundtruth tilt of every stimulus presented in the experiment.
Figure 6 with 2 supplements
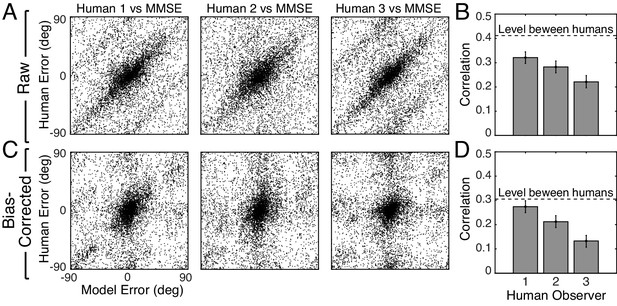
Trial-by-trial estimation errors: normative model vs. human observers.
The diagonal structure in the plots indicates that trial-by-trial errors are correlated. (A) Raw trial-by-trial errors with natural stimuli between model and human observers. (B) Correlation coefficients (circular) for trial-by-trial errors between model and each human observer. The error bars represent 95% confidence intervals from 1000 bootstrapped samples of the correlation coefficient. The dashed line shows the mean of the correlation coefficients of errors between human observers in natural stimuli (Figure 6—figure supplement 1). (C) Bias-corrected errors in natural stimuli. (D) Correlation coefficient for bias-corrected errors.
Figure 6—figure supplement 1
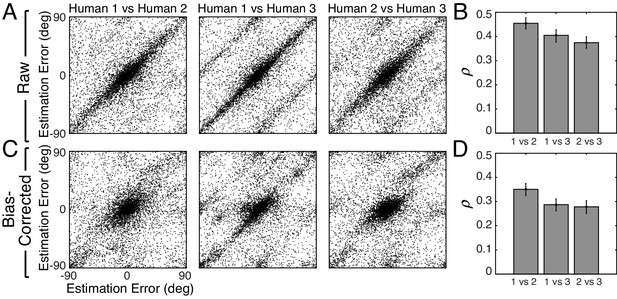
Trial-by-trial estimation errors between humans.
The diagonal structure in the plots indicates that trial-by-trial errors are correlated. (A) Raw trial-by-trial errors with natural stimuli between humans. (B) Correlation coefficients (circular) for trial-by-trial errors between humans. The error bars represent 95% confidence intervals from 1000 bootstrapped samples of the correlation coefficient. (C) Bias-corrected errors in natural stimuli. (D) Correlation coefficient for bias-corrected errors.
Figure 6—figure supplement 2
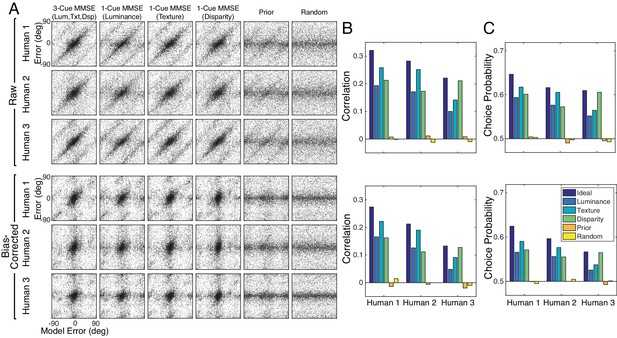
Six alternative models for predicting human tilt estimation performance.
Each model sets its estimates equal to (i) the minimum mean squared error (MMSE) estimates based on three cues (i.e., the normative model used in the main text); (ii–iv) the MMSE estimates based on each single cue alone (Luminance; Texture; and Disparity); (v) random tilt samples from the tilt prior (Prior); and (vi) random tilt samples from a uniform distribution of tilts (Random) (A) Human trial-by-trial errors plotted against the errors made by each of the models. Upper rows show raw errors; lower rows show bias-corrected errors. (B) Circular correlation coefficient for each of the models considered in (A). (C) Choice probability for each of the models considered in (A). Here, we define choice probability as the proportion of trials in which the sign of the model error predicts the sign of the human errors. The pattern is similar to that of the circular correlation coefficient. The MMSE model based on three image cues predicts humans tilt estimation errors better than all other models. In addition to the six models shown here, we assessed a number of ad hoc models. Three single-cue models that set the tilt estimate equal to each of the single cue values (i.e., cue-gradient orientation) predict human performance more poorly than the three-cue normative model used in the main text, but better than the prior or the random model. A model that averages the single-cue values (with equal weights) predicts human estimation better than the single-cue MMSE estimators, but worse than the three-cue normative model used in the main text.
Figure 7
The effect of slant and distance on tilt estimation error in natural stimuli for human and model observers.
(A) Absolute error decreases linearly with slant. Estimation error decreases approximately 20° as slant changes from 30° to 60°. (B) Absolute error increases linearly with distance. Estimation error increases approximately 15° as distance increases from 3 m to 30 m.
Figure 8 with 1 supplement
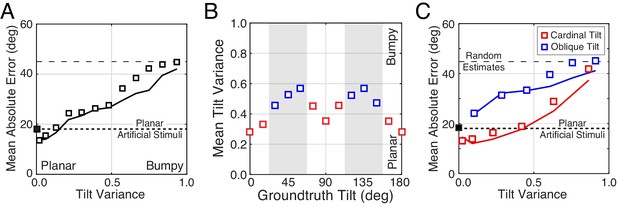
The effect of tilt variance on tilt estimation error.
(A) Absolute error increases linearly with tilt variance. Estimation error increases approximately 25° across the range of tilt variance. Artificial stimuli were perfectly planar and had zero local depth variation; hence the individual data point at zero tilt variance. Solid curve shows the model prediction. (B) Tilt variance co-varies with groundtruth tilt. Oblique tilts tend to be associated with less planar (i.e., more bumpy) regions of natural scenes. (Tilt variance was computed in 15° wide bins.) (C) Same as (A) but conditional on whether groundtruth tilts are cardinal (red, 0° ± 22.5° or 90° ± 22.5°) or oblique (blue, 45° ± 22.5° or 135° ± 22.5°, shaded areas in [B]). Data points are spaced unevenly because they are grouped in quantile bins, such that each data point represents an equal number of stimuli. The solid curves represent the errors of the MMSE estimator for cardinal (red) and oblique (blue) groundtruth tilts. The normative model predicts performance in all cases.
Figure 8—figure supplement 1
Tilt estimation performance with near-planar natural stimuli .
We analyzed performance for the subset of natural stimuli with the lowest tilt variance (tilt variance0.2; bottom 25%). For these near-planar stimuli, the mean tilt estimation error is 16.9°, slightly lower than the mean error with artificial stimuli (18.1°; see Figure 7C). (A) Raw responses. (B) Histogram of estimates. The dashed curve shows the distribution of groundtruth tilts in this subset of stimuli, which is not uniform. Unlike with planar artificial stimuli (c.f., Figure 2D), the histogram of human responses to near-planar natural stimuli over-represents the cardinal tilts relative to the frequency of the presented stimuli. The normative model nicely predicts the histogram of human estimates (solid curve). (C) Mean estimates as a function of groundtruth tilt. (D) Estimate variance as a function of groundtruth tilt. The mean and variance functions are different from the mean and variance functions yielded by planar artificial stimuli. Thus, tilt variance is not solely responsible for the differences between performance with natural and artificial stimuli. (E) Tilt estimation errors for different groundtruth tilts. Errors with near-planar natural stimuli (gray symbols) are substantially different than estimation errors with planar artificial stimuli (black symbols). The error distributions shown here are noisier than the plots in Figure 3, because there are comparatively fewer stimuli with low tilt variance. Still, the model (gray curves) does a reasonable job at predicting the distributions. Indeed, for near-planar natural stimuli, all three humans observers show significant trial-by-trial raw error correlations with the model, and two of three observers show significant trial-by-trial bias-corrected error correlations with the model.
Figure 9 with 1 supplement
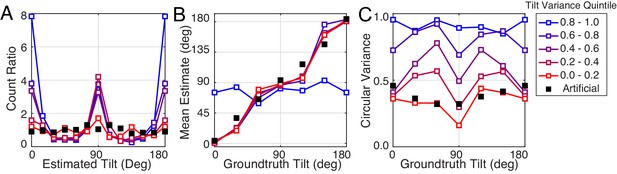
Robustness of performance measures to tilt variance.
Human tilt estimation performance with natural stimuli for five tilt variance quintiles (colors). The quintile centers are at 0.12, 0.33, 0.55, 0.76, and 0.97, respectively. (A) Estimate count ratio (i.e., the ratio of estimated to presented tilt) at each tilt. With near-planar natural stimuli, cardinal tilts are still estimated much more frequently than with planar artificial stimuli. (B) Estimate means. (C) The variance of estimates. Except with the highest tilt variance stimuli, the patterns of mean and variance with natural stimuli hold across tilt variances, except for natural stimuli with the highest tilt variance.
Figure 9—figure supplement 1
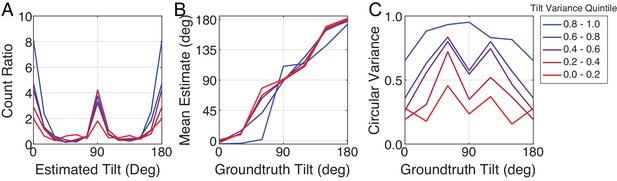
Tilt estimation performance of the normative model with natural stimuli for five tilt variance quintiles.
The quintile centers are at 0.12, 0.33, 0.55, 0.76, and 0.97, respectively. (A) Estimate count ratio (i.e., the ratio of estimated to presented tilts) at each tilt. (B) Estimate means. (C) Estimate variances. The patterns of estimate counts, estimate means, and estimates variances are robust to tilt variance except at the very highest tilt variances.
Author response image 1
Model performance on artificial stimuli
https://doi.org/10.7554/eLife.31448.028Additional files
-
Source data 1
Source data for full-field natural scene experiment.
- https://doi.org/10.7554/eLife.31448.023
-
Source data 2
Source data for human performance.
- https://doi.org/10.7554/eLife.31448.024
-
Source data 3
Source data for MMSE model.
- https://doi.org/10.7554/eLife.31448.025
-
Transparent reporting form
- https://doi.org/10.7554/eLife.31448.026
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The lawful imprecision of human surface tilt estimation in natural scenes
eLife 7:e31448.
https://doi.org/10.7554/eLife.31448
