Striatal action-value neurons reconsidered
- The Hebrew University of Jerusalem, Israel
Figures
Figure 1
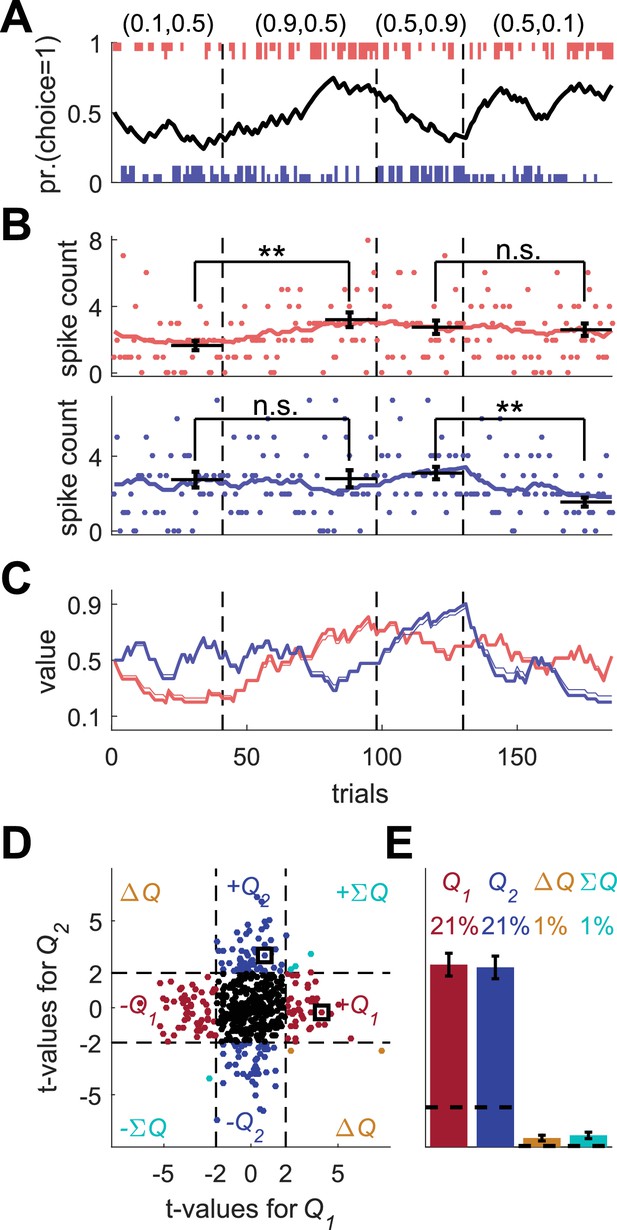
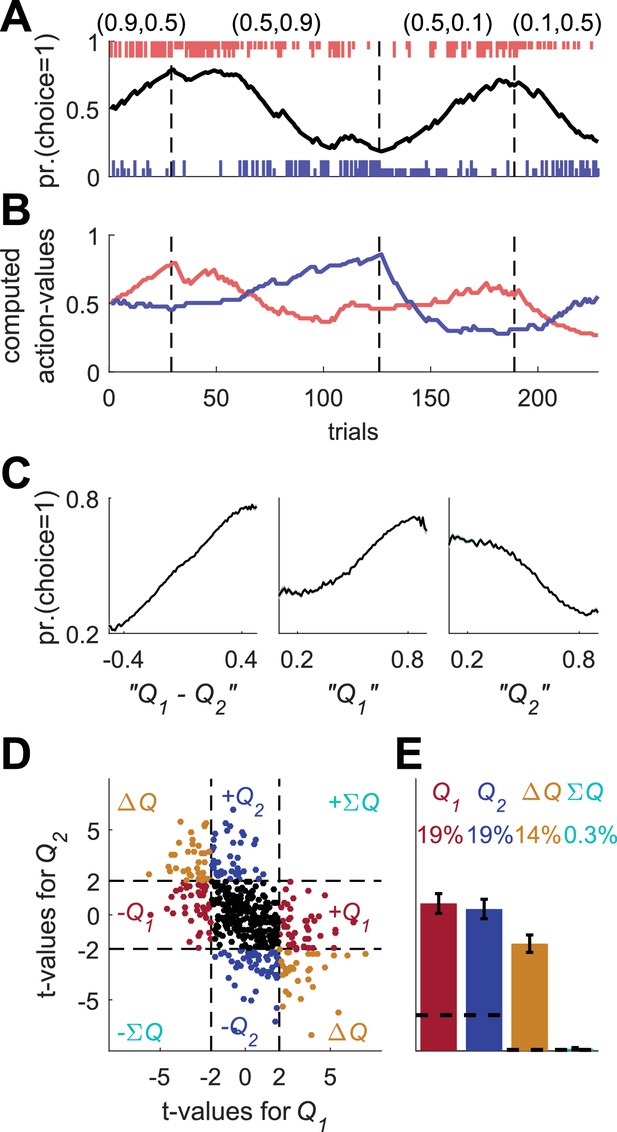
Model of action-value neurons.
(A) Behavior of the model in an example session, composed of four blocks (separated by dashed vertical lines). The probabilities of reward for choosing actions 1 and 2 are denoted by the pair of numbers above the block. Black line denotes the probability of choosing action 1; vertical lines denote choices in individual trials, where red and blue denote actions 1 and 2, respectively, and long and short lines denote rewarded and unrewarded trials, respectively. (B) Neural activity. Firing rate (line) and spike-count (dots) of two example simulated action-value neurons in the session depicted in (A). The red and blue-labeled neurons represent and , respectively. Black horizontal lines denote the mean spike count in the last 20 trials of the block. Error bars denote the standard error of the mean. The two asterisks denote p<0.01 (rank sum test). (C) Values. Thick red and blue lines denote and , respectively. Note that the firing rates of the two neurons in (B) are a linear function of these values. Thin red and blue lines denote the estimates of and , respectively, based on the choices and rewards in (A). The similarity between the thick and thin lines indicates that the parameters of the model can be accurately estimated from the behavior (see also Materials and methods). (D) and (E) Population analysis. (D) Example of 500 simulated action-value neurons from randomly chosen sessions. Each dot corresponds to a single neuron and the coordinates correspond to the t-values of the regression of the spike counts on the estimated values of the two actions. Dashed lines at t=2 denote the significance boundaries. Color of dots denote significance: dark red and blue denote a significant regression coefficient on exactly one estimated action-value, action 1 or action 2, respectively; light blue – significant regression coefficients on both estimated action-values with similar signs (); orange - significant regression coefficients on both estimated action-values with opposite signs (); Black – no significant regression coefficients. The two simulated neurons in (B) are denoted by squares. (E) Fraction of neurons in each category, estimated from 20,000 simulated neurons in 1,000 sessions. Error bars denote the standard error of the mean. Dashed lines denote the naïve expected false positive rate from the significance threshold (see Materials and methods).
Figure 2 with 10 supplements
Erroneous detection of action-value representation in random-walk neurons.
(A) Two example random-walk neurons that appear as if they represent action-values. The red (top) and blue (bottom) lines denote the estimated action-values 1 and 2, respectively that were depicted in Figure 1C. Gray lines and gray dots denote the firing rates and the spike counts of two example random-walk neurons that were randomly assigned to this simulated session. Black horizontal lines denote the mean spike count in the last 20 trials of each block. Error bars denote the standard error of the mean. The two asterisks denote p<0.01 (rank sum test). (B) and (C) Population analysis. Each random-walk neuron was regressed on the two estimated action-values, as in Figure 1D and E. Numbers and legend are the same as in Figure 1D and E. The two random-walk neurons in (A) are denoted by squares in (B). Dashed lines in (B) at t=2 denote the significance boundaries. Dashed lines in (C) denote the naïve expected false positive rate from the significance threshold (see Materials and methods). (D) Fraction of random-walk neurons classified as action-value neurons (red), and classified as state neurons () or policy neurons () (green) as a function of the magnitude of the diffusion parameter of random-walk (). Light red and light green are standard error of the mean. Dashed lines denote the results for =0.1, which is the value of the diffusion parameter used in (A)-(C). Initial firing rate for all neurons in the simulations is Hz.
Figure 2—figure supplement 1
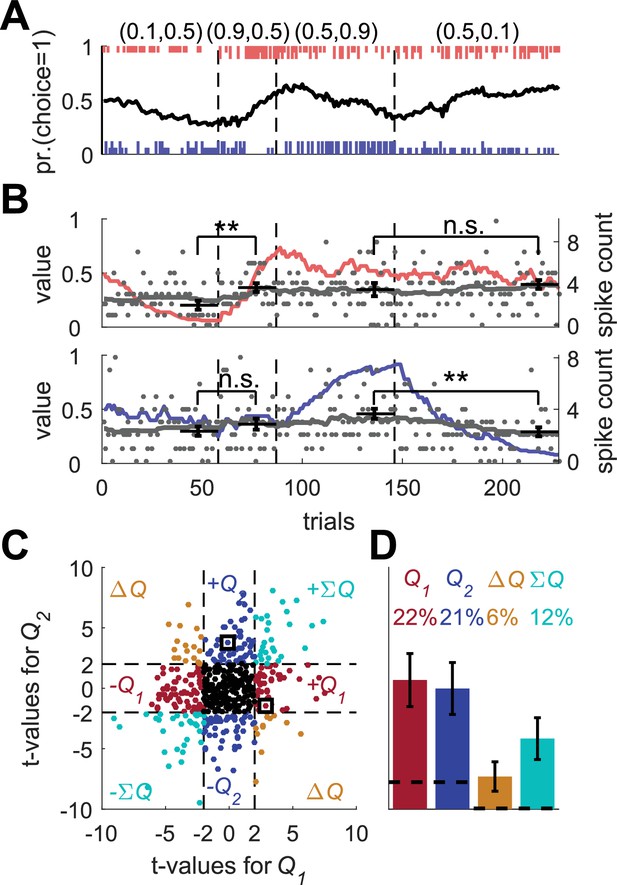
Erroneous detection of action-value representation in a model with covariance based synaptic plasticity.
(A) An example of operant learning by the covariance model (see Materials and methods). Legend is the same as in Figure 1A. (B) Two example covariance neurons that appear is if they represent action-values. The red (top) and blue (bottom) lines denote the calculated action-values 1 and 2, respectively, that were computed from the behavior of the model. Gray lines and gray dots denote the firing rates and the spike counts of two example covariance neurons. Black horizontal lines denote the mean spike count in the last 20 trials of each block. Error bars denote the standard error of the mean. The two asterisks denote p<0.01 (rank sum test). Legend is the same as in Figure 2A. (C) and (D) Population analysis. Same as in Figure 1D and E. Each simulated neuron was regressed on the computed action-values. The two simulated neurons in (B) are denoted by squares in (C). Results in (D) are based on 500 sessions with 2000 simulated neurons in a session. Legend is the same as in Figure 1D and E. Dashed lines in (C) at t = 2 denote the significance boundaries. Dashed lines in (D) denote the naïve expected false positive rate from the significance threshold (see Materials and methods). Error bars denote the standard error of the mean. Following this standard approach, 43% of the covariance neurons were erroneously classified as representing action-values.
Figure 2—figure supplement 2
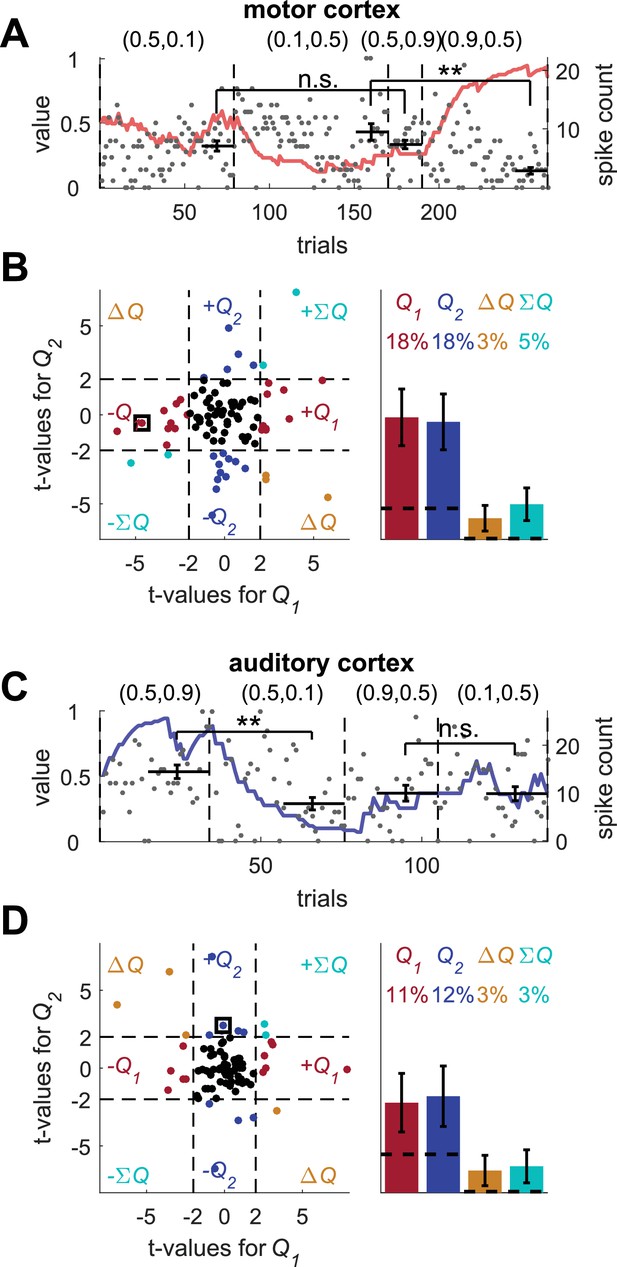
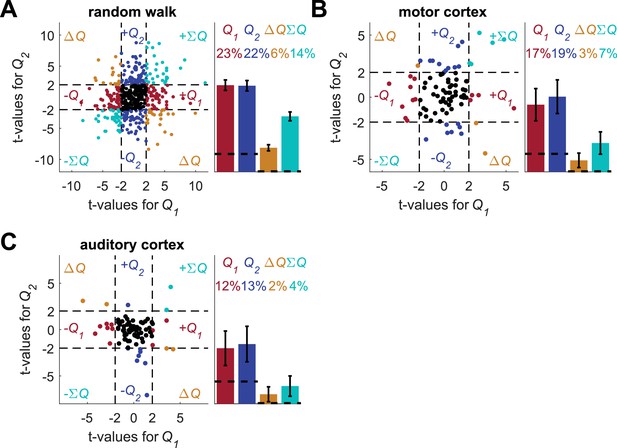
Erroneous detection of action-value neurons in unrelated experiments.
(A) and (B) motor cortex neurons (A) An example motor cortex neuron recorded in a BMI task, presented as if the sequence of spike counts of this neuron corresponds to the sequence of trials in a randomly chosen session of operant learning from the sessions used for the population analysis in Figure 1E. Gray dots denote the spike-counts. Black horizontal line denotes the mean spike counts in the last 20 trials of the assigned blocks. Error bars denote the standard error of the mean. The two asterisks denote p<0.01 (rank sum test). For each neuron, we computed the t-values of the regression of the spike count on the two corresponding estimated action-values. The red line denotes the action-value whose t-value exceeded 2 (in absolute value). (B) Population analysis. Left scatter plot, the t-values of 89 neurons regressed on the estimated action-values of 89 randomly selected sessions (same as Figure 1D). The neuron in (A) is denoted by a square. Dashed lines at t = 2 denote the significance boundaries. Right bar chart, fraction of neurons classified in each category, estimated by regressing each of the 89 motor cortex neurons on 80 different estimated action-values from 40 randomly selected sessions. Dashed lines denote the naïve expected false positive rate from the significance threshold (see Materials and methods). Error bars denote the standard error of the mean. Legend is the same as in Figure 1D and E. (C) and (D) auditory cortex neurons from (Hershenhoren et al., 2014). (C) Same as in (A) for an auditory cortex neuron in an anesthetized rat responding to the presentation of pure tones. (D) Population analysis. Left scatter plot, the t-values of 82 recorded sessions from auditory neurons regressed on the estimated action-values of 82 randomly selected sessions (same as (B)). The neuron in (C) is denoted by a square. Right bar chart, fraction of neurons classified in each category, estimated by regressing 125 recorded sessions from auditory cortex neurons on 80 different estimated action-values from 40 randomly selected sessions (in each session, 34% of recordings were excluded on average, see Materials and methods). Error bars denote the standard error of the mean. Following this standard approach, 36% of the motor cortex neurons and 23% of the auditory cortex neurons were erroneously classified as representing action-values. These results demonstrate that the magnitude of non-stationarity in standard electrophysiological recordings is sufficient to result in an erroneous identification of neurons as representing action-values.
Figure 2—figure supplement 3
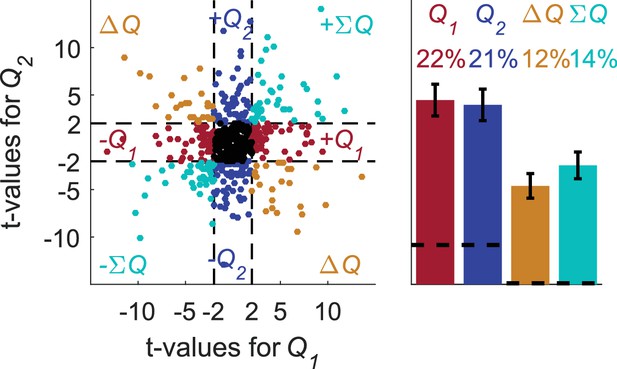
Erroneous detection of unrelated action-value representations in basal ganglia neurons.
Population analysis on basal ganglia neurons. Spike counts were regressed on estimated action-values that were created in the same experimental setting as in Figure 1. To compare with the number of blocks and trials used in the original analysis, we simulated sessions with more blocks, so that the original four blocks were repeated in random permutation, and with a weaker bias towards the higher-valued action (). The average number of blocks and trials used in this analysis is 6 and 516.5, respectively. Left scatter plot, the t-values of the 214 neurons from (Ito and Doya, 2009) in three different phases regressed on the estimated action-values from 642 randomly selected simulated sessions (same analysis as in Figure 2—figure supplement 2B,D). Dashed lines at t = 2 denote the significance boundaries. Right bar chart, fraction of neurons classified in each category, estimated by regressing the 214 neurons in three different phases on 80 different estimated action-values from 40 randomly selected sessions (see Materials and methods). Dashed lines denote the naïve expected false positive rate from the significance threshold (see Materials and methods). Error bars denote the standard error of the mean. Legend is the same as in Figure 1D and E. This analysis erroneously classified 43% of the neurons as action-value neurons, despite the fact that these action-values were completely unrelated to the experimental session in which these neurons were recorded.
Figure 2—figure supplement 4
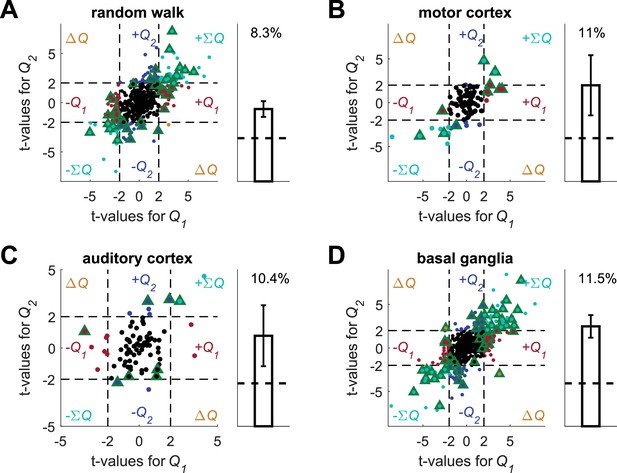
Spike count permutation (as in [Kim et al., 2009]) does not resolve the temporal correlations confound.
Conducting this analysis using the four data sets and unrelated, simulated action-values we erroneously detect action-value representation in all data sets. (A) (B) (C) and (D) denote the random-walk neurons, motor cortex neurons, auditory cortex neurons and basal ganglia neurons, respectively. Left, t-values from regressions of the original spike-count on the estimated action-values. Green triangles denote significant modulation by action-value according to the permuted spike-count analysis (see Materials and methods). Legend otherwise is the same as in Figure 1D. Dashed black lines at t=2 denote the significance boundaries that would be used in the standard analysis. Right, fraction of neurons significantly modulated by action-value according to the permuted spike-count analysis across the population (0.05, expected by chance, is denoted by a horizontal dashed line). Error bars are standard error of the mean. Number of neurons used in (A) (B) (C) and (D) is the same as in Figure 2, Figure 2—figure supplement 2A–B, Figure 2—figure supplement 2C–D and Figure 2—figure supplement 3, respectively. Note that in all four cases the two t-values are correlated. This results from the correlation between and caused by the reward schedule in (Kim et al., 2009).
Figure 2—figure supplement 5
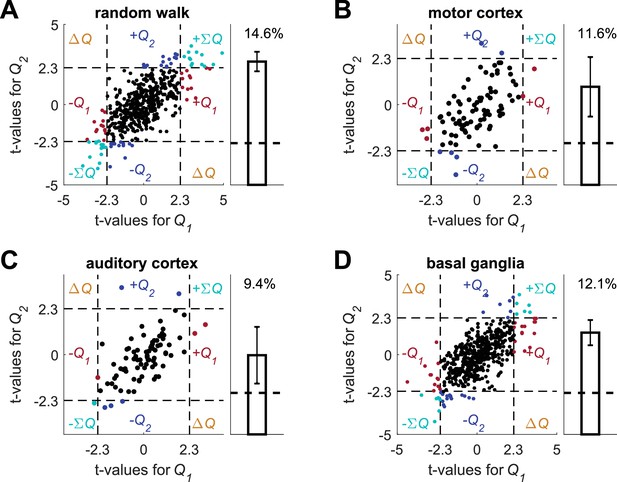
Autoregressive coefficients do not resolve the temporal correlations confound.
Following (Kim et al., 2013), we simulated the experimental settings in (Kim et al., 2013) to create simulated action-values (see also Meterials and methods on Figure 2—figure supplement 4, with the same experimental design, but with a different statistical analysis) and conducted a multiple linear regression analysis on each of the unrelated data sets, using the simulated action-values and the following regression model: where is the spike count in trial , and are the estimated action-values in trial , is the action chosen in trial , is the reward in trial , is the interaction between choice and reward in trial , where both are expressed as binary with values {-1,1}, is the value of the action that was chosen on trial , are the spike counts one, two and three trials prior to the current trial, is the residual error in trial and are the regression parameters. (A) (B) (C) and (D) denote the random-walk neurons, motor cortex neurons, auditory cortex neurons and basal ganglia neurons, respectively. Left, t-values from the regression of the spike-counts on and in the regression model. The significance boundaries for the t-values, denoted by dashed lines, are 2.3, corresponding to p<0.025. Right, fraction of neurons significantly modulated by action-value across the population (0.05, expected by chance, is denoted by a horizontal dashed line). Error bars are standard error of the mean. Number of neurons used in (A) (B) (C) and (D) is the same as in Figure 2, Figure 2—figure supplement 2A–B, Figure 2—figure supplement 2C–D and Figure 2—figure supplement 3, respectively. Legend is the same as in Figure 1D. Note that in all four cases the two t-values are correlated. This results from the correlation between and caused by the reward schedule in (Kim et al., 2013).
Figure 2—figure supplement 6
Regression on reward probabilities does not resolve the temporal correlations confound.
Following (Ito and Doya, 2009; Samejima et al., 2005) for each of the four data-sets (A) random-walk (B) motor cortex (C) auditory cortex and (D) basal ganglia neurons, spike counts in the last 20 trials in each block (from randomly assigned simulated experimental settings, the assignment was the same as in the standard analysis in Figure 2, Figure 2—figure supplement 2A–B, Figure 2—figure supplement 2C–D and Figure 2—figure supplement 3 ) were regressed on reward probabilities (e.g., (0.5,0.9)) in those blocks. This is similar to the analysis in the individual examples of Figures 1B and 2A, Figure 2—figure supplement 1B, Figure 2—figure supplement 2A, and Figure 2—figure supplement 2C (in which two rank sum tests, and not regression, were used). Left of each panel denotes the t-values of the regressions of individual neurons (Dashed lines at t = 2 denote the significance boundaries) and right bar graphs denote the population statistics (Dashed lines denote the naïve expected false positive rate from the significance threshold, see Materials and methods). Number of neurons used in (A) (B) (C) and (D) is the same as in Figure 2, Figure 2—figure supplement 2A–B, Figure 2—figure supplement 2C–D and Figure 2—figure supplement 3, respectively. Legend is the same as in Figure 1D and E. Note that for this analysis we considered significance using the threshold of p<0.05. By contrast, in (Ito and Doya, 2009) the same analysis was used with a significance threshold of p<0.01. For comparison, when considering the basal ganglia neurons with a significance threshold of p<0.01, the number of neurons that are erroneously classified as action-value neurons decreases from 37 ± 3.3% to 26 ± 3%.
Figure 2—figure supplement 7
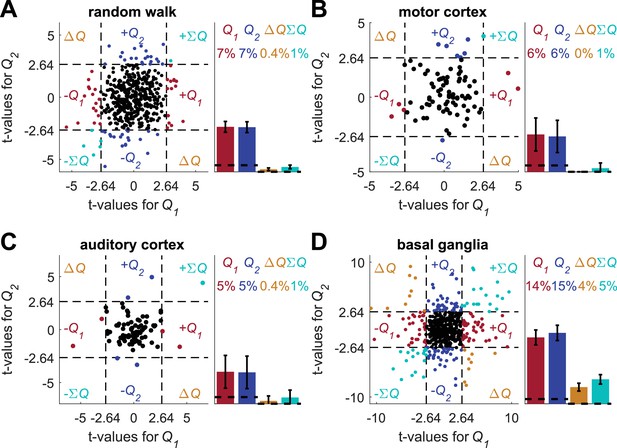
Detrending analysis does not resolve the temporal correlations confound.
Following (Ito and Doya, 2015a), we conducted a multiple linear regression analysis using unrelated action-values (the same action-values as in Figure 2—figure supplement 6) and the following regression model:
Where is the spike count in trial , and are the estimated action-values in trial , and are the actions chosen in trial and , respectively, and are the rewards in trial and , respectively, is the residual error in trial and are the regression parameters. (A) (B) (C) and (D) denote the random-walk neurons, motor cortex neurons, auditory cortex neurons and basal ganglia neurons, respectively. Left, t-values from regressions of the spike-counts on and in the regression model. As in (Ito and Doya, 2015a), the significance boundaries for the t-values, denoted by dashed black lines, are 2.64, corresponding to p<0.01 (as opposed to p<0.05 elsewhere). Right bar graphs denote the population statistics. Dashed lines denote the naïve expected false positive rate from the significance threshold (see Materials and methods). Note, however, that the significance criterion is more stringent and the expected total number of identified action-value neurons by chance is only 2%. Number of neurons used in (A) (B) (C) and (D) is the same as in Figure 2, Figure 2—figure supplement 2A–B, Figure 2—figure supplement 2C–D and Figure 2—figure supplement 3, respectively. Legend is the same as in Figure 1D and E.
Figure 2—figure supplement 8
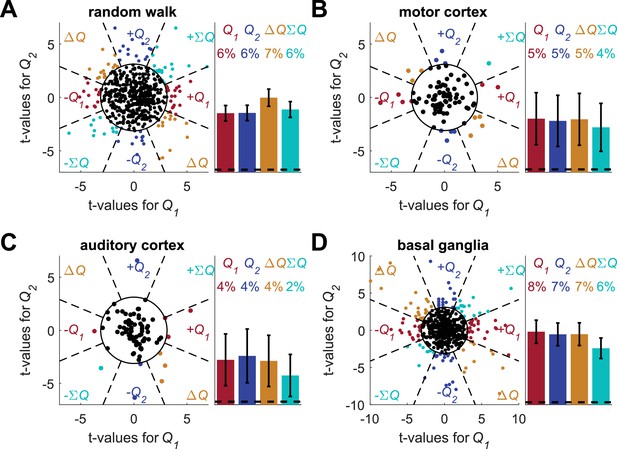
Unbiased classification of action-value neurons does not resolve the temporal correlations confound.
Following (Wang et al., 2013) (whose main focus was state-value representation), we considered an unbiased classification of action-value neurons. (A) (B) (C) and (D) denote the random-walk neurons, motor cortex neurons, auditory cortex neurons and basal ganglia neurons, respectively. The t-values for the different neurons are identical to Figure 2—figure supplement 6 (and unlike (Wang et al., 2013) this analysis used only the last 20 trials in each block). The f-value of each neuron was computed from the regression and a neuron was considered as non-significant (black dot) if p>0.01, denoted by the circle in the left panels. For the significant neurons, the dashed lines define eight equal-angle sectors, each corresponding to a different classification of the neuron. Right is the population analysis. Dashed lines denote the naïve expected false positive rate from the significance threshold (see Materials and methods). Note that the expected total number of identified significant neurons by chance is only 1%. Number of neurons used in (A) (B) (C) and (D) is the same as in Figure 2, Figure 2—figure supplement 2A–B, Figure 2—figure supplement 2C–D and Figure 2—figure supplement 3, respectively. Legend is the same as in Figure 1D and E.
Figure 2—figure supplement 9
Random intermingling of estimated action-values does not resolve the temporal correlations confound.
In the spirit of the experiment conducted by (FitzGerald et al., 2012) we simulated an experiment, in which two different trial types are marked by cues, randomly selected every trial, and action-values are learned separately for each cue. Specifically, each session in this new design was created by a random intermingling of two different, randomly-selected sessions from those analyzed in Figure 1. The number of trials in the intermingled session was equal to the number of trials in one of the two randomly-selected original sessions. As a result, we only used approximately the first half of each of the original sessions. We created 1000 such intermingled sessions. Next, we regressed the spike counts of neurons from each of the four data-sets (A) random-walk neurons, (B) motor cortex neurons (C) auditory cortex neurons and (D) basal ganglia neurons on the resulting intermingled estimated action-values. Left of each panel denotes the t-values of the regressions of individual neurons (Dashed lines at t = 2 denote the significance boundaries) and right bar graphs denote the population statistics (Dashed lines denote the naïve expected false positive rate from the significance threshold, see Materials and methods). Number of neurons used in (A) (B) (C) and (D) is the same as in Figure 2, Figure 2—figure supplement 2A–B, Figure 2—figure supplement 2C–D and Figure 2—figure supplement 3, respectively. Legend is the same as in Figure 1D and E. These results show that even when using a design where trials are chosen randomly, there can still be temporal correlations in the predictors of the model. In this case, this occurs because the temporal correlations in each estimated action-value still create temporal correlations in the intermingled vector.
Figure 2—figure supplement 10
Increasing the number of blocks does not resolve the temporal correlations confound.
We repeated the standard analysis with eight blocks, so that the four blocks from the experiment in Figure 1A were repeated twice, each time in random permutation. The mean length of the sessions was 347 trials (standard deviation 65 trials). For each of the three data-sets (A) random-walk neurons, (B) motor cortex neurons and (C) auditory cortex neurons, the spike-counts were regressed on the longer estimated action-values from the 8-block sessions (for auditory cortex analysis only 676 sessions with 370 or fewer trials were used). Left of each panel denotes the t-values of the regressions of individual neurons (Dashed lines at t = 2 denote the significance boundaries) and right bar graphs denote the population statistics (Dashed lines denote the naïve expected false positive rate from the significance threshold, see Materials and methods). Number of neurons used in (A), (B) and (C) is the same as in Figure 2, Figure 2—figure supplement 2A–B and Figure 2—figure supplement 2C–D, respectively. Legend is the same as in Figure 1D and E. We did not perform this analysis on the basal ganglia neurons because we already used longer sessions in the original analysis for these recordings (see Figure 2—figure supplement 3).
Figure 3 with 1 supplement
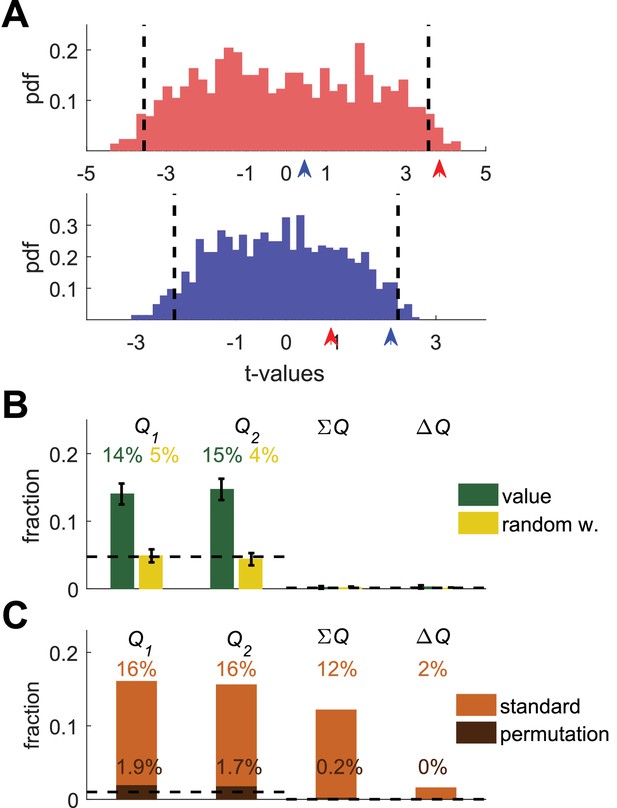
Permutation analysis.
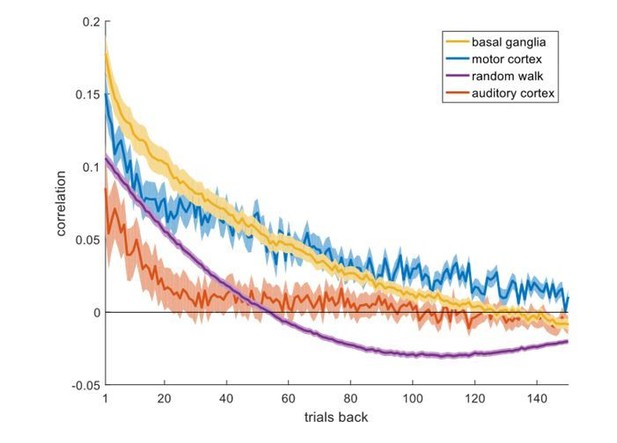
(A) Red and blue correspond to red and blue - labeled neurons in Figure 1B. Arrow-heads denote the t-values from the regressions on the estimated action-values from the session in which the neuron was simulated (depicted in Figure 1A). The red and blue histograms denote the t-values of the regressions of the spike-count on estimated action-values from different sessions in Figure 1E (Materials and methods). Dashed black lines denote the 5% significance boundary. In this analysis, the regression coefficient of neural activity on an action-value is significant if it exceeds these significance boundaries. Note that because of the temporal correlations, these significance boundaries are larger than ±2 (the significance boundaries in Figure 1,2). According to this permutation test the red-labeled but not the blue-labeled neuron is classified as an action-value neuron (B) Fraction of neurons classified in each category using the permutation analysis for the action-value neurons (green, Figure 1) and random-walk neurons (yellow, Figure 2).Dashed lines denote the naïve expected false positive rate from the significance threshold (Materials and methods). Error bars denote the standard error of the mean. The test correctly identifies 29% of actual action-value neurons as such, while classification of random-walk neurons was at chance level. Analysis was done on 10,080 action-value neurons and 10,077 random-walk neurons from 504 simulated sessions (C) Light orange, fraction of basal ganglia neurons from (Ito and Doya, 2009) classified in each category when regressing the spike count of 214 basal ganglia neurons in three different experimental phases on the estimated action-values associated with their experimental session. This analysis classified 32% of neurons as representing action-values. Dark orange, fraction of basal ganglia neurons classified in each category when applying the permutation analysis. This test classified 3.6% of neurons as representing action-value. Dashed line denotes significance level of p<0.01.
Figure 3—figure supplement 1
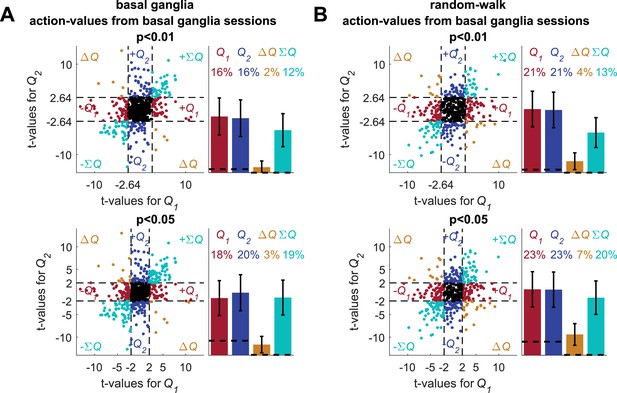
Analyses of basal ganglia data using estimated action-values from the neurons' sessions.
(A) The standard analysis on the neuronal recordings taken from (Ito and Doya, 2009), using action-values estimated from the behavior in the sessions in which the neurons were recorded. The top and bottom scatter plots are identical, except for the significance boundries. They depict the t-values from the results of the regression of 640 of 642 neuronal recordings (214 neurons 3 phases) on the action-values that were estimated from the original experiment (see Materials and methods for estimation of action-values). Legend is the same as in Figure 1D and E (Dashed lines in the right panels at t=2, 2.64 denote the significance boundaries and the dashed lines on the left panels denote the naïve expected false positive rate from the significance threshold, see Materials and methods). This analysis is different from the one used in (Ito and Doya, 2009), which was similar to the one described in (Figure 2—figure supplement 6). Two neurons do not appear on the scatter plots, whose axes were bounded for ease of viewing. Their t-values were (2.44, 18.91) and (1.08, 16.96) for action-value 1 and 2, respectively. (B) For comparsion, we repeated the analysis using the random-walk neurons (Figure 2). The fraction of erroenusly classified action-value neurons is comparable to that extracted from the experimental data. Remarkably, bias in favor of 'state'-representing neurons over 'policy'-representing neurons observed in the recorded neurons is also present in the random-walk neurons. This suggests that the overrepresentation of state neurons is not necessarily of biological significance.
Figure 4
A possible solution for the temporal correlations confound that is based on a trial design.
(A) A Q-learning model was simulated in 1,000 sessions of 400 trials, where the original reward probabilities (same as in Figure 1A) were associated with different cues and appeared randomly. Learning was done separately for each cue. Top panel: The first 20 trials in an example session. Background colors denote the reward probabilities in each trial. Black circles denote the learned value of action-value 1 in each trial. Top and bottom black lines denote choices of action 1 and 2, respectively. Long and short lines denote rewarded and unrewarded trials, respectively. Bottom panels: Two examples of the grouping of trials with the same reward probabilities to show the continuity in learning. Note that the action-value changes only when action 1 is chosen because it is the action-value associated with action 1. (B) and (C) population analysis for action-value neurons. 20,000 action-value neurons were simulated from the model in (A), similarly to the action-value neurons in Figure 1. For each neuron, the spike-counts in the last 200 trials of the session were regressed on the reward probabilities (see Materials and methods). Legend is the same as in Figure 1D–E. Dashed lines in (B) at t=2 denote the significance boundaries. Dashed lines in (C) denote the naïve expected false positive rate from the significance threshold (see Materials and methods). This analysis correctly identifies 59% of action-value neurons as such. (D) and (E) population analysis for random-walk neurons. 20,000 Random-walk neurons were simulated as in Figure 2. Same regression analysis as in (B) and (C). Only 8.5% of the random-walk neurons were erroneously classified as representing action-values (9.5% chance level).
Figure 5 with 1 supplement
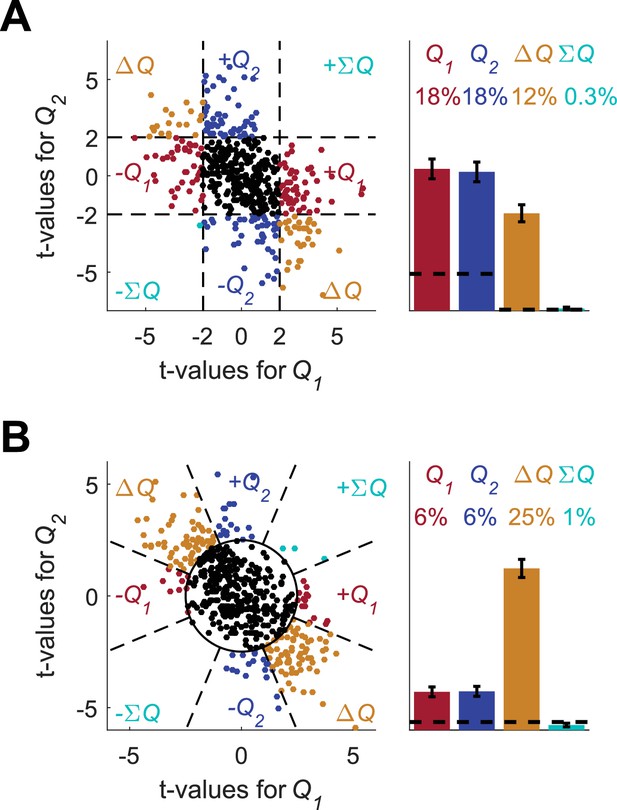
Erroneous detection of action-value representation in policy neurons.
(A) Behavior of the model in an example session, same as in Figure 1A for the direct-policy model. (B) Red and blue lines denote ‘action-values’ 1 and 2, respectively, calculated from the choices and rewards in (A). Note that the model learned without any explicit or implicit calculation of action-values. The extraction of action-values in (B) is based on the fitting of Equation 1 to the learning behavior. (C) Strong correlation between policy from the direct-policy algorithm and action-values extracted by fitting Equation 1 to behavior. The three panels depict probability of choice as a function of the difference between the calculated action-values (left), ‘’ (center) and ‘’ (right). This correlation can cause policy neurons to be erroneously classified as representing action-values (D) and (E) Population analysis, same as in Figure 1D and E for the policy neurons. Legend and number of neurons are also as in Figure 1D and E. Dashed lines in (D) at t=2 denote the significance boundaries. Dashed lines in (E) denote the naïve expected false positive rate from the significance threshold (see Materials and methods).
Figure 5—figure supplement 1
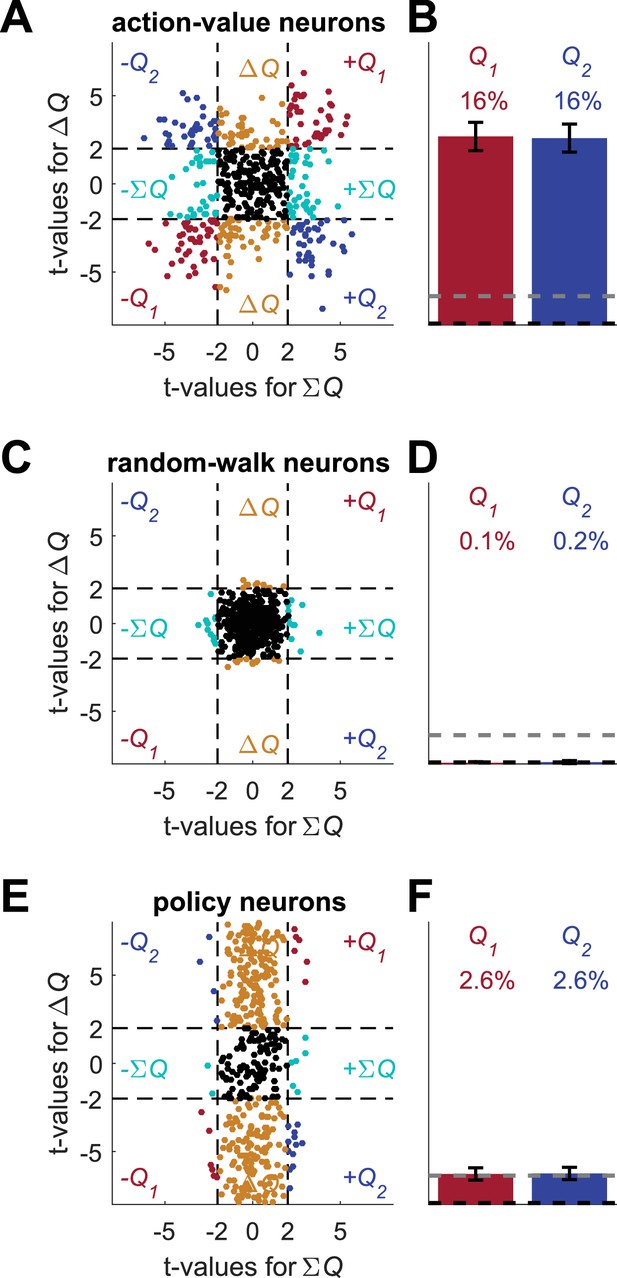
Alternative analyses do not resolve the correlated decision variables confound.
(A) Regression analysis on policy neurons with choice as an added regressor. Following common experimental practice, we used the following regression model: where is the spike count in trial , and are the estimated action-values in trial , is a binary variable indicating whether action 1 was chosen, is the residual error in trial and are the regression parameters. Simulated neurons are the same as in Figure 5E. Legend is the same as Figure 1D and E (Dashed lines in the right panels at t=2 denote the significance boundaries and the dashed lines on the left panels denote the naïve expected false positive rate from the significance threshold, see Materials and methods). (B) Unbiased analysis. Following (Wang et al., 2013), we considered an analysis in which the probability of erroneous classification for data that is not related to the task is equal between action-value 1, action-value 2, state and policy. The f-value of each neuron was computed from the regression on the two calculated action-values and a neuron was considered as non-significant (black dot) if p>0.05, denoted by the circle in the left figure. For the significant neurons, the dashed lines define 8 equal-angle sectors, each corresponding to a different classification of the neuron, similarly to Figure 2—figure supplement 8. The figure on the right is the population analysis (Dashed lines denote the naïve expected false positive rate from the significance threshold, see Materials and methods). Note that the fraction of neurons that is expected to be classified as action-value neurons by chance is only 2.5%. Simulated neurons are the same as in Figure 5E. Legend is the same as in Figure 1D and E. In the original paper, p<0.01 was used. For p<0.01 the analysis classifies 6% of neurons as action-value neurons (0.5% expected by chance) and 17% as neurons (0.25% expected by chance).
Figure 6
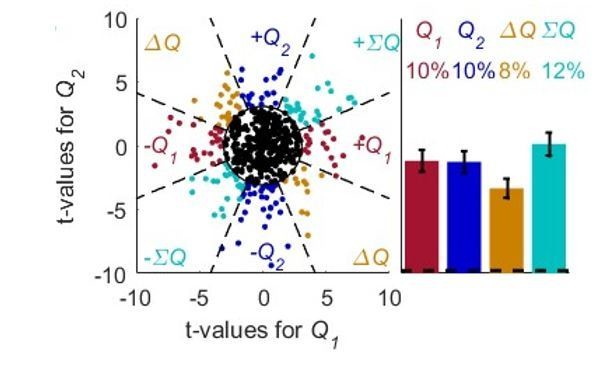
A possible solution for the policy and state confounds.
(A) The Q-learning model (Equations 1 and 2) was simulated in 1,000 sessions of 400 trials each, where the reward probabilities were associated with different cues and were randomly chosen in each trial, as in Figure 4. Learning occurred separately for each cue. In each session 20 action-value neurons, whose firing rate is proportional to the action-values (as in Figure 1) were simulated. For each neuron, the spike-counts in the last 200 trials of each session were regressed on the sum of the reward probabilities (; state) and the difference of the reward probabilities (; policy, see Materials and methods). Each dot denotes the t-values of the two regression coefficients of each of 500 example neurons. Dashed lines at t=2 denote the significance boundaries. Neurons that had significant regression coefficients on both policy and state were identified as action-value neurons. Colors as in Figure 1D. (B) Population analysis revealed that 32% of the action-value neurons were identified as such. Error bars are the standard error of the mean. Dashed black line denotes the expected false positive rate from randomly modulated neurons. Dashed gray line denotes the expected false positive rate from policy or state neurons (see Materials and methods) (C) Same as in (A) with random-walk neurons, numbers are as in Figure 2. (D) Population analysis revealed that less than 1% of the random-walk neurons were erroneously classified as representing action-values. (E-F) To test the policy neurons, we simulated a direct-policy learning algorithm (as in Figure 5) in the same sessions as in (A-D). Learning occurred separately for each cue. In each session 20 policy neurons, whose firing rate is proportional to the probability of choice (as in Figure 5) were simulated. As in (A-D), the spike-counts in the last 200 trials of each session were regressed on the sum and difference of the reward probabilities. (E) Each dot denotes the t-values of the two regression coefficients of each of 500 example neurons. (F) Population analysis. As expected, only 5% of the policy neurons were erroneously classified as representing action-values.
Author response image 1
Author response image 2
Author response image 3
Author response image 4
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.34248.020
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Striatal action-value neurons reconsidered
eLife 7:e34248.
https://doi.org/10.7554/eLife.34248
