A resource-rational theory of set size effects in human visual working memory
- University of Uppsala, Sweden
- New York University, United States
Figures
Figure 1
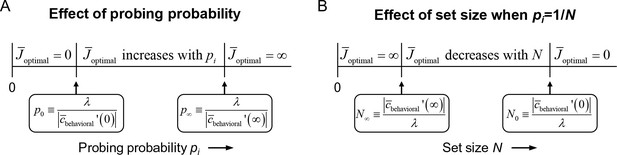
Effects of probing probability and set size on in the resource-rational model for local tasks.
(A) The model has three different optimal solutions depending on probing probability pi: invest no resource when pi is smaller than some threshold value p0, invest infinite resource when pi is larger than p∞, and invest a finite amount of resource when p0 <pi < p∞. The thresholds p0 and p∞ depend on weight λ (see Equation (1)) and on the derivative of the local expected behavioral cost function evaluated at 0 and ∞, respectively. If p0 >1, then only the first regime exists; if p0 <1 < p∞ then only the first two regimes exist. (B) If, in addition, pi = 1/N, then the domain of N partitions in a similar manner.
Figure 2 with 1 supplement
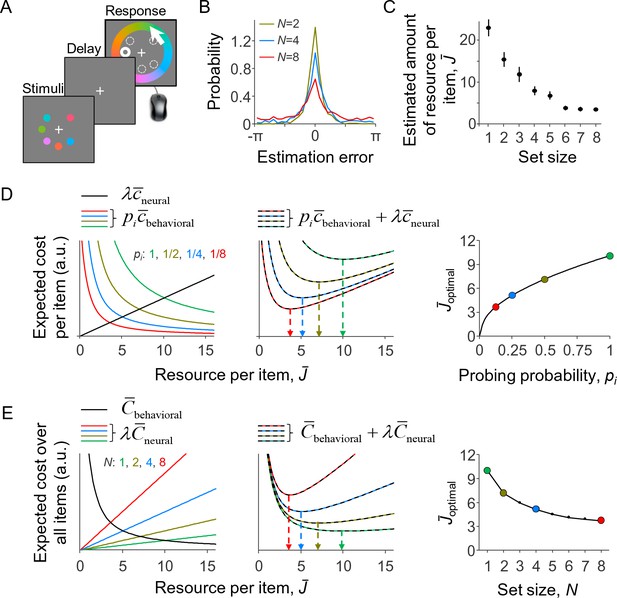
A resource-rational model for delayed-estimation tasks.
(A) Example of a trial in a delayed-estimation experiment. The subject is briefly presented with a set of stimuli and, after a short delay, reports the value of the item at a randomly chosen location (here indicated with thick circle). (B) The distribution of estimation errors in delayed-estimation experiments typically widens with set size (data from Experiment E5 in Table 1). (C) This suggests that the amount of resource per encoded item decreases with set size. The estimated amount of resource per item was computed using the same non-parametric model as the one underlying Figure 3C. (D) Expected cost per item as a function of the amount of invested resource (model parameters: λ = 0.01, β = 2, τ↓0). Left: The expected behavioral cost per item (colored curves) decreases with the amount of invested resource, while the expected neural cost per item increases (black line). Center: The sum of these two costs has a unique minimum, whose location (arrows) depends on probing probability pi. Right: The optimal amount of resource per item increases with the probability that the item will be probed. (E) Expected cost across all items, when each item is probed with a probability pi = 1/N; the model parameters are the same as in D and the set sizes correspond with the values of pi in D. The predicted set size effect (right panel) is qualitatively similar to set size effects observed in empirical data (cf. panel C). (D) and (E) are alternative illustrations of the same optimization problem; the right panel of (E) could also be obtained by replotting the right panel of (D) as a function of N = 1/pi.
Figure 2—figure supplement 1
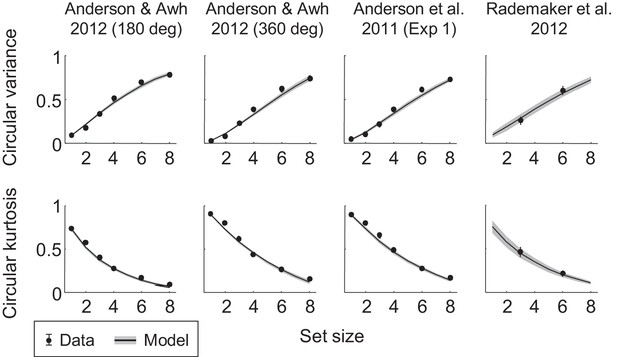
Fits to the three delayed-estimation benchmark data sets that were excluded from the main analyses.
Circular variance (top) and circular kurtosis (bottom) of the estimation error distributions as a function of set size, split by experiment. Error bars and shaded areas represent 1 s.e.m. of the mean across subjects. The first three data sets were excluded from the main analyses on the grounds that they were published in papers that were later retracted (Anderson and Awh, 2012; Anderson et al., 2011). The data set from the study by Rademaker et al. (2012) was excluded from the main analyses because it contains only two set sizes, which makes it less suitable for a fine-grained study of the relationship between encoding precision and set size.
Figure 3
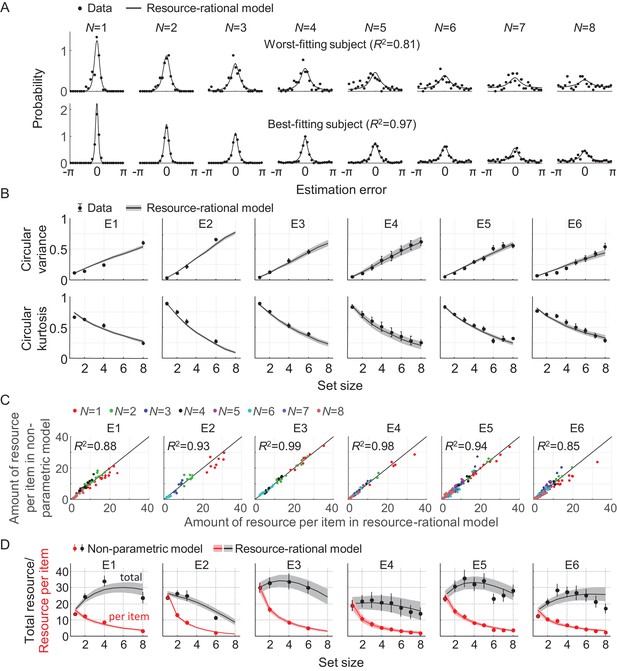
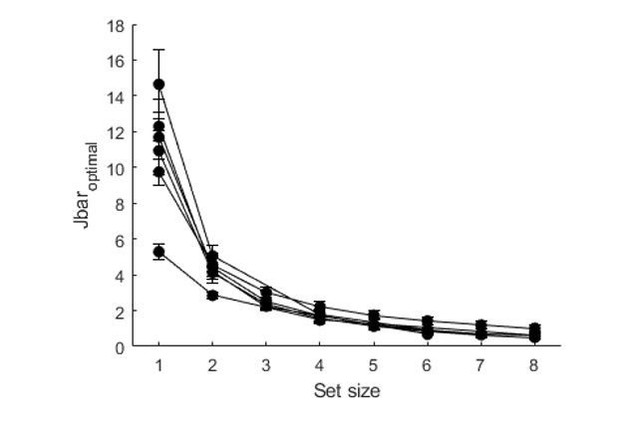
Model fits to data from six delayed-estimation experiments with equal probing probabilities.
(A) Maximum-likelihood fits to raw data of the worst-fitting and best-fitting subjects (subjects S10 in E6 and S4 in E4, respectively). Goodness of fit was measured as R2, computed for each subject by concatenating histograms across set sizes. (B) Subject-averaged circular variance and kurtosis of the estimation error, as a function of set size and split by experiment. The maximum-likelihood fits of the model account well for the trends in these statistics. (C) Estimated amounts of resource per item in the resource-rational model scattered against the estimates in the non-parametric model. Each dot represents estimates from a single subject. (D) Estimated amount of resource per item (red) and total resource (black) plotted against set size. Here and in subsequent figures, error bars and shaded areas represent 1 s.e.m. of the mean across subjects.
Figure 4
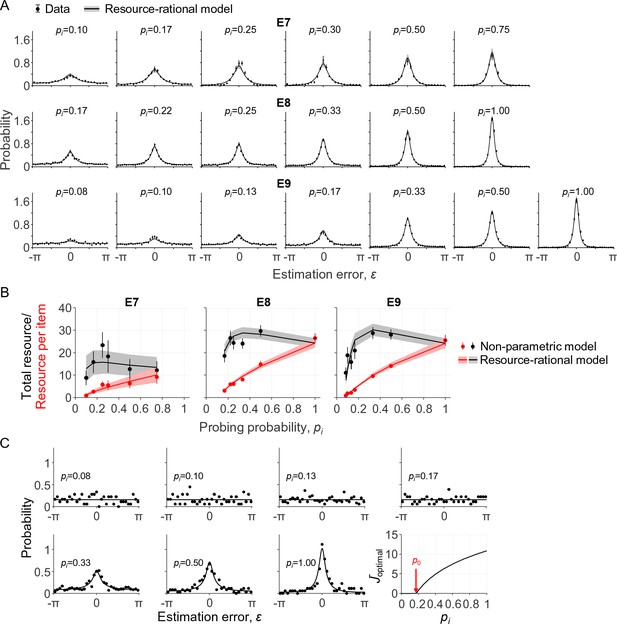
Model fits to data from three delayed-estimation experiments with unequal probing probabilities.
(A) Fits of the resource-rational model (curves) to the data (black circles) of experiments E7-E9. (B) Estimated amount of resource per item as a function of probing probability (red) and the corresponding estimated total amount of resource that the subject would spend on encoding a display filled with items with equal probing probabilities (black). (C) Error histograms and a plot of as a function of pi for a single subject (S4 in E9). The estimated value of p0 was 0.18 for this subject, which was larger than the smallest probing probability in the experiment. The error histograms for items with the four lowest probing probabilities appear to be uniform for this subject, which is indicative of guessing (p>0.23 in Kolgomorov-Smirnov tests for uniformity on these four distributions).
Figure 5
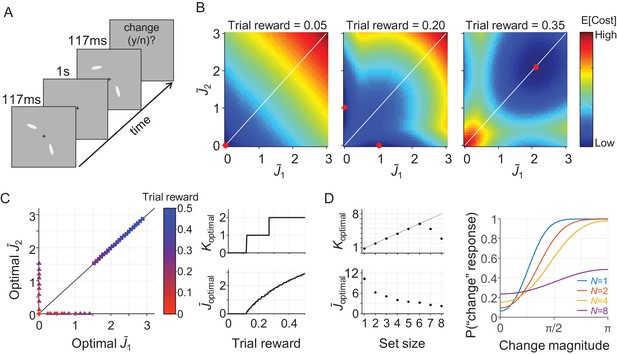
A resource-rational model for change detection tasks.
(A) Example of a trial in a change detection task with a set size of 2. The subject is sequentially presented with two sets of stimuli and reports whether there was a change at any of the item locations. (B) Simulated expected total cost in the resource-rational cost function applied to a task with a set size of 2 and a reward of 0.05 (left), 0.20 (center), or 0.35 (right) units per correct trial. The red dot indicates the location of minimum cost, that is the resource-optimal combination of and (note that the expected cost function in the central panel has a minimum at two distinct locations). When reward is low (left), the optimal strategy is to encode neither of the two stimuli. When reward is high (right), the optimal strategy is to encode both stimuli with equal amounts of resource. For intermediate reward (center), the optimal strategy is to encode one of the two items, but not the other one. (C) Model predictions as a function of trial rewards at N = 2. Left: The amount of resource assigned to the two items for a range of reward values. Right: the corresponding optimal number of encoded items (top) and optimal amount of resource per encoded item (bottom) as a function of reward. (D) Model predictions as a function of set size (trial reward = 1.5). The model predicts set size effects in both the number of encoded items (left, top) and the amount of resource with which these items are encoded (left, bottom). Moreover, the model produces response data (right) that are qualitatively similar to human data (see, for example, Figure 2C in Keshvari et al., 2013). The parameter values used in all simulations were λ = 0.01 and τ↓0.
Figure 6
Model predictions for a delayed-estimation task with binary feedback (N = 5).
In this experiment, the observer receives positive feedback (e.g. "correct") when their estimation error is smaller than the positive feedback threshold and negative feedback (e.g. "error") otherwise. We modelled this using a behavioral cost function that maps errors below the feedback threshold to a cost of 0 and errors larger than this threshold to a cost equal to 1. The model predicts that subjects do not invest any resource when the feedback threshold is very small (extremely difficult tasks) or very large (extremely easy tasks), such that the expected absolute estimation error is π/2 (guessing). In an intermediate regime, the prediction is U-shaped and contains a region in which the predicted estimation error barely changes as a function of feedback threshold. In this region, any performance benefit from increasing the amount of invested resource is almost exactly outdone by the added neural cost. The dashed lines show the feedback thresholds corresponding to the "high precision" and "low precision" conditions in the experiment by Nassar et al. (2018). Under the chosen parameter settings (λ = 0.08, τ = 30), the model predicts that the average absolute estimation errors in these two conditions (black circles) are very similar to each other.
Appendix 1—figure 1
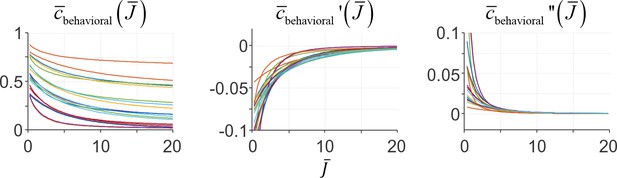
Examples of the expected behavioral cost function and its first and second derivative under a behavioral cost function cbehavioral(ε)=|ε|β.
Different colors represent different choices of parameters β and τ (randomly drawn).
Appendix 1–figure 2
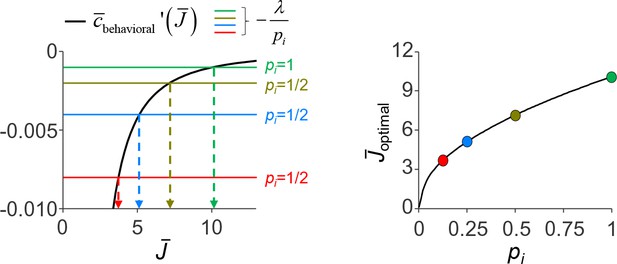
Graphical illustration of the solution to the cost-minimization problem that determines the value of .
The cost-minimizing value of solution of lies at the intersection between the derivative of the expected behavioral cost function (black curve) and a flat line at a value –λ/pi (colored lines). This value (indicated with arrows) necessarily increases with pi. The parameter values used in this simulation were the same as those used to generate Figure 2D and E (λ = 0.01, β = 2, τ↓0).
Author response image 1
Tables
Table 1
Overview of experimental datasets.
Experiments E5 and E6 differed in the way that subjects provided their responses (E5: color wheel; E6: scroll).
| Exp. ID | Reference | Feature | Set size(s) | Probing probability | Number of subjects |
|---|---|---|---|---|---|
| E1 | Wilken and Ma (2004) | Color | 1, 2, 4, 8 | Equal | 15 |
| E2 | Zhang and Luck (2008) | Color | 1, 2, 3, 6 | Equal | 8 |
| E3 | Bays et al. (2009) | Color | 1, 2, 4, 6 | Equal | 12 |
| E4 | van den Berg et al. (2012) | Orientation | 1-8 | Equal | 6 |
| E5 | van den Berg et al. (2012) | Color | 1-8 | Equal | 13 |
| E6 | van den Berg et al. (2012) | Color | 1-8 | Equal | 13 |
| E7 | Bays et al. (2009) | Orientation | 2,4,8 | Unequal | 7 |
| E8 | Emrich et al. (2017) | Color | 4 | Unequal | 20 |
| E9 | Emrich et al. (2017) | Color | 6 | Unequal | 20 |
Table 2
Subject-averaged parameter estimates of the resource-rational model fitted to data from nine previously published experiments.
See Table 1 for details about the experiments.
| Experiment | β | λ | τ |
|---|---|---|---|
| E1 | 1.87 ± 0.29 | (4.8 ± 1.2)·10−2 | 17.9±2.5 |
| E2 | (1.33 ± 0.30)·10−2 | (4.27 ± 0.83)·10−4 | 14.8±1.1 |
| E3 | 0.138 ± 0.042 | (2.78 ± 0.87) ·10−3 | 19.1±2.6 |
| E4 | 0.106 ± 0.052 | (3.2 ± 1.4)·10−3 | 8.2±1.8 |
| E5 | 0.356 ± 0.085 | (5.8 ± 1.1)·10−3 | 18.1±2.8 |
| E6 | 0.61 ± 0.15 | (8.8 ± 1.5)·10−3 | 7.4±1.3 |
| E7 | 1.19 ± 0.51 | (9.5 ± 6.6)·10−2 | 5.7±1.5 |
| E8 | 0.58 ± 0.19 | (1.58 ± 0.66)·10−2 | 27.0±3.7 |
| E9 | 0.93 ± 0.25 | (3.0 ± 1.0)·10−2 | 23.7±2.3 |
Table 3
Comparing two metrics for model comparison: AIC and five-fold cross-validated log likelihood.
Each comparison is between the main version of the resource-rational model, Equation (11), and the model listed in the first column of the table. Negative AIC differences and positive cross-validated log likelihood differences indicate an advantage of the resource-rational model over the alternative model. In all comparisons, these differences have opposite signs, which means that the AIC-based results are consistent with the cross-validation results.
| Model with which the main model is compared | AIC difference | Cross-validation log likelihood difference |
|---|---|---|
| Descriptive power-law model | −5.27±0.70 | 2.59±0.39 |
| Descriptive fixed-resource model | −13.9±1.4 | 8.4±1.0 |
| Descriptive unconstrained model | 3.49±0.93 | −1.26±0.49 |
| Rational model variant: equal precision | −110±10 | 56±4.7 |
| Rational model variant: cbehavioral=|ε| | −14±2.8 | 7.1±1.4 |
| Rational model variant: cbehavioral=ε2 | −24.4±4.1 | 12.2±2.0 |
| Rational model variant: cbehavioral=−cos(ε) | −19.5±3.5 | 9.8±1.8 |
| Rational model variant: cbehavioral as in Sims (2015) | −5.3±1.8 | 4.7±0.74 |
Table 4
Examples of resource-rationality concepts in neuroscience, psychology, and economics.
https://doi.org/10.7554/eLife.34963.013| Study | Optimized quantity | Performance term | Resource cost/constraint |
|---|---|---|---|
| Efficient coding in neural populations | |||
| Ganguli and Simoncelli (2010) | Tuning curve spacing and width | Fisher information or discriminability | Neural activity (constraint) |
| Olshausen and Field (1996) | Receptive field specificity | Information | Sparsity |
| Capacity “limitations” in attention and memory | |||
| Sims et al. (2012) | Information channel bit allocation | Channel distortion (e.g. squared error) | Channel capacity (constraint) |
| Van den Berg and Ma (present study) | Mean encoding precision | Behavioral task accuracy | Neural activity (cost) |
| Rational inattention in consumer choice | |||
| Sims (2003) | Distribution of attention | Channel distortion (e.g. squared error) | Channel capacity (constraint) |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.34963.014
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
A resource-rational theory of set size effects in human visual working memory
eLife 7:e34963.
https://doi.org/10.7554/eLife.34963
