Characterisation of molecular motions in cryo-EM single-particle data by multi-body refinement in RELION
- MRC Laboratory of Molecular Biology, United Kingdom
- Stockholm University, Sweden
- Swedish e-Science Research Center, KTH Royal Institute of Technology, Sweden
Figures
Figure 1 with 2 supplements
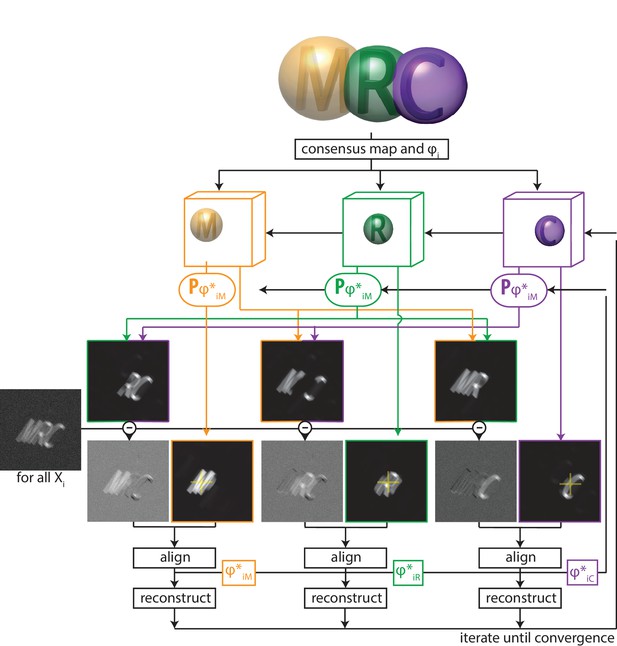
A schematic overview of multi-body refinement.
After a consensus 3D auto-refinement in RELION, the three-dimensional consensus map is split into separate bodies using user-defined masks. In this example, and the letters ’M’ (orange), ’R’ (green) and ’C’ (puple) each represent a body, and the corresponding spherical masks are shown with transparency. During multi-body refinement, one performs focused refinement for all experimental particle images , with local rotational and translational searches around the orientations from the consensus refinement. The yellow crosses in the reference projections for the focused refinements of each body indicate the centre-of-mass of each body’s mask, around which all rotations are made.For each body, partial signal subtraction is performed with projections along the current estimates for the respective orientations of the other bodies. This leads to subtracted versions of each experimental particle image during every iteration, which are aligned against projections of the corresponding body. The resulting optimal orientations for each body are used for the partial signal subtraction in the next iteration. Iterative alignment and reconstruction of all three bodiesis is repeated until convergence, which is when resolutions no longer improve and changes in the relative orientations of all bodies become small.
-
Figure 1—source data 1
The body definition STAR file.
Example of a STAR file that defines the bodies in Figure 1. The column labelled rlnBodyMaskName defines the file names for the corresponding masks; the relative orientations of eachbody are defined by the columns (rlnBodyRotateRelativeTo); and the priors on the rotations and translations of the bodies are given by rlnBodySigmaAngles and rlnBodySigmaOffset, respectively.
- https://doi.org/10.7554/eLife.36861.005
Figure 1—figure supplement 1
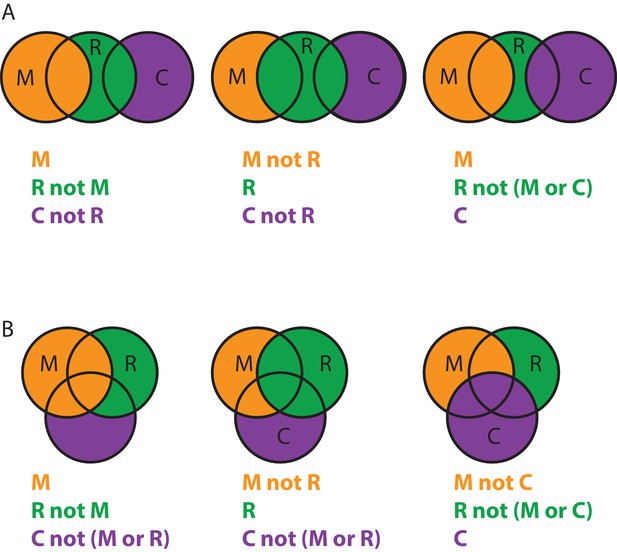
Overlapping body masks.
(A) Overlapping masks for the example shown in Figure 1. For the partial signal subtraction for focused refinement of the ’M’ body, the density of the ’R’ body within the ’R’ mask but not within the ’M’ mask will be subtracted, together with the density of the ’C’ body within the ’C’ mask, but not within the ’R’ mask (left). Partial signal subtraction for focused refinement of the ’R’ body comprises the density of the ’M’ body within the ’M’mask that does not overlap with the ’R’ mask and the density of the ’C’ body within the ’C’ mask that does not overlap with the ’R’ mask (middle). Similarly, for focused refinement of the ’C’ body, partial signal subtraction comprises the density of the entire ’M’ body and the density of the ’R’ body within the ’R’ mask that does not overlap with either the ’M’ mask or the ’C’ mask. A total of seven different masked maps needs to be stored in computer memory. (B) As in A, but for an example whereall three masks overlap with each other. A total of nine different masked maps needs to be stored in computer memory.
Figure 1—figure supplement 2
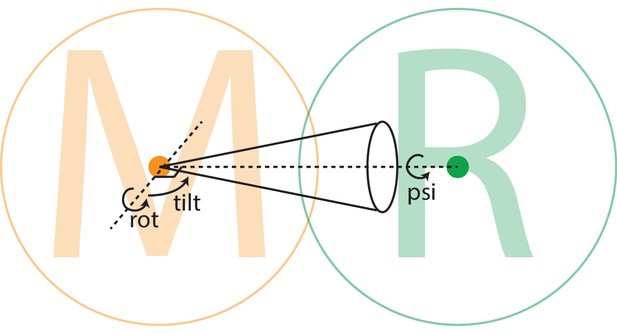
Relative body orientations.
The density for each body is placed with the centre-of-mass of its mask (indicated with orange and green dots for the ’M’ body and ’R’ body, respectively) at the centre of the three-dimensional box, and all rotations are around this centre. Each body rotates relative to a neighbouring body, as defined using the rlnBodyRotateRelativeTo column in the input body STAR file (Figure 1—source data 1). In this example, the ’M’ body rotates relative to the ’R’ body. The rotation is expressed in Euler angles around an axis perpendicular to the vector between the centre-of-mass of the two bodies to prevent ambiguities in Euler-angle definitions around zero values for the second Euler angle (tilt). The cone illustrates the width at half the maximum value (FWHM) of a Gaussian-shaped prior on the rot-tilt tuple. A separate Gaussian-shaped prior exists on the third Euler angle (psi).
Figure 2 with 1 supplement
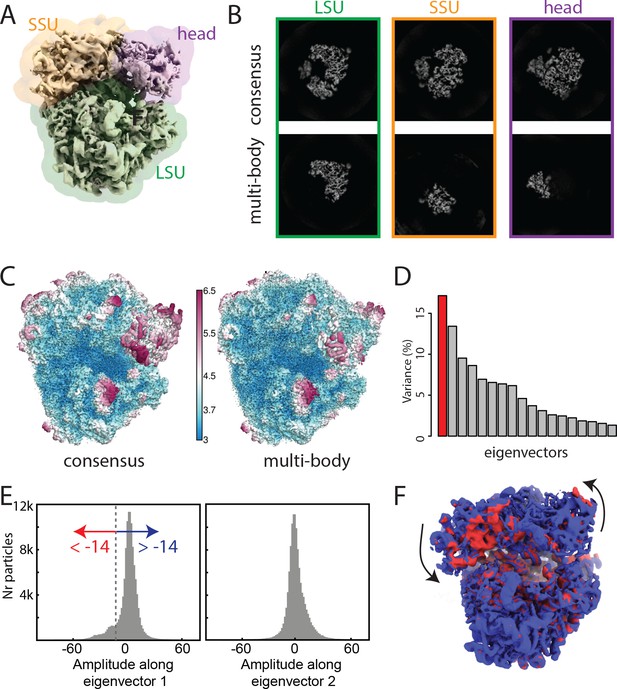
The ribosome test case.
(A) The ribosome consensus map with the three transparent body masks (LSU, SSU and head) superimposed. (B) Slices through the density of the three bodies after the consensus refinement (top) and after multi-body refinement (down). (C) Local resolution estimates (in Å) calculated in relion after the consensus refinement (left) and after multi-body refinement (right). (D) The contributions of all eigenvectors to the variance. The first eigenvector, for which the maps at the extremes are shown in panel F, is highlighted in red. (E) Histograms of the amplitudes along the first and second eigenvectors for all particle images in the data set. The histogram of the amplitudes along the first eigenvector shows a bimodal distribution. The data set was split into two subsets: particle images with the amplitude along the first eigenvector smaller than −14 (red arrow) and particle images with that amplitude larger than −14 (blue arrow). (F) Refined maps for the two subsets in the same colors. As observed in the movie along the first eigenvector, the SSU rolls with respect to the the LSU and the head swivels with respect to the SSU, cf Video 1.
Figure 2—figure supplement 1
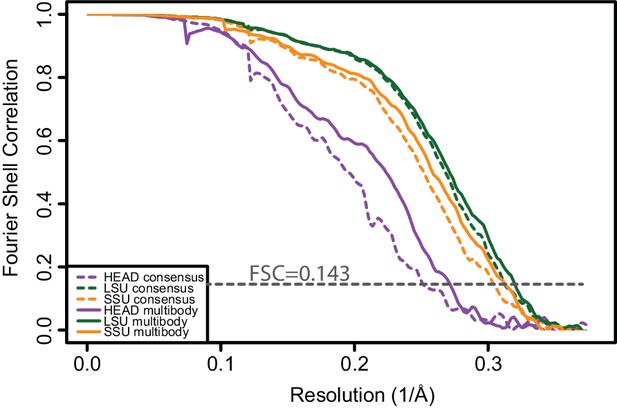
Fourier shell correlation curves calculated from independently refined halves of the data for the three bodies after consensus refinement (dashed lines) and after the second multi-body refinement (solid lines).
https://doi.org/10.7554/eLife.36861.007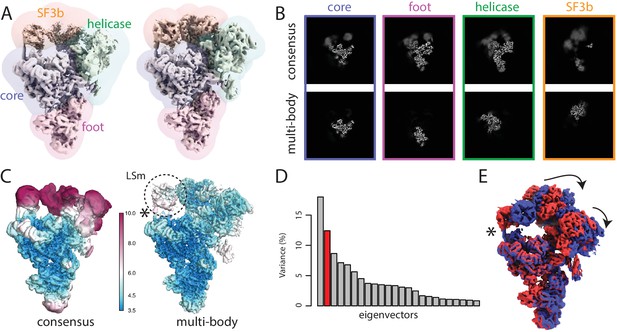
Figure 3 with 3 supplements
The spliceosome test case.
(A) The four body masks used for the first splicesome multi-body refinement are shown in semi-transparent colours on top of the consensus map on the left; the resulting density after the first multi-body refinement and the masks used for the second multi-body refinement are shown on the right. (B) Slices through the density of the four bodies after the consensus refinement (top) and after multi-body refinement (down). (C) Local resolution estimates (in Å) calculated in RELION after the consensus refinement (left) and after multi-body refinement (right). (D) The contributions of all eigenvectors to the variance. The second eigenvector, for which the maps at the extremes are shown in panel E, is highlighted in red. (E) Motion represented by the second eigenvector, cf Video 4. The helix that connects the core of the spliceosome and the LSm ring of the SF3b body that gets broken during the repositioning of the bodies in the eigenvector movies and the combined maps is indicated with an asterisk (also see main text).
Figure 3—figure supplement 1
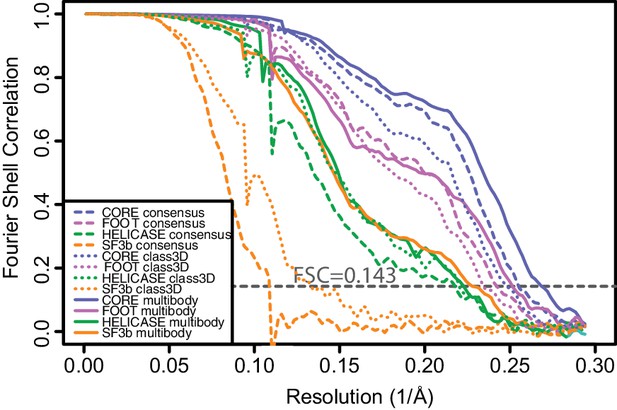
Fourier shell correlation curves calculated from independently refined halves of the data for the four bodies after consensus refinement (dashed lines), for the largest class of a discrete 3D classification (dotted lines) and after the second multi-body refinement (solid lines).
https://doi.org/10.7554/eLife.36861.011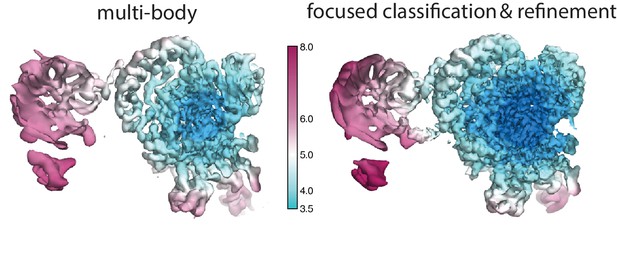
Figure 3—figure supplement 2
Local resolution estimates (in Å) for the SF3b region after multi-body refinement (left) and after subsequent partial signal subtraction in relion_flex_analyse followed by focused classification and refinement of the best class (right).
https://doi.org/10.7554/eLife.36861.012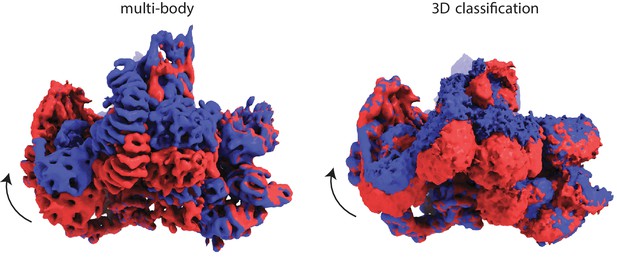
Figure 3—figure supplement 3
The largest two classes of a 3D classification with eight classes (right) represent a similar motion as identified by the first principal component from the multi-body approach (left).
For the latter, the third and eight out of ten movie frames are shown.
Videos
Video 1
Repositioning of the reconstructed body densities along the first eigenvector for the ribosome case reveals a rolling-like motion of the SSU with respect to the LSU and a concomitant swiveling of the head.
https://doi.org/10.7554/eLife.36861.008
Video 2
Repositioning of the reconstructed body densities along the second eigenvector for the ribosome case reveals a ratchet-like motion of the SSU with respect to the LSU together with a displacement of the head.
https://doi.org/10.7554/eLife.36861.009
Video 3
Repositioning of the reconstructed body densities along the first eigenvector for the spliceosome case reveals a rocking motion of the SF3b domain over the core.
https://doi.org/10.7554/eLife.36861.014
Video 4
Repositioning of the reconstructed body densities along the second eigenvector for the spliceosome case reveals a concerted rocking motion of the helicase and SF3b over the core.
https://doi.org/10.7554/eLife.36861.015Tables
Key resources table
| Reagent type | Designation | Reference | Identifier |
|---|---|---|---|
| software | relion | (Scheres, 2012b) | RRID:SCR_016274 |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Characterisation of molecular motions in cryo-EM single-particle data by multi-body refinement in RELION
eLife 7:e36861.
https://doi.org/10.7554/eLife.36861
