Value-based attentional capture affects multi-alternative decision making
- University of Basel, Switzerland
- University of Freiburg, Germany
Figures
Figure 1 with 1 supplement
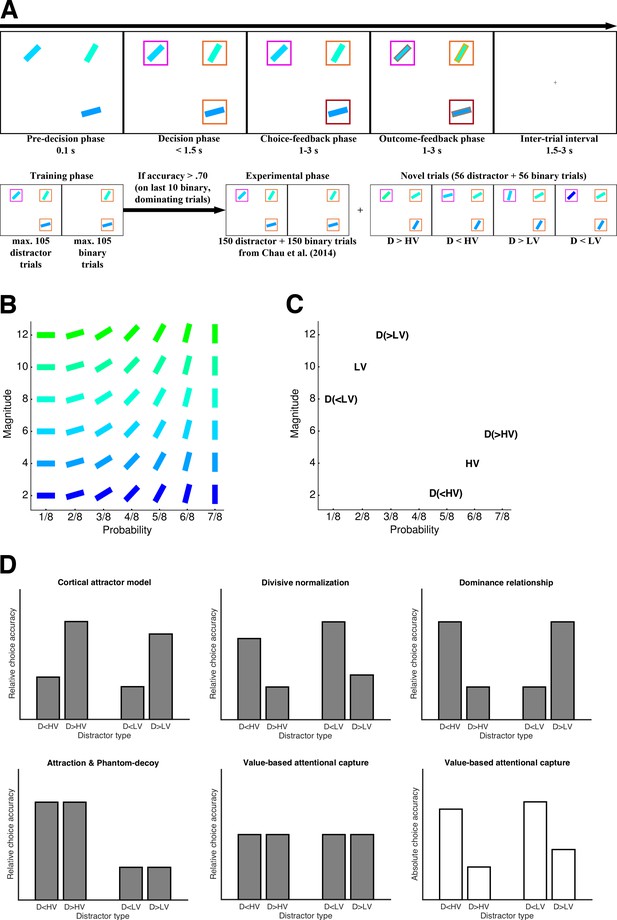
Study design and predictions for novel trials.
(A) Example trial (upper panel) and general workflow (lower panel) of the Chau2014 paradigm as used in our four experiments (variations in specific experiments are mentioned in the main text). In the critical trials, participant had 1.6 s to choose between two rectangles with a third rectangle displayed but declared unavailable after 0.1 s. (B) Stimulus matrix showing one (of four possible) associations of color and orientation of rectangles with reward probability and magnitude. (C) Example of a set of four novel trials (HV and LV were kept constant across these four trials, but D varied). (D) Qualitative predictions of choice accuracy in the novel trials for the biophysical cortical attractor model proposed by Chau2014, the divisive normalization model proposed by Louie2013, various ‘context effects’ (see Materials and methods), and value-based attentional capture. The predictions vary with respect to the factors Similarity (i.e., whether D is more similar to HV or to LV) or Dominance (i.e., whether D is better or worse than HV/LV). In contrast to the other models, value-based attentional capture does not predict any influence of D’s value on relative choice accuracy (grey bars) but a detrimental effect on absolute choice accuracy (white bars). Predictions of absolute choice accuracy for the remaining models are provided in Figure 1—figure supplement 1.
Figure 1—figure supplement 1
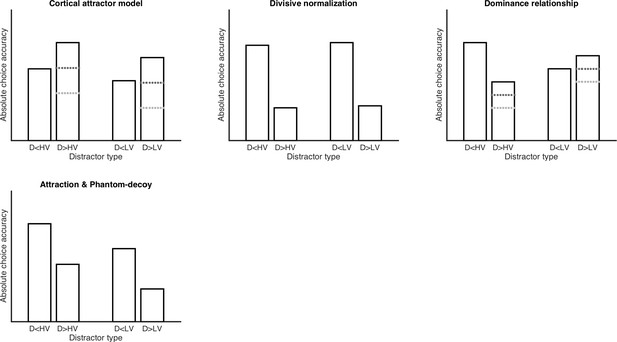
Qualitative predictions of absolute choice accuracy for alternative models.
Under the assumption that the distractor D is treated as a regular choice option (see Discussion), all models would predict that high-value D are chosen more often than low-value D, so that absolute choice accuracy in the novel trials with D > HV and D > LV are lowered compared to D < HV and D < LV. For the cortical attractor model proposed by Chau2014, however, it is unclear whether this effect reduces, levels out, or reverses the (opposing) effect on relative choice accuracy (as indicated by the dark- and light-gray dotted lines). Similarly, for the dominance relationship hypothesis, it is unclear whether absolute choice accuracy for D < LV will be lower, equal or higher than for D > LV (note that these are only qualitative and not exact quantitative predictions of the models).
Figure 2
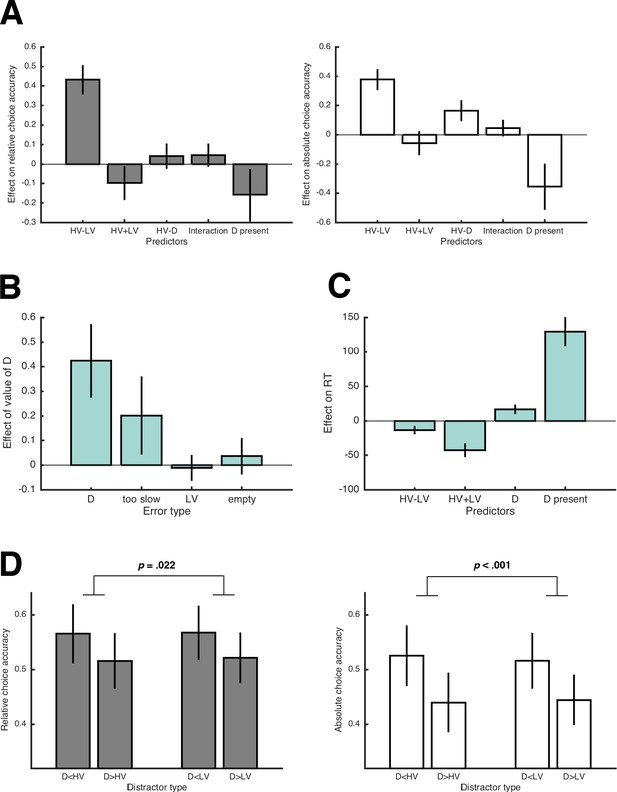
Results of Experiment 1.
(A) Average regression coefficients of the predictor variables proposed by Chau2014 (including the HV-D predictor, which had a negative coefficient in their data) for relative and absolute choice accuracy (left and right panel, respectively). The term ‘interaction’ refers to the predictor variable (HV-LV)×(HV-D). Note that error bars in all figures represent 95% CIs, so that error bars not crossing the 0-line indicate significant effects. (B) Average coefficients of (separate) regression analyses testing how the value of D influenced different types of errors. (C) Average regression coefficients of predictor variables that influenced RT. (D) Relative and absolute choice accuracy in the novel trials (compare with predictions in Figure 1D). The comparatively low performance in the novel trials is due to HV and LV having very similar expected values (see Figure 1C).
Figure 3
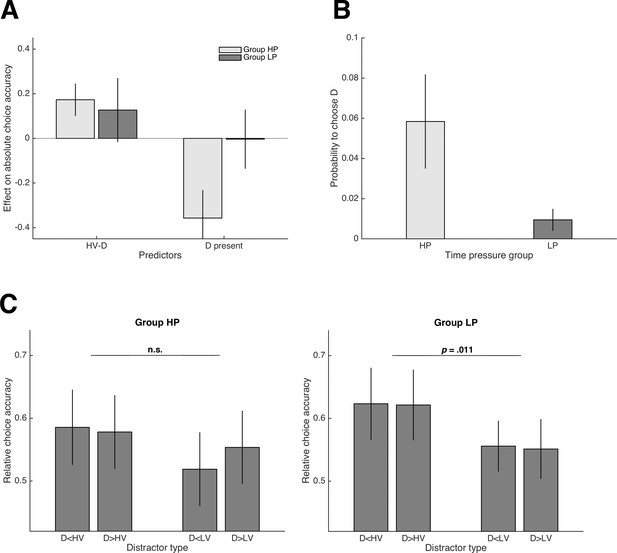
Results of Experiment 2.
(A) Group comparison of regression coefficients reflecting the influence of HV-D and the presence of D on absolute choice accuracy (HP = high time pressure, LP = low time pressure). (B) Group comparison of the frequency of choosing D. In general, the negative influence of D on performance diminished substantially in Group LP, who made decisions under low time pressure. (C) Relative choice accuracy in the novel trials for Group HP (left panel) and LP (right panel). A violation of IIA was only observed in Group LP and is consistent with a combined attraction and phantom-decoy effect (compare with predictions in Figure 1D; see also Materials and methods).
Figure 4 with 1 supplement
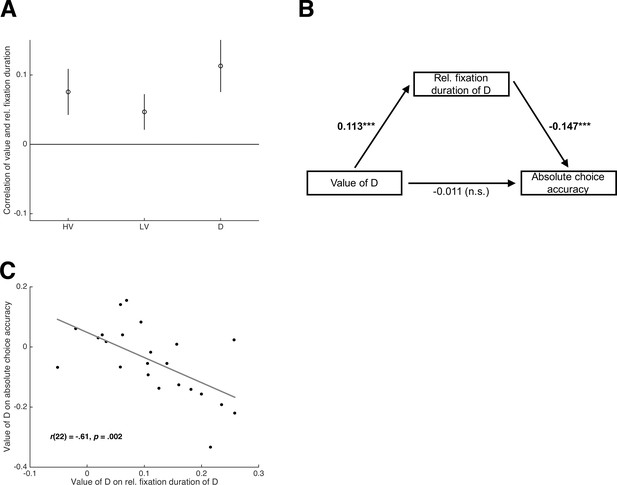
Eye-tracking results of Experiment 3.
(A) Average coefficients for the correlation of the value of HV, LV, and D with the relative fixation duration on HV, LV, and D. (B) Path analysis of the relationship between the value of D, the attention on D (i.e., relative fixation duration of D), and absolute choice accuracy. The path analysis is conducted within each participant; the numbers represent the average path coefficients (tested against 0; ***p < .001). (C) Across-participant correlation of the coefficients representing the (positive) influence of the value of D on attention on D and the (negative) influence of the value of D on absolute choice accuracy.
Figure 4—figure supplement 1
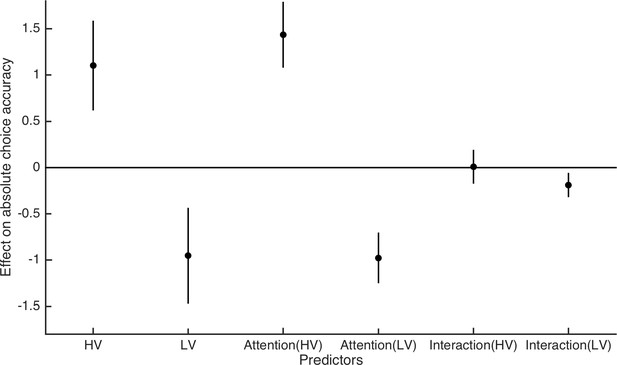
Testing the influence of attention on choice.
Depicted are the average regression coefficients for the predictor variables of the expected values (EVs) of HV and LV, the relative fixation durations of HV and LV (‘Attention’), and the interaction of the EVs and relative fixation durations (‘Interaction’) on absolute choice accuracy (i.e., on whether HV was chosen or not). The direct effects of attention to HV and LV were both significant. From the interaction terms, only the LV-interaction (but not the HV-interaction) was significant. Replacing the first two predictor variables by a single value difference variable (i.e., HV-LV) yields equivalent results.
Figure 5 with 5 supplements
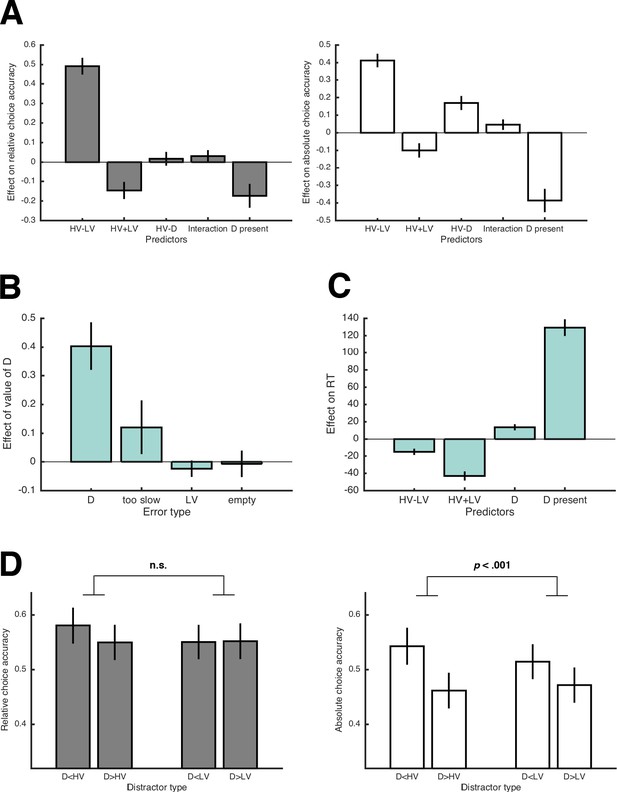
Summary of behavioral results of Experiment 1 to 4.
(A) to (D) are analogous to Figure 2 but collapsed over all experiments conducted under high time pressure. Results in (D) only contain data from Experiment 1 to 3, because novel trials were omitted in Experiment 4.
Figure 5—figure supplement 1
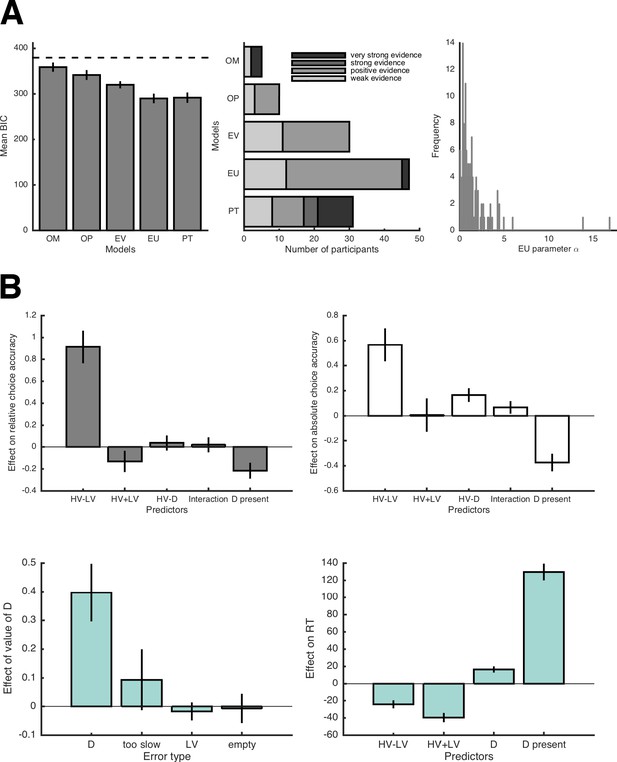
Testing the assumption that participants decided on the basis of expected values (EVs).
(A) Model comparison between simple choice models predicting whether HV or LV was chosen (OM = Only Magnitude model; OP = Only Probability model; EV = Expected Value model; EU = Expected Utility model; PT = Prospect Theory model). The left panel shows average BIC values (lower values indicate better predictions; the dashed line indicates the BIC value of a ‘chance level’ model that predicts each choice with p = 0.5). The middle panel shows model evidence per participant. The EU model appears to provide the most parsimonious account of the data. The right panel shows the distribution of the power utility parameter α of the EU model. There are some very high values, possibly reflecting participants who primarily focused on the magnitude information when making decisions. (B) Reanalysis of the main behavioral results (shown in Figure 5) when replacing EV by EU-based subjective value estimates. Largely, the results do not change (i.e., no effect of HV-D on relative choice accuracy; positive effect of HV-D on absolute choice accuracy; higher values of D increase choices of D and RTs). Only the effect of D’s value on too-slow errors did not reach significance anymore (p = .077).
Figure 5—figure supplement 2
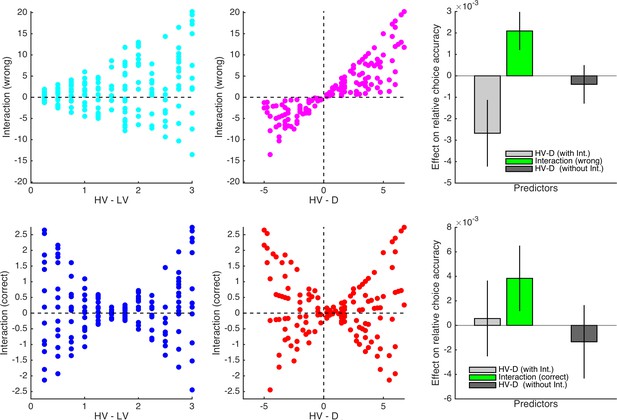
The influence of the interaction term (HV-LV)×(HV-D) on the estimation of the HV-D effect.
The upper row refers to the incorrect interaction term that is generated based on uncentered HV-LV and HV-D; the lower row refers to the correct interaction term that is generated based on standardized HV-LV and HV-D. The first two columns show correlations between the interaction terms and HV-LV/HV D, respectively. The last column shows the mean regression coefficients of 1’000 simulations of 21 decision makers whose choices depend only on HV-LV. Only when the incorrect interaction term is included is the HV-D coefficient biased in the negative direction. Note that both incorrect and correct interaction terms are estimated to be positive, which is another statistical artifact and results from the positive correlation between the predictors HV-LV and HV-D (r = .138; simulations with uncorrelated HV-D and HV-LV predictors do not exhibit this statistical artifact).
Figure 5—figure supplement 3
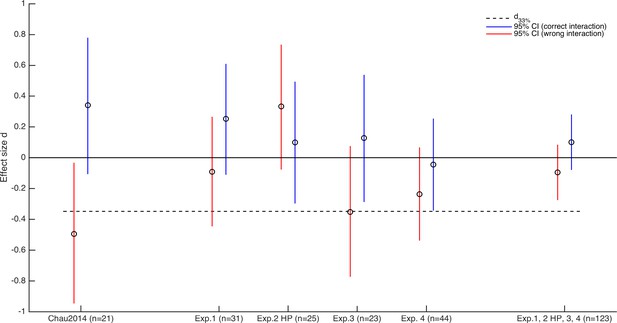
Effect sizes and test of detectability.
Depicted are the effect sizes and their 95% and 90% CIs of the HV-D effect on relative choice accuracy for the Chau2014 dataset, for Experiment 1, 2 (Group HP), 3, and 4, and for all four experiments combined, separately for analysis with correct (blue) and incorrect (red) implementation of the interaction term (see Materials and methods). The black dashed line indicates the d33% effect size (i.e., the effect size at which the Chau2014 study with 21 participants would have only 33% statistical power to detect an effect). According to Simonsohn (2015), if the CIs of the effect size in the replication study do not overlap with d33%, then it is unlikely that such an effect was detectable with the original sample size. Note that the HV-D effects are generally lower when using the incorrect interaction term (except for Experiment 2 HP). But even in this case, the data would be best explained as a null finding.
Figure 5—figure supplement 4
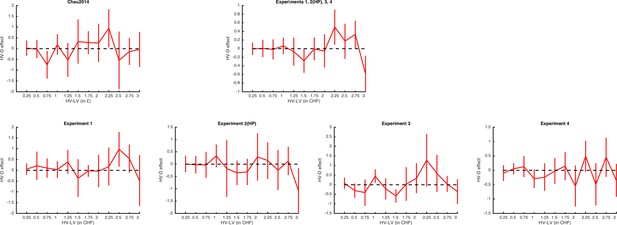
Analysis of the HV-D effect on relative choice accuracy for different levels of HV-LV.
Depicted is the effect of HV-D on relative choice accuracy when the regression analyses are conducted separately for each of the 12 HV-LV differences for the Chau2014 data, for all our experiments combined, and for each of our four experiments separately. A robust HV-D effect was not obtained in any of our own experiments but also not in the Chau2014 dataset. For the latter, the HV-D effect is significantly negative in one level of HV-LV but also significantly positive in another level. According to Chau2014, the effect might be more pronounced in difficult trials, but even when restricting the analysis to the more difficult half of the trials (i.e., to the six bins with the lowest HV-LV difference), there is no significantly negative HV-D effect (t(20) = −1.23, p = .245). These results provide further evidence that the incorrect implementation and inclusion of the interaction term is the main reason for the HV-D effect being significantly negative in the analysis reported in Chau2014.
Figure 5—figure supplement 5
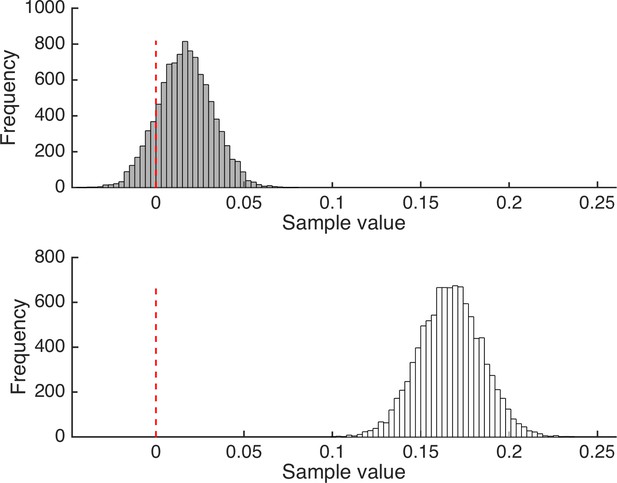
Bayesian analyses of the HV-D Effect on relative and absolute choice accuracy.
(A) Histogram of posterior samples from a Bayesian t-test for the HV-D regression coefficients on relative choice accuracy. The analysis includes the coefficients from all 123 participants that conducted the task with short deliberation time (as in Chau2014). As can be seen, the posterior distribution largely overlaps with 0 (highlighted by the red dashed line). (B) The same analysis for absolute choice accuracy. Here, there is almost no overlap with 0.
Figure 6 with 1 supplement
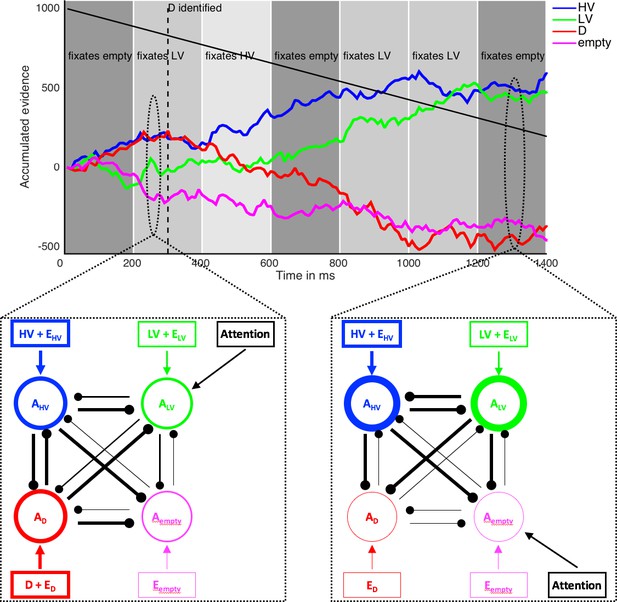
Illustration of the computational model MIVAC.
Depicted is the development of accumulators of the MIVAC model with estimated parameters from a representative example participant in an example trial (upper panel) together with schematic outlines of the model at two different time points (lower panels). MIVAC consists of four accumulators representing HV, LV, D, and the empty quadrant. At every time step, each accumulator Ax (round nodes in lower panels) receives an input (rectangular nodes) that is equal to the expected value of x (set to 7.5, 5, 10.5, and 0 in this example), plus Gaussian noise Ex. Accumulators inhibit each other (connecting lines between round nodes). Thicker round nodes, rectangular nodes/arrows, and lines indicate higher accumulation states, input, and inhibition, respectively. A choice is made as soon as an accumulator reaches an upper boundary that decreases with time (decreasing black line in upper panel). In this example, HV is chosen after ~900 ms. After D is identified (at 300 ms in this example; dashed vertical line in upper panel), the value of D does not serve as an input to its accumulator anymore. Every 200 ms, a new fixation is made (background greyscale), and the accumulator of the currently fixated option receives an additional input (black ‘Attention’ rectangular nodes). According to the value-based attentional capture element of MIVAC, the probability of fixating an option depends on its (relative) value.
Figure 6—figure supplement 1
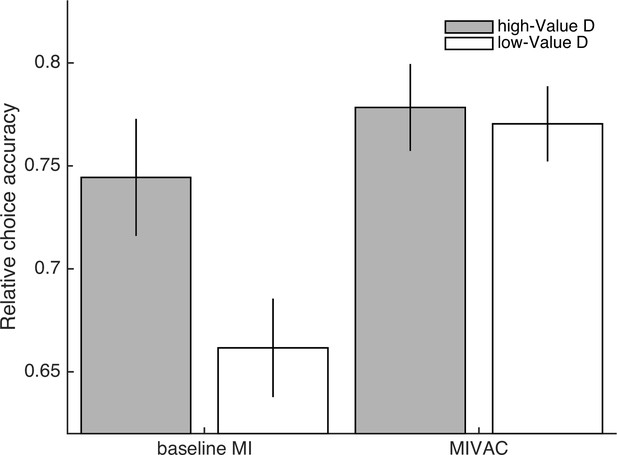
The influence of D on relative choice accuracy in the MI and MIVAC models.
Depicted is the relative choice accuracy of the baseline MI model and the MIVAC model when a high- or a low-value D is present. The values are based on 20 repetitions of 150 simulations of two example trials with the following expected values: HV = 7.5, LV = 5, high-value D = 10.5, low-value D = 0.25. We used the estimated parameters of a representative participant (i.e., the participant whose parameter estimates were closest to the group mean). Similar to the biophysical attractor model proposed by Chau2014, the baseline MI predicts that the relative choice accuracy is higher when a high-value D is present (p < .001). In contrast, MIVAC does not predict this effect (p = .548).
Figure 7 with 5 supplements
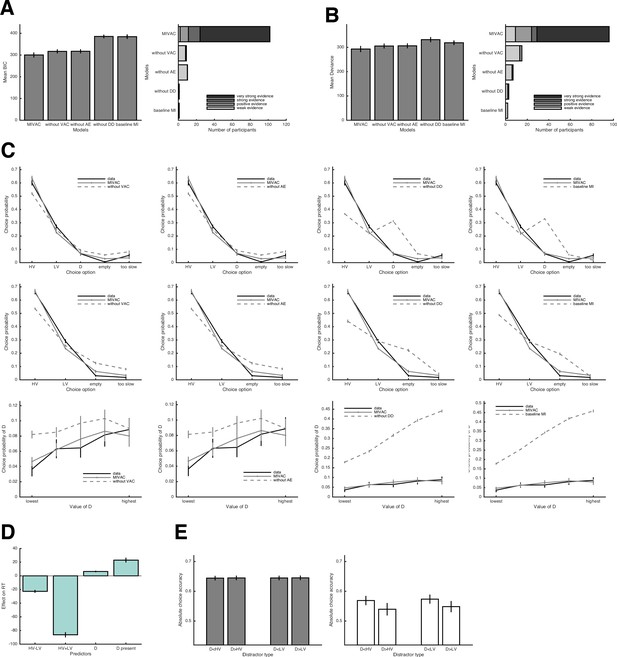
Quantitative and qualitative tests of MIVAC.
(A) Left panel: average model fits for MIVAC and its simplifications for trials with D present (BIC = Bayesian Information Criterion; lower BICs indicate better fits). MIVAC had the lowest BIC (p < .001 for all pairwise comparisons). Right panel: model evidence per participant. (B) The same as in (A) but generalized to trials with D absent. MIVAC had the lowest deviance (p < .001 for all pairwise comparisons). (C) Upper panel: choice proportions (black line) for the five potential actions together with predictions of MIVAC (continuous grey line) and one of its variants (dashed grey lines). Middle panel: the same but for trials with D absent. Lower panel: observed and predicted probabilities of choosing D as a function of D’s value. It can be seen that the variants of MIVAC without value-based attentional capture or attention-based enhancement of value accumulation fail to predict that choices of D increase as D’s value increases. In contrast, the other two variants (i.e., without detection of D, baseline MI) predict too many choices of D. (D) Predicted RT effects of the value of D by MIVAC; the model correctly predicts all RT effects observed in the data (see Figure 5C). (E) Generalization of MIVAC to the novel trials; the model reproduces the observed qualitative patterns of both relative and absolute choice accuracy (see Figure 5D).
Figure 7—figure supplement 1
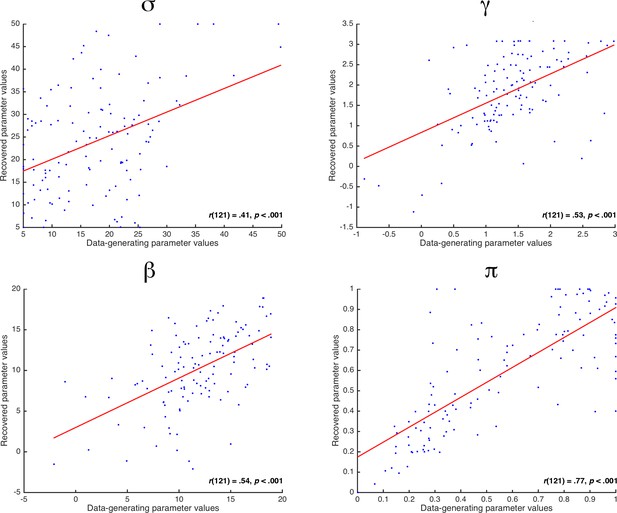
Model recovery results.
Correlations between the data-generating and recovered parameter values for MIVAC’s four parameters. To create realistic testing conditions, the model recovery analysis used the estimated parameters of each participant and generated synthetic data for the 150 trials that were used to fit the model. σ=standard deviation of accumulation, γ = value based attentional capture, β = attention based enhancement of accumulation, π = probability to identify D as being unavailable.
Figure 7—figure supplement 2
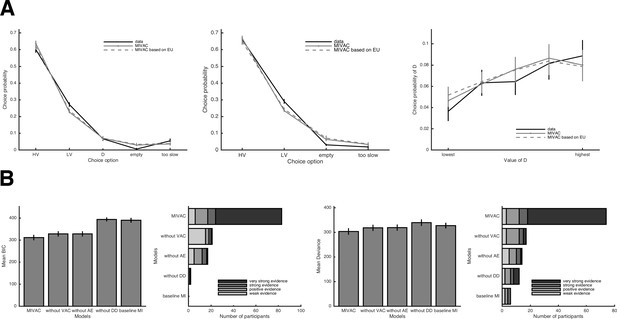
MIVAC with EU-based subjective values as inputs.
(A) Comparison of qualitative predictions of MIVAC with EV or EU-based subjective values as input to the options’ accumulators. The two variants make very similar predictions. (B) Quantitative model comparison between all MIVAC variants with EU-based subjective values. The full model still provides the best account of choices with D present (left panels) and choices with D absent (right panels). Details on the implementation of EU-based subjective values within MIVAC are provided in the Methods.
Figure 7—figure supplement 3
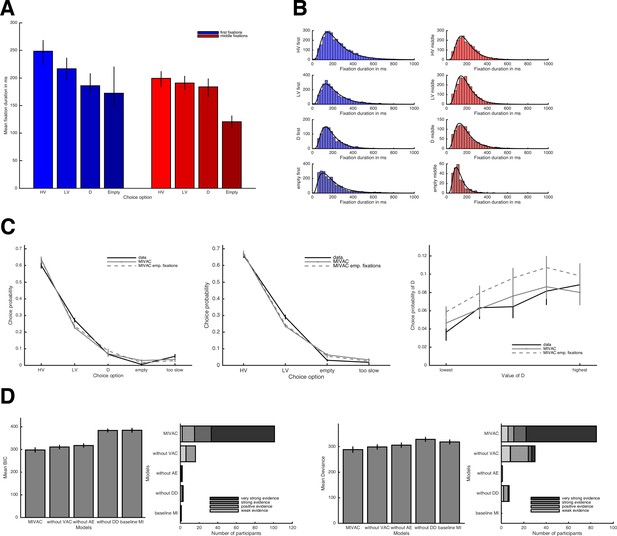
Fixation durations and MIVAC with empirical fixation durations.
(A) Average fixation durations separated by choice option and first vs. middle fixations. (B) Fixation duration histograms separated by choice options and first vs. middle fixations together with fitted log-normal distributions (for the simulations of MIVAC with empirical fixations, durations are samples from these distributions). (C) Comparison of qualitative predictions of MIVAC without and with empirical fixations. The two variants make very similar predictions. (D) Quantitative model comparison between all MIVAC variants with empirical fixations. Using the empirical fixations does not help the simplified variants of MIVAC to catch up with the full model.
Figure 7—figure supplement 4
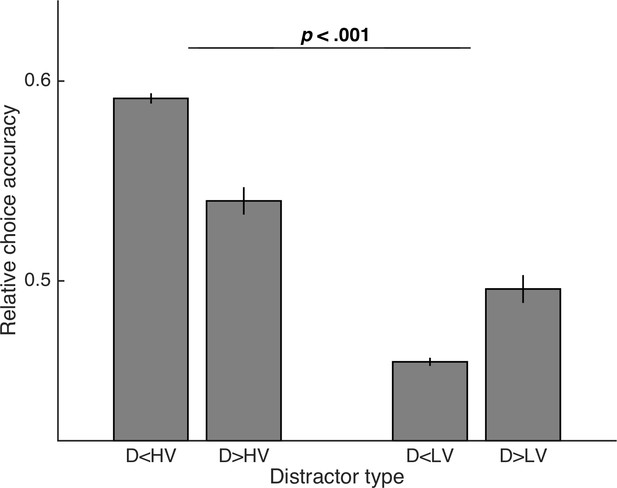
Predictions of IIA violations with extension of MIVAC.
An extended version of MIVAC that includes attribute-wise comparison mechanisms borrowed from the MLBA model (Trueblood et al., 2014) predicts the IIA violation as seen in the variant of the Chau2014 task with long deliberation time (i.e., Experiment 2, Group LP), that is, a higher probability of choosing HV as compared to choosing LV when D is more similar to HV than to LV. Thus, MIVAC belongs to a class of sequential sample models that generally allows accounting for violations of IIA.
Figure 7—figure supplement 5
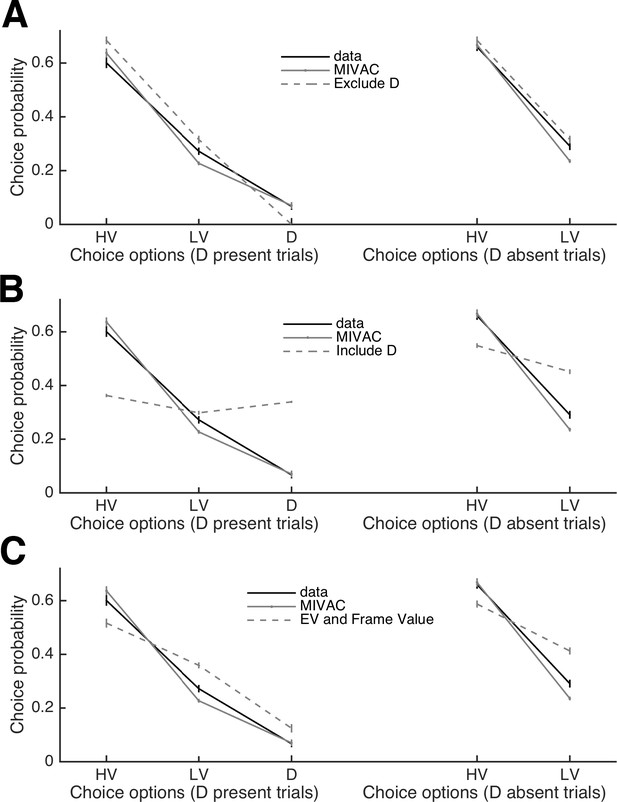
Comparison of MIVAC with multinomial logit (standard economic) choice models.
(A) Comparison of actual choice proportions with the predictions of MIVAC and the logit model that assumes that D cannot be chosen. For obvious reasons, the logit model fails to predict that D is sometimes chosen. (B) The same as in (A) but with the logit model assuming that D is a regular choice option. This logit model predicts too many choices of D. (C) The same as in (A) but with the logit model assuming that choices are based on a combination of the options’ EV and the subjective value of the frame that indicates whether an option is a target or a distractor. This model predicts a too low relative choice accuracy. This is because the model has to assume a very high value difference between target and distractor frames to be able to predict that D is chosen in only a minority of trials (it still tends to predict too many choices of D). As a consequence, the EV difference between HV and LV is marginalized, because both options receive the very high ‘target frame’ value. .
Additional files
-
Supplementary file 1
Tables for statistical results and model parameters
- https://doi.org/10.7554/eLife.39659.023
-
Transparent reporting form
- https://doi.org/10.7554/eLife.39659.024
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Value-based attentional capture affects multi-alternative decision making
eLife 7:e39659.
https://doi.org/10.7554/eLife.39659
