Computational mechanisms of curiosity and goal-directed exploration
- University College London, United Kingdom
- University of Salzburg, Austria
- Christian-Doppler-Klinik, Paracelsus Medical University Salzburg, Austria
- University of Oxford, United Kingdom
- Medical University Vienna, Austria
- Mortimer B. Zuckerman Mind Brain and Behavior Institute, United States
- Max Planck University College London Centre for Computational Psychiatry and Ageing Research, United Kingdom
- University of East Anglia, United Kingdom
Figures
Figure 1
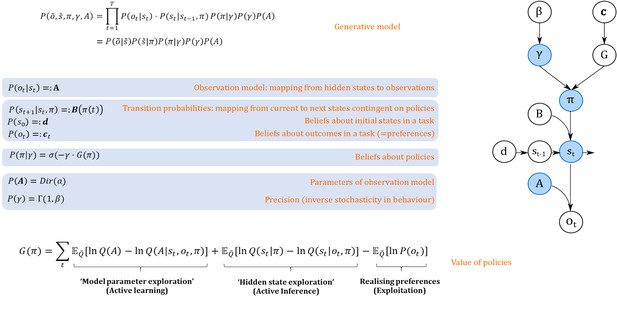
Generative model.
A generative model specifies the joint probability of observations and their hidden causes. The model is expressed in terms of an observation model (likelihood function, that is the probability of observations given true states) and priors over causes. Here, this likelihood is specified by a matrix (A) whose rows are the probability of an outcome under all possible hidden states, . The (empirical) priors in this model pertain to transitions among hidden states (B) that depend upon policies (i.e. sequences of actions), and beliefs about policies contingent on an agent’s precision or inverse randomness, , as well as (full) priors on precision (specified by a Gamma distribution) and an agent’s observation model (specified by a Dirichlet distribution). The key aspect of this generative model is that policies are more probable a priori if they minimise the (sum or path integral of) expected free energy . This implies that policies become valuable if they maximise information gain by learning about model parameters (first term) or hidden states (second term) and realise an agent’s preferences. Approximate inference on the hidden causes (i.e. the current state, policy, precision and observation model) proceeds using variational Bayes (see Materials and methods). Right side depicts the dependency graph of the generative model, with blue circles denoting hidden causes that can be inferred. =Softmax function, Dir = Dirichlet distribution, = Gamma distribution, Q = (approximate) posterior. See Materials and methods for details.
Figure 2
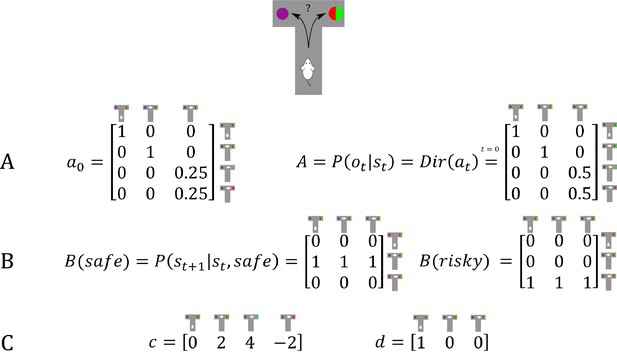
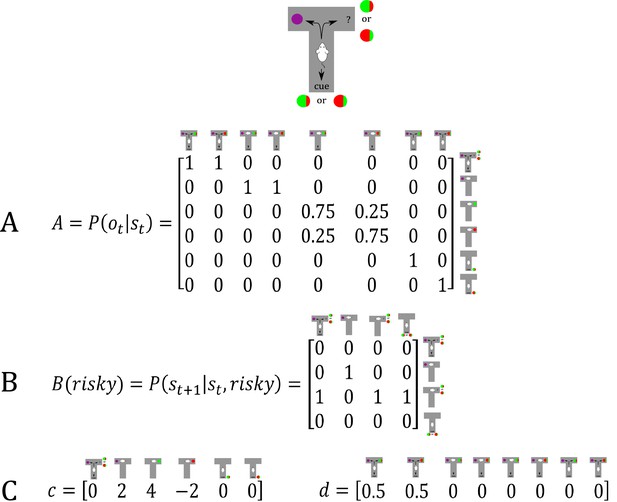
Generative Model of a T-maze task, in which an agent (e.g. a rat) has to choose between a safe option (left arm) and an ambiguous risky option (right arm).
There are three different states in this task reflecting the rat’s location in the maze; namely, being located at the starting position or sampling the safe or risky arm. Further, there are four possible observations, namely being located at the starting position, obtaining a small reward in the safe option, obtaining a high reward in the risky option and obtaining no reward in the risky option. (A) The A-matrix (observation or emission model) maps from hidden states (columns) to observable outcome states (rows, resulting in a 4x3 matrix). There is a deterministic mapping when the agent is in the starting position or samples the safe reward. When the agent samples the risky option, there is a probabilistic mapping to receiving a high reward or no reward. The A-matrix depends on concentration parameters that are updated due to observing transitions between states and observations (in this example: receiving a high or no reward in the risky option), where reflects the prior concentration parameters without having made any observation yet (prior to normalisation over columns). (B) The B-matrix encodes the transition probabilities, that is the mapping from the current hidden state (columns) to the next hidden state (rows) contingent on the action taken by the agent. Thus, one needs as many B-matrices as there are different policies available to the agent (shown here: choose safe or choose risky). Here, the action simply changes the location of the agent. (C) The c-vector specifies the preferences over outcome states. In this example, the agent prefers (expects) to end up in a reward state and dislikes to end up in a no reward state, whereas it is somewhat indifferent about the ‘intermediate’ states. Note that these preferences are represented as log-probabilities (to which a softmax function is applied). For example, these preferences imply that visiting the high reward state is times more likely than the starting point () at the end of a trial. The d-vector specifies beliefs about the initial state of a trial. Here, the agent knows that its initial state is the starting point of the maze.
Figure 3
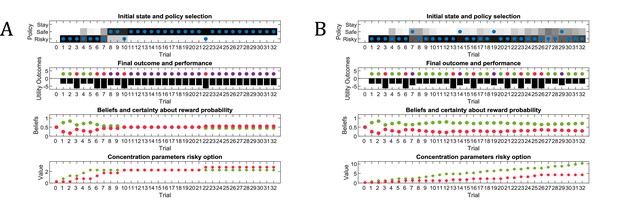
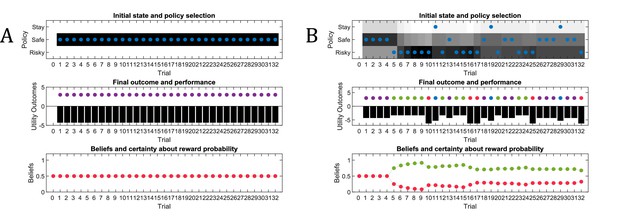
Simulated responses during active learning.
This figure illustrates responses and belief updates during a simulated experiment with 32 trials. The first panel illustrates whether the agent sampled the safe or risky option as indicated by the blue dots, as well as the agent’s beliefs about which action to select. Darker background implies higher certainty about selecting a particular action. The second panel illustrates the outcomes at each trial and the utility of each outcome. Outcomes are represented as coloured dots, where purple refers to a small and safe reward, green to a high reward and red to no reward in the risky option. Black bars reflect the utilities of the outcome. Note that these utilities are defined as log-probabilities over outcomes (see main text and Figure 2), thus a value closer to zero reflects higher utility of an outcome. The third panel illustrates the evolution of beliefs about the reward probabilities in the risky option (red = belief about no reward, green = belief about high reward). The fourth panel illustrates the evolution of the corresponding concentration parameters of the observation model over time (red = concentration parameter for the mapping from risky option to no reward, green = concentration parameter for the mapping from risky option to high reward, cf. Figure 2A). (A) In this example, the simulated agent makes predominantly curious and novelty-seeking choices in the beginning of the experiment. After the tenth trial, the agent is confident that the risky option provides a probability of 0.5 for receiving a high reward, which compels it to choose the safe option afterwards. (B) Same setup as in (A), but now the true reward probability of the risky option is set to 0.75. After sampling the risky option in the beginning of the experiment and learning about the high reward probability of that option, the agent becomes increasingly certain that the risky option has a high probability of a reward. This compels the agent to continue sampling the risky option and only rarely visiting the safe option with low certainty, as illustrated in panel one.
Figure 4
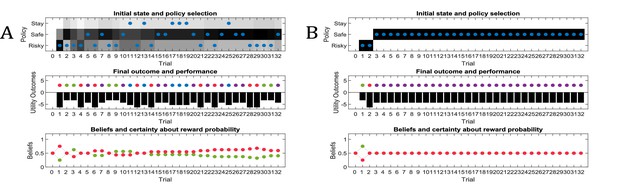
Effects of precision on behaviour.
Same setup as in Figure 3, but now with varying levels of stochasticity. (A) A high degree of random exploration results from very imprecise behaviour (), whereas (B) highly precise behaviour () results in very low randomness in behaviour.
Figure 5
‘Broken’ active learning (parameter exploration).
Same setup as in Figure 3, but now with a true reward probability of 0.75 and no active learning as a determinant of the value of policies (first term of Equation 7, Materials and methods section). (A) If behaviour is very precise (), the agent will never find out that the risky option is more preferable than the safe option, because there is no active sampling of its environment. (B) In contrast, if the agent’s behaviour has a higher degree of randomness (low precision, ), then it will eventually learn about the reward statistics in the risky option from randomly sampling this alternative, and infer that it is preferable over the safe option.
Figure 6
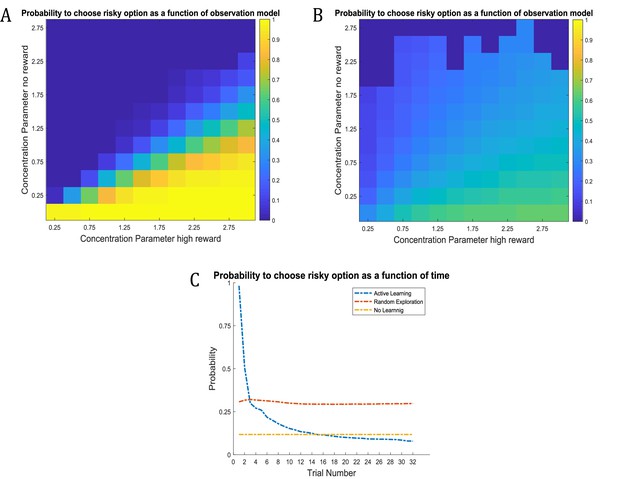
Time-course of active learning and random exploration.
Simulations of 1000 experiments with 32 trials each under a true reward probability of 0.5. (A) Probability to choose the risky option as a function of the concentration parameters for high reward and no reward in the risky option under active learning. The probability to choose the risky (uncertain) option is high if there is high uncertainty about this option at the beginning of a task. Note how the probability of choosing the risky option decreases as the agent becomes more certain that the true reward probability of the risky option is 0.5 (gradient along the diagonal). (B) When there is no active learning but high randomness (low prior precision, ), there is no uncertainty-bonus for the risky option if the agent is uncertain about the reward mapping (lower left corner). The probability to sample the risky option increases only gradually with increasing certainty about a high reward probability (gradient along x-axis). (C) Average probability to choose the risky option as a function of time for active learning (as in A), random exploration (as in B) and in the absence of any learning. Active learning induces a clear preference for sampling the informative (risky) option at early trials. In contrast, random exploration without active learning does not induce a preference for uncertainty-reduction at early trials, and the probability to choose the risky option quickly converges as the estimate of the true reward probability converges to 0.5 due to random sampling of the risky option. In the absence of any learning, the probability to choose the risky option is constant and reflects the precision or randomness in an agent’s generative model (simulated with, ).
Figure 7
Generative model of a T-maze task, in which an agent (e.g. a rat) has to choose between a safe option (left arm) and a risky option (right arm).
In contrast to the previous task, the rat can now be in two different contexts that define the reward probability of the risky option, which can be high (75%) or low (25%). Besides sampling the safe or risky option, it can now also sample a cue that signifies the current context. This results in a state space of eight possible states, defined by the factors location (starting point, cue location, safe option, risky option) and context (high or low reward probability in risky option). Further, there are seven possible observations the agent could make, namely being at the starting position, sampling the safe option, obtaining a/no reward in the risky option, and sampling the cue that indicates a high/low reward probability. (A) The A-matrix (observation or emission model) maps from hidden states (columns) to observable outcome states (rows, resulting in an 8 × 7 matrix). There is a deterministic mapping when the agent is in the starting position, samples the safe reward or samples the cue. When the agent samples the risky option, there is a probabilistic mapping to receiving a high reward or no reward that depends on the current context. In contrast to the previous example, no updates of the A-matrix take place in this task. (B) The B-matrix encodes the transition probabilities, that is the mapping from the current hidden state (columns) to the next hidden state (rows) contingent on the action taken by the agent, which simply changes the location of the agent. For simplicity, only the transition probabilities for the factor location are shown, which replicate across the two contexts (resulting in an 8 × 8 transition matrix). (C) The c-vector specifies the preferences over outcome states. In this example, the agent prefers (expects) to end up in a reward state and dislikes to end up in a no reward state, whereas it is indifferent about the ‘intermediate’ states (starting position or cue location). The d-vector specifies beliefs about the initial state of a trial. Here, the agent knows that its initial state is the starting point of the maze, but has a uniform prior over the two contexts. In experiments where the context is stable, this uniform prior can be updated to reflect experience-dependent expectations about the current context.
Figure 8
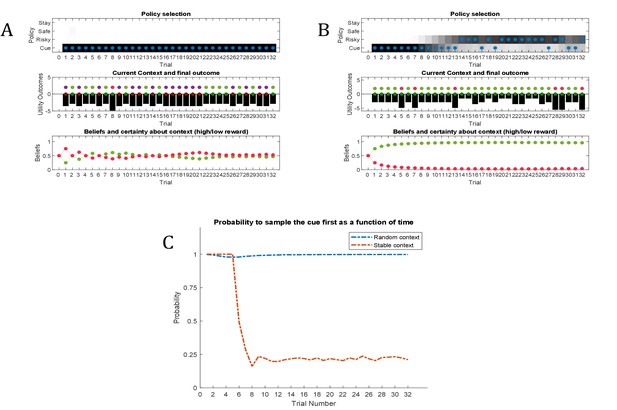
Simulated responses during inference.
In this experiment, the current context indicates either a high (75%) or low (25%) reward probability in the risky option. The agent can gain information about the current context of a trial by sampling a cue, which signifies the current context. (A) Simulated experiment with 32 trials and a random context that changes on a trial-by-trial basis: the first panel illustrates the choice of the agent at the beginning of a trial and the agent’s beliefs about action selection (darker means more likely). Note that the agent always chooses to sample the cue first before choosing the safe or risky option. The second panel illustrates the outcomes of every trial (purple = safe option, green = high reward in risky option, red = no reward in risky option) and their utilities (black bars, closer to zero indicates higher utility). Note that a green or red outcome indicates that the agent has chosen the risky option after sampling the cue. Dark red and green dots indicate the current context as signified by the cue (dark red = low reward probability in risky option, dark green = high reward probability in risky option). Note that the agent only samples the risky option if the cue indicates a high reward context. The third panel shows the evolution of beliefs concerning the current state (i.e. high or low reward context). (B) Same setup as before, but now with a constant context that indicates a high reward probability in the risky option. Here, the agent becomes increasingly confident that it is in a high reward context, which compels it to sample the risky option directly after about one third of the experiment, whilst gathering information in the cue location in the first third of the experiment. (C) Time-course of the probability to sample the cue first as a function of trial number in an experiment (in 1000 simulated experiments). If the context is random, there is a nearly 100% probability to sample the cue first at every trial. In a stable context, the probability to sample the cue shows a sharp decrease once the agent has gathered enough information about the current (hidden) state.
Figure 9
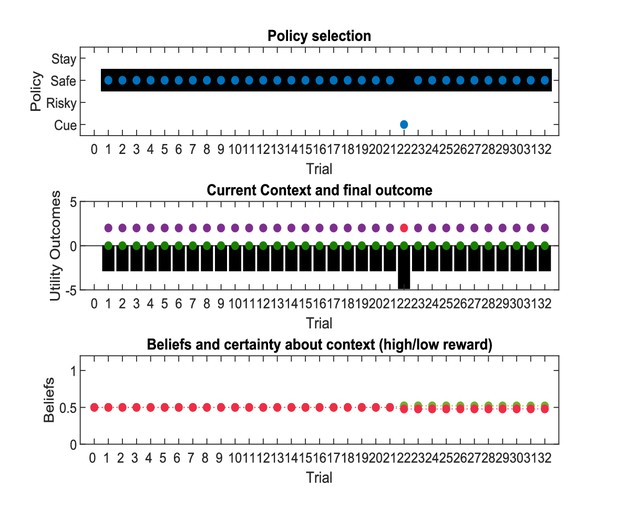
‘Broken’ active inference.
Same setup as in Figure 8, but now without a ‘hidden state exploration’ bias in policy selection (second term of Equation 7, Materials and methods section). The agent fails to learn that there is a constant high reward probability for the risky option because it does not gain information about the current hidden state (context). Consequently, it continues to prefer the safe option. The probabilities to sample different options (first panel) now simply reflect the agent’s prior preferences as encoded in the c-vector (cf., Figure 7).
Figure 10
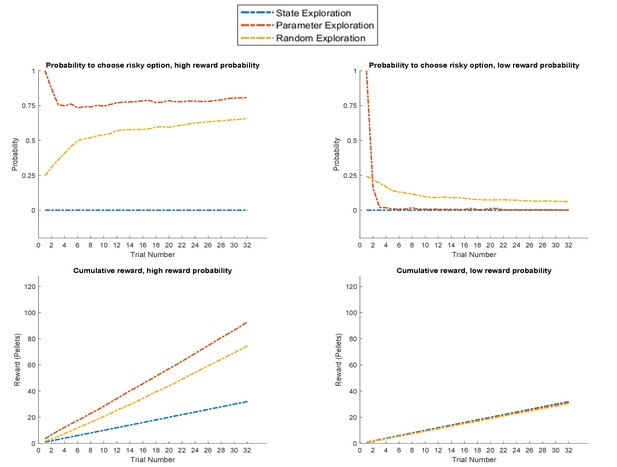
Response profiles of a ‘state exploration’, ‘parameter exploration’ and ‘random exploration’ agent in a task that requires learning.
In the task described at the top of Figure 2, only the ‘parameter exploration’ agent (no state exploration) flexibly adapts to the current reward statistics, whilst the ‘state exploration’ (no parameter learning) agent fails to form a representation of the task statistics. Upper panel: probability for each of the three agents to choose the risky option if it is associated with a high (left, 85%) or low (right, 15%) reward probability. Lower panel: average cumulative reward (measured in pellets, where low reward = one pellet and high reward = four pellets) in 100 simulated experiments in a high (left) and low (right) reward probability setting, indicating an advantage for the ‘parameter exploration’ agent when the risky option is associated with a high reward probability.
Figure 11
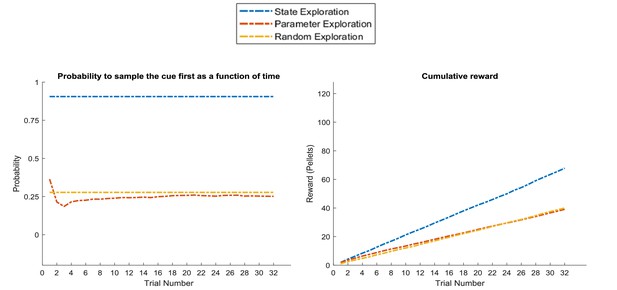
Response profiles of a ‘state exploration’, ‘parameter exploration’ and ‘random exploration’ agent in a task that requires inference.
In the problem introduced in Figure 7, where an agent can infer the randomly changing context from a cue, ‘parameter exploration’ will be ineffective, because there is no insight that could be transferred from one trial to the next. ‘State exploration’, in contrast, provides an effective solution to this task, because it allows an agent to infer the current context on a trial-by-trial basis. Left panel: probability to choose the informative cue at the beginning of a trial. This shows that only the ‘state exploration’ agent correctly infers that it has to sample the cue at the beginning of every trial to adjust its behaviour to the current context (defined as a high or low reward probability in the risky option). Consequently, it outperforms the ‘parameter exploration’ and ‘random exploration’ agent in its cumulative earnings in this task (right panel).
Figure 12
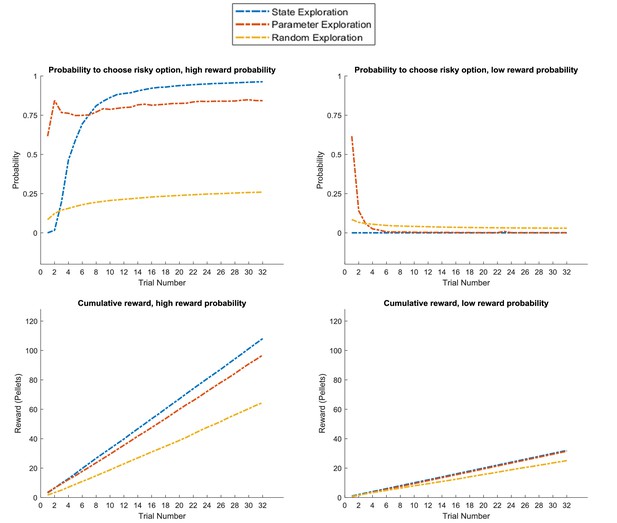
Response profiles of a ‘state exploration’, ‘parameter exploration’ and ‘random exploration’ agent in a task that requires learning or inference.
Same problem as in Figure 11, but now with a stable high or low reward context (as in Figure 8B). This task can be solved by either sampling the risky option to learn about its reward statistics (‘parameter exploration’), or sampling the cue to learn about the current context and adjusting the prior over contexts due to constant feedback from the cue (‘state estimation’). This can be seen in the response profiles in the upper panel, such that the ‘parameter exploration’ agent has a strong preference for sampling the uncertain risky option in the beginning of the trial (left and right), while the ‘state exploration’ agent only starts sampling the risky option at the beginning of the trial if it has sampled the cue several times before, which always indicates a high reward context (left, cf. Figure 8). This leads to a similar performance level of these two agents as measured by the cumulative reward, which exceeds the performance of the ‘random exploration’ agent (lower panel).
Figure 13
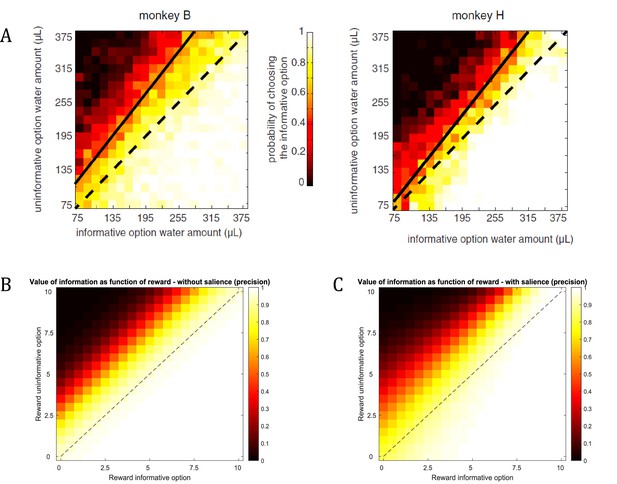
Dynamic relationship between reward and information.
(A) Empirical findings from Blanchard et al., 2015 suggest a modulatory effect of reward on the value of information. The higher the expected reward of the options, the more do monkeys prefer the option with the additional information about the reward identity during the delay period. For example, the preference for the informative option will be stronger if both options offer 315μL of water compared to both options offering 75μL of water. (B) Assuming a constant salience of different offer amounts (i.e. a constant precision of policy selection), active learning (and inference) predicts a preference for the informative option that is constant across different reward amounts (simulated from 0 to 10 pellets). That means that the preference for the informative option is the same when both options offer 1 or 10 pellets, for instance. (C) When taking a dynamic change of the precision of policy selection for different offer amounts into account (ranging parametrically between for zero pellets in both offers and for 10 pellets in both offers), the simulated preferences match the empirical results from Blanchard et al., 2015. This highlights the importance of the interplay between the (extrinsic and intrinsic) values of options in active learning and active inference.
© 2014 Neuron. All rights reserved. Reprinted from Blanchard et al. (2015) with permission from Elsevier. This panel is not available under CC-BY and is exempt from the CC-BY 4.0 license
Appendix 1—figure 1
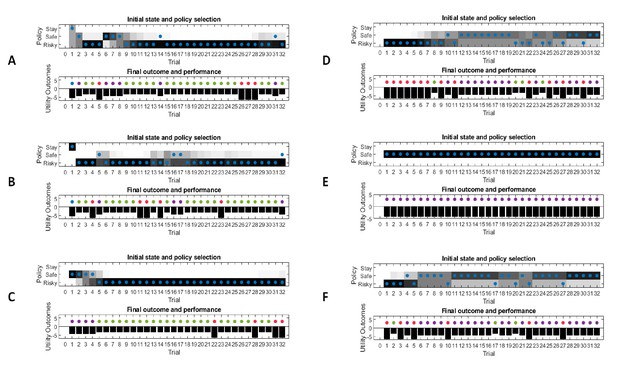
The agent’s prior on the observation model determines the value of information of the risky option.
Same setup as in Figures 3–5, but with different priors over the observation model. (A) Full uncertainty over an agent’s observation model induces the same information value for all three options, whereas uncertainty over the mapping from the starting point or safe option induce a specific epistemic value for these options (B and C). These priors can also induce optimistic (D) or pessimistic (E) behaviour, based on a high (prior) reward expectation in a low reward probability (0.25) task or a low (prior) reward expectation in a high reward task (0.75), respectively. (F) A lower learning rate leads to slower learning about a low reward probability (0.25) in the risky option or, equivalently, to a longer dominance of information-seeking behaviour.
Appendix 1—figure 2
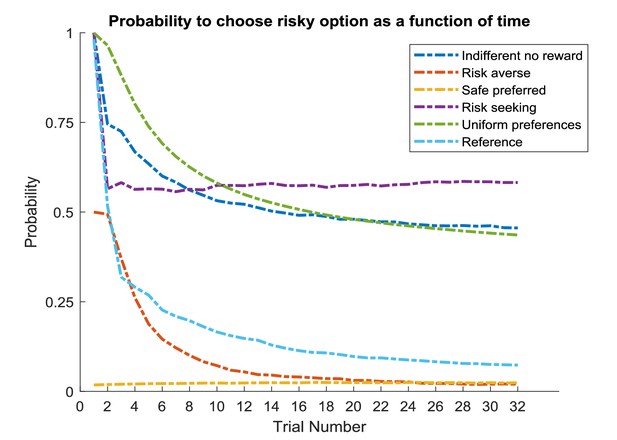
Prior preferences over outcomes determine an agent’s risk preferences.
Same setup as in Figure 6A but with varying preferences over outcomes, compared to the reference specification of c = [0 2 4 –2] in log-space used above (bright blue line), which reflects an agent’s preference for the starting position, the small safe reward, the high reward and no reward, respectively. Dark blue line reflects the same information seeking behaviour in the beginning of an experiment but less risk aversion in later trials by equating an agent’s preference for obtaining no reward to staying in the safe position (c = [0 2 4 0]). Purple line reflects a risk seeking agent (c = [0 2 8 –2]) whereas red line reflects a risk averse agent (c = [0 2 4 –4]). Yellow line reflects an agent that has an equal preference for the high and low reward (c = [0 4 4 –2]), and consequently never chooses the risky option. Green line reflects an agent with flat preferences (c = [0 0 0 0]), which is purely driven by information gain until it converges on a stable probability for choosing the risky option. Time-course averaged over 1000 experiments.
Appendix 1—figure 3
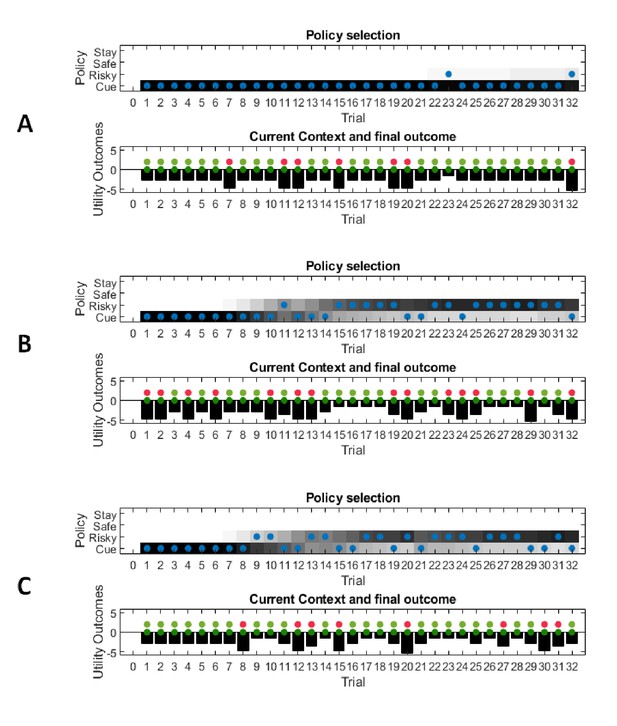
Prior preferences over outcomes determine the cost of sampling information in the active inference task – single experiment simulations.
(A) An agent that prefers sampling the cue will continue to sample the cue at the beginning of a trial, even if its uncertainty about the hidden state has been resolved. (B) An agent with neutral preferences for the cue will switch to sampling the preferred (risky) option immediately once its uncertainty about the (high reward) hidden state is sufficiently resolved (equivalent to Figure 8B). (C) An agent with a negative preference for the cue will try to switch to the preferred option as quickly as possible, but may go back to sample the cue more often because its uncertainty has not been resolved sufficiently.
Appendix 1—figure 4
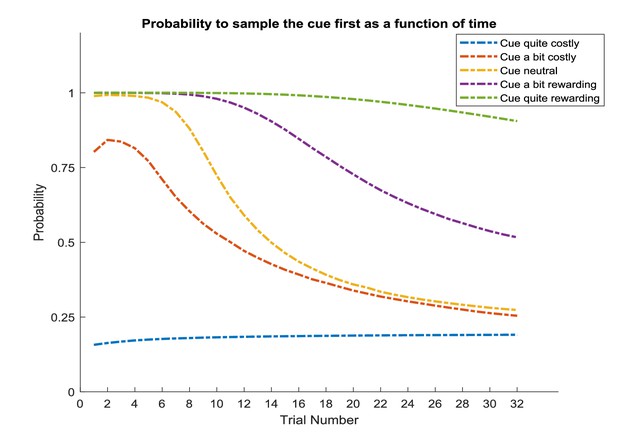
Prior preferences over outcomes determine the cost of information sampling in the active inference task – simulations over multiple experiments – simulations over 1000 experiments..
The yellow line reflects the agent introduced in Figure 8B with neutral preferences for the cue location, specified as c = [0 2 4 –2 0 0], which reflects its preferences for the starting location, safe reward, high reward, no reward and the cue location (signalling a high or low reward state), respectively. Agents with a slight preference for visiting the cue only slowly decrease their preference for sampling the cue at the beginning of a trial (purple: c = [0 2 4 –2 0.25 0.25]; green: c = [0 2 4 –2 0.5 0.5]). Agents with a negative preference for the cue location move away from sampling the cue quicker (red: c = [0 2 4 –2 −0.25 –0.25]; blue: c = [0 2 4 –2 −0.5 –0.5]). Time-course averaged over 1000 experiments.
Appendix 1—figure 5
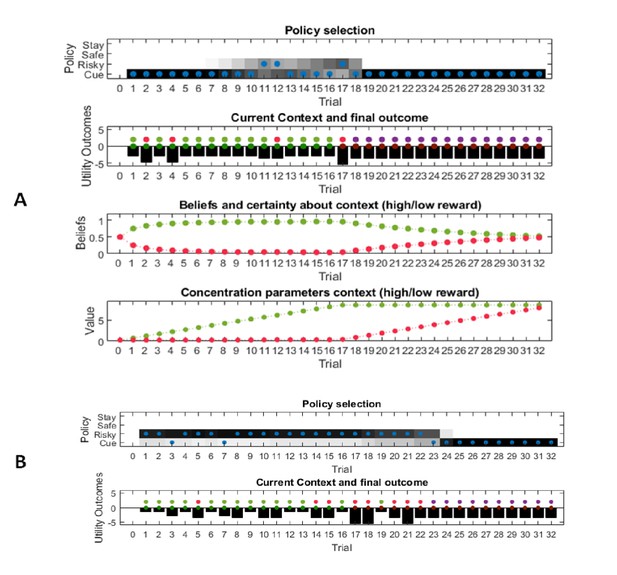
An active inference agent correctly infers a change in the environment – single experiment simulations.
(A) An active inference agent correctly learns that it starts in a high reward environment, and slowly begins to sample the risky option at the beginning of a trial once it has inferred a high reward context. After a switch of context to a low reward environment in trial 16, however, the agent starts sampling the cue again. This is induced by a negative outcome at trial 17 and then further reinforced by a different context signalled by the cue. Thus, the active inference agent correctly infers when to start sampling information again as a function of its uncertainty about the world. (B) If an agent has optimistic prior expectations about being in a high reward context, it starts sampling the risky option immediately even at the beginning of the experiment, and it will take the agent longer to infer a switch of context in the second half of the experiment.
Appendix 1—figure 6
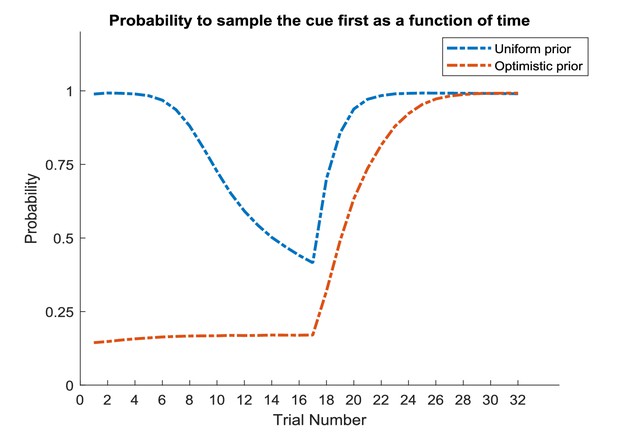
An active inference agent correctly infers a change in the environment – simulations over multiple experiments.
Same agents as in Appendix 1—figure 5 (A and B) simulated over 1000 experiments. The neutral active inference agent correctly infers a switch after the first half of the experiment and starts sampling the cue again. The optimistic active inference agent does not sample the cue in the first half of the experiment, but starts visiting the cue location once it has inferred that the context has changed.
Appendix 2—figure 1
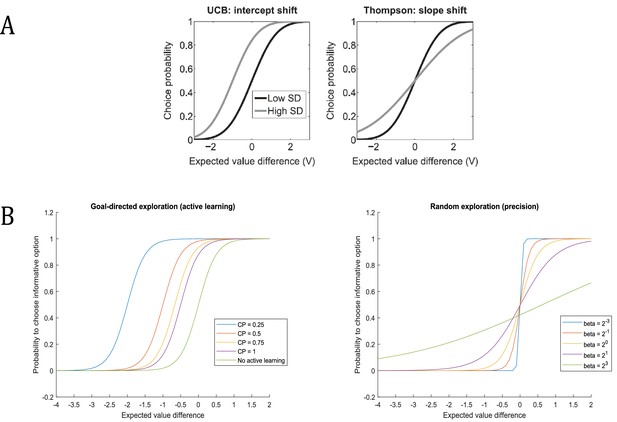
Effects of different algorithms for exploration on choice probabilities.
(A) Left panel: Algorithms based on an uncertainty bonus, such as UCB, change the intercept in the probability for choosing the uncertain option, plotted as a function of the difference in expected value between the uncertain option and an alternative option. Right panel: Algorithms based on randomness, such as Thompson sampling, change the slope of the choice probability, where an increase in randomness decreases the steepness of the choice curve. Reproduced from (Gershman, 2018a) (B) Left panel: ‘model parameter exploration’ in active inference acts as an uncertainty bonus and, analogously to UCB, changes the intercept of the probability to sample an uncertain option as a function of the prior uncertainty over this option. Different lines reflect different concentration parameters for the mapping to high or no reward in the risky option (cf., Figure 2, CP = concentration parameter). ‘Hidden state exploration’ in active inference has analogous effects. Right panel: prior precision of policy selection () affects the randomness of choice behaviour, and consequently the slope of the choice function.
© 2017 Cognition. All rights reserved. Reprinted from Gershman (2018a) with permission from Elsevier. This panel is not available under CC-BY and is exempt from the CC-BY 4.0 license.
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.41703.015
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Computational mechanisms of curiosity and goal-directed exploration
eLife 8:e41703.
https://doi.org/10.7554/eLife.41703
