Can Hamilton’s rule be violated?
- University of Amsterdam, The Netherlands
Figures
Figure 1
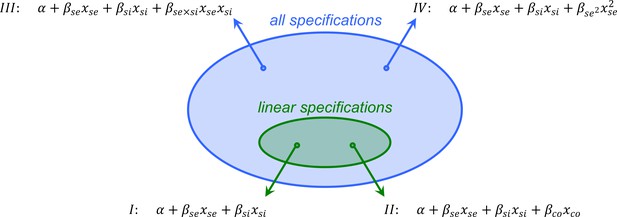
The value of coefficients and may depend on the specification chosen.
If is included (as in specification II), these values will be different from when is not included (specification I). Including an interaction term (III) or a quadratic term (IV) will also make …
Figure 2
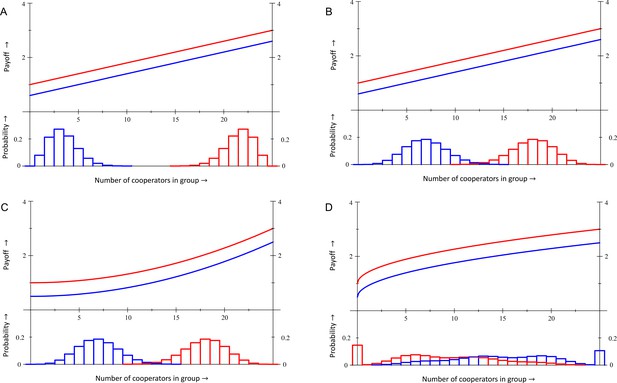
Within each panel, the fitness functions are depicted in the upper part.
In panels A, B and C the bottom part depicts population structure profiles of mutant co-operators at (blue) and of mutant defectors at (red). In panel D the bottom part depicts the …
Figure 3
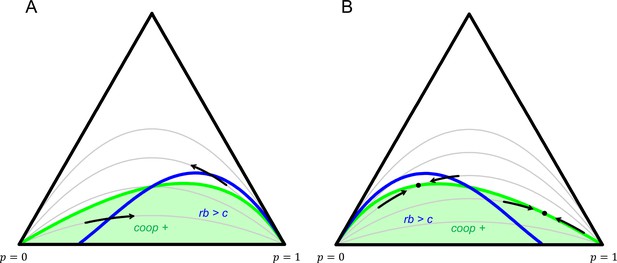
Dynamics for two 2-player games.
Every point in the simplex represents a population state . The left down corner is , which has only groups with co-operators; the right down corner is , which has only groups with …
Figure 4
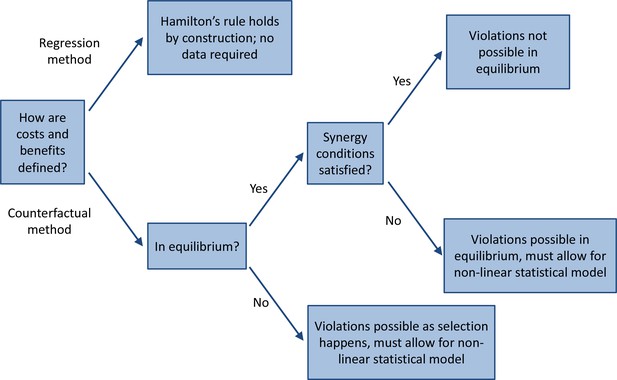
A road map for empirical tests of Hamilton’s rule.
The three synergy conditions are that for all , that for all , and that increases with .
Appendix 1—figure 1
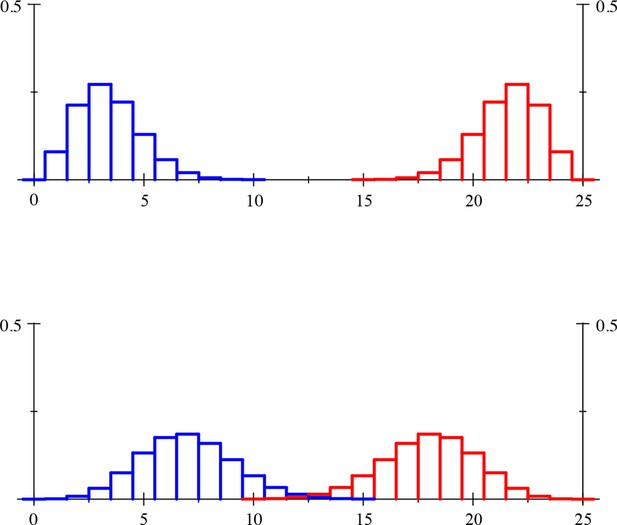
Population structure profiles (blue) for co-operator invaders at , and (red) for defector invaders at .
Defectors at only find themselves in groups with defectors, co-operators at only find themselves in groups with co-operators (not depicted in the figures). In the lower panel mutants …
Appendix 1—figure 2
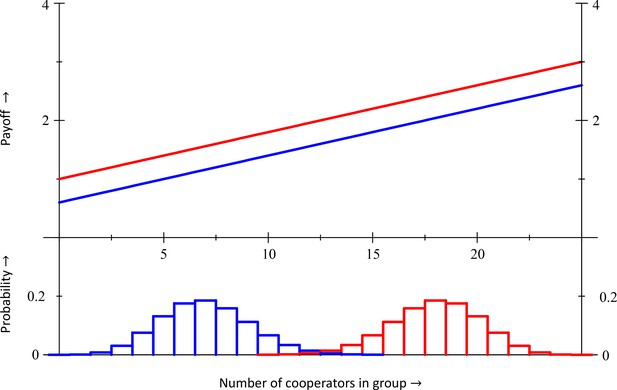
The population structure profiles are depicted in the lower half of the figure, the payoffs in the upper half.
https://doi.org/10.7554/eLife.41901.009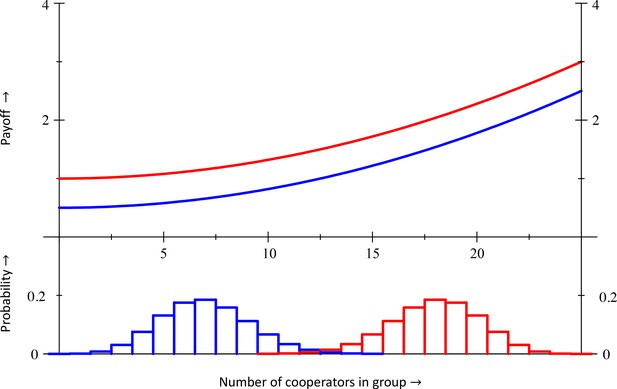
Appendix 1—figure 3
The population structure profiles are depicted in the lower half of the figure, the payoffs in the upper half.
https://doi.org/10.7554/eLife.41901.010
Appendix 1—figure 4
The population structure profiles are depicted in the lower half of the figure, the payoffs in the upper half.
https://doi.org/10.7554/eLife.41901.011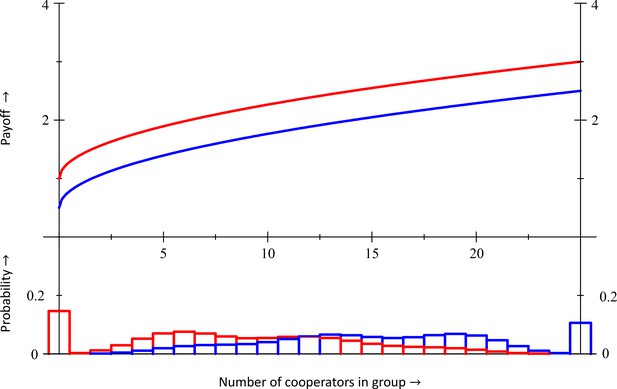
Appendix 1—figure 5
The previous figures depicted , which is the population structure profile at , and , which is the population structure profile at .
The payoffs co-operators get, when they find themselves in groups according to would be compared to the payoffs defectors get when they are in a group of defectors only in order to determine …
Appendix 1—figure 6
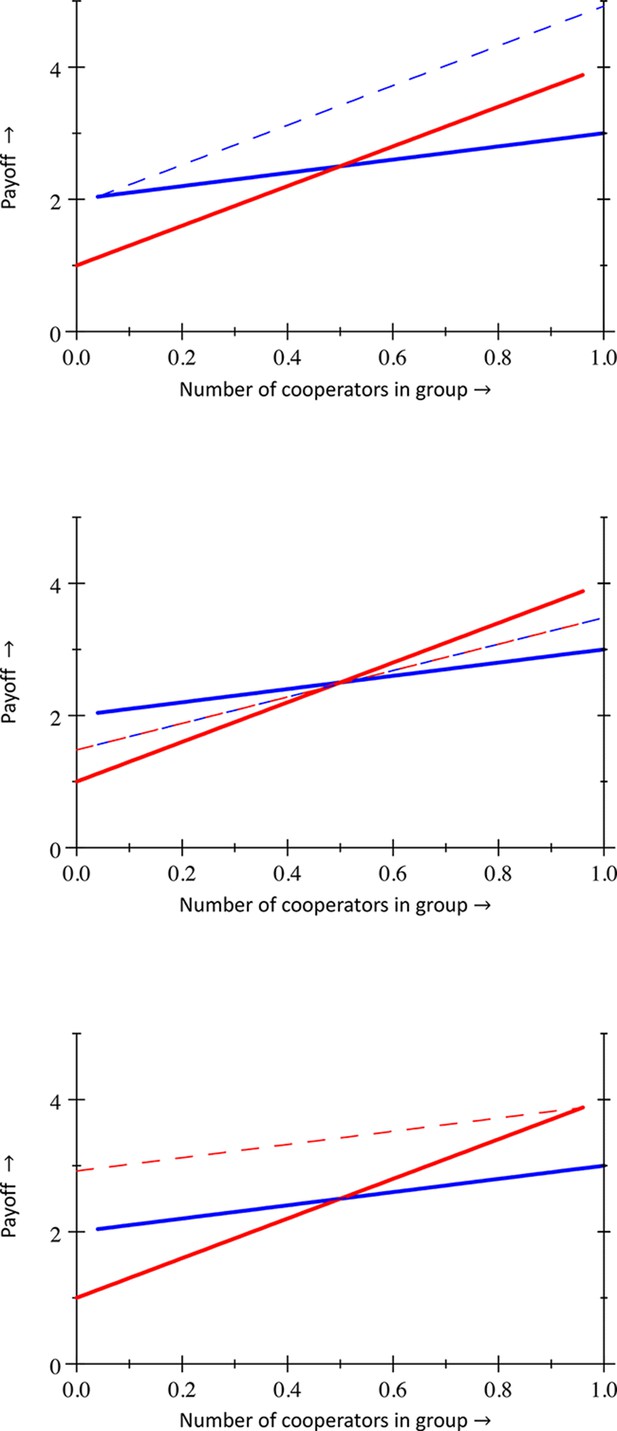
The according to the regression method coincides the true at (top panel, red), but the according to the regression method (dotted blue) differs from the true (solid blue).
The and according to the regression method coincide with each other at (middle panel, dotted lines) but do not coincide with the true (solid red) and (solid blue). The according to …
Appendix 1—figure 7
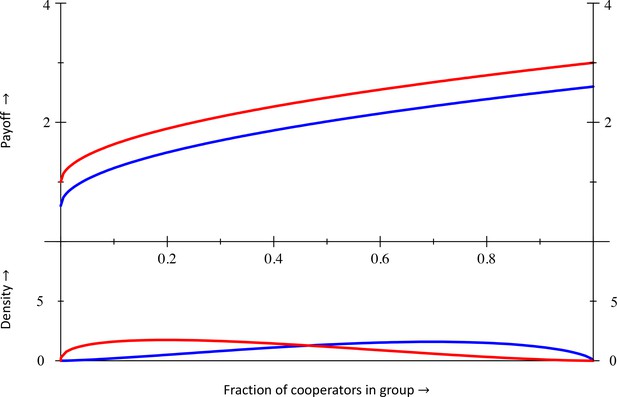
With parameters , and , the equilibrium frequency of co-operators, at which , is .
Inclusive fitness there is . Section X specifies the for this example.
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.41901.006
