A primal role for the vestibular sense in the development of coordinated locomotion
- New York University School of Medicine, United States
Figures
Figure 1 with 3 supplements
Larvae climb using bodies and pectoral fins.
(A) Schematic of hydrostatic climbing mechanics. Like a rocket, a larva generates thrust in the direction it points (top), enabling it to generate upwards trajectories by rotating upwards to adopt nose-up postures. Complementarily, it may generate lift like a helicopter (bottom), creating an attack angle between trajectory and posture. (B) Trajectory of individual swim bouts as a function of posture, for control (2912 bouts) and finless larvae (1890 bouts). The unity line corresponds to 0 attack angle. Example postures and corresponding trajectories (inset) are indicated with red circles. (C) Representative epochs of climbing by one control and one finless larva, depicting posture and trajectory at the times of sequential bouts. Relative positions are to scale, but the body schematic is smaller than actual size to better highlight the trajectory. (D) Mean attack angles for control and finless siblings from six clutches (pairwise t-test, , ). (E) Cumulative fractions of postures during climbs with trajectories greater than 20°, for control and finless siblings, plotted as mean ± S.D. across clutches. (F) Absolute deviation of posture from horizontal during climbs in (D) for control and finless siblings (, ).
Figure 1—figure supplement 1
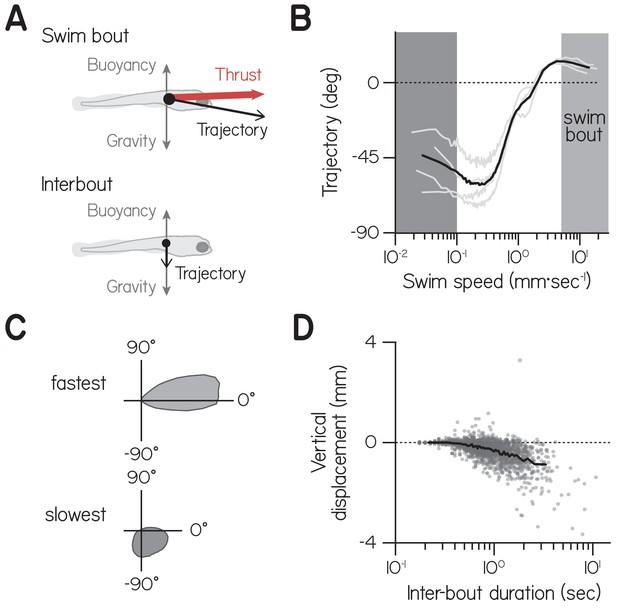
Larvae tend to sink between bouts.
(A) Schematic of hydrostatic forces acting on larvae absent lift during bouts (top) and between bouts (bottom). (B) Trajectory as a function of swim speed, plotted as means of equally-sized bins for four clutches (gray lines) and their mean (black). Swim bouts (light gray band, speeds faster than 5 mm·s−1) tended slightly upwards, while larvae sank at slow speeds, particularly slower than 0.1 mm·s−1 (dark gray band). (C) Polar probability distributions of trajectories during swim bouts (light gray, top) and at speeds slower than 0.1 mm·s−1 (dark gray, bottom). (D) Vertical displacement during the interval between two bouts (when speed decreased below 5mm·s−1) as a function of interval duration, for individual bouts and mean of equally-sized bins.
Figure 1—figure supplement 2
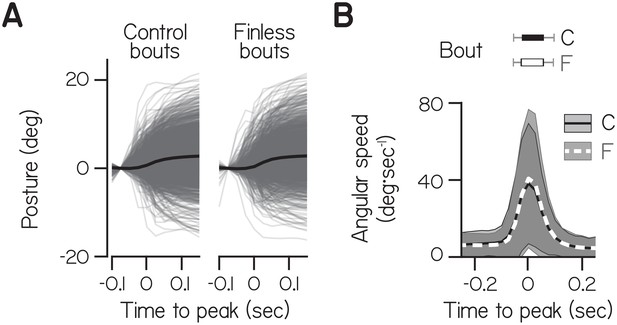
Posture as a function of time during bouts by control and finless siblings.
Data from individual bouts (gray lines) and their mean (black) were aligned to peak speed at time 0 and baseline subtracted at −0.75 s. (B) Angular speed as a function of time during bouts (bottom), plotted as mean and S.D., for control and finless siblings. Durations when speed exceeded 5 mm·s−1 are plotted for control and finless larvae (top) as median and 95% confidence interval.
Figure 1—figure supplement 3
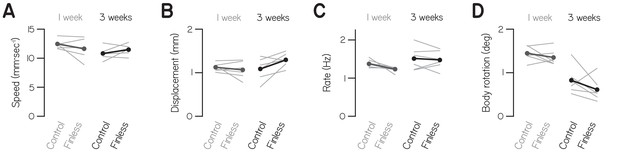
Basic swimming statistics are unaffected by fin amputation at 1 and 3 wpf.
(A–D) Mean maximum speed across bouts (A), mean net displacement (B), mean rate (C), and mean absolute body rotation (D) of swim bouts are plotted as thin lines by clutch (n = 6, eight larvae per) for larvae with amputated fins and unaltered siblings at 1 and 3 wpf. Within group means are plotted as thick lines and points.
Figure 2 with 2 supplements
Development of fin-body coordination.
(A) Schematic of fin-body coordination for climbing. Positive posture changes are paired with positive attack angles and negative body rotations with no attack angle, reflecting exclusion of the fins. (B) Mean linear and angular acceleration during swim bouts at 1, 2, and 3 weeks post-fertilization (wpf), temporally aligned to peak linear speed (time 0). The window used to compute posture change is highlighted in gray. (C) Attack angle as a function of posture change for bouts at 1, 2, and 3 wpf, with cropped attack angle probability distributions (right). Data plotted as means of equally sized bins (black lines) and superimposed with best-fit sigmoids and their bootstrapped S.D. (D) Fin-body ratio, defined as the maximal slope of best-fit sigmoid to attack angle and posture change, is plotted with 95% confidence intervals as a function of age. (E,F) Mean attack angle (E) and absolute deviation from horizontal (F) for each clutch and age, evaluated over 48 hr, are plotted as functions of fin-body ratio with Pearson’s correlation coefficients (; p=5.6E-6 for attack angle and p=6.3E-3 for deviation from horizontal). Small values convey body-dominant synergies, while large values convey fin-dominant synergies. Developmental trajectories for the four individual clutches are plotted on identical axes (right).
Figure 2—figure supplement 1
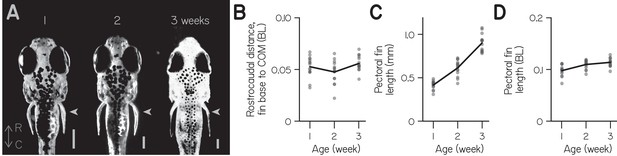
Pectoral fins and bodies grow proportionally.
(A) Grayscale, dorsal-perspective photomicrographs of representative larvae at 1, 2, and 3 wpf, with rostrocaudal axis labeled (R–C). Pectoral fins are indicated with arrowhead. Gamma was adjusted and images scaled to comparable head length (scale bars 0.25 mm). (B) Rostrocaudal distance from base of the pectoral fins to the estimated center of mass (COM, see Materials and methods), in body lengths (BL), as a function of age (n = 15 larvae). (C) Pectoral fin length as a function of age. (D) Pectoral fin length normalized to body length as a function of age.
Figure 2—figure supplement 2
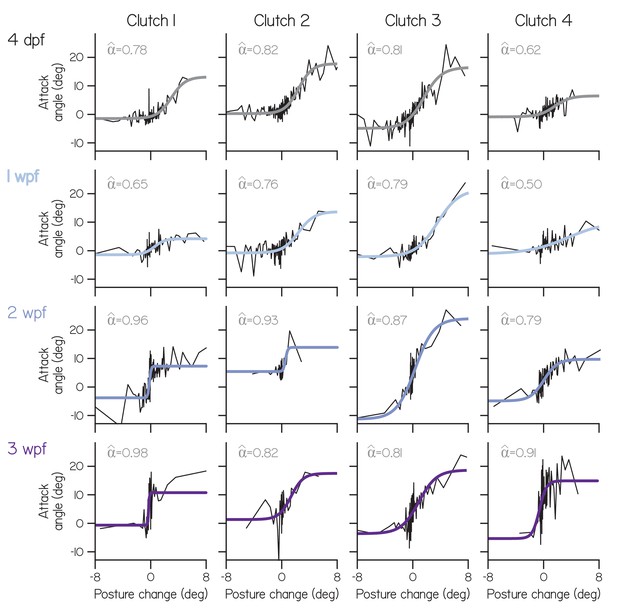
Clutch- and age-specific fin bias.
Attack angle as a function of posture change for individual clutches (columns) at each age (rows), plotted as means of equally-sized bins, superimposed with four parameter sigmoid fits. Empirical fin bias (), computed as an index of maximal sigmoid slope (slope/(1+slope)), is listed.
Figure 3
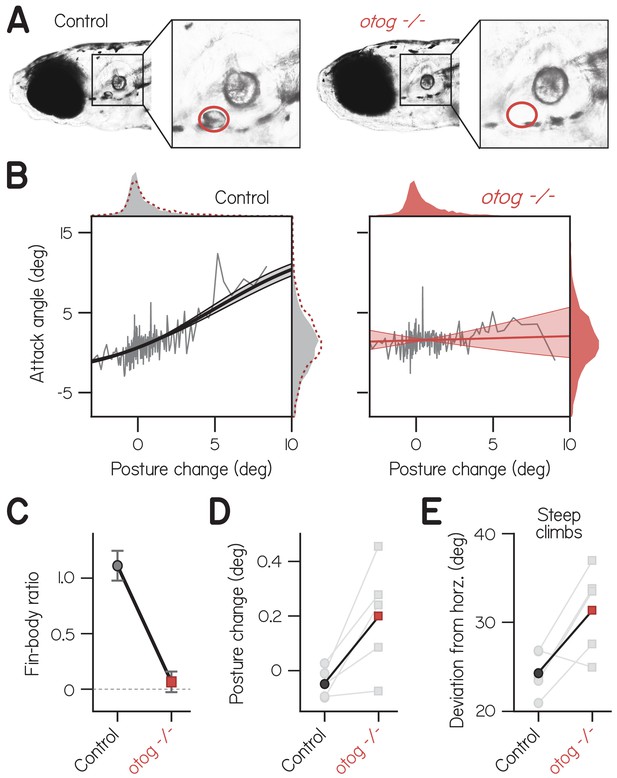
Fin-body coordination is abolished by peripheral vestibular lesion.
(A) Representative lateral photomicrographs, one of a larva with typical development of utricular (anterior) otoliths (top, control: wild-type or heterozygous for otogelin) and another of its sibling lacking utricular otoliths (bottom, otogelin -/-). Utricle position is encircled in red. (B) Attack angle as a function of posture change for bouts by control larvae (4767 bouts) and otogelin -/- siblings (3656 bouts). Data plotted as means of equally sized bins (gray lines) superimposed with best-fit sigmoids and their bootstrapped S.D. Marginals show cropped probability distributions, with otogelin -/- marginals superimposed on control data as dashed lines. (C) Fin-body ratio, or the maximal slope of best-fit sigmoid, plotted with 95% confidence interval. (D) Median posture change during bouts by individual clutches (gray) and their means. Pairwise t-test, t4 = 3.13, p = 0.035. (E) Mean deviation of posture from horizontal during steep climbs (> 20°). Pairwise t-test, t4 = 3.02, p = 0.039.
Figure 4
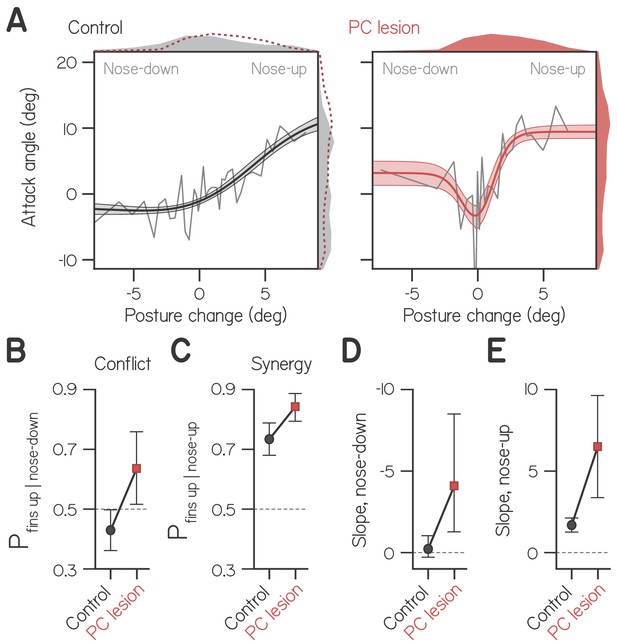
Cerebellar lesion impairs fin-body coordination.
(A) Attack angle as a function of posture change for bouts by control larvae (602 bouts) and siblings with lesioned Purkinje cells (408 bouts). Data plotted as means of equally-sized bins (gray lines) superimposed with best-fit sum of two sigmoids and their bootstrapped S.D. Marginals show cropped probability distributions, with marginals from lesioned larvae superimposed on control data as dashed lines. (B) Proportion of bouts with attack angles more positive than 1 wpf baseline (−1.59°) given nose-down posture change (< −1°), with bootstrapped 95% CI. (C) Proportion of bouts with attack angles more positive than 1 wpf baseline (−1.59°) given nose-up posture change (> 1°), with bootstrapped 95% CI. (D,E) Largest magnitude slopes of the nose-down (D) and nose-up (E) best-fit sigmoids to data in (A), with bootstrapped 95% CI.
Appendix 1—figure 1
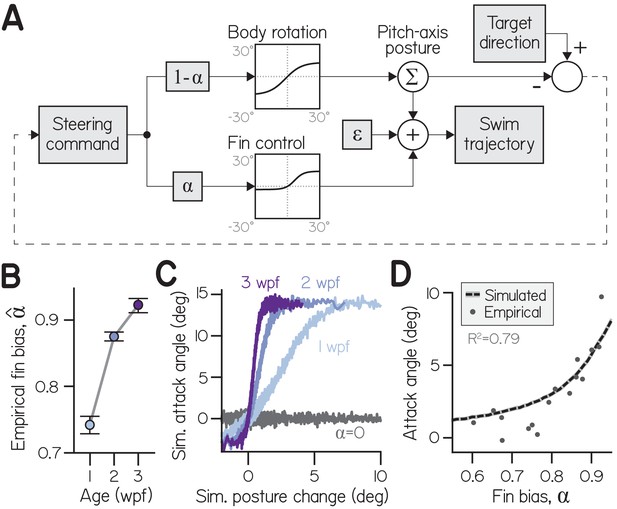
A one-parameter control system captures fin-body coordination in silico.
(A) Circuit diagram to transform pitch-axis steering commands into climbing swims using the body and pectoral fins. Steering commands are defined by the direction of a target in egocentric coordinates. The relative weight of commands to rotate the body (to direct thrust) and produce an attack angle with the fins (by generating lift) is dictated by fin bias (). To model physical transformations from commands into kinematic variables, commands to the body and fins are filtered to impose empirically-derived ceilings and floors on posture changes and attack angles (see Materials and methods). Swim trajectory is defined by posture (fish propel where they point) but modified by attack angle and error (). (B) Empirical fin bias (), computed from maximal sigmoid slope (slope/(1+slope)), as a function of age with 95% confidence intervals. (C) Attack angle as a function of posture change, plotted as means of equally-sized bins. Climbs to 100,000 targets were simulated using empirical fin bias () from 1, 2, and 3 wpf larvae, and at for comparison. (D) Mean attack angle for simulated larvae with parameterized fin bias (line), superimposed on empirical attack angles and fin biases () for each clutch at each age. Simulated attack angles at account for 79% of variation in empirically observed attack angles (R2).
Appendix 1—figure 2
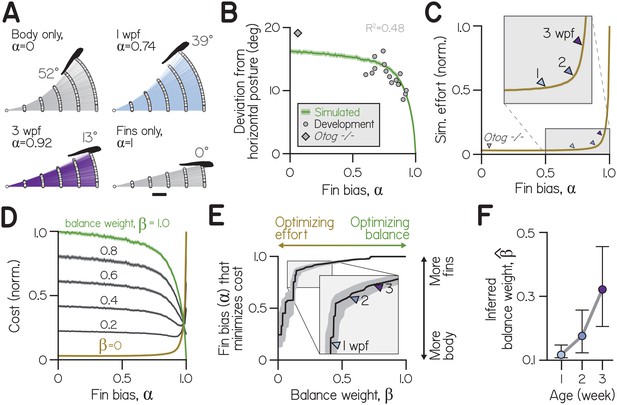
Effects of fin-body coordination on balance-effort trade-off.
(A) Trajectories (lines) and initial positions (dots) of bouts simulated with the control system in (A) at fin biases of 0, 0.74 ( at 1 wpf), 0.92 ( at 3 wpf), and 1.0, for 1000 larvae swimming towards targets 25 μm away. Posture following the fifth bout of the steepest climb is superimposed. Scale bar equals 1 mm. (B) Simulated absolute deviation from horizontal posture as a function of , plotted as mean (green line) and bootstrapped 99% confidence intervals (shaded band). Data are superimposed on empirical values for individual clutches of a given age (circles, Development, R2 = 0.48) and otog-/- larvae (diamond). (C) Effort, the sum of squared motor commands to the body and fins, from simulations in (B) normalized and plotted as a function of as mean (line) and bootstrapped 99% confidence intervals (shaded band). Empirical fin biases at 1, 2, and 3 wpf and for otog-/- larvae are indicated with triangles. (D) Cost as a function of fin bias, computed as sums of normalized curves in (B) and (C) weighted by (balance weight) and (), respectively (left). When (green), cost is equivalent to normalized deviation from horizontal. When (ochre), cost is equivalent to effort. Intermediate cost functions are plotted for increasing by 0.2, with 99% confidence interval (shaded band). (E) Fin bias at which cost was minimized is plotted at each value of balance weight, with 95% confidence intervals. (F) Inferred balance weight () is plotted as a function of age, with 95% confidence intervals. This weight gives the cost function minimized by empirical fin bias at a given age (from the curve in E).
Appendix 1—figure 3
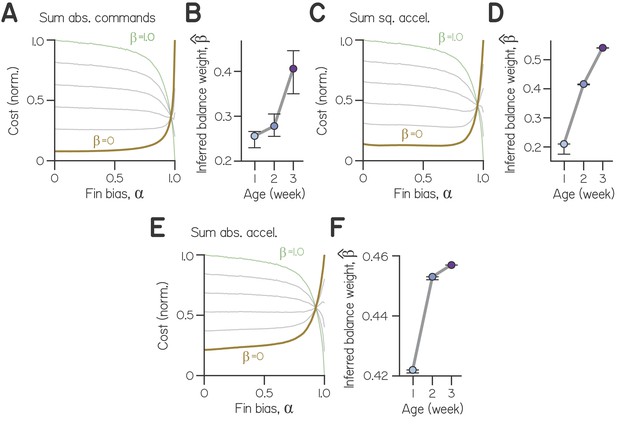
Steering cost functions computed from various formulations of effort.
(A) Cost as a function of fin bias for (balance weights) of 0 (ochre, composed solely of effort), 0.2, 0.4, 0.6, 0.8, and 1 (green), for effort computed as the sum of absolute motor commands. (B) Inferred balance weight as a function of age, with bootstrapped 99% CI, for effort computed as the sum of absolute motor commands. (C) Cost as a function of fin bias for effort computed as the sum of squared accelerations. (D) Inferred balance weight as a function of age, with bootstrapped 99% CI, for effort computed as the sum of squared accelerations. (E) Cost as a function of fin bias for effort computed as the sum of absolute accelerations. (F) Inferred balance weight as a function of age, with bootstrapped 99% CI, for effort computed as the sum of absolute accelerations.
Videos
Video 1
Lateral view of a freely-swimming, two wpf larva producing 4 bouts of upwards motion interleaved by periods of slow sinking.
https://doi.org/10.7554/eLife.45839.006
Video 2
View down the long axis of a freely-swimming, two wpf larva producing 5 bouts of upwards motion with visible pectoral fin abduction.
https://doi.org/10.7554/eLife.45839.007Tables
Table 1
Empirical and simulated swimming properties and morphological measurements as a function of age.
Sigmoid parameters refer to the best-fit logistic function to attack angle vs. body rotation (Equation 1), comprising 4 degrees of freedom. : Spearman’s correlation coefficient.
| Variable | Unit | 4dpf | 1wpf | 2wpf | 3wpf |
|---|---|---|---|---|---|
| Mean attack angle | deg | 0.87 | 1.02 | 4.78 | 8.11 |
| R2 of trajectory and posture | - | 0.86 | 0.91 | 0.78 | 0.66 |
| Deviation from horizontal | deg | 13.91 | 14.08 | 11.91 | 11.30 |
| Swim bout peak speed | mm/s | 11.2 | 13.6 | 13.4 | 14.1 |
| Swim bout duration | s | 0.093 | 0.082 | 0.087 | 0.106 |
| Swim bout displacement | mm | 1.24 | 1.29 | 1.24 | 1.43 |
| Mean bout posture change | deg | 0.10 | −0.23 | 0.24 | 0.21 |
| Standard deviation of bout posture change | deg | 2.21 | 1.84 | 1.84 | 2.10 |
| of attack angle and body rotation | - | 0.305 | 0.269 | 0.379 | 0.368 |
| Proportion of climbs with trajectory > 20° | - | 0.26 | 0.30 | 0.34 | 0.43 |
| Body length | mm | 4.18 | 4.26 | 5.57 | 7.92 |
| Pectoral fin length | mm | 0.41 | 0.42 | 0.61 | 0.90 |
| Fin distance anterior to COM | mm | 0.27 | 0.22 | 0.27 | 0.44 |
| Sigmoid amplitude | deg | 19.28 | 15.71 | 14.30 | 18.79 |
| Sigmoid vertical location, | deg | −3.00 | −1.59 | −3.72 | −3.56 |
| Sigmoid horizontal location, | deg | −0.77 | −0.42 | −1.75 | −1.51 |
| Sigmoid slope, | - | 2.76 | 2.89 | 7.03 | 12.01 |
| Goodness-of-fit (R2) for 4-parameter sigmoid () | - | 0.195 | 0.115 | 0.113 | 0.087 |
| Goodness-of-fit (R2) for 1-parameter sigmoid () | - | 0.193 | 0.109 | 0.092 | 0.086 |
| Empirical fin bias, | - | 0.73 | 0.74 | 0.88 | 0.92 |
| Balance weight in cost function, β | - | 0.12 | 0.12 | 0.18 | 0.32 |
Table 2
Morphology of otog-/- larvae and control siblings (otog+/- and otog+/+ with utricles).
Data listed as mean ± S.D.
| Variable | Unit | Otog-/- | Control |
|---|---|---|---|
| Body length | mm | 4.52 ± 0.32 | 4.53 ± 0.23 |
| Pectoral fin length | mm | 0.43 ± 0.03 | 0.42 ± 0.04 |
| Pectoral fin length | % body length | 9.6 ± 0.6 | 9.3 ± 0.8 |
Table 3
Swim bout properties for otog-/- and Tg(aldoca:GFF);Tg(UAS:KillerRed) larvae.
Data listed as mean ± S.D.
| Variable | Unit | Otog-/-, no utricle | Utricle control | Aldoca::KR lesioned | Aldoca::KR control |
|---|---|---|---|---|---|
| Maximum linear speed | mm·s−1 | 12.4 ± 4.5 | 12.0 ± 4.3 | 10.7 ± 4.3 | 12.7 ± 4.5 |
| Duration | s | 0.084 ± 0.034 | 0.079 ± 0.033 | 0.109 ± 0.070 | 0.120 ± 0.051 |
| Displacement | mm | 1.23 ± 0.61 | 1.13 ± 0.54 | 1.25 ± 0.75 | 1.62 ± 0.71 |
| Maximal pitch-axis angular speed | deg·s−1 | 98.7 ± 73.0 | 90.1 ± 69.0 | 84.4 ± 54.0 | 100.6 ± 61.4 |
| Inter-bout interval | s | 1.22 ± 1.37 | 1.09 ± 1.03 | 2.09 ± 2.30 | 2.12 ± 2.80 |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.45839.016
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
A primal role for the vestibular sense in the development of coordinated locomotion
eLife 8:e45839.
https://doi.org/10.7554/eLife.45839
