The manifold structure of limb coordination in walking Drosophila
- Yale University, United States
Figures
Figure 1 with 2 supplements
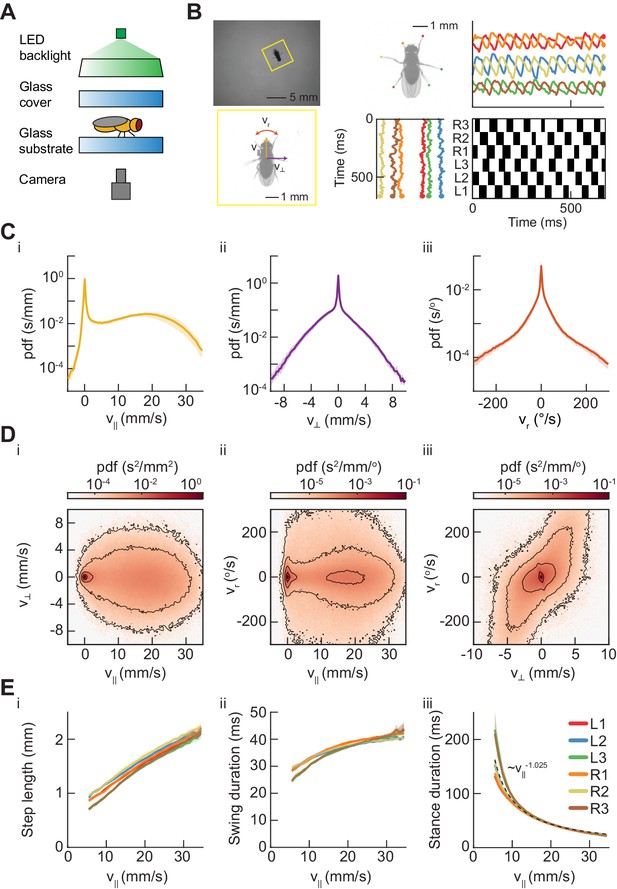
Measurements of body and limb kinematics in freely-walking Drosophila.
(A) Schematic of experimental setup. Fruit flies walk in a circular arena while illuminated from above and tracked from below using a high-speed camera (150 fps). (B) Data transformations from unstructured video to time series variables. Flies are identified in raw camera frames. Individual fly-frames are then grouped and aligned across sequential camera images. Limb positions relative to the fly’s center of mass are converted into time series variables describing limb movements in the egocentric fly frame. The fly’s limbs are binarized into individual periods of swing (black) and stance (white). (C) Probability density functions (PDFs) of three components of body movement: forward walking velocity (), lateral walking velocity (), and rotational velocity (). (D) Joint distributions of body velocity components: forward velocity vs. lateral velocity, forward velocity vs. rotational velocity, and lateral velocity vs. rotational velocity. (E) Mean stepping statistics as a function of forward velocity. Step length in the camera frame increases linearly with forward velocity. Swing duration is roughly constant as forward velocity increases when compared to changes in stance duration. Stance duration decreases inversely with increasing forward velocity. (see Materials and methods). For swing events, n = 58,000 to 59,000 for each limb. For stance events, n = 54,000 to 56,000 for each limb.
Figure 1—figure supplement 1
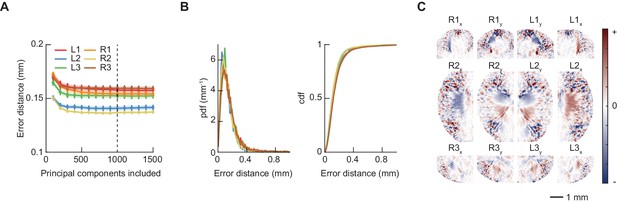
Linear regression accurately identifies footfall positions.
(A) Euclidean error distance (mm) between predicted and actual footfall positions as a function of number of principal components (PCs) included in model, estimated using 10-fold cross-validation. Model used for feature extraction included 1000 PCs. (B) Probability density function (PDF) and cumulative distribution function (CDF) of cross-validated errors (mm) for 1000 PC model used for feature extraction. (C) Learned linear filters that weight oriented fly images (as in Figure 1B) to predict each of the twelve limb positional variables. The spatial extent of each filter is restricted such that correlations between limbs do not bias the resulting predictions (see Materials and methods); this figure shows only the nonzero region of each filter.
Figure 1—figure supplement 2
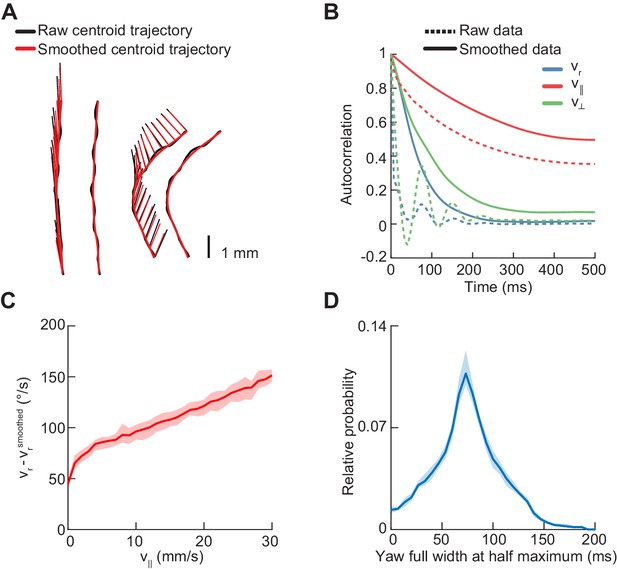
Statistics of centroid kinematic behavior in freely-walking flies.
Error patches show 95% confidence intervals obtained from bootstrap distributions over experiments (N = 8 videos; see Materials and methods). (A) Sample centroid trajectories before and after smoothing. The raw path of the centroid is indicated by a thick black line, and the smoothed path by a thick red line. The heading vector is plotted at 20 ms increments as a thin black line before smoothing, and a thin red line after smoothing. (B) Autocorrelation functions of the yaw velocity (blue), forward velocity (red), and lateral velocity (green) of the fly centroid, before (dashed line) and after (solid line) smoothing with a Gaussian kernel with a standard deviation of 20 ms. (C) Mean absolute deviation of unsmoothed yaw velocity from smoothed yaw velocity as a function of forward velocity. (D) Distribution of full widths at half maxima of yaw rate segments centered around extrema.
Figure 2 with 2 supplements
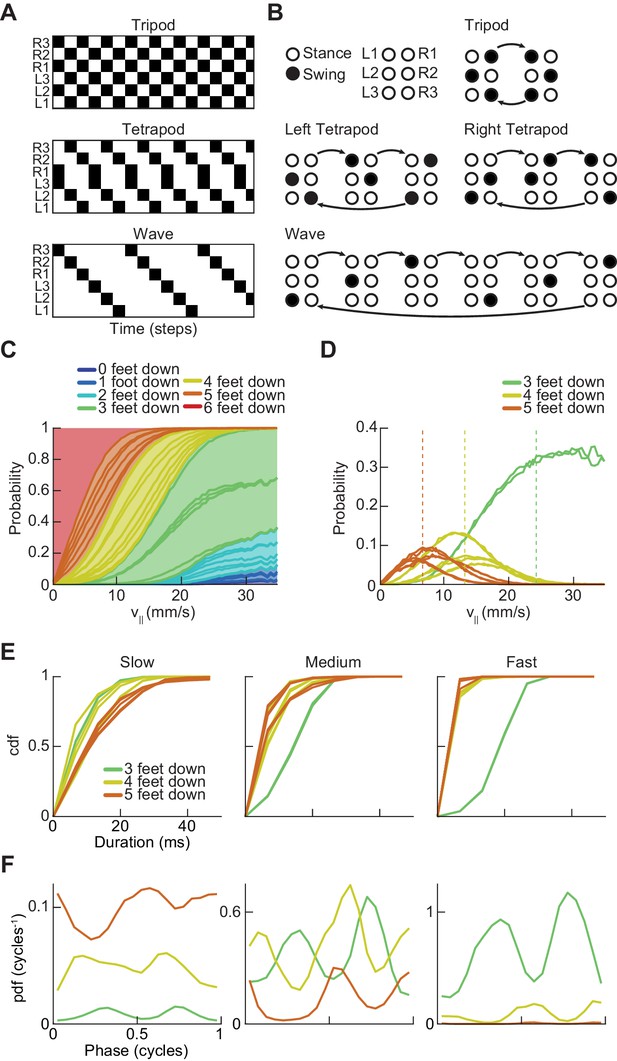
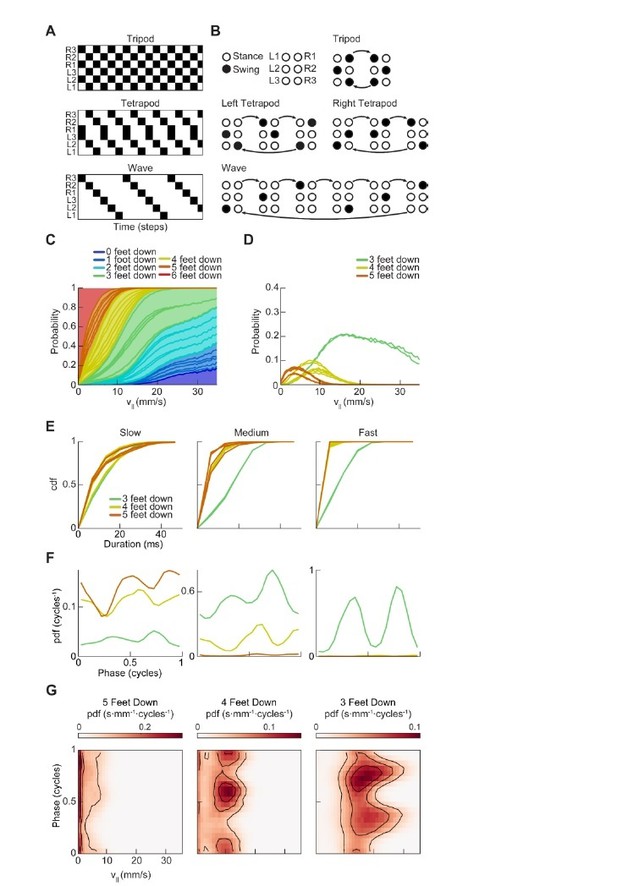
Drosophila use a two-cycle limb coordination pattern across all walking speeds.
(A) Canonical hexapod gaits. In all gaits, limb swings (black) propagate ipsilaterally posterior to anterior on each side of the fly. Tripod gait is defined by three limbs simultaneously swinging at each point in time. Tetrapod gait is defined by two limbs simultaneously swinging at each point in time. Wave gait is defined by each limb swinging individually. (B) Each canonical gait contains a different number of distinct stance configurations, and correspondingly a different number of transitions between these configurations. Tripod gait contains two distinct configurations, tetrapod gait contains three distinct configurations, and wave gait contains six distinct configurations. The ordering of configurations within a cycle is defined by the posterior-to-anterior propagation of ipsilateral swing events (black). (C) Probability of number of feet in stance at each forward walking velocity. Segments within each color represent different configurations within each category. Number of feet in stance decreases as forward walking velocity increases. (D) Probability of canonical stance configurations (from (B)) as a function of forward velocity: tripod (green), tetrapod (yellow), wave gait (orange). Dashed lines indicate the forward speed with maximum probability of each stance category: 24 mm/s, 13 mm/s, and 7 mm/s 3-foot-down, 4-foot-down, and 5-foot-down categories, respectively. (E) Cumulative distribution function (CDF) of stance durations for all canonical gait configurations: tripod (green), tetrapod (yellow), and wave gait (orange). Configuration durations are visualized for bottom, middle, and top thirds of forward velocity distribution: slow walking (0–10.2 mm/s), medium walking (10.2–19 mm/s), and fast walking (>19 mm/s). Tetrapod and wave gait configurations are predominantly transient in all but the slowest walking condition. (F) Relative probability of number of feet in stance as a function of midlimb phase grouped by walking velocity: slow (0–10.2 mm/s), medium (10.2–19 mm/s) and fast walking (>19 mm/s). These probability density functions are normalized such that the integral over phase of the sum of the distributions conditioned on the number of feet down is equal to unity. The number of feet in stance varies as a function of limb phase with a periodicity of two per limb cycle.
Figure 2—figure supplement 1
Estimating limb phases.
Analytic signal decomposition of an example limb position time series. Limb movements in the direction parallel to the fly’s body axis were decomposed into instantaneous measures of phase and amplitude using the discrete-time analytic signal method (see Materials and methods). Phase zero is defined as the maximally posterior point in the limb’s cycle. Phase measurements used throughout the paper were computed in this manner.
Figure 2—figure supplement 2
A two-cycle coordination pattern is used across all walking speeds.
(A) Joint distribution of midlimb phase and forward walking speed conditioned on the number of feet in stance phase reveals two peaks per limb cycle for 5, 4, and 3-foot down conditions across all walking speeds. (B) Relative probability of number of feet in stance as a function of forelimb phase grouped by walking velocity: slow (0–10.2 mm/s), medium (10.2–19 mm/s) and fast walking (>19 mm/s). The number of feet in stance varies as a function of limb phase with a periodicity of two per limb cycle. (C) Relative probability of number of feet in stance as a function of hindlimb phase grouped by walking velocity: slow (0–10.2 mm/s), medium (10.2–19 mm/s) and fast walking (>19 mm/s). The number of feet in stance varies as a function of limb phase with a periodicity of two per limb cycle.
Figure 3 with 3 supplements
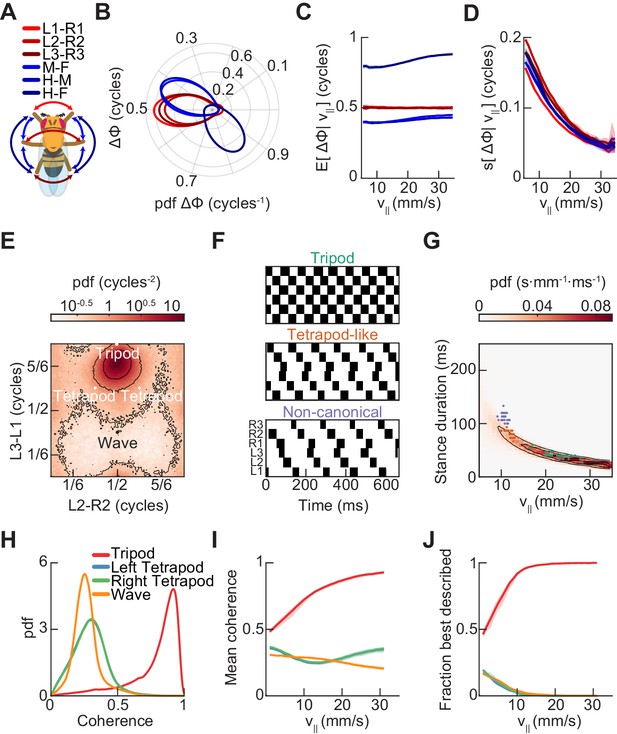
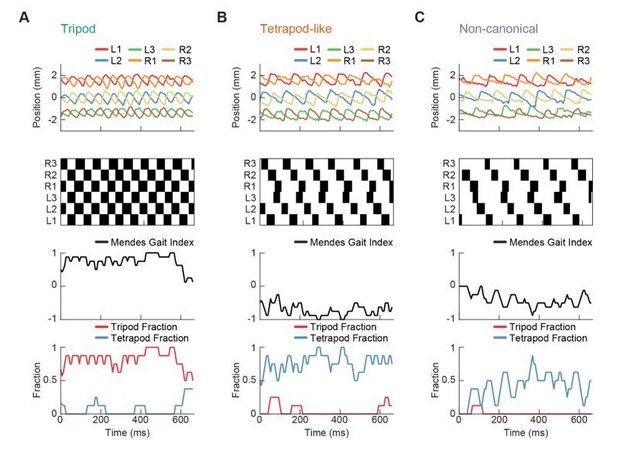
Relative phase measurements reveal a continuum of coordination patterns across all walking speeds with contralateral limbs in antiphase.
(A) Diagram of pairwise limb relative phases, with ipsilateral pairs in blue and contralateral pairs in red. (L1-R1 = Left forelimb – Right forelimb, L2-R2 = Left midlimb – Right midlimb, L3-R3 = Left hindlimb – Right hindlimb, M-F = Midlimbs – Forelimbs, H-M = Hindlimbs – Midlimbs, H-F = Hindlimbs – Forelimbs). (B) Distributions of limb relative phases () for ipsilateral and contralateral pairs across all velocities. (C) Circular means of relative phases as a function of forward velocity. Contralateral relative phases are constant at 0.5 cycles across all walking speeds. Adjacent ipsilateral pairings (mid-fore and hind-mid) approach 0.5 cycles out of phase as forward velocity increases. Hind-fore ipsilateral limb pairings approach being in-phase as forward velocity increases. (D) Angular deviation of pairwise relative limb phases. Variance monotonically decreases in all limb pairings as forward velocity increases. (E) Joint probability distribution of L2-R2 and L3-L1 relative phases reveals a single peak in the distribution. (F) Example trajectories from freely walking fruit flies showing limb coordination patterns similar to canonical tripod (green) and tetrapod (orange), and to a non-canonical gait (purple) in which hind-fore limbs swing together while midlimbs swing individually. (G) Stance duration probability conditioned on forward velocity. All stances from example trajectories overlaid: tripod (green), tetrapod (orange), and non-canonical (purple). (H) Coherence distributions (see Materials and methods) for canonical tripod (red), left tetrapod (blue), right tetrapod (green), and wave gaits (orange). (I) Mean coherence at each forward walking speed for canonical tripod (red), left tetrapod (blue), right tetrapod (green) and wave gaits (orange). (J) Fraction of data best described by each canonical gait as a function of forward walking speed.
Figure 3—figure supplement 1
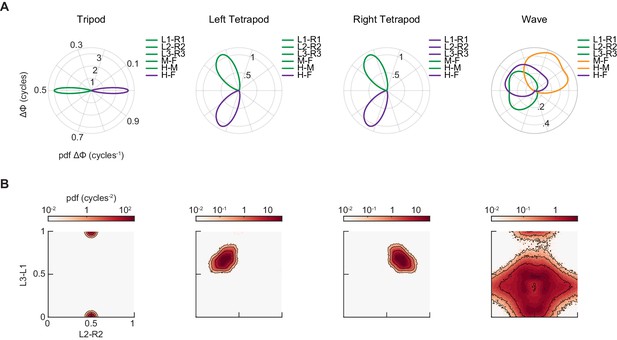
Synthetic canonical gaits differ in relative phasing from the coordination patterns used by free-walking Drosophila.
(A) Distributions of limb relative phases for synthetic tripod, left tetrapod, right tetrapod, and wave gaits. (B) Joint probability distribution of L2-R2 and L3-L1 relative phases for synthetic tripod, left tetrapod, right tetrapod, and wave gaits.
Figure 3—figure supplement 2
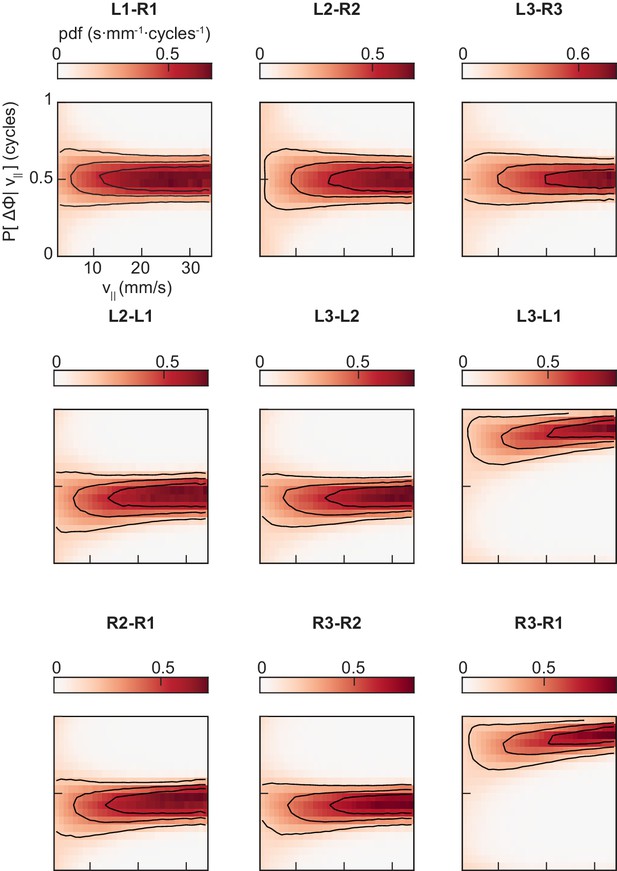
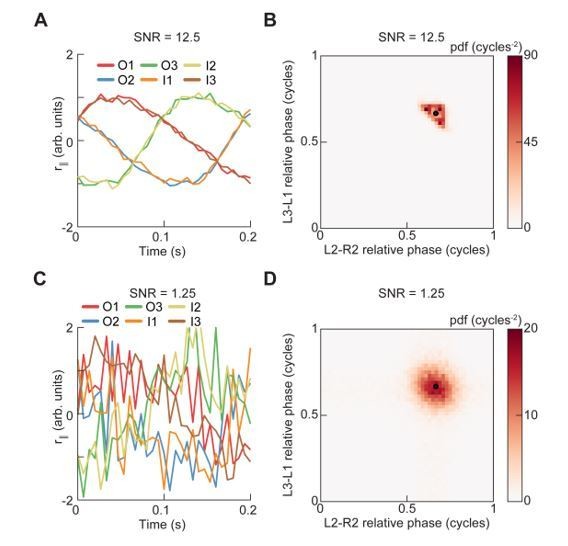
The conditional distributions of pairwise limb relative phases are unimodal at all forward walking speeds.
Probability density functions of each of the nine pairings of limb relative phase shown in Figure 3A–D, conditioned on forward walking speed.
Figure 3—figure supplement 3
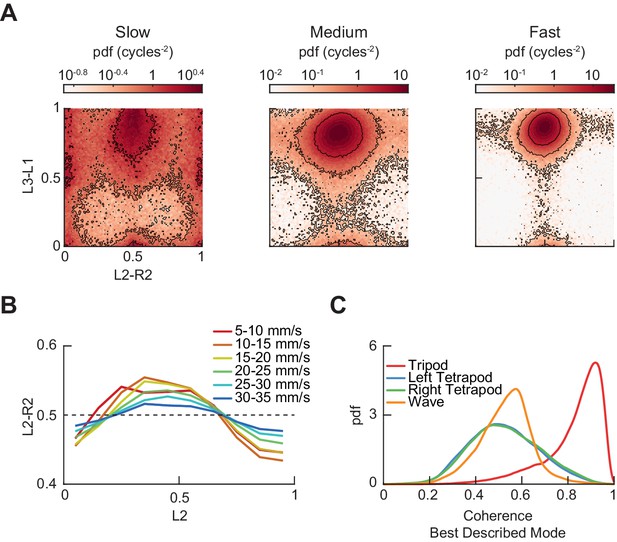
Additional measurements of limb phases.
(A) Joint probability distribution of L2-R2 and L3-L1 relative phases for bottom, middle, and top thirds of forward velocity distribution: slow walking (0–10.2 mm/s), medium walking (10.2–19 mm/s), and fast walking (>19 mm/s). (B) L2-R2 relative phase as a function of L2 limb phase for free-walking wild type flies partitioned by forward walking velocity. Greater range in relative phases occurs at slower forward walking velocities. Error bars are standard error of the mean (SEM). (C) Coherence distributions for timepoints best described by canonical tripod (red), left tetrapod (blue), right tetrapod (green), and wave gaits (orange).
Figure 4 with 5 supplements
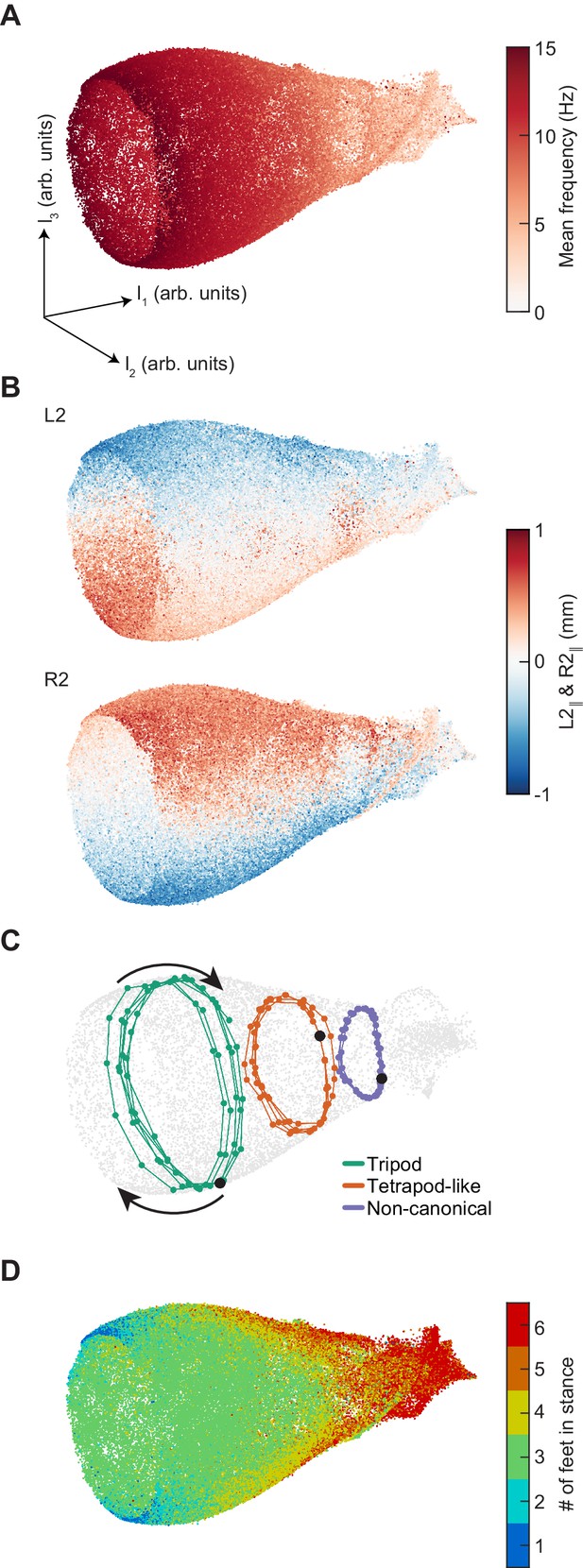
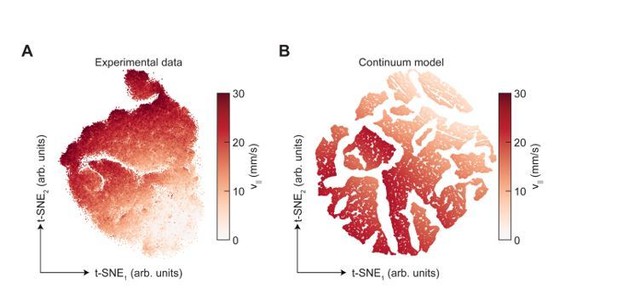
Dimensionality reduction reveals the manifold structure of limb coordination patterns.
(A) UMAP embedding of limb coordinate time series colored by the mean frequency of forward walking. Frequency (correlated with forward walking velocity) maps to the height along the vase-shaped manifold. (B) Embedding colored by the mean-subtracted positions of the left and right midlimbs. The global phase of the walking behavior defines the location along a cross-section of the manifold. (C) Tripod (green), tetrapod-like (orange), and non-canonical (purple) trajectories from Figure 3F–G embedded in the UMAP space. Start of each trajectory is indicated by a black circle. Arrows indicate the trajectory direction. (D) Embedding colored by number of feet in stance. The number of feet in stance changes with a periodicity of two per cycle at all forward walking speeds.
Figure 4—figure supplement 1
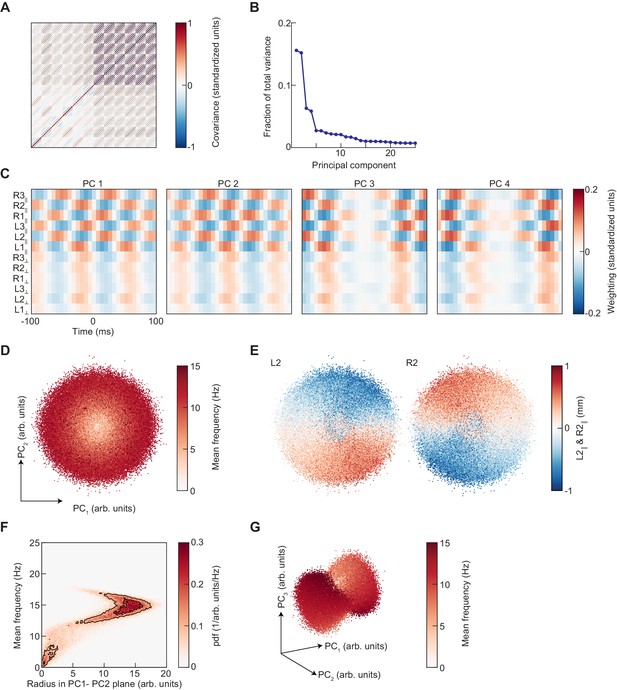
Principal component analysis of limb kinematic data.
(A) The covariance matrix of the segments of standardized limb kinematic data used to generate the UMAP embedding in Figure 4. This matrix is approximately a block-symmetric-Toeplitz matrix. (B) The principal component spectrum of these data is composed of degenerate pairs. (C) The first four principal components of the limb kinematic data used to generate the PCA embedding. PC1 and 2 have approximately equal eigenvalues and are approximately phase-shifted versions of one another. PC3 and 4 are also degenerate and approximately phase-shifted. (D) Scatter plot of the projections of limb kinematic data into the first two principal components, colored by the mean frequency of stepping. (E) As in (D), but colored by the mean-subtracted positions of the left and right midlimbs. (F) Joint distribution of radius in the PC1-PC2 plane as shown in (D) and the mean frequency of stepping. The relationship between frequency and radius is multivalued. (G) As in (D), but for the projection into the first three principal components.
Figure 4—figure supplement 2
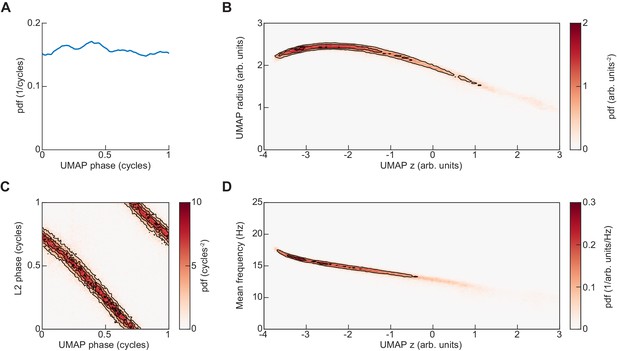
Representation of UMAP embedding in cylindrical coordinates.
(A) The UMAP embedding of limb kinematic data shown in Figure 4 was converted into cylindrical coordinates as , , . Here, the distribution of the resulting UMAP phase angle is shown. (B) Joint distribution of axial and radial coordinates of UMAP embedding. (C) Joint distribution of UMAP phase and L2 instantaneous phase at the central timepoint of the embedded segment. (D) Joint distribution of mean instantaneous frequency and UMAP axial dimension.
Figure 4—figure supplement 3
Contralateral antiphase is preserved at all phases of the global oscillator.
The UMAP embedding of limb kinematic data shown in Figure 4, colored by the instantaneous phases of the left and right midlimbs at the center point of each segment.
Figure 4—figure supplement 4
Changing the segment duration dilates the axial extent of the UMAP manifold while maintaining the same structure.
(A) UMAP embedding of 100 ms segments of limb positional data, colored by mean stepping frequency (see Figure 4A). (B) As in (A), but for 400 ms segments. (C) As in (A), but colored by the position of the right midlimb in the direction parallel to the body axis (see Figure 4B). (D) As in (C), but for 400 ms segments.
Figure 4—figure supplement 5
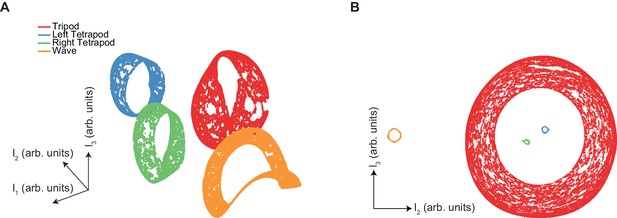
The manifold structure of synthetic canonical gaits differs qualitatively from that of free-walking Drosophila.
(A) UMAP embedding (see Materials and methods) of synthetic tripod (red), left tetrapod (blue), right tetrapod (green), and wave gaits (orange) reveals separate manifolds for each canonical gait type. Tripod, tetrapod, and wave gaits occur with equal abundance in this embedding. (B) Separation of UMAP manifolds remains even with low abundance of non-tripod gaits. Gaits represented different fractions of the input data: tripod (red) 98%, left tetrapod (blue) 0.5%, right tetrapod (green) 0.5%, wave gait (orange) 1%.
Figure 5 with 1 supplement
A single-parameter model with speed-independent coupling predicts a continuum of inter-limb coordination patterns.
(A) A single-parameter phase oscillator model to generate metachronal waves (see Materials and methods). The frequency of metachronal waves is determined by a single parameter, stance. Limb oscillators are coupled by constant unidirectional inhibition from posterior limbs to anterior limbs. (B) A minimal model of spontaneous walking in the fruit fly may be obtained by linking two of the units diagrammed in (A) with bidirectional contralateral coupling. Forward walking speed is determined solely by stance duration. Example swing-stance plots illustrate the ability to generate walking patterns similar to canonical tripod (v||=25 mm/s) and tetrapod-like gaits (v||=15 mm/s). Additionally, this model generates the non-canonical limb coordination pattern identified in our data (v||=10 mm/s), in which midlimbs swing independently while contralateral fore and hind limbs swing together. As observed in our experimental data, the tetrapod-like pattern generated by this model deviates from canonical tetrapod as relative phases between contralateral limbs are antiphase. Example trajectories from Figure 3F are presented for comparison to model trajectories. This model was used to generate the data analyzed in panels (C–G). (C) Relative probability of the number of feet in stance as a function of forward walking speed. As walking speed increases, the number of feet in stance decreases. (D) Relative probability of number of feet in stance as a function of midlimb phase for bottom, middle, and top thirds of forward velocity distribution. The number of feet down oscillates with a frequency of two per single-limb-stride. (E) Circular means of limb relative phases for each pairwise relationship as a function of forward velocity. Consistent with experimental data, contralateral relative phases are constant at ½ cycles across all walking speeds. Adjacent ipsilateral pairings (mid-fore and hind-mid) approach antiphase as walking frequency (forward velocity) increases. Hind-fore ipsilateral limb pairings approach being in-phase as forward velocity increases. (F) Angular deviation of pairwise relative limb phases. Variance of relative phases decreases in all limb pairings as forward velocity increases. (G) UMAP embedding of model-generated trajectories. All trajectories lie on a single manifold.
Figure 5—figure supplement 1
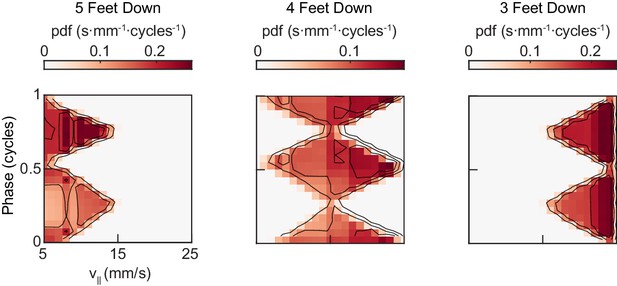
A single-parameter model generates a two-cycle coordination pattern across all walking speeds.
Model-generated joint distribution of midlimb phase and forward walking speed shows two peaks per limb cycle for 5, 4, and 3-foot down conditions.
Figure 6 with 1 supplement
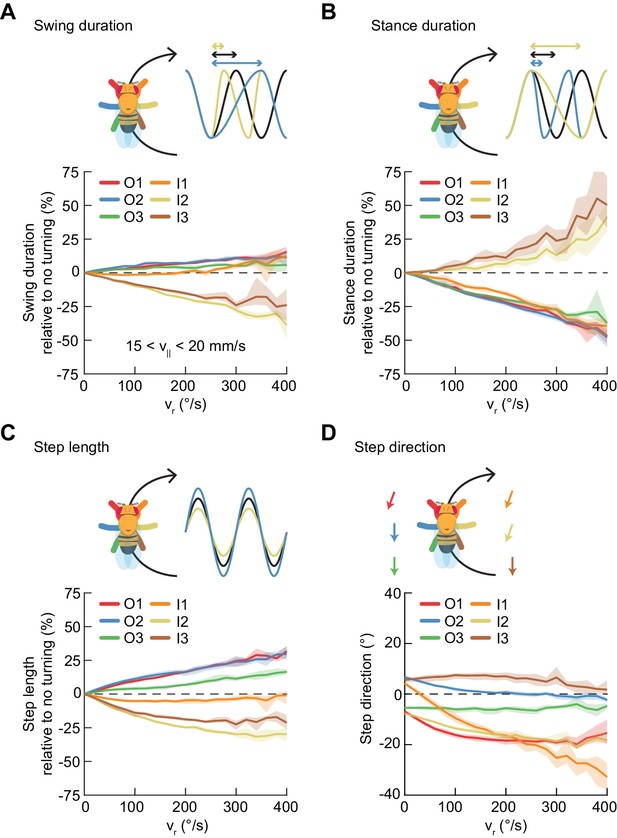
Asymmetric, segment-specific modulations of limb movement underlie turning.
Error patches show 95% confidence intervals of the mean obtained from bootstrap distributions over experiments (N = 8 videos; see Materials and methods). (A) Modulation of swing duration in individual limbs relative to straight walking as a function of symmetrized yaw velocity. Red, blue and green indicate the outside fore-, mid-, and hindlimbs respectively. Orange, yellow and brown indicate the inside fore-, mid-, and hindlimbs respectively. To exclude the effect of forward speed modulation on limb movement parameters, the analysis is restricted to forward velocities between 15 and 20 mm/s. The swing durations of the inside mid- and hindlimbs decrease with increasing yaw rate while those of the remaining limbs increase slightly with yaw rate. (B) As in (A), but for stance duration. The stance durations of the inside mid- and hindlimbs increase with increasing yaw rate while those of the remaining limbs decrease with yaw rate. (C) As in (A), but for step length. The step lengths of the outside limbs increase with yaw rate, while those of the inside mid- and hindlimbs decrease with yaw rate and that of the inside forelimb is barely modulated. (D) As in (A), but for step direction. The direction of steps in the inside and outside forelimbs is shifted such that their movements are directed outwards relative to the curvature of its path.
Figure 6—figure supplement 1
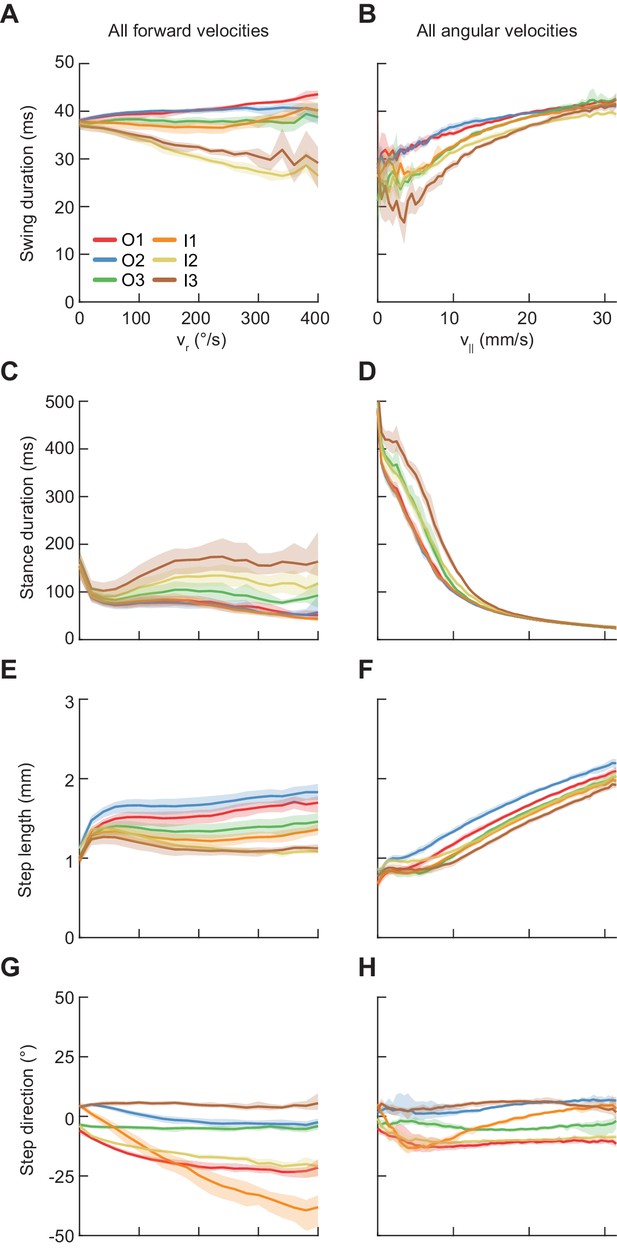
Average modulations of limb movement parameters.
Error patches show 95% confidence intervals of the mean obtained from bootstrap distributions over experiments (N = 8 videos; see Materials and methods). (A) Average swing duration in individual limbs conditioned on symmetrized yaw velocity. Red, blue and green indicate the outside fore-, mid-, and hindlimbs respectively. Orange, yellow and brown indicate the inside fore-, mid-, and hindlimbs respectively. (B) As in (A), but conditioned on forward velocity. (C) As in (A), but for stance duration. (D) As in (C), but conditioned on forward velocity. (E) As in (A), but for step length. (F) As in (E), but conditioned on forward velocity. (G) As in (A), but for step direction. (H) As in (G), but conditioned on forward velocity.
Figure 7
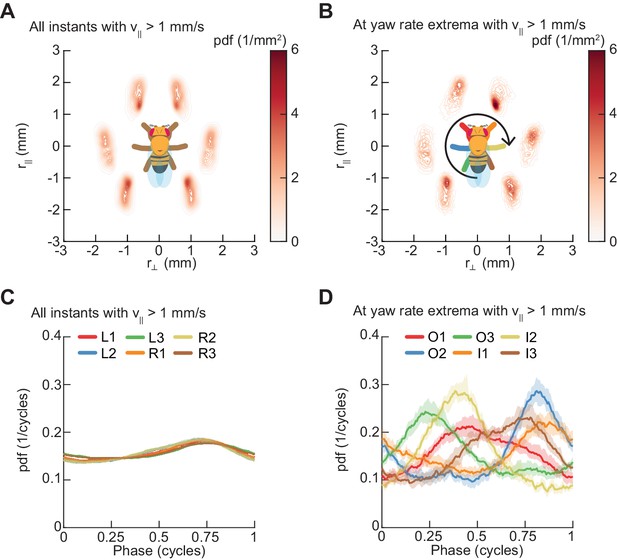
Spontaneous turns are aligned to preferred phases of the limb oscillator.
Error patches show 95% confidence intervals obtained from bootstrap distributions over experiments (N = 8 videos; see Materials and methods). (A) Probability density function of limb positions in the egocentric frame of the fly over all walking behaviors. (B) As in (A), but at yaw rate extrema. The tripod containing the inside forelimb is in nearly its most posterior position, while the tripod containing the outside forelimb is in nearly its most anterior position. (C) Circular probability density functions of the instantaneous phases of each limb over all walking behaviors. Phases between ½ and 1, corresponding to stance phase, are more probable than phases between 0 and ½, corresponding to swing phase, due to the fact that the duration of stance phase is on average greater than that during swing phase. (D) As in (C), but at yaw rate extrema. There exists a preferred phase of each limb at which yaw rate extrema occur, which differs significantly from the corresponding time-invariant distribution (see Materials and methods).
Figure 8
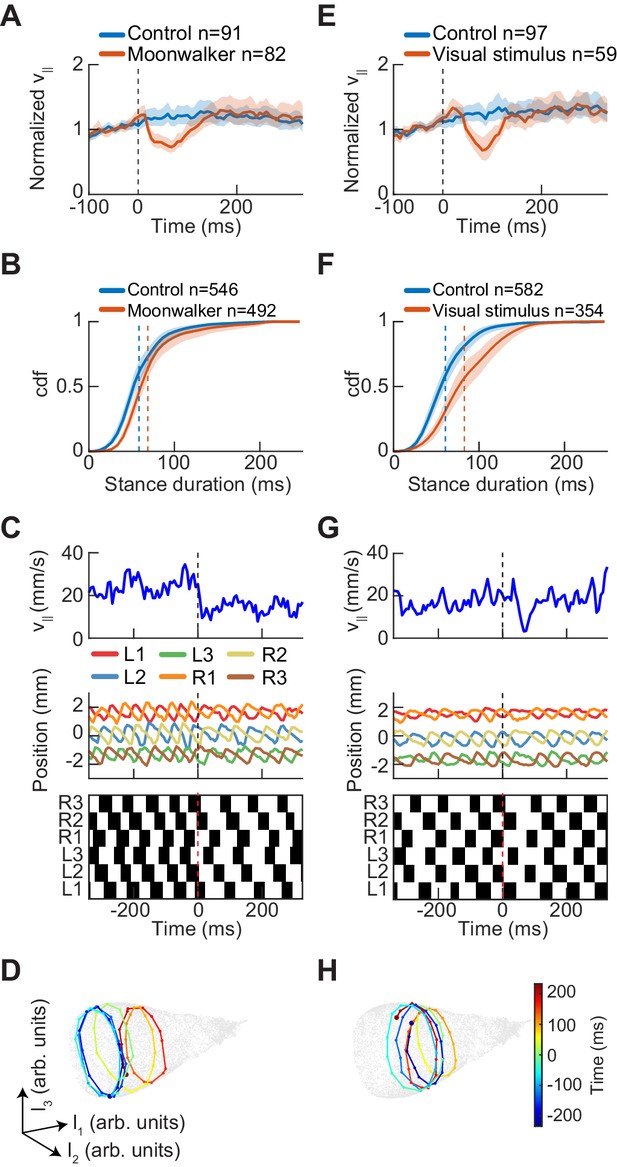
Experimental perturbations of walking speed modulate stance duration.
(A) Drosophila normalized forward speed over time in response to 8 ms optogenetic activation of moonwalker neurons (red, n = 82) versus random trigger control (blue, n = 91). (B) Cumulative distribution function of first stance duration post perturbation for all limbs for moonwalker manipulation (red, n = 492) versus random trigger control (blue, n = 546). Includes stance durations from all six limbs. Distributions are significantly different as measured by a two-sample Kolmogorov-Smirnov test (N = 91, 82; p<0.05; D = 0.1965). (C) Single trial of walking over time in response to moonwalker activation. Forward walking speed (blue) over time. Limb positions in the direction parallel to the fly’s body axis over time. Step plot for the fly over time with swing (black) and stance (white) in each of the limbs. Post manipulation, stance duration increases in all limbs. (D) The trajectory of a single trial in the UMAP embedding space shows that moonwalker activation induces shifts along the length of the manifold. The time relative to activation onset at the center of each embedded trajectory is indicated by color, with dark blue corresponding to times before onset ( ms), green corresponding to the onset of activation ( ms), and dark red corresponding to times after activation ( ms). (E) Drosophila normalized forward speed over time in response to 50 ms translation of random dot stimuli moving at 720, 960, or 1440 o/s (red, n = 59) versus random trigger control (blue, n = 97). (F) Cumulative distribution function of first stance duration post perturbation for all limbs for visual stimulus manipulation (red, n = 354) versus random trigger control (blue, n = 582). Includes stance durations from all six limbs. Distributions are significantly different as measured by a two-sample Kolmogorov-Smirnov test (N = 97, 59; p<0.05; D = 0.2834). (G) As in (C), but for visual stimulation. (H) As in (D), but for visual stimulation.
Author response image 1
Replication of Figure 2 with halved swing/stance separation threshold.
Author response image 2
Analysis of phase extraction with high SNR (A and B) and low SNR (C and D).
Author response image 3
Example trajectories with gait index analysis from Mendes et al., 2013.
Author response image 4
t-SNE embedding of limb position data, colored by forward walking speed.
(A) shows experimental limb positional data, while (B) shows data generated using the continuum model presented in Figure 5 of the manuscript.
Videos
Video 1
This movie shows a fly walking in our arena with annotated body and limb features.
Video shows annotations in both the camera and egocentric frame of the fly. Body orientation is indicated with a yellow triangle. Limb positions are red (L1), blue (L2), green (L3), orange (R1), yellow (R2), and brown (R3).
Video 2
This movie shows a fly in its egocentric frame with annotations for each of the individual limbs.
Limb position variables are shown as time series in the direction parallel and perpendicular to the fly’s major axis. Limb positions are red (L1), blue (L2), green (L3), orange (R1), yellow (R2), and brown (R3). Swing (black) and stance (white) events for each of the limbs are shown as a function of time.
Video 3
This movie shows a grid of 25 fly trajectories seen in the egocentric frame.
Limb positions are annotated with red (L1), blue (L2), green (L3), orange (R1), yellow (R2), and brown (R3).
Tables
Table 1
Fly strains.
https://doi.org/10.7554/eLife.46409.028| Genotype | Source | Experiment | Figure | |
|---|---|---|---|---|
| Wild type | +; +; + | (Gohl et al., 2011) | Free-walking; Visual stimulus induced slowing | 1–8 |
| Moonwalker > Chrimson | +; +; VT-050660-Gal4/UAS-Chrimson | (Bidaye et al., 2014) | Optogenetic induced slowing | 8 |
Table 2
Phase templates for canonical gait coherence analysis (Collins and Stewart, 1993).
Limb ordering is (L1, L2, L3, R1, R2, R3).
| Canonical gait | Phase template (cycles) |
|---|---|
| Tripod | [0, 1/2, 0, 1/2, 0, 1/2] |
| Left tetrapod | [1/3, 2/3, 0, 0, 1/3, 2/3] |
| Right tetrapod | [2/3, 0, 1/3, 0, 1/3, 2/3] |
| Wave | [1/6, 1/3, 1/2, 2/3, 5/6, 0] |
Table 3
Parameters used for model in Figure 5.
https://doi.org/10.7554/eLife.46409.031| Parameter | Value |
|---|---|
| 1/8 | |
| 40 ms | |
| 40–210 ms |
Table 4
Two-sample Monte Carlo resampling tests using the Kuiper V-statistic against the null hypothesis that the distribution of phases at yaw extrema is indistinguishable from that over all instants (105 permutations, N = 8 videos).
https://doi.org/10.7554/eLife.46409.026| Limb | V-statistic | p-Value | 95% CI for p-value |
|---|---|---|---|
| O1 | 1.08 × 10−1 | <10−5 | [0, 3.68 × 10−5] |
| O2 | 1.67 × 10−1 | <10−5 | [0, 3.68 × 10−5] |
| O3 | 1.77 × 10−1 | <10−5 | [0, 3.68 × 10−5] |
| I1 | 1.07 × 10−1 | <10−5 | [0, 3.68 × 10−5] |
| I2 | 2.33 × 10−1 | <10−5 | [0, 3.68 × 10−5] |
| I3 | 1.16 × 10−1 | <10−5 | [0, 3.68 × 10−5] |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.46409.032
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The manifold structure of limb coordination in walking Drosophila
eLife 8:e46409.
https://doi.org/10.7554/eLife.46409
