An image-computable model for the stimulus selectivity of gamma oscillations
Figures
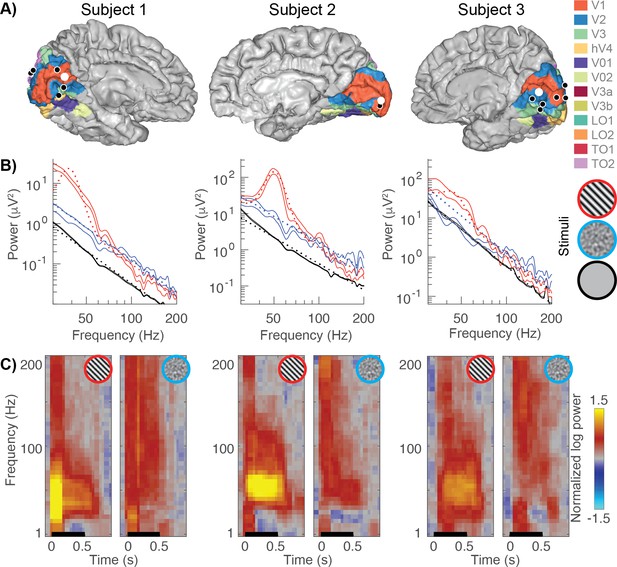
Example broadband and gamma responses to grating and noise stimuli.
(A) Location of the electrodes implanted in each subject (black and white dots) rendered on estimates of early visual areas (Benson and Winawer, 2018; Benson et al., 2012). (B) The power spectra for example electrodes (white dots from panel A). Power spectra are shown on a double logarithmic plot for a grating stimulus (red, stimulus number 45), a noise pattern (blue, stimulus number 83) and the baseline condition (black). The solid lines indicate the data (68% confidence interval from bootstrapping). The dotted lines indicate the fits to the data: stimulus-induced responses are modeled as a baseline linear fit (black) plus a constant and Gaussian to capture broadband and narrowband stimulus-specific responses, respectively. (C) Time-frequency plots (spectrograms) for the same electrodes. The black line indicates stimulus timing (500 ms). All spectrograms are normalized with respect to the same baseline: the inter-stimulus interval between all trials (from 250 to 500 ms after stimulus offset). Spectrograms are cut off at a maximum power of ±1.5 log10 units. The multitaper approach results in a temporal smoothing of 200 ms and a frequency smoothing of ±15 Hz. Spectrograms represent averages across all trials of a given stimulus type. Code to reproduce this figure can be found on GitHub (Hermes, 2019).
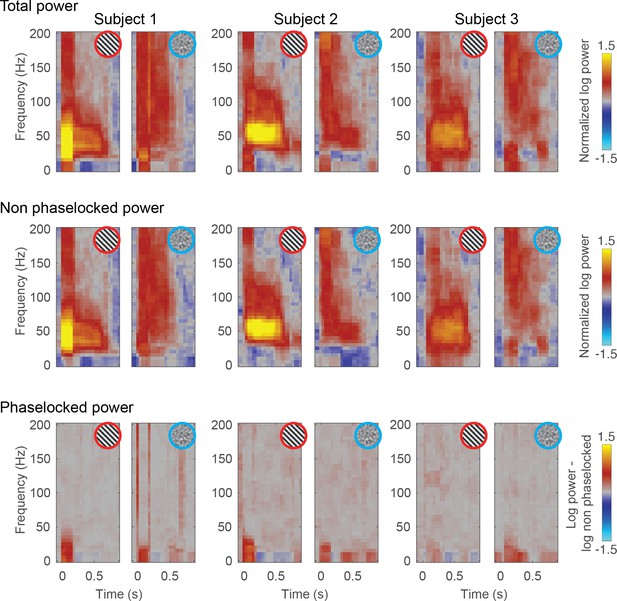
Phase locking plots.
In order to calculate the phase-locked power, we used methods described by Mike X Cohen (Cohen, 2014). We first calculated the total power as we did in the manuscript, and is shown in the top row of the plot and in manuscript Figure 1C (performing the time-frequency decomposition using a multitaper approach [Percival and Walden, 1993] using chronux (http://www.chronux.org/ [Mitra and Bokil, 2008]). We used a moving window of 200 ms with 50 ms overlap and five tapers, resulting in a frequency resolution of 5 Hz and a spectral smoothing of ±15 Hz). We then computed the ERP and subtracted it from each trial via regression. We assume that the ERP is the phase locked signal and regressing it from each trial gives the non-phase-locked signal. We then calculated the time-frequency representation of this non-phase-locked signal (middle row). Finally, the non-phase-locked power was subtracted from the total power, producing the phase-locked power (bottom row). The phase locked responses contained most power in the lower frequencies rather than affecting the gamma and broadband responses of interest.
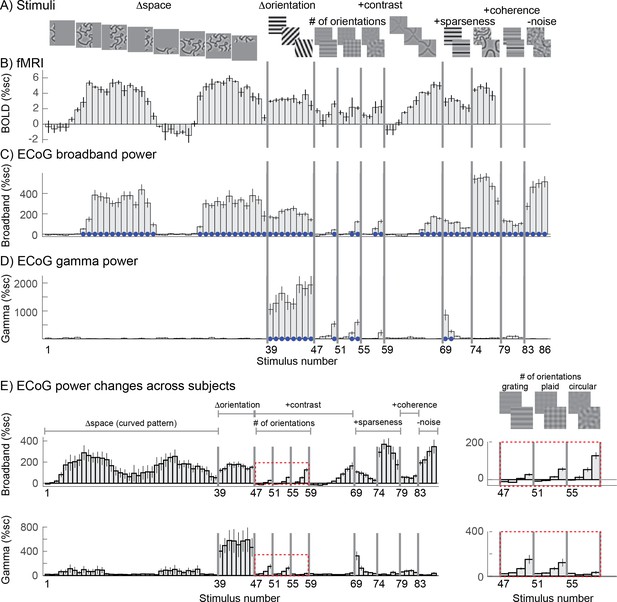
Stimulus selectivity for BOLD, broadband, and gamma.
Responses in human V1 to different images expressed as percent signal change above baseline. (A) The images were identical to those used in a prior fMRI study, with a few additions, and are grouped into several stimulus categories: SPACE (1 to 38), ORIENTATION (39 to 46), CONTRAST (47 to 68), SPARSITY (69 to 78), COHERENCE (79 to 86). Larger versions of the stimuli are shown in Figure 2—figure supplement 1–5. (B) The fMRI BOLD response in one V1 voxel whose pRF location is matched to the electrode shown in C and D (replotted from Kay et al., 2013b). (C) The ECoG broadband response for all 86 images from a single electrode (Figure 1A, left). (D) The ECoG narrowband gamma response for all 86 images, recorded in the same electrode. (E) Broadband (top) and narrowband (bottom) gamma responses to 86 stimuli averaged across the 15 electrodes in V1-V3. Insets (right) show a zoomed-in view of how the responses vary with four contrast levels and different numbers of component gratings: 1, ‘grating’, 2 ‘plaid’, or 16 ‘circular’. Within each type of pattern, the four bars are responses to stimuli with increasing stimulus contrast. In panels C-D, blue dots indicate significant responses (p<0.05 by bootstrap). In panels B-D, error bars represent the 68% range by bootstrapping across trials. In panel E, error bars represent the 68% range by bootstrapping across electrodes. Code to reproduce this figure can be found on GitHub (Hermes, 2019).

Stimuli 1-20.
These 86 stimuli were shown in random order for 500 ms to the subjects. The top stimulus shows how a fixation dot was presented in the center, and the subjects had to indicate when it changed color. Stimulus 1–38 different in the space that was covered by the contrast pattern. Stimulus 39–46 contained gratings of varying orientation. Stimulus 47–50 contained gratings (one orientation) of increasing contrast. Stimulus 51–54 contained plaids (two orientations) of increasing contrast. Stimulus 55–58 contained curved patterns (multiple orientations) of increasing contrast. Stimulus 59–68 contained curved patterns of increasing contrast. Stimulus 69–73 contained gratings of increasing sparseness and stimulus 74–78 contained curved patterns of increasing sparseness. Stimulus 79–82 was a grating increasing in coherence. Stimulus 83–86 contained a curved pattern decreasing in the amount of noise.

Stimuli 21-40.
https://doi.org/10.7554/eLife.47035.006
Stimuli 41-60.
https://doi.org/10.7554/eLife.47035.007
Stimuli 61-80.
https://doi.org/10.7554/eLife.47035.008
Stimuli 81-86.
https://doi.org/10.7554/eLife.47035.009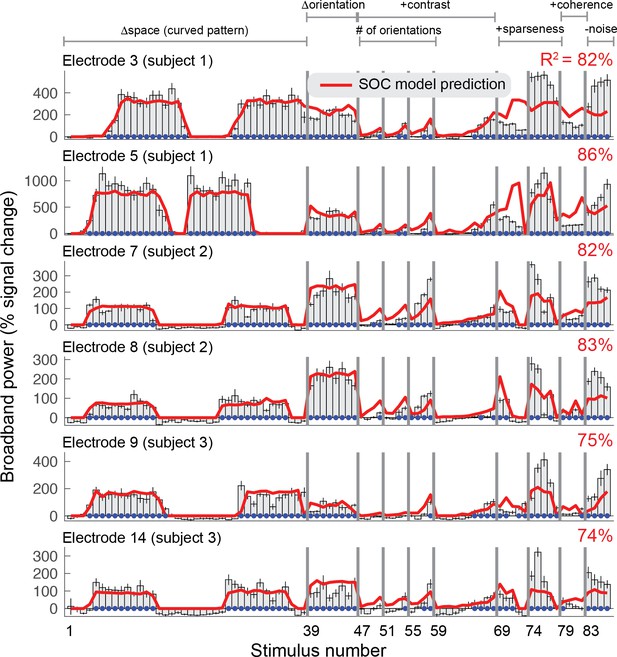
Second-order contrast (SOC) model accounts for ECoG broadband responses.
Each row shows the percent signal change in ECoG broadband power for all 86 stimuli for six of the 15 electrodes on V1, V2 or V3. Error bars display the 68% range for bootstrapped responses (bootstrapped across repeated presentations of the same stimuli). The SOC model was fit to these data using leave-one-stimulus-out cross-validation. The cross-validated predictions and amount of variance explained are shown in red. The blue dots indicate that the stimulus response was significantly greater than baseline (p<0.05, bootstrap test). Code to reproduce this figure can be found on GitHub (Hermes, 2019).
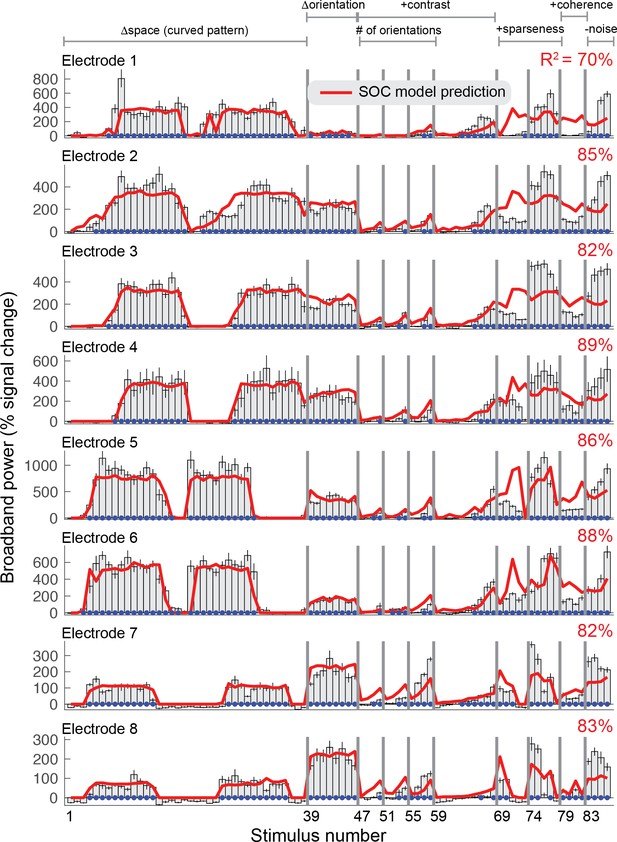
Second-order contrast (SOC) model accounts for ECoG broadband responses for electrode 1–8.
Each row shows the percent signal change in ECoG broadband power for all 86 stimuli for electrodes 1–8 on V1, V2 or V3. Error bars display the 68% range for bootstrapped responses (bootstrapped across repeated presentations of the same stimuli). The SOC model was fit to these data using leave-one-stimulus-out cross-validation. The cross-validated predictions and amount of variance explained are shown in red. The blue dots indicate that the stimulus response differed significantly from baseline (p<0.05 by bootstrap).
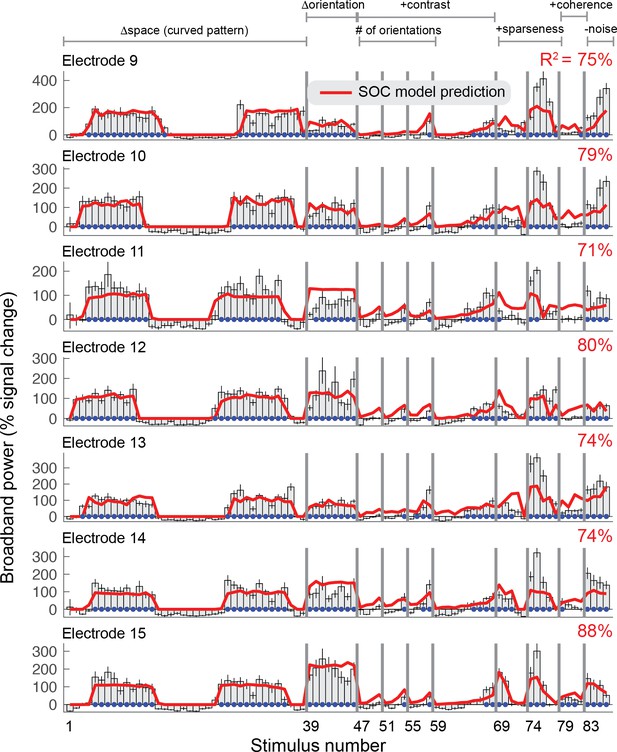
Second-order contrast (SOC) model accounts for ECoG broadband responses for electrodes 9–15.
Each row shows the percent signal change in ECoG broadband power for all 86 stimuli for electrodes 9–15 on V1, V2 or V3. Error bars display the 68% range for bootstrapped responses (bootstrapped across repeated presentations of the same stimuli). The SOC model was fit to these data using leave-one-stimulus-out cross-validation. The cross-validated predictions and amount of variance explained are shown in red. The blue dots indicate that the stimulus response differed significantly from baseline (p<0.05 by bootstrap).

Broadband power changes calculated for a time window after the evoked response.
Broadband responses for the total window from 0 to 500 ms (left – same as Figure 3) and in the window 200–500 ms, which avoids the evoked response (right). Blue dots indicate that responses differed significantly from baseline (p<0.05 by bootstrap).

Orientation Variance (OV) model of gamma responses and the Second Order Contrast (SOC) model of broadband responses.
Top: in the OV model, responses are largely driven by contrast and variance across orientations in the population receptive field. (A) Oriented contrast energy. Images are filtered with quadrature pair Gabor filters occurring at eight orientations. The quadrature pairs are summed across phase, resulting in eight images with contrast energy for each orientation. (B) The contrast energy within each of these eight images is summed within a population receptive field defined by a Gaussian with parameters x, y and σ. This results in eight values, indicating the summed contrast energy within the pRF for each orientation. (C) Variance is calculated across these eight values, followed by a power-law nonlinearity (n) and a gain (g). Intuitively, the model predicts a large response when only one or a few orientations have high contrast energy and a low response when all orientations have similar contrast energy. Bottom: in the SOC model, responses are driven by contrast and variance across space in the population receptive field. (D) Contrast energy. The first step that generates oriented contrast energy images is the same as the OV model (see A). (E) Divisive normalization and summation across orientations. This results in a contrast image where information about variance across orientation is lost. (F) The image is then filtered by the population receptive field defined by a Gaussian with parameters x, y and σ and the variance in contrast compared to the mean contrast is calculated with parameter c indicating the extent to which the output is driven by the mean contrast versus the variance in contrast. (G) A power-law nonlinearity (n) and a gain (g) finally yields the predicted response. Intuitively, the model predicts a large response for increasing contrast and the c parameter determines the extent to which the predicted response is enhanced by variation in contrast across the pRF.
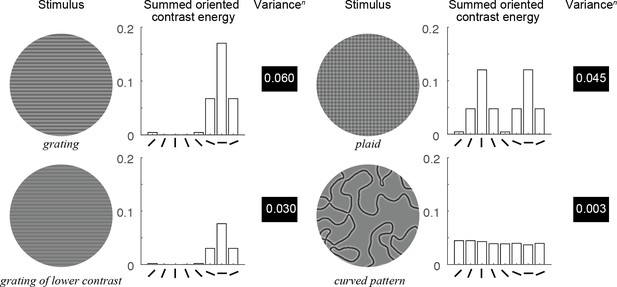
Behavior of the OV model.
For each example stimulus, the contrast energy within each of 8 orientation bands is summed across the image (bar plots), which simulates the response for a large receptive field spanning the whole image. The variancen (with n = 0.5) across these eight values, monotonically related to the output of the model, is displayed next to the bar plots. This value increases with stimulus contrast (upper left versus lower left) and increases with sparsity of orientations: the high-contrast grating with few orientations present (upper left) has a higher output than the plaid with several orientations present (upper right), which in turn has a higher output than the curved pattern with many orientations (lower right). Code to reproduce this figure can be found on GitHub (Hermes, 2019).
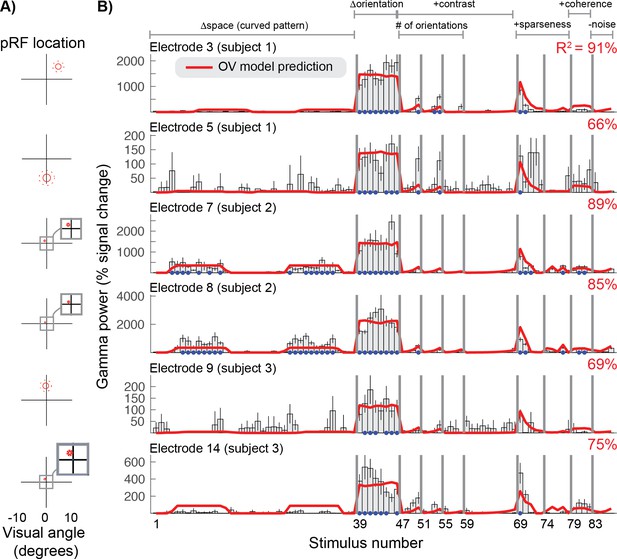
Orientation Variance (OV) model predicts selectivity of gamma responses.
(A) The population receptive field for each electrode was defined by a Gaussian, indicated by the 1- and 2-sd contours (solid and dotted red lines). (B) The gamma power in percent signal change for six of the 15 electrodes (rows) for all 86 stimuli. Error bars display the 68% range for the bootstrapped responses. The cross-validated predictions of the OV model and overall variance explained (R2) are shown in red. The blue dots indicate that the stimulus response was significantly greater than baseline (p<0.05 by bootstrap test). Code to reproduce this figure can be found on GitHub (Hermes, 2019).

Orientation Variance (OV) model predicts selectivity of gamma responses for electrodes 1–8.
(A) The population receptive field for each electrode was defined by a Gaussian, indicated by the 1- and 2-sd contours (solid and dotted red lines). (B) The gamma power in percent signal change was calculated for electrodes 1–8 (rows) for all 86 stimuli. Error bars display the 68% range for the bootstrapped responses. The cross-validated predictions of the OV model and overall variance explained (R2) are shown in red. The blue dots indicate that the stimulus response differed significantly from baseline (p<0.05 by bootstrap).
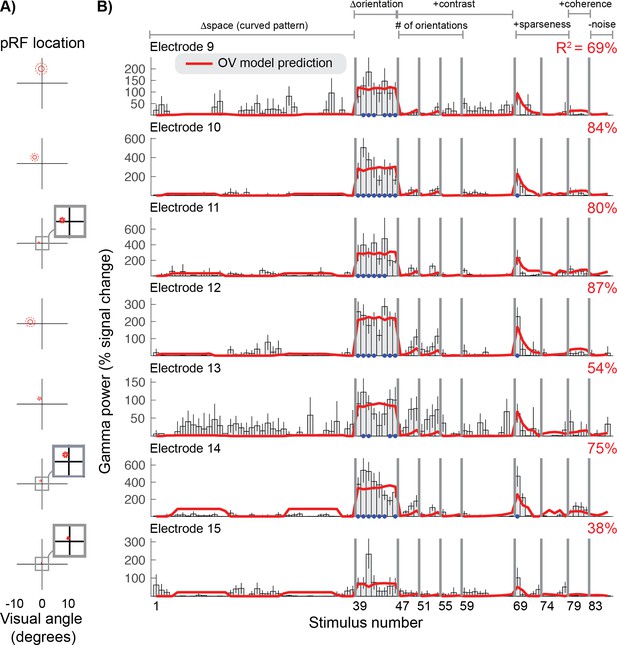
Orientation Variance (OV) model predicts selectivity of gamma responses for electrodes 9–15.
(A) The population receptive field for each electrode was defined by a Gaussian, indicated by the 1- and 2-sd contours (solid and dotted red lines). (B) The gamma power in percent signal change was calculated for electrodes 9–15 (rows) for all 86 stimuli. Error bars display the 68% range for the bootstrapped responses. The cross-validated predictions of the OV model and overall variance explained (R2) are shown in red. The blue dots indicate that the stimulus response differed significantly from baseline (p<0.05 by bootstrap).
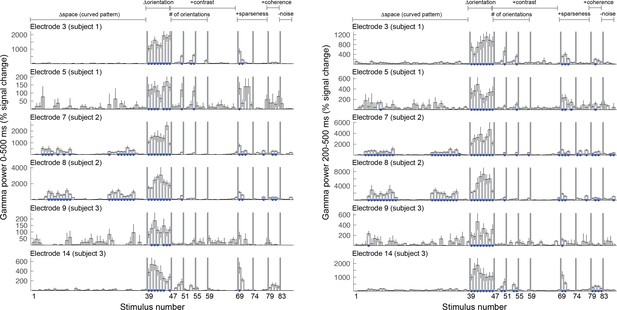
Gamma power changes calculated for a timewindow after the evoked response.
Gamma responses for the total window from 0 to 500 ms window (left – same as Figure 6) and in the window 200–500 ms, which avoids the evoked response (right). Blue dots indicate that responses differed significantly from baseline (p<0.05 by bootstrap).
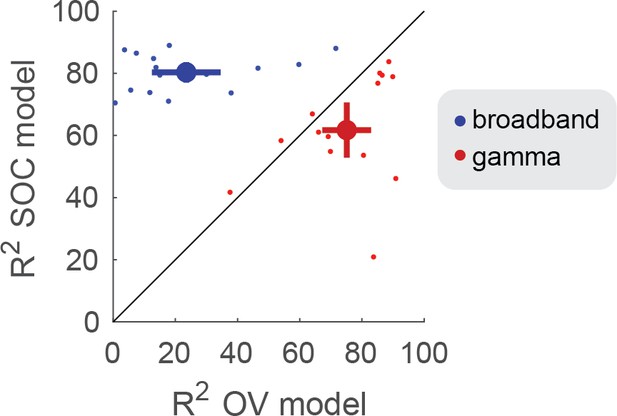
OV and SOC model performance on broadband and gamma power.
The model performance (R2) was quantified using the coefficient of determination. The x-axis shows the model performance of the OV model fit to the narrowband gamma power (red) and broadband power (blue). The y-axis shows the model performance of the SOC model fit to the gamma power (red) and broadband power (blue). The small dots show the performance for individual electrodes and the large dot indicates the mean + /- two standard errors. Code to reproduce this figure can be found on GitHub (Hermes, 2019).
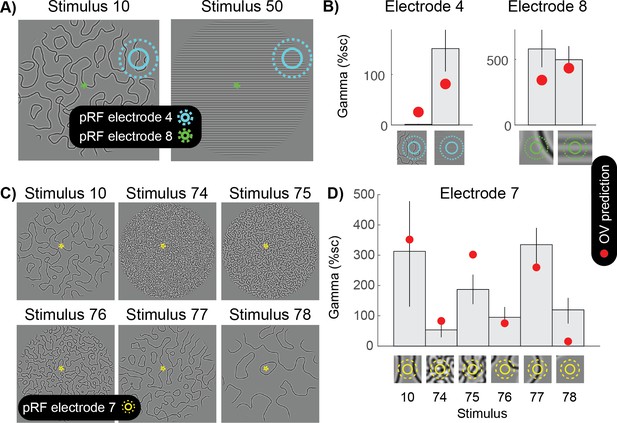
Grating-like features in the pRF strongly drive gamma oscillations.
(A) The population receptive fields (pRF) of two electrodes are overlaid on two different curved patterns (stimulus 10 and 50). Electrode four has a large pRF, while electrode eight has a very small pRF. (B) The left panel shows that for electrode 4, the OV model predicts a small response for the curved lines and a large gamma response for the grating pattern (red dots). As predicted, there is a small gamma response for the curved lines and a large response for the grating stimulus. Blue circles on the bottom zoom into the stimulus in the pRF. The right panel shows that for electrode 8, the OV model predicts a similar response for the image with curved lines and the image with a grating. As predicted, there is a large gamma response for the curved lines and a large response for the grating stimulus. Green circles on the bottom zoom into the stimulus in the pRF and this shows that from the curved lines, only a relatively straight line falls in the pRF. (C) Six different images with curves differing in sparseness (stimulus 10, 74, 75, 75, 76, 77 and 78). The population receptive field (pRF) of electrode seven is overlaid with one and two standard deviations (solid yellow and dotted yellow). (D) The OV model predicts the largest response when a grating-like feature hits the pRF (red dots). As predicted, the largest gamma responses are observed when the pRF contains grating-like features. Yellow circles on the bottom zoom into the pRF content of each of the stimuli. Error bars display the 68% confidence interval (across bootstraps), and the close up of image in the pRF show the outline of the pRF at 1 and 2 standard deviations (straight and dashed). Code to reproduce this figure can be found on GitHub (Hermes, 2019).

OV and SOC model predictions for images of natural scenes.
(A) The OV and SOC outputs are plotted for a set of gray-scale photographs of scenes, with model parameters from electrode 3. The units are in percent signal change, as in Figures 3 and 6. Each gray dot is the output of the two models for one image. The red dots are the model outputs for grating stimuli of varying contrast. The cluster of red dots at 100% contrast displays high-contrast gratings of different orientations (stimuli 39–46). The green and blue dots correspond to two images with large OV and SOC outputs, respectively. The right panels show these two images with the electrode pRF location superimposed (1 and 2 SDs). Natural image 1, with a high OV output, has image features in the pRF that look like a grating. The OV output to images of natural scenes are much lower than the responses to high contrast gratings. (B) Same as panel A, but for electrode 8, including a zoom into the pRF location. Code to reproduce this figure can be found on GitHub (Hermes, 2019).
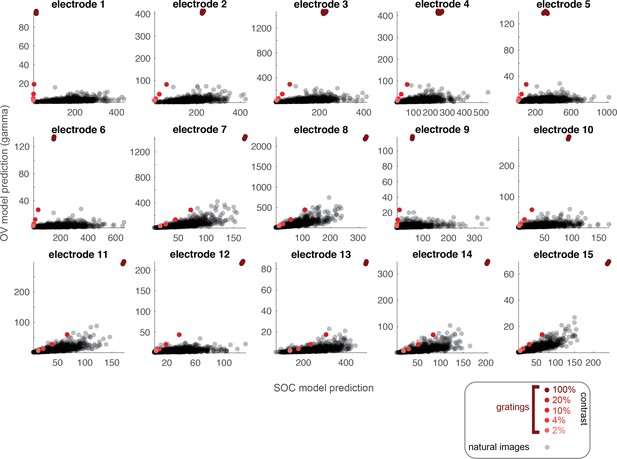
OV and SOC model predictions for images of natural scenes for all electrodes.
The OV and SOC outputs are calculated for a set of gray-scale photographs of scenes, with model parameters from each electrode. The units are in percent signal change. Each gray dot is the output of the two models for one image. The red dots are the model outputs for grating stimuli of varying contrast. The cluster of red dots at 100% contrast displays high-contrast gratings of different orientations (stimuli 39–46).

Matlab code.
https://doi.org/10.7554/eLife.47035.027
Output to simulate rank order statistic.
We simulated an experiment 1,000 times. In each case, there are 5 stimuli that drive systematic responses (amplitudes of 1, 2, 3, 4, and 5) and 45 stimuli that evoke responses centered at 0 (left panel). The scatter plot shows that the model fit is good. This is reflected by a high coefficient of determination (‘cod data’, blue); however, based on the rank ordered data points, the cod is poor, usually negative (‘cod ranks’, red).
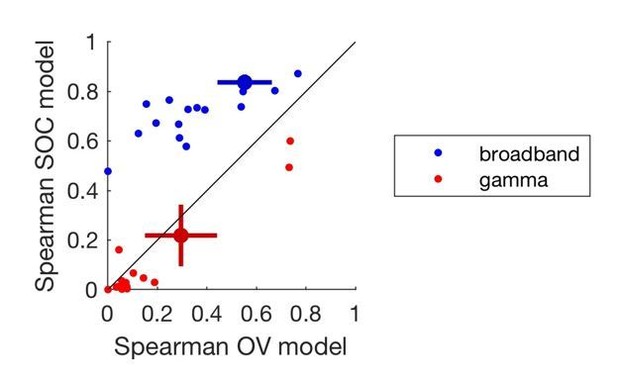
OV and SOC model performance on broadband and gamma power.
In this plot, model performance was calculated by the squared Spearman correlation. The x-axis shows the model performance of the OV model fit to the gamma power (red) and broadband power (blue). The y-axis shows the model performance of the SOC model fit to the gamma power (red) and broadband power (blue). The small dots show the performance for individual electrodes and the large dot indicates the mean +/- two times the standard error.
Tables
Variance explained by different models (coefficient of determination).
https://doi.org/10.7554/eLife.47035.020| Data | Model | ||
|---|---|---|---|
| Mean | SOC | OV | |
| Broadband | 41% | 80% | 24% |
| Gamma | 26% | 62% | 75% |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.47035.025





