Balancing model-based and memory-free action selection under competitive pressure
- University of Oregon, United States
Figures
Figure 1
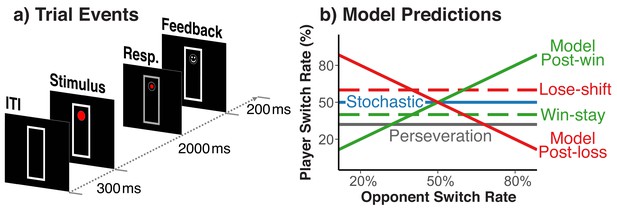
Trial events and theoretically possible switch-rate patterns.
(a) Sequence of trial events and response rules in the fox/rabbit paradigm. (b) Idealized predictions of how difference choice strategies and biases are expressed in the player’s switch rate. Choices based on an internal model of the opponent, lead to a positive relationship.
Figure 2 with 4 supplements
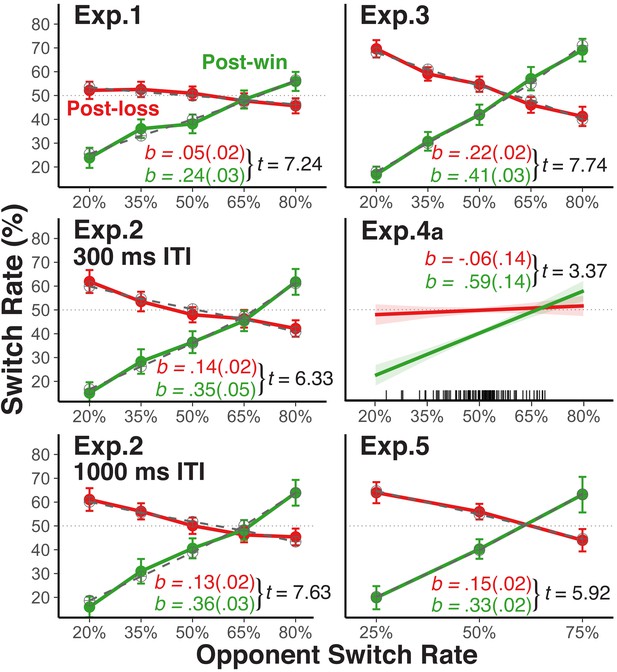
Player's average switch rates as a function of opponents' switch rates.
Average empirical switch rates for post-win and post-loss trials as a function of the simulated opponents’ switch rates for Experiment 1, 2, 3, and five and the average switch rate of each human opponent in Experiment 4a (tick marks on the x-axis indicate individual average switch rates). The dashed lines for Experiment 1, 2, 3, and 5 show the predictions of the theoretical choice model applied to the group average data (see sections Modeling Choice Behavior and Modeling Results). Error bars represent 95% within-subject confidence intervals. For the analyses, we regressed the player’s switch rate on the opponent’s switch rates, the win-loss contrast, and the interaction between these two predictors after reversing the labels of the opponents’ switch rate predictor for post-loss trials (see section Analytic Strategy for Testing Main Prediction). As a test of these interactions, we show the corresponding t-values (SE): the unstandardized slope coefficients (SE; green = post win, red = post loss) were derived from separate analyses for post-win and post-loss trials.
Figure 2—figure supplement 1
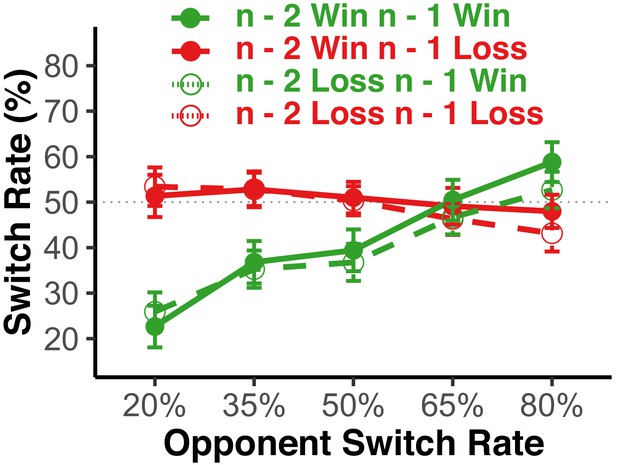
Are feedback effects temporary?
Our model assumes that the effect of loss-feedback does not eliminate the model of the opponent, but rather depresses it temporarily. Thus, we should expect that win-loss feedback has a large effect on the next-trial choice, and either no, or only a small effect thereafter. The figure shows for Experiment 1 the switch-rate function from Figure 2, but further conditioned on the trial n-2 win-loss feedback. As apparent, choice behavior is dominated by the effect of trial n-1 feedback. Error bars show 95% within-subject confidence intervals. There was small additional effect of trial n-2 feedback, such that model-based behavior was strengthened following two consecutive wins and stochastic behavior was strengthened following two loss trials (i.e., after two win-trial in a row, the switch-rate function slope becomes more positive, after two loss-trials the function becomes more shallow). Analyzing these data with an ANOVA with the factors trial n-2 and trial n-1 feedback as well as a linear contrast for the opponent switch-rate factor, revealed a strong n-1 feedback x switch-rate interaction, F(1,51)=58.45, p<0.001, eta2 = 0.53, and a much weaker, but still reliable n-2 feedback x switch-rate interaction, F(1,51)=15.02, p<0.001, eta2 = 0.23, and no three-way interaction, F(1,51)=.25, p=0.91. The results from the remaining experiments were similar to this pattern, and if anything, showed slightly weaker n-2 feedback effects than in Experiment 1. The fact that there was a small, cumulative effect of trial n-2 feedback indicates some degree of adaptation to consistent win or loss feedback contingencies. Yet, the fact that choices are mainly dominated by trial n-1 feedback indicates quick recovery of the last-used model representation following a subsequent win.
Figure 2—figure supplement 2
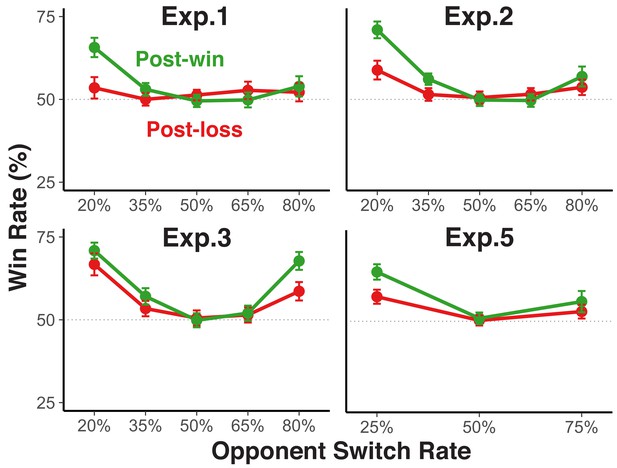
Rate of winning as a function of opponent switch rate and n-1 wins/losses.
Model-based behavior can be useful only when the opponent exhibits some degree of regularity. Therefore, we expect that participants show a greater success rate both after win than after loss feedback and when the opponent’s switch rate deviates from chance (p=0.5). This figure shows rate of winning as a function of n-1 wins versus losses and opponents’ switch rate across all experiments with simulated opponents; results for Experiment 2 are collapsed across the two ITI conditions, which showed almost identical patterns. Error bars indicate 95% within-subject confidence intervals. The results confirm expectations: The success rate followed a right-tilted, U-curved function with the most wins for the lowest switch rate, followed by the highest switch rate, and no above-chance success for the mid-range switch rates. Most importantly, this pattern was much more robust for post-win than for post-loss trials. The fact that rate of winning was highest for the opponent with the lowest switch rate, in particular after win trials is consistent with the fact that participants showed a greater tendency for model-based behavior when it required them to engage in low rather than high rates of switching. Within each experiment, the main effect of n-1 wins versus n-1 losses was highly significant (all Fs >= 24.5, p<0.001), as was the interaction between this factor and the quadratic trend for opponent switch rates (all Fs >= 10.77, p=0.003).
Figure 2—figure supplement 3
Analysis of action choices.
Traditionally, when analyzing choice behavior in experimental games, the focus is on the how players choose between different options. Given that our behavioral signature for model-based and stochastic behavior was based on the rate of switching between action choices, we focused on the rate of switching between options as our primary dependent variable. To ensure that we are not missing important results by only focusing on switch rate, we also examined for all experiments the allocation of choices between the ‘freeze’ and the ‘run’ option (or ‘up’ and ‘down’ for Experiment 3), as well as the degree to which choices were affected by our key independent variables (post-win/post-loss and opponent switch rate). Across all experiments, the choices were fairly evenly distributed (i.e., close to 50% for either option). The independent variables had at best only very small effects that were not consistent across experiments. This figure supplement shows example results from Experiment 1; the pattern for the remaining experiments is very similar. Thus, there are no obvious results in the pattern of action choices that would qualify the conclusions form the switch-rate data.
Figure 2—figure supplement 4
Switch rates when competing versus not competing.
The fox-rabbit task is a variant of the voluntary task-switching task, which is a standard paradigm for studying the ability to control selection of action rules in the absence of external prompts (Arrington and Logan, 2004). The most important result in this paradigm is a strong tendency to perseverate the last task/rule (i.e., a switch rate around 30%). In the standard paradigm, subjects are instructed to select tasks as randomly as possible. In contrast, in the fox-rabbit task, the competitive situation in combination with the informative, trial-by-trial feedback should provide an actual incentive to behave unpredictably. Therefore, it is useful to compare performance in the fox-rabbit task to the standard results from the voluntary switching paradigm. The contrast between the competitive situation in Experiment 4a and the non-competitive, but otherwise identical situation in Experiment 4b, allows such a comparison. As apparent, in the control experiment, switch rates were similar to results from the standard voluntary-switching situation and showed no robust feedback effect. In contrast, the competitive situation showed both larger switch rates and a strong win-stay/lose-shift bias (see also Figure 2). The fact that different processes occur in the competitive compared to the non-competitive situation is also apparent form the fact that average RTs in the first are much larger than in the latter (competitive: mean RT = 892 ms, SD = 118; non-competitive: mean RT = 577 ms, SD = 133) at comparable error rates (competitive: mean errors = 5.52%, SD = 1.40; non-competitive: mean errors = 6.80%, SD = 2.21). These results indicate that the competitive situation prompts participants to counter the perseveration bias, albeit at the cost of much longer RTs. This time cost probably reflects the use of the model of the opponent and active processing of the informative feedback--which in turn is likely to introduce the win-stay/lose-shift bias.
Figure 3
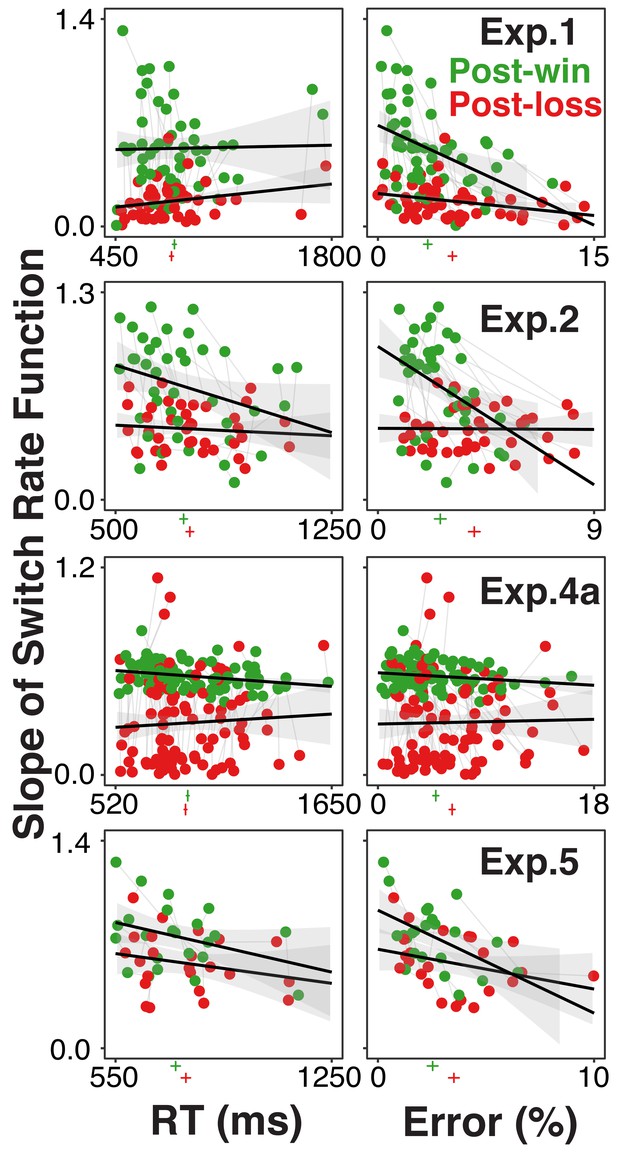
Individual participants’ degree of model-based choice (indicated by slopes of switch rate functions) in relationship to RTs and errors, separately for post-win (green) and post-loss (red) trials, and for each experiment using the rule-selection paradigm.
Each participant is represented both in the post-win and the post-loss condition. The green and red vertical lines below the x-axis of each graph indicate average RTs and error rates, the horizontal lines indicate 95% within-subject confidence intervals. If the increase of choice stochasticity between post-win and post-loss trials were due to greater, general information-processing noise, then the win/loss-related decrease in lopes of the switch rate functions would be accompanied by consistent increases in RTs and/or error rates.
Figure 4 with 2 supplements
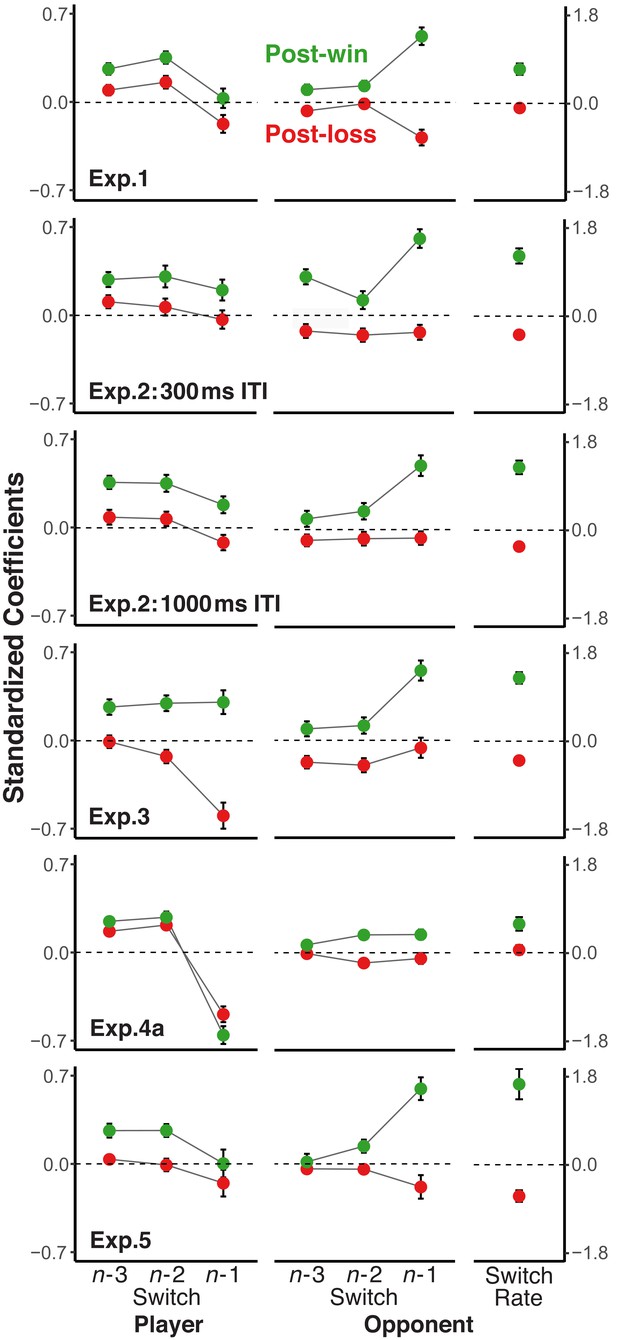
Standardized coefficients from multi-level logistic regression models predicting the trial n switch/no-switch choice on the basis of players’ and opponents’ switch/repeat choices on trials n-1 to n-3 and the opponents’ overall switch rate.
Error bars are standard errors around the coefficients. To focus on the difference in the strength of relationships rather than their sign, the labels for all opponent predictors were reversed for post-loss trials (see section Analytic Strategy for Testing Main Prediction). In addition, we also reversed the labels for all player-related predictors with a win/loss switch in sign. For a statistical test of the size difference between post-win and post-loss coefficients, all history/context variables were included into one model together with the post-win/post-loss contrast and the interaction between this contrast and each of the history/context predictors. Significance levels of the interaction terms are indicated in the figure,<0.05, *<0.01, ***<0.001.
Figure 4—figure supplement 1
History analysis with signed action choices.
Our main analyses to test the win/loss difference in the strength of the relationships between history/context and current choices involved selectively reversing labels of some of the predictors (see Figure 4). This figure supplement shows the, original, signed coefficients. For the opponent-related predictors, coefficients were generally positive following win feedback and negative, albeit smaller in size, following loss feedback. For player-related effects, the strength of the effects was also stronger following win than following loss trials, but the signs of the coefficients were less consistent than for the opponent-related predictors. Generally, these results are consistent with the conclusion that loss-feedback dampens the influence of the recent task context in general, not just as it relates to the opponents’ overall strategy.
Figure 4—figure supplement 2
Alternative analysis of history effects.
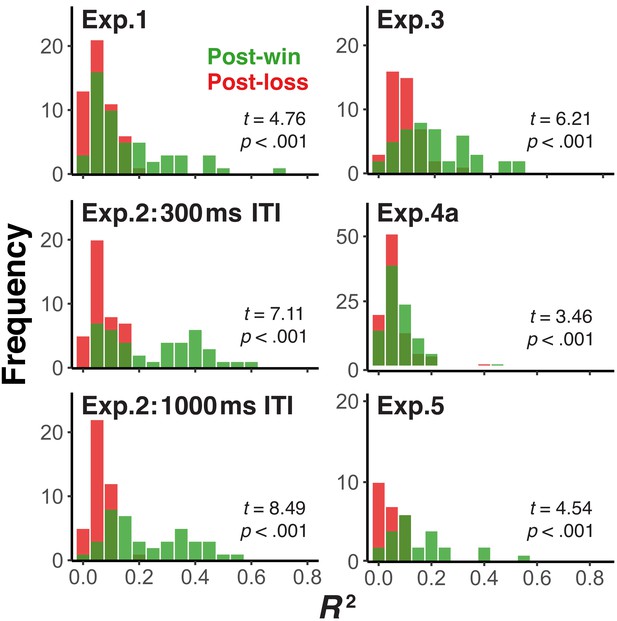
Aside from history analyses presented in Figure 4, we also conducted a more straightforward assessment of the effect of history on switch/repeat choices that did not require selective recoding of predictors. Specifically, we performed individual, logistic regression analyses for each subject, and separately for post-win and post-loss trials. Given that the effect of overall switch context was already demonstrated in our initial analyses (see Figure 2), we only included here the players’ and the opponents’ trial n-1 to n-3 switch/repeat choices as predictors. This figure supplement shows for each experiment the histograms of Cox and Snell pseudo R2-square scores from logistic regression models fitted within subjects (dark green shading indicates overlapping regions of the distributions). The difference in fit scores between post-win/loss was tested via t-test after converting R2 values into z-score (Cox, 2018). As apparent, post-win distributions were in all cases significantly farther to the right than post-loss distributions. Thus, these analyses confirm that following wins, switch/no-switch decisions are overall more dependent on history than post-loss decisions.
Figure 5 with 3 supplements
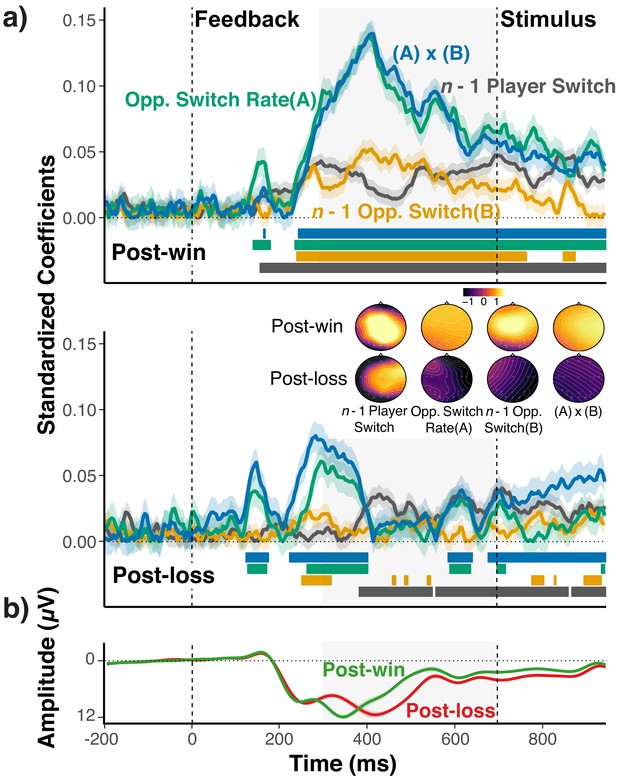
EEG-Analysis of choice-relevant information after wins and losses.
(a) Standardized coefficients from multi-level regression models relating EEG activity at Fz and Cz electrodes to the opponents’ overall switch rate (A), the n-1 opponent switch/no-switch choice (B), the n-1 players’ switch/no-switch choice, and the interaction between (A) and (B) for each time point and separately for post-win (upper panel) and post-loss (lower panel) trials. Shaded areas around each line indicate within-subject standard errors around coefficients. As coefficients for opponent-related predictors showed a marked, win/loss flip in sign, we again reversed the label of the post-loss predictors (see section Strategy for Testing Main Prediction and Figures 2 and 3; for signed coefficients, see Figure 5—figure supplement 2). For illustrative purposes, colored bars at the bottom of each panel indicate the time points for which the coefficients were significantly different from zero (p<0.05, uncorrected). See text for statistical tests of the predicted differences between coefficients for post-win and post-loss trials. The insert shows the topographic maps of coefficients that result from fitting the same model for each electrode separately. Prior to rendering, coefficients were z-scored across all coefficients and conditions to achieve a common scale. (b) Average ERPs for post-win and post-loss trials, showing the standard, feedback-related wave form, including the feedback-related negativity (i.e., the early, negative deflection on post-loss trials). Detailed ERP results are presented in Figure 5—figure supplement 3.
Figure 5—figure supplement 1
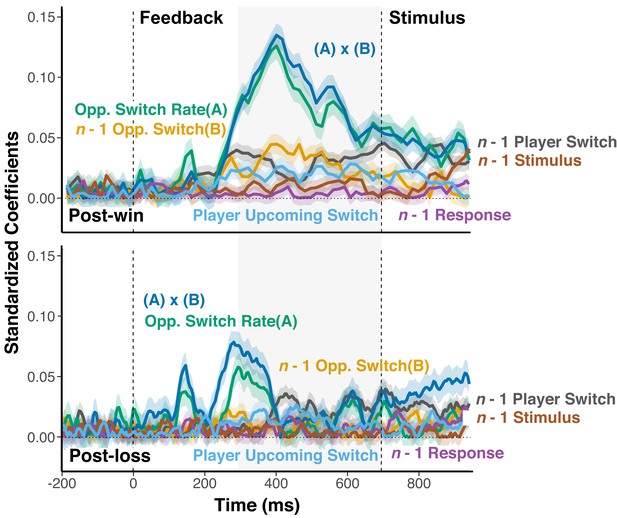
Controlling for Upcoming Switch and n-1 Stimulus/Response Positions.
The supplement shows the results of the same analysis as in Figure 5, but adding potentially relevant control variables. It is possible that the feedback-related differences for the history/context coefficients shown in Figure 5 are due to the fact that feedback affects the probability of an upcoming switch. For example, the EEG effects may reflect preparatory processes associated with an upcoming switch, such as the allocation of effort. As shown, information about the upcoming switch/no-switch choice was reliably reflected in the EEG signal (t = 2.67). However, different from the history/context variables, the coefficient associated with the upcoming choice was not affected by post-win/-loss feedback (t = 0.68). This pattern is consistent with (Donahue et al., 2013) who have found that frontal and parietal neurons code past choices in a feedback-contingent manner, but represent the upcoming choice in a manner that is not conditioned on previous-trial feedback. As additional control analyses, we also added n-1 stimulus position and response locations to ensure that none of the effects of interest are driven by such lower-level effects. As evident, the overall pattern of history/context effects remains the same when controlling these potential influences.
Figure 5—figure supplement 2
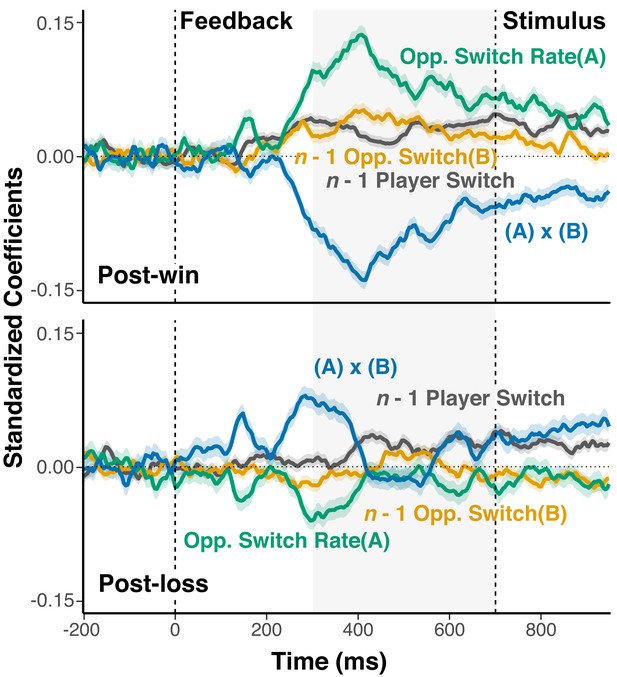
Signed predictors.
In Figure 5, we had reversed the labels for the opponent-related predictors because our predictions referred to the amount of information about the competitive context, not how exactly that information is expressed in the EEG signal. This supplement presents the same analyses as in Figure 5, however plotted using the original predictors (i.e., without reversing labels on post-loss trials). Results reveal a clear distinction between post-loss and post-win signals. For all opponent-related predictors, the effect on the EEG signal was not only reduced following losses, it was also flipped in sign relative to post-win trials. Note, that opponents’ local and global switch behavior has very different implications for the subject’s behavior depending on whether one is currently winning or losing (e.g., see Figure 1b). Thus, one might speculate that this flip in sign is indicative of the win/loss-contingent difference in interpretation (or behavioral implication) of the information provided through the opponent.
Figure 5—figure supplement 3
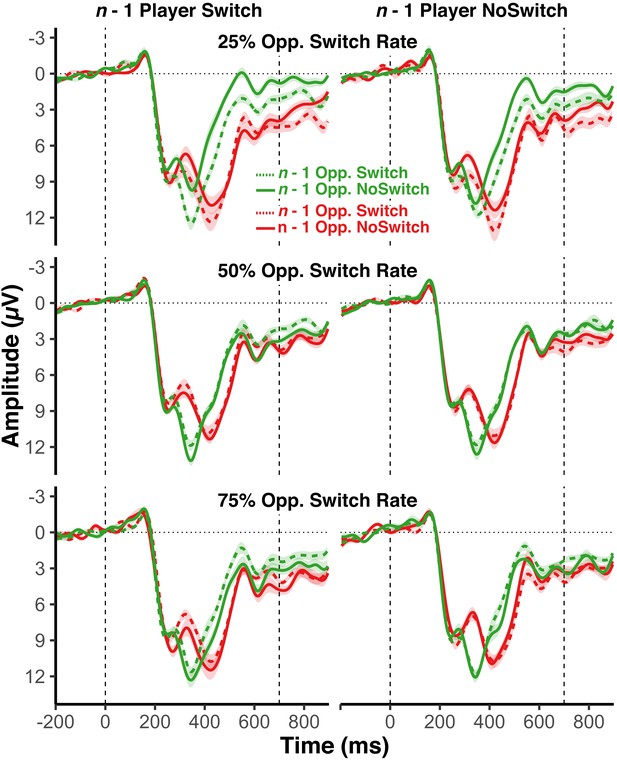
Event-related potentials.
The supplement shows event related potentials (ERPs) in terms of grand average EEG activity for electrodes Fz and Cz grouped by all factors used in the EEG analysis: the opponent’s overall switch rate (20,50,75%), the n-1 opponent switch/no-switch choice, and the n-1 player’s switch/no-switch choice. The EEG signal was low-pass filtered (Butterworth, 25 Hz), time-locked to the onset of feedback, and subtracted from the average across the 200 ms baseline period prior to the feedback signal. The shaded area indicates within-subject 95% confidence intervals around the average signal. Following the feedback (200 to 300 ms after the onset), we observed a typical feedback-related negativity (FRN), with a peak that was more negative for loss feedback compared to win feedback. Consistent with the results of the main analysis, the FRN was affected by the combination of feedback and context variables: The FRN amplitude was most negative for unexpected opponent switch or repeat choices, that is for opponent switch choices for 25% switch-rate opponents and (to a lesser degree) for repeat choices when facing 75% switch-rate opponents). The fact that we generally find a larger negativity during the typical FRN time range (200 to 300 ms after the onset of feedback) following loss trials is consistent with a negative prediction error account.
Figure 6
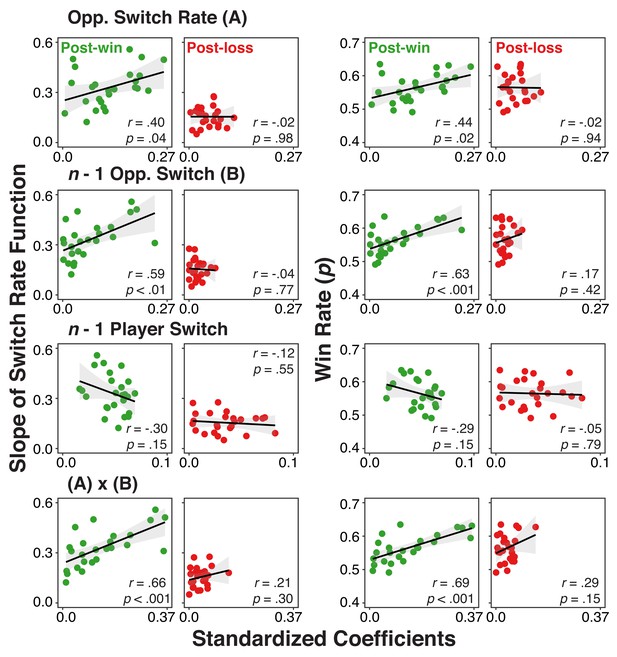
Individual difference correlations between neural-level representation of history/context variables and both use of the model and rate of winning.
Correlations between individuals’ standardized coefficients from the multi-level regression analysis relating the EEG signal to the different history/context variables and 1) their slopes for the switch rate functions (left two columns) or 2) their overall win rate (right two columns) separately for post-win and post-loss conditions. Coefficients were obtained by fitting models with the EEG signals averaged over a 300–700 ms interval of the post-feedback period (the shaded interval in Figure 5).
Author response image 1
Tables
Table 1
Parameter estimates and 95% confidence intervals from fitting the choice model to group average and individual data from Experiments 1, 2, 3, and 5.
https://doi.org/10.7554/eLife.48810.009| Fitting group averages | Fitting individuals’ Data | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameters | ms | sm | pe | ss | R2 | ms | sm | pe | ss |
| Simulated Opp. | |||||||||
| Exp. 1 | 0.48 ± 0.10 | −0.38 ± 0.09 | 0.21 ± 0.06 | 0.20 ± 0.06 | 0.975 | 0.61 ± 0.19 | −0.50 ± 0.16 | 0.24 ± 0.14 | 0.22 ± 0.11 |
| Exp. 2, 300 ms | 0.74 ± 0.12 | −0.47 ± 0.15 | 0.28 ± 0.07 | 0.30 ± 0.07 | 0.988 | 0.96 ± 0.26 | −0.66 ± 0.24 | 0.34 ± 0.10 | 0.36 ± 0.14 |
| Exp. 2, 1000 ms | 0.74 ± 0.13 | −0.49 ± 0.17 | 0.19 ± 0.08 | 0.26 ± 0.08 | 0.984 | 0.93 ± 0.24 | −0.67 ± 0.21 | 0.25 ± 0.11 | 0.33 ± 0.13 |
| Exp. 3 | 0.86 ± 0.11 | −0.44 ± 0.14 | 0.07 ± 0.04 | 0.24 ± 0.06 | 0.993 | 1.13 ± 0.28 | −0.68 ± 0.23 | 0.11 ± 0.10 | 0.29 ± 0.11 |
| Exp. 5 | 0.87 ± 0.17 | −0.50 ± 0.21 | 0.11 ± 0.09 | 0.30 ± 0.09 | 0.998 | 1.10 ± 0.39 | −0.71 ± 0.30 | 0.16 ± 0.10 | 0.36 ± 0.24 |
| Human Dyads | |||||||||
| Exp. 4a | 0.16 ± 0.10 | −0.14 ± 0.13 | 0.11 ± 0.9 | 0.31 ± 0.9 | |||||
-
Note. ms = model strength, sm = suppression of model (strategy mix), pe = perseveration effect, ss = win stay/lose-shift tendency. For Experiment 2, fits are reported separately for the 300 ms and the 1000 ms ITI condition. Fits for individual subjects in Experiments 1, 2, 3, and five are on the basis of each subject’s condition averages. For Experiment 4a, we report parameters resulting from modeling individuals’ trial-by-trial choices.
Table 2
Using parameter estimates from the choice-model fitted to individual’s condition means to predict individual’s competitive success.
https://doi.org/10.7554/eLife.48810.010| B | SE | t-value | |
|---|---|---|---|
| intercept | 0.504 | ||
| ms | 0.086 | 0.007 | 12.31 |
| sm | 0. 064 | 0.008 | 8.03 |
| abs(pe) | −0.016 | 0.006 | −2.56 |
| abs(ss) | −0.001 | 0.001 | −0.10 |
-
Note. Shown are fixed-effect coefficients (b), the standard error around the coefficients (SE), and the associated t-value. Experiment was coded as a random grouping factor. Absolute values for the pe and the wl effect were used to account for biases in either direction. Note, that the more negative the sm parameter, the greater the suppression of model-based choice on post-loss trials. Thus, a positive coefficient in this analysis indicates that less suppression leads to higher earnings.
Table 3
Using parameter estimates from the choice-model fitted to individual’s trial-by-trial data to predict the proportion of win trials (n = 94) in Experiment 4a.
https://doi.org/10.7554/eLife.48810.011| B | SE | t-value | |
|---|---|---|---|
| intercept | −0.530 | 0.005 | |
| ms | 0.043 | 0.015 | 2.91 |
| sm | 0. 034 | 0.012 | 2.97 |
| abs(pe) | −0.080 | 0.019 | −4.11 |
| abs(ss) | 0.062 | 0.014 | 4.48 |
-
Note. Shown are the unstandardized regression coefficients (b), the standard error around the coefficients (se), and the associated t and p values. Note, that the more negative the sm parameter, the greater the suppression of model-based choice on post-loss trials. Thus, a positive coefficient in this analysis indicates that less suppression leads to higher earnings.
Table 4
Coefficients from the PPI analysis predicting upcoming choices using residuals of MLM regression model for post-win and post-loss trials.
https://doi.org/10.7554/eLife.48810.020| Post-win | Post-loss | |||||
|---|---|---|---|---|---|---|
| B | SE | z-value | B | SE | z-value | |
| Opponent Switch Rate (A) | 1.44 | .047 | 31.15 | −0.62 | 0.046 | −13.47 |
| n-1 Opponent Switch (B) | 0.76 | 0.038 | 19.96 | −0.07 | 0.034 | −1.99 |
| n-1 Player Switch (C) | 0.15 | 0.033 | 4.57 | −0.23 | 0.033 | −6.80 |
| A x B | −0.17 | 0.068 | −2.57 | 0.08 | 0.061 | 1.37 |
| Residual EEG (D) | 0.20 | 0.03 | 6.39 | 0.07 | 0.04 | 2.05 |
| D x A | 0.11 | 0.05 | 2.26 | −0.11 | 0.05 | −2.37 |
| D x B | −0.13 | 0.04 | −3.31 | −0.03 | 0.03 | −0.95 |
| D x C | −0.11 | 0.03 | −3.36 | −0.01 | 0.03 | −0.36 |
| D x A x B | −0.06 | 0.07 | −0.89 | 0.08 | 0.06 | 1.37 |
-
Note. Shown are the unstandardized regression coefficients (B), the standard error around the coefficients (SE), and the associated z values. Bolded values indicate significant effects (i.e., z-values > 2).
Author response table 1
Absolute coefficients from the MLM regression predicting trial-to-trial EEG signals with additional control predictors.
https://doi.org/10.7554/eLife.48810.023| Post-win | Post-loss | ||||||
|---|---|---|---|---|---|---|---|
| Model | b | se | t-value | b | se | t-value | |
| Original | Opponent Switch Rate(A) | .120 | .00 | 11.04 | -.033 | .012 | -2.80 |
| n-1 Opponent Switch (B) | .062 | .018 | 5.66 | <-.001 | .008 | -0.05 | |
| n-1 Player Switch | .048 | .007 | 6.32 | .003 | .008 | 4.06 | |
| (A) x (B) | -.134 | .010 | -12.11 | .028 | .012 | 2.15 | |
| No interaction | Opponent Switch Rate | .038 | .014 | 2.74 | -.011 | .015 | -.743 |
| n-1 Opponent Switch | .039 | .011 | 3.66 | <.001 | .010 | .083 | |
| n-1Player Switch | .049 | .009 | 5.24 | .010 | .009 | 3.27 | |
| n-1 Player switch | Opponent Switch Rate(A) | .184 | .162 | 14.68 | -.265 | .015 | -1.79 |
| n-1 Opponent Switch (B) | .049 | .013 | 5.61 | <.001 | .008 | .076 | |
| n-1 Player Switch (C) | .041 | .001 | 5.96 | .033 | .008 | 4.10 | |
| (A) x (B) | -.110 | .011 | -10.47 | .025 | .012 | 2.05 | |
| (A) x (C) | -.102 | <.001 | -10.93 | .001 | .011 | -.89 | |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.48810.022
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Balancing model-based and memory-free action selection under competitive pressure
eLife 8:e48810.
https://doi.org/10.7554/eLife.48810
