The computation of directional selectivity in the Drosophila OFF motion pathway
- Howard Hughes Medical Institute, United States
Figures
Figure 1
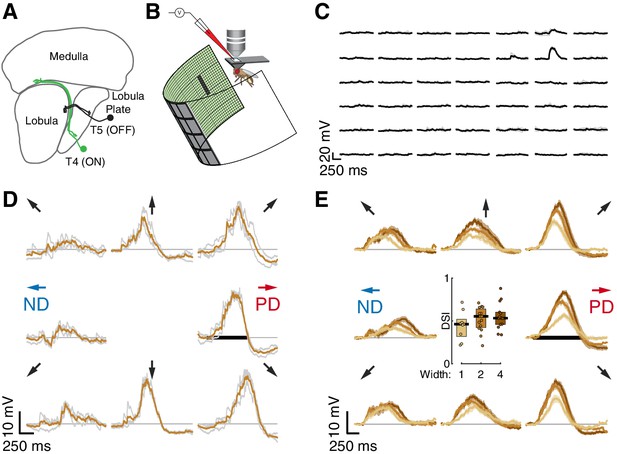
Whole-cell recordings of T5 neurons show small-field, directionally selective responses.
(A) Schematic of the Drosophila visual system with an example T4 (ON) and T5 (OFF) neuron. (B) Schematic of experimental setup. Whole-cell recordings were targeted to soma of GFP-labeled T5 neurons. (C) Responses to 200 ms OFF square flashes (~11°×11°) from an example cell. Each subplot shows the response from a different location on the LED display, which subtended 216° (azimuth) ×72° (elevation) of the visual space. Individual repeats in gray (n = 3 trials), mean in black. (D) Responses from the same cell in (C) to a 2-pixel wide dark bar (2 × 9 LEDs,~4.5°×20.25°) moving in eight directions at 28°/s (80 ms/pixel) through the center of the receptive field. Repeats in gray (n = 3 trials), mean in brown. Black horizontal bar indicates the stimulus duration. PD indicates the Preferred Direction and ND indicates the Null Direction. (E) Baseline-subtracted responses (n = 17 cells) to a moving bar of width 1, 2, and 4 pixels (2.25°, 4.5°, and 9°), aligned to the PD of each cell (mean ± SEM). Arrows represent the direction of stimulus motion. Black horizontal bar indicates stimulus presentation. Inset: DSI = [PDmax – NDmax]/PDmax for moving bar responses (n = 9, 15, 14 cells).
Figure 2 with 1 supplement
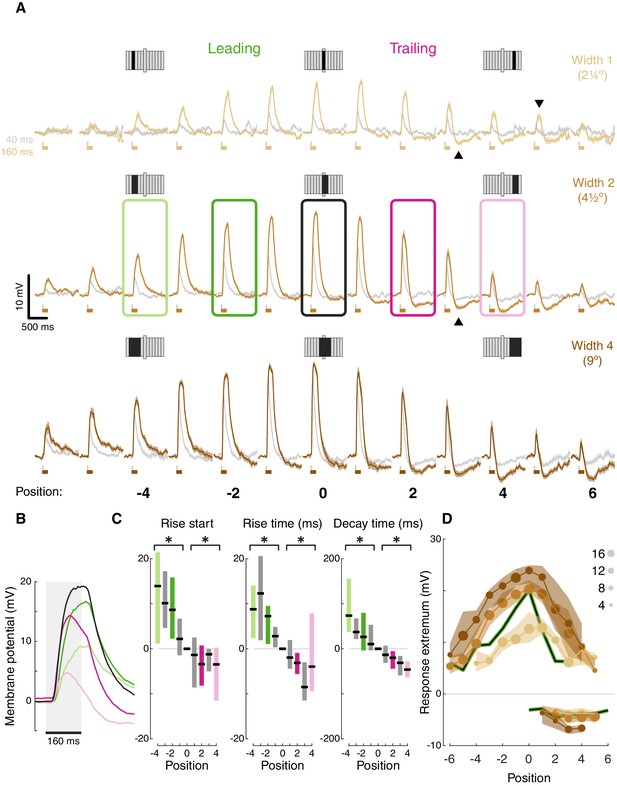
T5 receptive field is comprised of spatially offset depolarization and hyperpolarization.
(A) Averaged, baseline-subtracted responses (mean ± SEM) to bar flash stimulus at the indicated positions (numbered below, examples schematized above) along the PD–ND axis of each cell (n = 17 cells) aligned to the central depolarizing position (=0, see Materials and methods for details). Responses to 40 ms flashes in gray; responses to 160 ms flashes are colored. Elongated bar in each stimulus schematic marks center position. Downwards arrowhead: example non-linearity in responses to stimuli of different durations. Upwards arrowhead: example non-linearity in hyperpolarization in response to stimuli of different durations. (B) Mean responses from indicated positions in (A) of width-2 bar flashes, aligned to stimulus presentation (gray rectangle). (C) Response rise start time (time to reach 10% of max), rise time (10%–50%), and decay time (80%–20%) for positions surrounding the receptive field center (calculated for 160 ms flashes of width-2 bars). Results presented as differences from the central position (* indicates significantly above/below zero for pooled positions from the leading/trailing side respectively, two-tailed t-test, p<0.05; n = 17 cells). (D) Maximum depolarizing and hyperpolarizing responses at each stimulus position for 160 ms bar flashes of all three widths. Dots correspond to median response (size indicates the number of cells for each position), shaded regions demarcate upper and lower quartiles. Superimposed black line represents the median T4 results for width 1 ON bars (Gruntman et al., 2018). See also Figure 2—figure supplement 1 for the T5 receptive field corrected for visual angle.
Figure 2—figure supplement 1
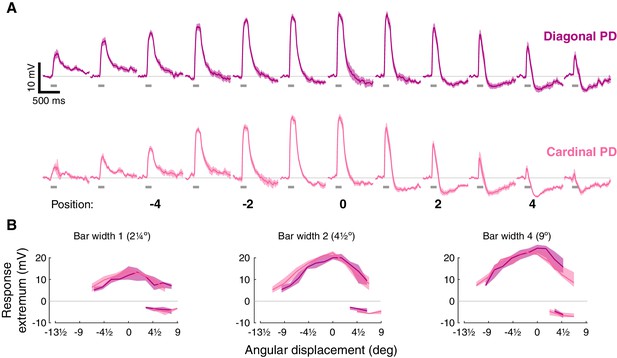
T5 receptive field comparison between cells aligned to cardinal and diagonal preferred directions, corrected for approximate visual angle.
(A) Averaged, baseline-subtracted responses (mean ± SEM) to bar flash stimuli (width 4, 160 ms) at the indicated positions (numbered below) along the PD–ND axis of each cell (n = 12 cells for diagonal; n = 5 cells for cardinal) aligned to the center excitatory position. (B) Maximum depolarizing and hyperpolarizing responses at each stimulus position for 160 ms bar flashes of all three widths corrected for visual angle. Lines correspond to median responses; shaded regions demarcate upper and lower quartiles. Note that after correction the receptive fields for both groups are highly overlapping.
Figure 3 with 2 supplements
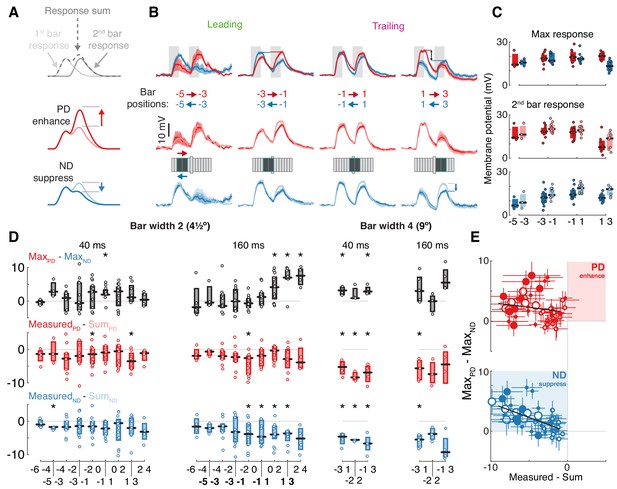
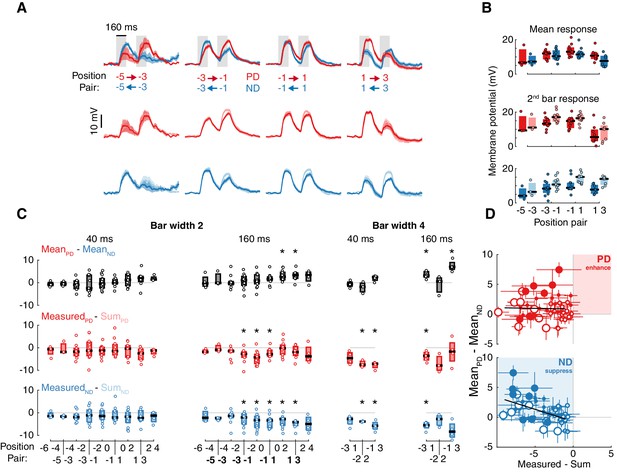
T5 neurons generate directional selectivity using ND suppression.
(A) Schematized responses to the elementary motion stimulus of sequential bar pair flashes. Response could be the sum of the responses to the individual flashes (top), could show preferred direction, PD, enhancement (middle) or null direction, ND, suppression (bottom). (B) Baseline-subtracted responses (mean ± SEM) to bar pair combinations presented at different positions along the PD–ND axis (n = 3,11,11,8 cells). Top: responses to PD and ND bar pairs. Middle: responses to PD bar pairs (same as top) with the temporally aligned sum of the responses to the component bar flashes in pink. Bottom: responses to ND bar pairs (same as top), sum of responses to component bar flashes in cyan. Stimulus presentation interval indicated with gray rectangles. Stimulus schematic shows positions of both bars (0 position depicted by elongated bar). (C) Boxplot summary of response maxima for (B) (same color conventions). Top: response maxima, Middle and Bottom: second bar maxima for measured and summed responses. (D) Boxplot summary of response maxima differences for all (non-overlapping) bar pair stimuli presented. Top: difference between PD and ND, positive value indicates a directionally selective response. Middle: difference between second bar response maxima for measured and summed PD responses. Positive value indicates PD enhancement. Bottom: same as middle, but for ND. Negative value indicates ND suppression (* indicates mean significantly differs from zero, unpaired t-test corrected for multiple comparisons by controlling for the false discovery rate with q = 0.075). Boldface positions are presented in (B) and (C). (E) Comparison of directional selectivity versus linearity of response for all presented bar pair combinations, including data from (D) and responses to overlapping positions (see Materials and methods). Each dot corresponds to the mean (of n ≥ 3 cells) response differences for each position pair (± SEM). Marker size indicates bar width (small for 2, large for 4-pixel wide), marker fill indicates duration (empty 40 ms, filled 160 ms). Results of linear regression in black (non-significant slope for MeasuredPD - SumPD vs. MaxPD - MaxND, [−0.402, 0.073], 95% confidence interval; significant slope for MeasuredND - SumND vs. MaxPD - MaxND, [−0.641,–0.301], 95% confidence interval). See also Figure 3—figure supplement 2 for more details of bar width four responses.
Figure 3—figure supplement 1
Evidence for ND suppression is robust to measurement type.
This figure shows the same analysis and results as in Figure 3, but summarized using response mean rather than peak. (A) Baseline-subtracted responses (mean ± SEM) to bar pair combinations presented at different positions along the PD–ND axis (same as in Figure 3). (B) Boxplot summary of response means for (A) (same color conventions). Top: response means, Middle and Bottom: second bar means for measured and summed responses. (C) Boxplot summary of differences in response means for all (non-overlapping) bar pair stimuli presented. Top: difference between PD and ND, positive value indicates a directionally selective response. Middle: difference between second bar response means for measured and summed PD responses. Positive value indicates PD enhancement. Bottom: same as middle, but for ND. Negative value indicates ND suppression (* indicates mean significantly differs from zero, unpaired t-test corrected for multiple comparisons by controlling for the false discovery rate with q = 0.075). Boldface positions are presented in (A and B). (D) Comparison of directional selectivity versus linearity of response for all presented bar pair combinations, including data from (C) and responses to overlapping positions (see Materials and methods). Each dot corresponds to the mean (of n ≥ 3 cells) response differences for each position pair (± SEM). Marker size indicates bar width (small for 2, large for 4-pixel wide), marker fill indicates duration (empty 40 ms, filled 160 ms). Results of linear regression in black (non-significant slope for MeasuredPD - SumPD vs. MeanPD - MeanND , [−0.25, 0.21], 95% confidence interval; significant slope for MeasuredND - SumND vs. MeanPD - MeanND ,. [−0.6,–0.21], 95% confidence interval).
Figure 3—figure supplement 2
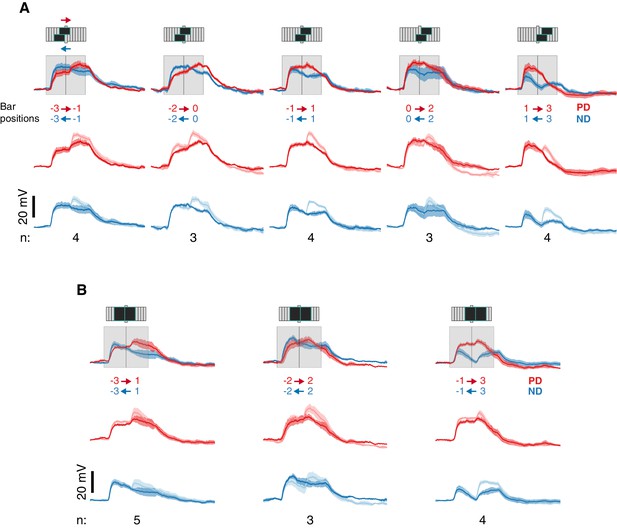
Apparent motion responses show evidence only for ND suppression even for larger stimuli.
(A) Same as Figure 3B for 4-pixel-wide (9°) apparent motion stimuli. Stimulus schematic depicts positional information only and are presented in a staggered manner to illustrate overlapping positions for these pairwise combinations. Numbers below each column indicate the number of cells for that pairwise comparison. (B) Same as (A), but for non-overlapping positions. Summary of these pairwise combinations is shown in Figure 3D. Every combination shows a clear sub-linearity in response to the second bar’s appearance (measured response is always close to or smaller than the summed response in the lighter color).
Figure 4 with 1 supplement
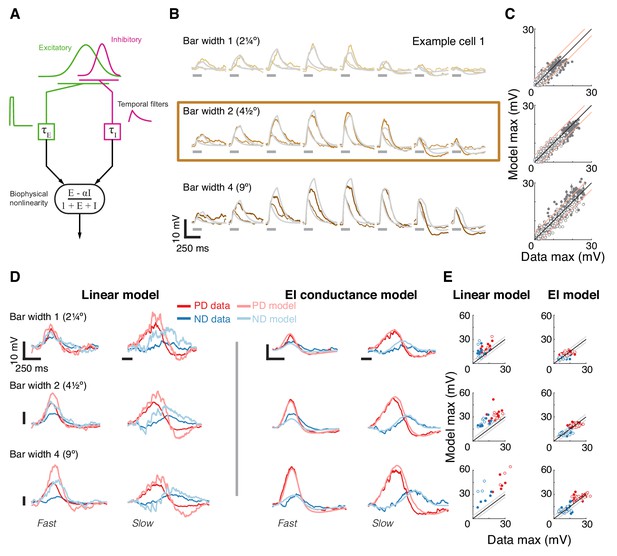
A conductance-based model quantitatively predicts directionally selective responses.
(A) T5 EI model schematic with fast spatially symmetric excitation and slow, trailing-side asymmetric inhibition. (B) Mean measured responses to single bar flashes of 3 widths and two flash durations at eight different positions (in colors) compared to predicted model responses (gray) from an example cell (same as Figure 1). Model parameters were optimized to each cell using only responses from bars of width 2 (brown frame). (C) Peak measured response compared to the peak of the predicted response for all bar flash stimuli from all cells and positions (empty marker denotes short duration flash, filled denotes long flashes). Each dot represents the mean peak response (for top 10 of 1000 optimization solutions for each cell, estimated by fit error), while vertical lines (most obscured by markers) represent maximal and minimal values of the peak responses. Diagonal lines surrounding the unity line denote + /- the upper quartile of the Mean Absolute Deviation (MAD) of responses to repeated presentation of the same stimuli (see Materials and methods). (D) Mean measured responses to moving bars of three widths and two speeds overlaid with predicted responses from linear (superposition of flash responses) and EI conductance model for same example cell and the same model parameters as in (B). Note scale change on voltage axis of linear predictions due to overestimation. (E) Peak measured responses compared to peak predicted responses from both linear and EI models for all moving bars (grouped by bar width). Plotting conventions as in C; except PD in red, ND in blue. Note consistent overestimation of linear model, which is exacerbated for larger stimuli. See also Figure 4—figure supplement 1 for distributions of individual cell measurement and EI model prediction responses.
Figure 4—figure supplement 1
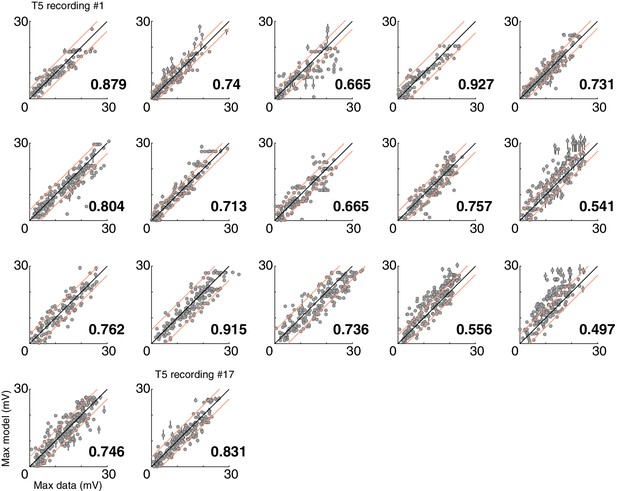
Reliability of model predictions across cells.
Each subplot shows peak measured responses compared to the peak model prediction responses for all the stimuli recorded for an individual cell. Plotting conventions are as in Figure 4C. The bolded value on the lower right of each plot is the proportion of model responses falling within the ‘MAD bounds’ (a measure of dispersion bases on the Mean Absolute Deviation of measured responses to the same stimulus).
Figure 5
Conductance-based model recapitulates responses to more complex spatial and temporal stimuli.
(A) Mean measured responses to fast (40 ms) and slow (160 ms) flashes of grating stimuli (dark and background brightness level) in different phases compared with model predictions (same example cell, same model parameters as in Figure 4B). Stimulus schematic above traces. In two phases, the expected relative contribution (bold >normal) of excitation and inhibition based on the position of the dark bars is denoted. (B) Peak measured response compared to peak predicted response, for flashes of all grating phases, grouped by flash duration. Plotting conventions as in Figure 4C (only results from cells with a cardinal PD-ND axis are shown; n = 5, see Materials and methods). (C) Mean measured responses to grating stimuli moving at two speeds (temporal frequency of 3.125 Hz and 0.78 Hz, 40 ms and 160 ms steps), with two different starting phases, compared to model prediction for the same example cell and model parameters as 4B. (D) As in (C), only from a different example cell. Note the difference in phase relations between PD and ND responses for cells in (C) and D). (E) Top: Fit amplitude values for measured response compared to the model predicted responses for all grating stimuli (see Materials and methods for details). Plotting conventions as in 4E. Bottom: fit phase values for measured responses compared to model prediction responses.
Figure 6 with 2 supplements
A conductance model relying on removal of excitatory input cannot recapitulate T5 responses.
(A) Mean measured responses to single bar flashes of two widths flashed for 160 ms at eight different positions from the same example cell as in Figure 4 (in colors) compared to predicted E+E- model responses (gray). Model parameters were optimized using only responses to bar width two flashes (brown frame). (B) Peak measured response compared to peak predicted response for bar flash stimuli from all cells and positions. Same conventions as in Figure 4, but only 160 ms flash responses are shown. The E+E- model overestimates the width 4 bar flash responses. (C) Traces: Mean measured responses from same example cell as in Figure 4 for slow moving bar stimuli overlaid with E+E- model predicted responses. Scatter plots: Peak measured responses compared to peak predicted responses from E+E- model for all moving bar responses across cells (grouped by bar width). Plotting conventions as in Figure 4. Note similar response magnitude for PD and ND stimuli; DSI comparison provided for the example cell and E+E- model. See also Figure 6—figure supplements 1 and 2 for E+E- model results from different optimization procedures.
Figure 6—figure supplement 1
E+E- model relying on removal of excitatory input cannot recapitulate T5 responses, even when optimized with bars of width 2 and 4.
(A) Mean measured responses to single bar flashes of two widths flashed for 160 ms at eight different positions from the same example cell as in Figure 4 (in colors) compared to predicted E+E- model responses (gray). Model parameters were optimized using responses to flashing bars of both widths (brown frame). (B) Peak measured response compared to peak predicted response for bar flash stimuli from all cells and positions. Same conventions as in Figure 6. Note the under-estimation of width-2 bar flashes (C) Traces: Mean measured responses from same example cell and same stimuli as in Figure 6 overlaid with E+E- model predicted responses. Scatter plots: Peak measured responses compared to peak predicted responses from E+E- model for all moving bars responses across cells (grouped by bar width). Plotting conventions as in Figure 6. Note similar response magnitude for PD and ND stimuli; DSI comparison provided for the example cell and E+E- model. (D) Mean measured responses to slow (160 ms) flashes of grating stimuli in different phases compared with model predictions (same example cell, same model parameters as in (A). Stimulus schematic above traces are same as in Figure 5A. (E) Peak measured response compared to peak predicted response, for flashes of all grating phases. Plotting conventions as in Figure 5B.
Figure 6—figure supplement 2
E+E- model relying on removal of excitatory input cannot recapitulate T5 responses, even when optimized with flashing and moving bars.
Same as Figure 6—figure supplement 1, but these results were generated using model parameters that were optimized using flashing and moving bars responses of width 2 (brown frame).
Figure 7
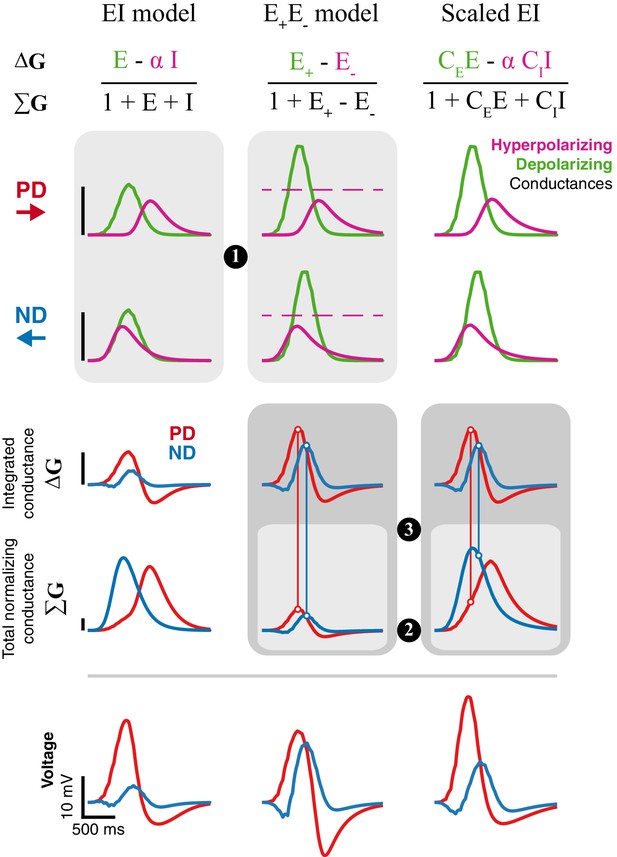
Inhibition is superior to removal of excitation for generating directional selectivity.
Each column presents responses from a different model version to a moving bar stimulus of width 2 with 80ms step duration: EI model from Figure 4, E+E- model from Figure 6, and a Scaled version of the EI model. Parameters for first and second column are the best fit (for each model, separately) for the example cell used in Figure 4 and 6. The Scaled EI model parameters were inherited from the E+E- model (see Materials and methods for details), with coefficients (CE, CI) required to match the depolarizing and hyperpolarizing conductances in the numerator of the E+E- model. First and second rows show the dynamics of the depolarizing and hyperpolarizing conductances in each model to PD and ND stimuli. The dashed line in the E+E- column represents the magnitude of (maximal value for E-, see Materials and methods). Third, fourth, and fifth rows show, respectively, the integrated conductance, the total conductance, and the voltage response of each model version. Circled numbers and shaded frames emphasize comparisons discussed in the Results. Scale bars are shared across columns and, for the top four rows, represent 0.5 normalizing conductance (Leak for EI and scaled EI, total stimulus-independent conductances for E+E-).
Figure 8
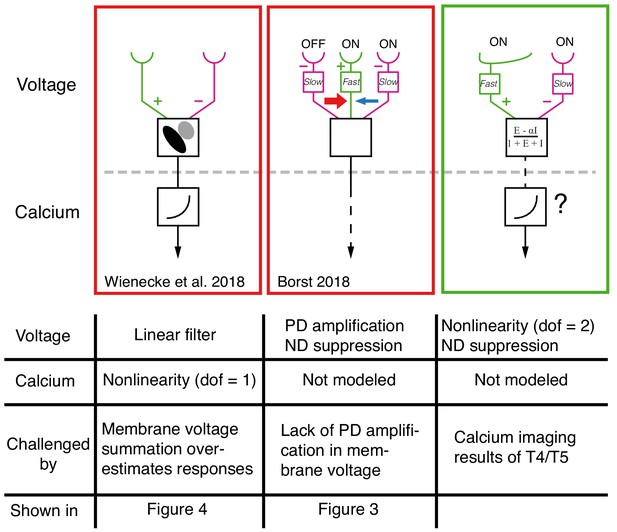
Comparison between current models for T4/T5 computation of directional selectivity.
One recent model class, represented here by the proposal of Wienecke et al. (2018) uses a tilted linear spatio-temporal filter to represent voltage responses, which are then followed by a nonlinear voltage-to-calcium transformation (1 degree of freedom, dof). Another current model class, represented here by the version from Borst (2018), proposes a three-arm model that uses a biophysical mechanism to generate PD amplification and ND suppression; the calcium transformation is not modeled. Both of these models cannot explain our T5 results. The specific results that challenge these proposals are detailed in the table below each model. The right column shows a unifying proposal in which our EI model implements a 2 dof nonlinearity (dofs represented by ΔG and ΣG, see Figure 7) that results in ND suppression in the voltage signal. This nonlinearity, which is a consequence of the biophysical model that captures T5 responses, enables greater selectivity than a single dof transformation (for intution, see Figure 7). Since our model does not explain the PD enhancement observed in calcium measurements (e.g. Fisher et al., 2015; Salazar-Gatzimas et al., 2016; Haag et al., 2016), we augment this model with a voltage-to-calcium transformation.
Tables
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Genetic reagent (D. melanogaster) | UAS-GFP | Janelia Research Campus | pJFRC28-10XUAS-IVS-GFP-p10 (attP2) | Rubin Lab JFRC28 |
| Genetic reagent (D. melanogaster) | Stable split Gal4 (T5) | Janelia Research Campus | w; VT055812-AD(attP40); R47H05-DBD(attP2) | Rubin Lab SS25175 |
| Software, algorithm | MATLAB | Mathworks Inc | 2018b |
Additional files
-
Supplementary file 1
Excitation-Inhibition model parameters (related to Figures 4, 5 and 7).
- https://cdn.elifesciences.org/articles/50706/elife-50706-supp1-v2.docx
-
Supplementary file 2
Excitation-Removal of excitation model parameters (related to Figures 6 and 7).
- https://cdn.elifesciences.org/articles/50706/elife-50706-supp2-v2.docx
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/50706/elife-50706-transrepform-v2.pdf
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The computation of directional selectivity in the Drosophila OFF motion pathway
eLife 8:e50706.
https://doi.org/10.7554/eLife.50706
