Reconfiguration of functional brain networks and metabolic cost converge during task performance
- Department of Psychiatry and Psychotherapy, Medical University of Vienna, Austria
- QIMR Berghofer Medical Research Institute, Australia
- School of Psychology, University of Newcastle, Australia
- Department of Biomedical Imaging and Image-guided Therapy, Division of Nuclear Medicine, Medical University of Vienna, Austria
- Center for Biomarker Research in Medicine (CBmed), Austria
Figures
Figure 1
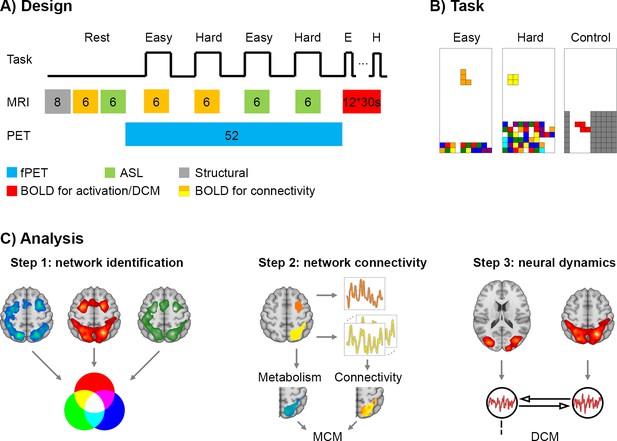
Design and work flow.
(A) The experimental sequence comprised a T1-weighted structural scan (8 min, grey), BOLD (6 min, orange) and ASL (6 min, green) at rest. This was followed by task-specific PET/MR acquisition. During the fPET measurement (52 min, blue) participants completed four times (6 min each) the video game Tetris with two levels of cognitive load. Simultaneous MRI acquisition included BOLD used to estimate functional connectivity (orange) and ASL (green). In the final part of the experiment, participants performed 12 task blocks (easy, hard and control, 30 s for each block, red) during BOLD acquisition to estimate neural task effects and to compute effective connectivity using dynamic causal modeling. Numbers indicate the duration of blocks in minutes unless indicated otherwise. (B) Task load (easy and hard) was defined by the speed of the falling bricks and the amount of bricks at the bottom. In the control condition the bricks were navigated through the channel, but no lines could be built as bricks vanished afterwards. (C) Data analysis comprised three main steps (same color codes as in A). First, brain regions involved in task processing were identified as conjunction of task-specific changes in glucose metabolism (fPET), blood oxygenation (BOLD) and blood flow (ASL). Second, the interplay between these brain regions was determined by the combination of metabolism and functional connectivity at rest and during task performance. Seed-to-voxel correlations were calculated to obtain patterns of functional connectivity. Metabolic connectivity mapping (MCM) (Riedl et al., 2016) was then computed by correlating the regional patterns of metabolic demands and functional connectivity with the inference of directionality if these spatial patterns show a significant association. Third, to assess the putative link between MCM and neural dynamics, the resulting MCM model was compared to the one obtained using dynamic causal modeling (DCM).
Figure 2 with 1 supplement
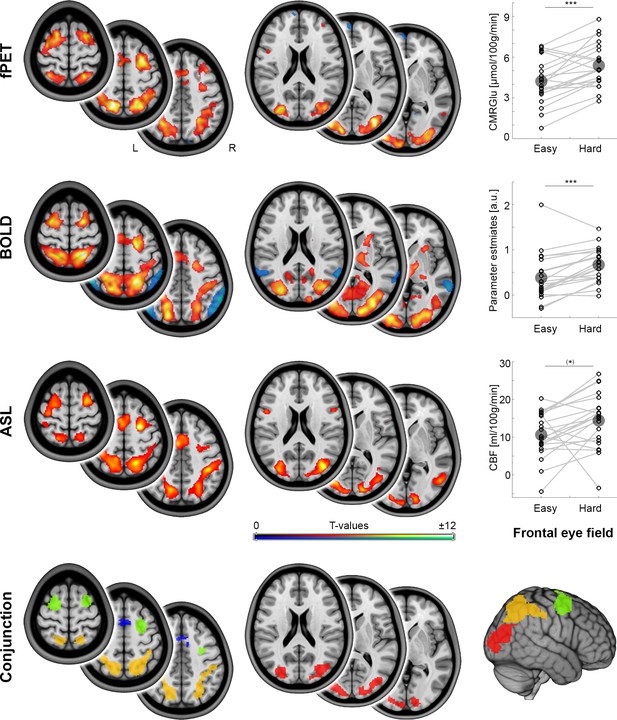
Local metabolism and neural activity.
Task-specific changes of different metabolic demands as obtained with functional PET (fPET), blood oxygen level dependent (BOLD) signal and arterial spin labeling (ASL, all pFWE < 0.05 corrected cluster level), respectively. fPET and ASL maps refer to the contrast hard > baseline, whereas BOLD maps reflect the contrast hard > control (these differ due to the manner in which the data were acquired). Dot plots depict within subject changes in glucose metabolism (CMRGlu), BOLD signal and cerebral blood flow (CBF) as a function of increasing task load in the frontal eye field (FEF, from the conjunction analysis; (*)p = 0.07, ***p < 0.001, corrected; large circles indicate group mean values). The conjunction map shows the spatial overlap (intersection) across the three imaging modalities in the occipital cortex (red), intraparietal sulcus (orange), frontal eye field (green) and supplementary motor area (blue). Since the supplementary motor area did not show significant changes as a function of cognitive demands for CMRGlu and CBF, this region was not included in the subsequent MCM and DCM analyses. Axial slices are shown in neurological convention (left is left) at z = 0, 10 and 20 mm as well as 45, 55 and 65 mm.
-
Figure 2—source data 1
Task-induced changes CMRGlu, CBF and BOLD signal.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig2-data1-v2.txt
Figure 2—figure supplement 1
Task-induced changes in glucose metabolism obtained with an fMRI-independent baseline definition.
To compute task-specific CMRGlu estimates independent of BOLD changes, fPET was also calculated using a method previously developed by our group (Hahn et al., 2016). In this method, the baseline term was modeled as a third-order polynomial while including task regressors as nuisance variables. This approach allows to estimate a task-free baseline term. Adopting this baseline definition showed similar results, whereas the original baseline provided a slightly more conservative estimate of CMRGlu changes. The spatial overlap between fPET and BOLD was also similar between the two approaches (Dice coefficient = 0.53 vs 0.49 with the original approach presented in Figure 2). Axial slices are shown in neurological convention (left is left) at z = 0, 10 and 20 mm as well as 45, 55 and 65 mm.
Figure 3 with 3 supplements
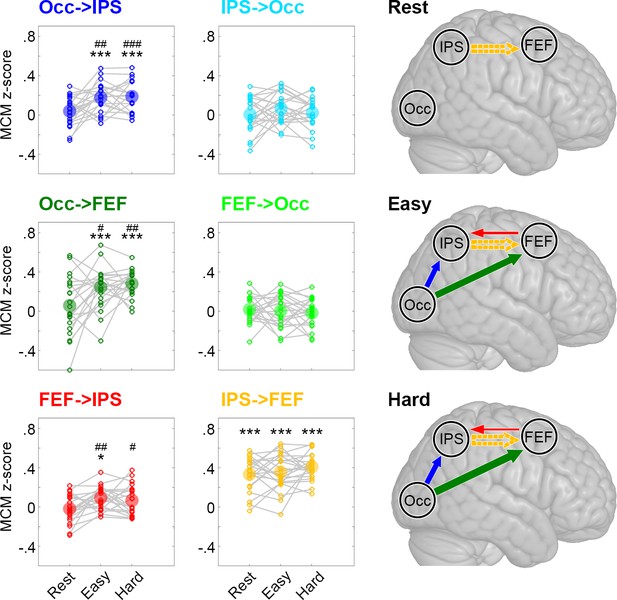
Metabolic connectivity mapping (MCM).
MCM was calculated as correlation between glucose metabolism and functional connectivity across all subjects (z-transformed Pearson’s r values). The small circles in the plots show z-scores of individual subjects and the big semitransparent circles indicate group mean values. At rest, only the link IPS -> FEF showed a significant correlation between metabolism and functional connectivity (orange). This correlation remained stable across all levels of task load (easy and hard). Crucially, we observed a marked increase in the correlations between metabolism and functional connectivity during task performance for Occ -> IPS (dark blue), Occ -> FEF (dark green) and FEF -> IPS (red). Changes in task load only altered the strength of these associations but not the overall pattern of interactions within the network. The resulting models for the three different conditions are schematically shown in the right panel, with the arrow thickness being proportional to the correlation strength. Solid and dashed arrows indicate connections with and without task modulation, respectively. FEF: frontal eye field, IPS: intraparietal sulcus, Occ: occipital cortex. Significant differences compared to zero *p < 0.05, **p < 0.01, ***p < 0.001 and compared to rest #p < 0.05, ##p < 0.01, ###p < 0.001, all corrected for multiple comparisons using the Bonferroni-Holm procedure.
-
Figure 3—source data 1
Metabolic connectivity mapping data.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig3-data1-v2.txt
Figure 3—figure supplement 1
Comparison between functional connectivity (FC) and metabolic connectivity mapping (MCM, as shown in Figure 3).
Similar to MCM, also functional connectivity was sensitive to task performance and showed significant increases from rest to task for all three connections. As functional connectivity by definition provides undirected information, only the additional assessment of the underlying glucose metabolism enables a specific assignment of the influence one region exerts on another. Significant differences compared to zero *p < 0.05, **p < 0.01, ***p < 0.001 and compared to rest #p < 0.05, ##p < 0.01, ###p < 0.001, all corrected for multiple comparisons using the Bonferroni-Holm procedure.
-
Figure 3—figure supplement 1—source data 1
Functional connectivity data.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig3-figsupp1-data1-v2.txt
Figure 3—figure supplement 2
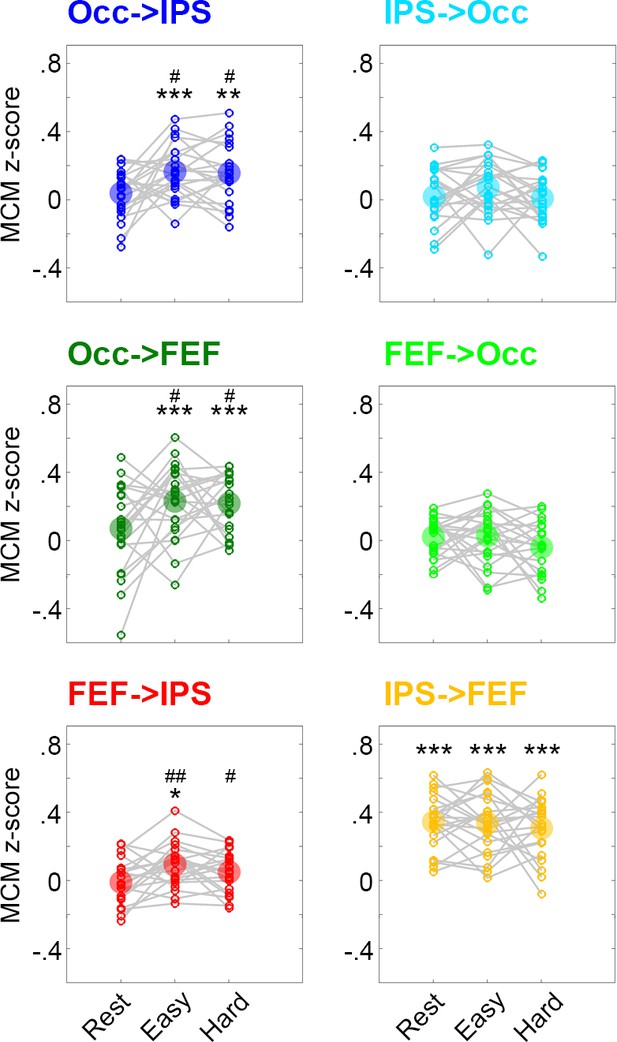
Impact of functional connectivity preprocessing on metabolic connectivity mapping (MCM).
It has been suggested that the order of common preprocessing steps may impact the estimates of functional connectivity, especially when performing motion scrubbing (Carp, 2013). To directly test this possibility, we re-calculated functional connectivity using an approach that performs the entire processing (regression, filtering, motion scrubbing) in a single step. This approach is therefore insensitive to the order of the different preprocessing steps (Hallquist et al., 2013). Computation of MCM values adopting the new estimates of functional connectivity yielded similar results compared to the original MCM estimates. Abbreviations and color codes are identical to Figure 3. Significant differences compared to zero *p < 0.05, **p < 0.01, ***p < 0.001 and compared to rest #p < 0.05, ##p < 0.01, ###p < 0.001, all corrected for multiple comparisons using the Bonferroni-Holm procedure.
-
Figure 3—figure supplement 2—source data 1
Metabolic connectivity mapping data with alternative functional connectivity preprocessing.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig3-figsupp2-data1-v2.txt
Figure 3—figure supplement 3
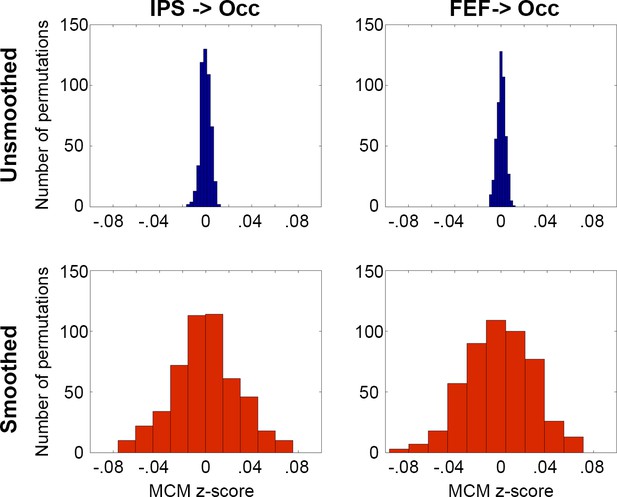
Influence of spatial smoothing on MCM estimates.
Unsmoothed data on functional connectivity and CMRGlu were separately permuted across voxels, yielding MCM values tightly centered on zero (blue bars, z = 0.00005 ± 0.004). Spatial smoothing still showed MCM estimates close to zero, but with a slightly higher variance (red bars, z = −0.001 ± 0.03).
-
Figure 3—figure supplement 3—source data 1
Unsmoothed random permutation MCM data for IPS -> Occ.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig3-figsupp3-data1-v2.txt
-
Figure 3—figure supplement 3—source data 2
Smoothed random permutation data for IPS -> Occ.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig3-figsupp3-data2-v2.txt
-
Figure 3—figure supplement 3—source data 3
Unsmoothed random permutation MCM data for FEF -> Occ.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig3-figsupp3-data3-v2.txt
-
Figure 3—figure supplement 3—source data 4
Smoothed random permutation MCM data for FEF -> Occ.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig3-figsupp3-data4-v2.txt
Figure 4 with 3 supplements
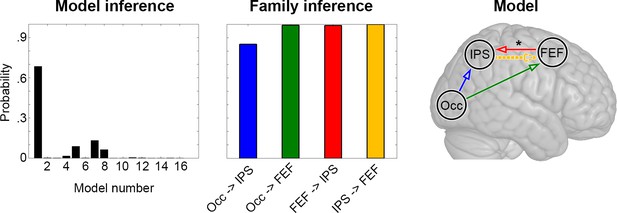
Dynamic causal modeling (DCM).
Inference across the entire model space indicates the highest probability for the first model, which corresponds to the model resulting from the MCM analysis (Figure 3). Testing each task modulation and effective connection with family inference confirms the relevance of the individual links, with posterior probabilities close to one for all connections with the exception of Occ -> IPS. A modulation of effective connectivity as a function of task load was observed for the connection FEF -> IPS (*p < 0.05). See Figure 3 for abbreviations and color code of connections as well as Figure 4—figure supplement 2 for model space.
-
Figure 4—source data 1
Probability of DCM models.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig4-data1-v2.txt
-
Figure 4—source data 2
Probability of DCM family inference.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig4-data2-v2.txt
Figure 4—figure supplement 1
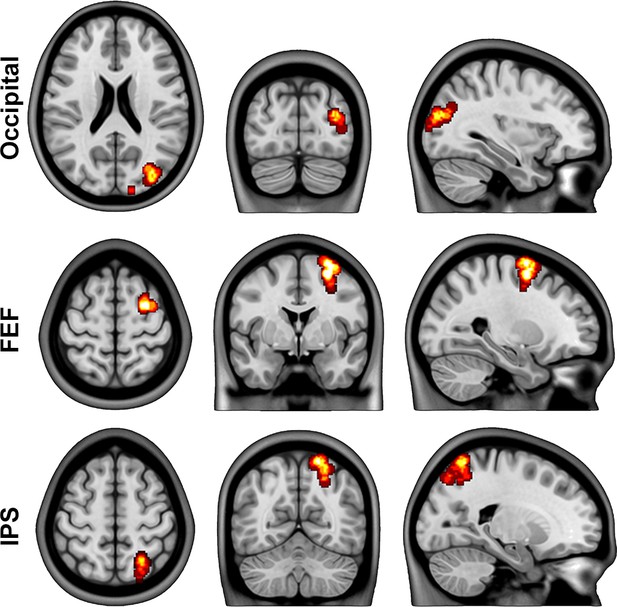
Dynamic causal modeling (DCM) regions.
BOLD time series were extracted from spheres of 5 mm radius, each individually shifted to the location with the maximum effect size in the analysis of task changes (F-test) and constrained by the conjunction map depicted in Figure 2. For visualization purposes, the individual spheres were binarized and summed across all subjects. The resulting maps show the locations in the occipital cortex (Occ, x/y/z = 33/−81/21 mm), frontal eye field (FEF, x/y/z = 27/0/61 mm) and intraparietal sulcus (IPS x/y/z = 21/−61/56 mm).
Figure 4—figure supplement 2
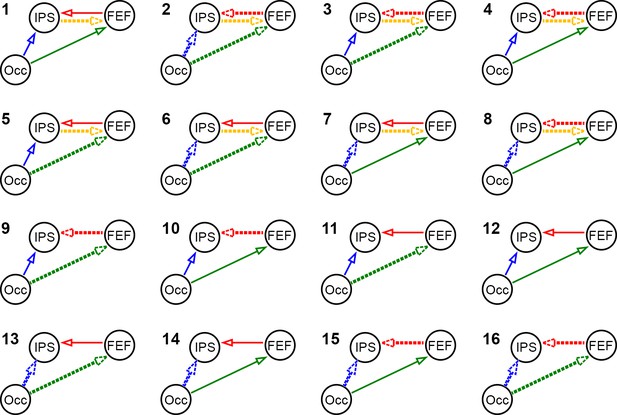
Dynamic causal modeling (DCM) space.
For the effective connections Occ –> IPS, Occ -> FEF and FEF –> IPS the relevance of task modulation was tested, whereas for the connection IPS -> FEF the relevance of the intrinsic connection was tested, as based on the MCM results (Figure 3). This yields 24 = 16 models that were evaluated using Bayesian model selection. For family inference, models with a certain connection were tested against those without it. Family Occ -> IPS included models 1, 3, 4, 5, 9, 10, 11, 12; family Occ -> FEF included models 1, 4, 7, 8, 10, 12, 14, 15; family FEF -> IPS included models 1, 5, 6, 7, 11, 12, 13, 14 and family IPS -> FEF included models 1–8. The occipital cortex was the driving input for all models. Solid and dashed arrows indicate connections with and without task modulation, respectively. FEF: frontal eye field, IPS: intraparietal sulcus, Occ: occipital cortex.
Figure 4—figure supplement 3
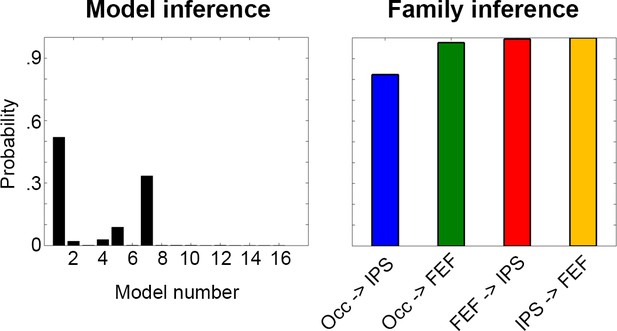
DCM results with a region of interest size of 8 mm.
Similar to the results from the original analysis (Figure 4), model one showed the highest posterior probability and family inference indicated high probabilities for all four connections.
-
Figure 4—figure supplement 3—source data 1
Probability of DCM models with 8 mm smoothing.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig4-figsupp3-data1-v2.txt
-
Figure 4—figure supplement 3—source data 2
Probability of DCM family inference with 8 mm smoothing.
- https://cdn.elifesciences.org/articles/52443/elife-52443-fig4-figsupp3-data2-v2.txt
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Reconfiguration of functional brain networks and metabolic cost converge during task performance
eLife 9:e52443.
https://doi.org/10.7554/eLife.52443
