Meta-Research: Dataset decay and the problem of sequential analyses on open datasets
Figures
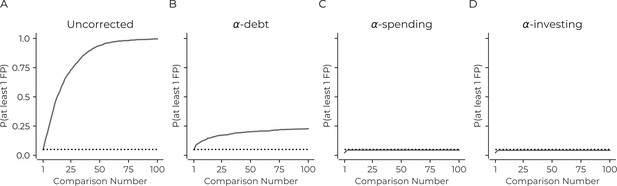
Correction procedures can reduce the probability of false positives.
(A) The probability of there being at least one false positive (y-axis) increases as the number of statistical tests increases (x-axis). The use of a correction procedure reduces the probability of there being at least one false positive (B: α-debt; C: α-spending; D: α-investing). Plots are based on simulations: see main text for details. Dotted line in each panel indicates a probability of 0.05.
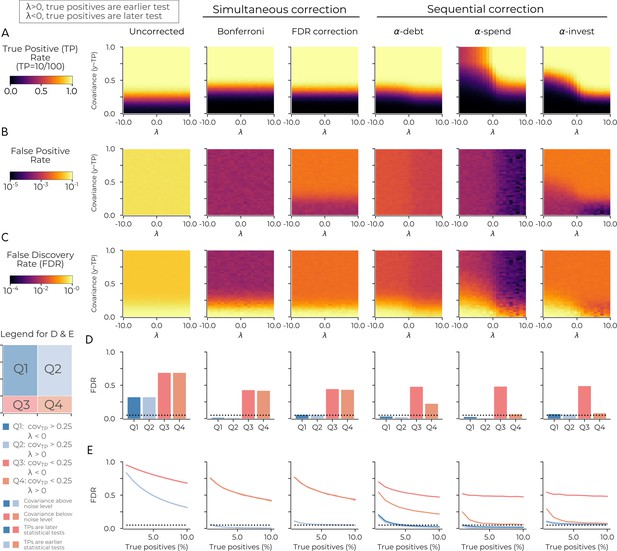
The order of sequential tests can impact true positive sensitivity.
(A) The true positive rate in the uncorrected case (left-most panel), in two cases of simultaneous correction (second and third panels), and in three cases of sequential correction (fourth, fifth and sixth panels). In each panel the true positive rate after 100 tests is plotted as a function of two simulation parameters: λ (x-axis) and the simulated covariance of the true positives (y-axis). When λ is positive (negative), it increases the probability of the true positives being an earlier (later) test. Plots are based on simulations in which there are ten true positives in the data: see main text for details. (B) Same as A for the false positive rate. (C) Same as A for the false discovery rate. (D) Same as C for the average false discovery rate in four quadrants. Q1 has λ <0; covariance >0.25. Q2 has λ >0; covariance >0.25. Q3 has λ <0; covariance <0.25. Q4 has λ >0; covariance <0.25. The probability of true positives being an earlier test is highest in Q2 and Q4 as λ >0 in these quadrants. (E) Same as D with the false discovery rate (y-axis) plotted against the percentage of true positives (x-axis) for the four quadrants. The dotted lines in D and E indicate a false discovery rate of 0.05. Code is available at https://github.com/wiheto/datasetdecay (Thompson, 2020; copy archived at https://github.com/elifesciences-publications/datasetdecay).
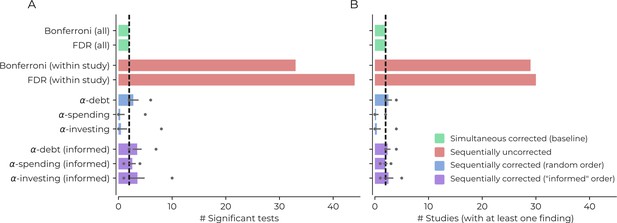
Demonstrating the impact of different correction procedures with a real dataset.
(A) The number of significant statistical tests (x-axis) that are possible for various correction procedures in a real dataset from the Human Connectome Project: see the main text for more details, supplementary file 1 for a list of the variables used in the analysis, and https://github.com/wiheto/datasetdecay copy archived at https://github.com/elifesciences-publications/datasetdecay for the code. (B) The potential number of publications (x-axis) that could result from the tests shown in panel A. This assumes that a publication requires a null hypothesis to be rejected in order to yield a positive finding. The dotted line shows the baseline from the two simultaneous correction procedures. Error bars show the standard deviation and circles mark min/max number of findings/studies for the sequential correction procedures with a randomly permuted test order.
Tables
Summary of the different sequential correction methods and the open-data desiderata.
Yes indicates that the method is compatible with the desideratum.
| Sharing incentive | Open access | Stable false positive rate | |
|---|---|---|---|
| -spending | No | No | Yes |
| -investing | Yes | No | Yes |
| -debt | Yes | Yes | No |
Additional files
-
Supplementary file 1
The variables selected for analysis in Figure 3.
- https://cdn.elifesciences.org/articles/53498/elife-53498-supp1-v1.csv
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/53498/elife-53498-transrepform-v1.docx





