A circuit mechanism for decision-making biases and NMDA receptor hypofunction
- Department of Clinical and Movement Neurosciences, University College London, United Kingdom
- Department of Physics, Yale University, United States
- Department of Psychiatry, Yale University School of Medicine, United States
- Wellcome Trust Centre for Neuroimaging, University College London, United Kingdom
- Max Planck-UCL Centre for Computational Psychiatry and Aging, University College London, United Kingdom
- Wellcome Centre for Integrative Neuroimaging, Department of Psychiatry, University of Oxford, United Kingdom
Figures
Figure 1
An evidence-varying decision-making task for macaque monkeys.
(A) Task design. Two streams of stimuli were presented to a monkey, both of which consisted of a sequence of eight samples of bars of varying heights. Depending on the contextual cue shown at the start of the trial, the monkey had to report the stream with either taller or shorter mean bar height. On correct trials, the monkey was rewarded proportionally to the mean evidence for the correct stream; incorrect trials were not rewarded. The monkey was required to fixate centrally while the evidence was presented, indicated by the dashed red fixation zone (not visible to subject). (B) Generating process of each stimulus stream. The generating mean for each trial was chosen from a uniform distribution (see Materials and methods), while the generating standard deviation was 12 and 24 for the narrow (brown) and broad (blue) streams respectively. (C) Example Trial. The bar heights in both streams varied over time. The dotted lines illustrate the mean of the eight stimuli for the narrow/broad streams. In this example, the narrow stream has taller mean bar height and thus more mean evidence strength, so is the correct choice. The narrow/broad streams are randomly assigned to the left/right options on different trials; in the example trial shown here (A and C), the narrow stream is assigned to the right option, the broad stream is assigned to the left option.
Figure 2 with 1 supplement
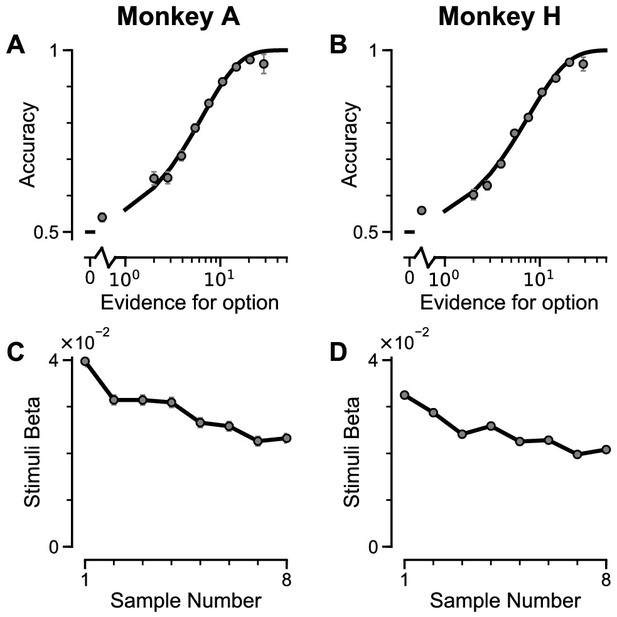
Subjects use evidence presented throughout the trial to guide their choices.
(A-B) Choice accuracy plotted as a function of the amount of evidence in favour of the best option. Lines are a psychometric fit to the data. (C-D) Logistic regression coefficients reveal the contribution (weight) of all eight stimuli on subjects’ choices (see Materials and methods). Although subjects used all eight stimuli to guide their choices, they weighed the initially presented evidence more strongly. All errorbars indicate the standard error.
Figure 2—figure supplement 1
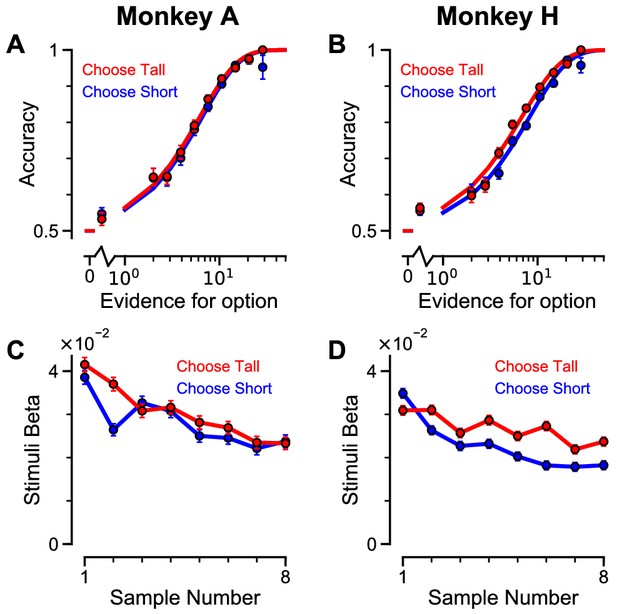
Subjects use evidence presented throughout the trial to guide their choices – data separated by ‘ChooseTall’ and ‘ChooseShort’ trials.
The psychometric functions and evidence weightings are very similar on ‘ChooseTall’ (red) and ‘ChooseShort’ (blue) trials. (A–B) Choice accuracy plotted as a function of the amount of evidence in favour of the best option. Lines are a psychometric fit to the data. (C–D) Logistic regression coefficients reveal the contribution (weight) of all eight stimuli on subjects’ choices (see Materials and methods). Although subjects used all eight stimuli to guide their choices, they weighed the initially presented evidence more strongly. All errorbars indicate the standard error.
Figure 3 with 2 supplements
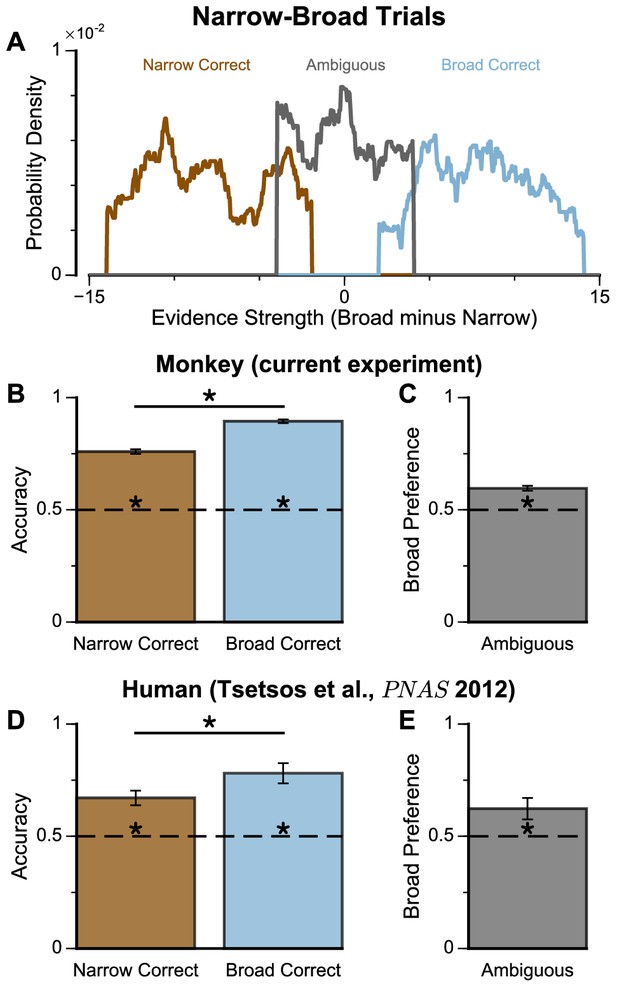
Subjects show a pro-variance bias in their choices on Narrow-Broad Trials, mirroring previous findings in human subjects.
(A) The narrow-broad trials include three types of conditions, where either the narrow stream is correct (brown), the broad stream is correct (blue), or the difference in mean evidence is small (grey, ‘Ambiguous’ trials). See Materials and methods and Figure 3—figure supplement 1 for details of the generating process. (B–C) Monkey choice performance on Narrow-Broad trials. (B) Subjects were significantly more accurate on ‘Broad-correct’ trials (Chi-squared test, chi = 99.05, p<1×10−10). Errorbars indicate the standard error. (C) Preference for the broad option on ‘Ambiguous’ trials. Subjects were significantly more likely to choose the broad option (Binomial test, p<1×10−10). Errorbar indicates the standard error. (D–E) Human choice performance on Narrow-Broad trials previously reported by Tsetsos et al., 2012. (D) Choice accuracy when either the narrow or the broad stream is correct, respectively. Subjects were more accurate on ‘Broad-correct’ trials. (E) Preference for the broad option on ‘Ambiguous’ trials. Subjects were more likely to choose the broad option.
Figure 3—figure supplement 1
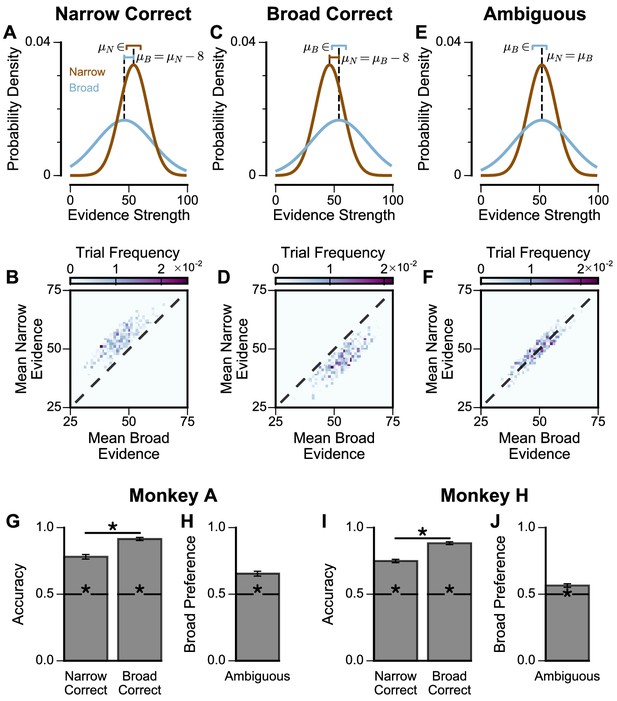
Extra Information on Narrow-Broad Trials, separated by subjects.
(A) The generating process of the narrow-correct trials, for each narrow (brown) and broad (blue) stimuli sample. A full stream sequentially presents 8 such stimuli, each for 200ms with a 50ms inter-sample interval in between. In each trial where the narrow choice is correct, the generating mean of the narrow stream, , is uniformly sampled from [48,60]. The generating mean of the broad stream, , is then set to be . For all trials, the generating standard deviation of the narrow and broad streams are , respectively. The lines above the distributions denote the ranges of and . The particular values of and in this figure are shown for one trial, and chosen arbitrarily for illustration purpose. Given the generating means and standard deviations in a trial, a sequence of 8 stimuli samples are generated from a Gaussian process with certain constraints, for each of the narrow and broad options (See Materials and methods). (B) Sampled distribution of the mean evidence of the narrow and broad streams, across all trials for both monkeys where the narrow option is correct. (C, D) Same as (A, B) but for broad-correct trials. Here, is uniformly sampled from [48,60], and is set to be . (E, F) Same as (A, B) but for ambiguous trials. Here, and are equal and uniformly sampled from [44,56]. (G) The accuracy of Monkey A in the narrow-correct and broad-correct trials. Monkey A was significantly more accurate on ‘Broad-correct’ trials (Chi-squared test, chi = 38.39, p = 5.80x10−10). Errorbars show the standard error. (H) The probability for Monkey A to choose the broad option in ambiguous trials. Monkey A was significantly more likely to choose the broad option (Binomial test, p < 1x10−10). (I) Same as (G) but for Monkey H (Chi-squared test, chi = 59.46, p < 1x10−10). (J) Same as (H) but for Monkey H (Binomial test, p = 3.00x10−6).
Figure 3—figure supplement 2
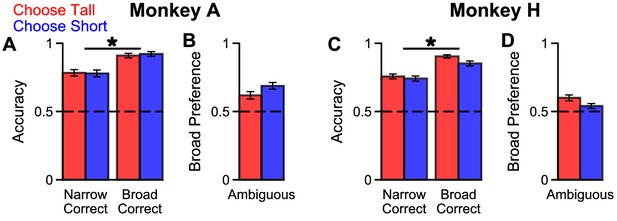
Extra Information on Narrow-Broad Trials, separated by ‘ChooseTall’ and ‘ChooseShort’ trials.
The findings are very similar on ‘ChooseTall’ (red) and ‘ChooseShort’ (blue) trials. (A) The accuracy of Monkey A in the narrow-correct and broad-correct trials. Monkey A was significantly more accurate on ‘Broad-correct’ trials (Chi-squared test, chi(ChooseTall) = 18.66, p(ChooseTall) = 1.57×10−5, chi(ChooseShort) = 19.87, p (ChooseShort) = 8.30×10−6). Errorbars show the standard error. (B) The probability for Monkey A to choose the broad option in ambiguous trials. Monkey A was significantly more likely to choose the broad option (Binomial test, p(ChooseTall)=2.29×10−5, p (ChooseShort) = p < 10−10). (C) Same as (A) but for Monkey H (Chi-squared test, chi(ChooseTall) = 43.52, p(ChooseTall)=p < 10−10, chi(ChooseShort) = 16.19, p (ChooseShort) = 5.74×10−5). (D) Same as (B) but for Monkey H (Binomial test, p(ChooseTall)=3.47×10−6, p (ChooseShort) = 0.0314).
Figure 4 with 3 supplements
Subjects show a pro-variance bias in their choices on regular trials.
For these analyses, stimulus streams were divided into ‘Lower SD’ or ‘Higher SD’ options post-hoc, on a trial-wise basis. (A) On regular trials, the mean evidence of each stream was independent. (B) Each stream is sampled from either a narrow or a broad distribution, such that about 50% of the trials have one broad stream and one narrow stream, 25% of the trials have two broad streams, and 25% of the trials have two narrow streams. (C) Psychometric function when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct in the regular trials. (D) Regression analysis using the left-right differences of the mean and standard deviation of the stimuli evidence to predict left choice. The beta coefficients quantify the contribution of both statistics to the decision-making processes of the monkeys (Mean Evidence: t = 74.78, p<10−10; Evidence Standard Deviation: t = 19.65, p<10−10). Notably, a significantly positive evidence SD coefficient indicates the subjects preferred to choose options which were more variable across samples. Errorbars indicate the standard error.
Figure 4—figure supplement 1
Extra information on Regular Trials, separated by subjects.
In the regular-trials, each of the two streams is randomly chosen to be either narrow (), or broad (), then divided into ‘Lower SD’ or ‘Higher SD’ options post-hoc, depending on the sampled standard deviation of evidence relative to the other option. (A) The distribution of the mean evidence of ‘Lower SD’ and ‘Higher SD’ streams, across all regular trials for both monkeys. (B) The distribution of the evidence variability of ‘Lower SD’ and ‘Higher SD’ streams, across all regular trials for both monkeys. (C) The psychometric function of Monkey A when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct. (D) A regression model using evidence mean and variability to predict the animals’ choices. Each regressor is the left-right difference of the mean and standard deviation of the evidence streams. This shows that both statistics are utilised by Monkey A to solve the task (Mean Evidence: t = 45.90, p < 10−10; Evidence Standard Deviation: t = 16.68, p < 10−10). (E) A regression model including the mean, maximum, minimum, first, and last evidence values of both the left and right streams as regressors, in order to evaluate the contribution of each quantity and the possibility that the monkey is utilising strategies alternative to evidence integration and pro-variance bias. Evidently, Monkey A mainly relies on temporal integration to solve the task, as indicated by a strong mean evidence coefficient in both regression models. See also Supplementary files 1, 2, 3 for cross-validation analysis comparing regression models including various combinations of these predictors. (F–H) Same as (C–E) but for Monkey H. The statistics of the regression model in (G) are (Mean Evidence: t = 58.88, p < 10−10; Evidence Standard Deviation: t = 12.08, p < 10−10). All errorbars indicate the standard error.
Figure 4—figure supplement 2
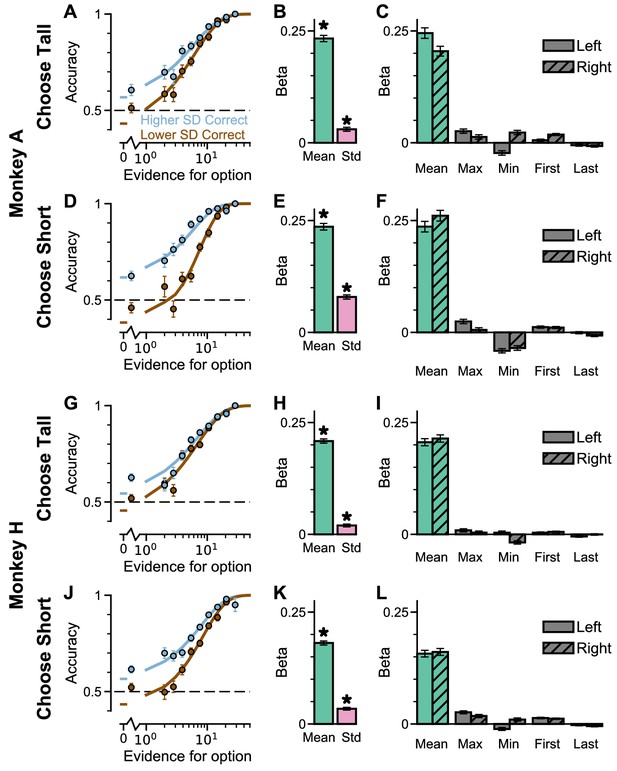
Extra information on Regular Trials, separated by ‘ChooseTall’ and ‘ChooseShort’ trials.
The findings are very similar on both trial types. (A) The psychometric function of Monkey A when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct, on ‘ChooseTall’ trials. (B) A regression model using evidence mean and variability to predict Monkey A’s choices on ‘ChooseTall’ trials. Each regressor is the left-right difference of the mean and standard deviation of the evidence streams. This shows that both statistics are utilised by Monkey A to solve the task (mean evidence: t(ChooseTall) = 32.78, p(ChooseTall)<10−10; evidence standard deviation: t(ChooseTall) = 6.81, p(ChooseTall)<10−10). (C) A regression model including the mean, maximum, minimum, first, and last evidence values of both the left and right streams as regressors, in order to evaluate the contribution of each quantity on choices on ‘ChooseTall’ trials and the possibility that Monkey A is utilising strategies alternative to evidence integration and pro-variance bias. Evidently, Monkey A mainly relies on temporal integration to solve the task, as indicated by a strong mean evidence coefficient in both regression models. (D) The psychometric function of Monkey A when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct, on ‘ChooseShort’ trials. (E) The same regression model as (B) applied to Monkey A’s choices on ‘ChooseShort’ trials (mean evidence: t(ChooseShort) = 32.09, p(ChooseShort)<10−10; evidence standard deviation: t(ChooseShort) = 16.47, p(ChooseShort)<10−10). (F) The same regression model as (C) applied to Monkey A’s choices on ‘ChooseShort’ trials. (G–L) Same as (A–F) but for Monkey H. The statistics of the regression model in (H) are (mean evidence: t(ChooseTall) = 42.76, p(ChooseTall)<10−10; evidence standard deviation: t(ChooseTall) = 6.19, p(ChooseTall)=5.92−10), and (K) are (mean evidence: t(ChooseShort) = 40.43, p(ChooseShort)<10−10; evidence standard deviation: t(ChooseShort) = 10.97, p(ChooseShort)<10−10). All errorbars indicate the standard error.
Figure 4—figure supplement 3
Extra information on Regular Trials – the subjects do not show a frequent winner bias.
(A) A regression model using evidence mean and the number of local winners to predict Monkey A’s choices. This shows that after controlling for mean evidence, Monkey A did not have a frequent winner bias (Mean Evidence: t = 34.86, p<10−10; Local Wins: t = 1.26, p=0.2068). (B) Same as (A) but for Monkey H. The statistics of the regression model in (B) are (Mean Evidence: t = 44.33, p<10−10; Local Wins: t = 0.048, p=0.9614). All errorbars indicate the standard error.
Figure 5 with 2 supplements
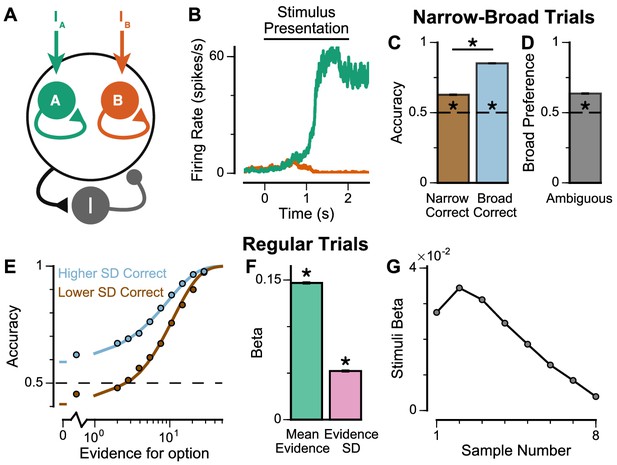
Spiking cortical circuit model reproduces pro-variance bias.
(A) Circuit model schematic. The model consists of two excitatory neural populations which receive separate inputs (IA and IB), each reflecting the momentary evidence for one of the two stimuli streams. Each population integrates evidence due to recurrent excitation, and competes with the other via lateral inhibition mediated by a population of interneurons. (B) Example firing rate trajectories of the two populations on a single trial where option A is chosen. (C, D) Narrow-Broad Trials. (C) The circuit model is significantly more accurate when the broad stream is correct, than when the narrow stream is correct (Chi-squared test, chi = 1981, p<1×10−10). (D) On ‘Ambiguous trials’, the circuit model is significantly more likely to choose the broad option (Binomial test, p<1×10−10). (E–G) Regular trials. (E) The psychometric function of the circuit model when either the ‘Lower SD’ (brown) or ‘Higher SD’ (blue) stream is correct, respectively. (F) Regression analysis of the circuit model choices on regular trials, using evidence mean and variability as predictors of choice. Both quantities contribute to the decision-making process of the circuit model (Mean Evidence: t = 129.50, p<10−10; Evidence Standard Deviation: t = 45.27, p<10−10). (G) Regression coefficients of the stimuli at different time-steps, showing the time course of evidence integration. The circuit demonstrates a temporal profile which decays over time, similar to the monkeys. All errorbars indicate the standard error.
Figure 5—figure supplement 1
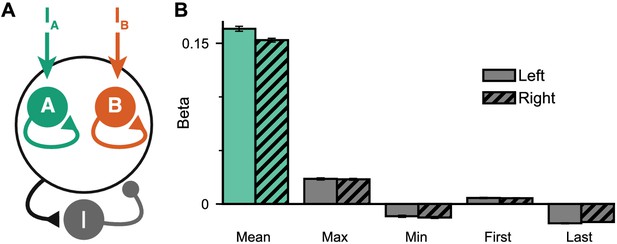
Extended regression results on the circuit model performance.
(A) Circuit model schematic. The model consists of two excitatory populations which receive separate inputs, reflecting evidence for the two stimuli streams. Each population integrates evidence due to recurrent excitation, and competes with the other due to lateral inhibition. (B) Regression analysis of the regular trial circuit model data, using the mean, maximum, minimum, first, and last evidence values of both the left and right streams, in order to evaluate the possibility of decision-making strategies alternative to evidence integration and pro-variance bias. Similar to the monkeys, the circuit model mainly relies on mean evidence to solve the task. See also Supplementary files 1–3 for cross-validation analysis comparing regression models including various combinations of these predictors. All errorbars indicate the standard error.
Figure 5—figure supplement 2
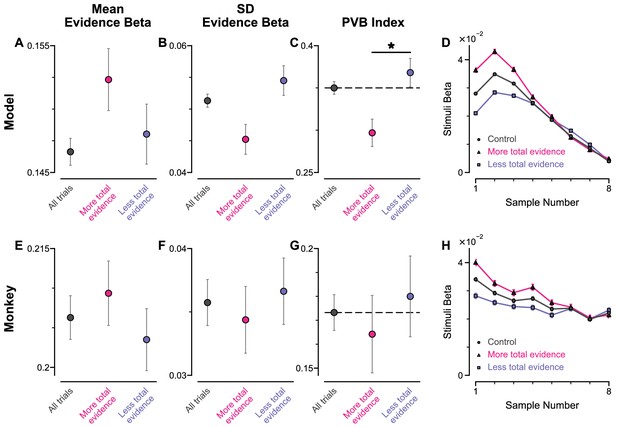
Pro-variance bias and temporal weightings in trials separated with more or less total evidence, for circuit model and monkey data.
(A–C) Regression analysis of the circuit model choices, using evidence mean and variability as predictors, on all regular trials (grey), half of the regular trials with more total evidence (pink), and half of the regular trials with less total evidence (blue). (A) Regression coefficient for mean evidence. The regression coefficient for mean evidence is not significantly different between trials with more total evidence and trials with less total evidence (permutation test, p=0.8366). (B) Regression coefficient for evidence standard deviation. The regression coefficient for evidence standard deviation is not significantly different between trials with more total evidence and trials with less total evidence (permutation test, p=0.8710). (C) PVB index. The PVB index is significantly higher for trials with less total evidence than for trials with more total evidence (permutation test, p=7×10−5) (D) Temporal regression weights using the three sets of trials. (E–H) Same as (A–D) but using the monkey behavioural data. The regression coefficients for mean evidence and evidence standard deviation are not significantly different between trials with more total evidence and trials with less total evidence (permutation tests, p(mean evidence)=0.9452, p(evidence standard deviation)=0.9869). The PVB index tends to be higher for trials with less total evidence than for trials with more total evidence, but the effect is insignificant (permutation test, p=0.3677). All errorbars indicate the standard error.
Figure 6 with 1 supplement
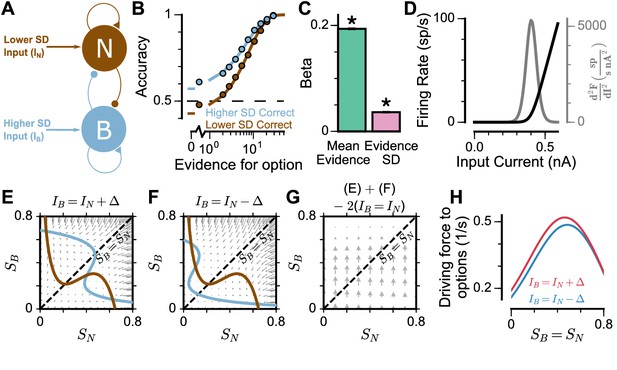
Mean-Field model explanation for pro-variance bias.
(A) The mean-field model of the circuit, with two variables representing evidence for the two options. For simplicity, we assume one stream is narrow and one is broad, and label the populations receiving the inputs as N and B respectively. (B) Psychometric function of regular trials as in (Figure 5E). (C) Regression analysis of the regular trial data as in (Figure 5F) (mean: t = 143.42, p < 10−10; standard deviation: t = 30.76, p < 10−10). Errorbars indicate the standard error. (D) The mean-field model uses a generic firing rate profile (black), with zero firing rate at small inputs, then a near-linear response as input increases (see Materials and methods). Such profiles have an expansive non-linearity (with a positive second order derivative (grey)) that can generate pro-variance bias. (E–H) An explanation of the pro-variance bias using phase-plane analysis. (E) A momentarily strong stimulus from the broad stream will drive the model to choose broad (large , small ). Blue and brown lines correspond to nullclines. (F) A momentarily weak stimulus in the broad stream will drive the model to choose narrow (large , small ). (G) The net effect of one strong and one weak broad stimulus, compared with two average stimuli, is to drive the system to the broad choice. That is, a momentarily strong stimulus has an asymmetrically greater influence on the decision-making process than a momentarily weak stimulus, leading to pro-variance bias. (H) The net drive to the broad or narrow option when the broad stimulus is momentarily strong (red) or weak (blue), along the diagonal ( in G).
Figure 6—figure supplement 1
Extended regression results on the mean-field model performance.
(A) The mean-field model consists of two variables which represent the accumulated evidence for the two choice options. The two variables demonstrate self-excitation and mutual inhibition. (B) Regression model on the regular trial model data, using the mean, maximum, minimum, first, and last evidence values of both the left and right streams, in order to evaluate the possibility of decision-making strategies alternative to evidence integration and pro-variance bias. Similar to the monkeys, the model mainly relies on mean evidence to solve the task. All errorbars indicate the standard error.
Figure 7 with 4 supplements
Predictions for E/I perturbations of the Spiking Circuit Model.
(A) Model perturbation schematic. Three potential perturbations are considered: lowered E/I (via NMDA-R hypofunction on excitatory pyramidal neurons), elevated E/I (via NMDA-R hypofunction on inhibitory interneurons), or sensory deficit (as weakened scaling of external inputs to stimuli evidence).(B–E) The regular-trial choice accuracy for each of the circuit perturbations (dark colour for when the ‘Higher SD’ stream is correct, light colour for when the ‘Lower SD’ stream is correct).(F–H) Regression analysis on the regular trial choices of the four models, using evidence mean and evidence variability to predict choice.(F) The mean evidence regression coefficients in the four models. Lowering E/I, elevating E/I, and inducing sensory deficits similarly reduce the coefficient, reflecting a drop in choice accuracy. (G) The evidence standard deviation regression coefficients in the four models. All three perturbations reduce the coefficient, but to a different extent. (H) The PVB index (ratio of evidence standard deviation coefficient over mean evidence coefficient) provides dissociable predictions for the perturbations. The lowered E/I circuit increases the PVB index relative to the control model (permutation test, p=6×10−5), while the elevated E/I circuit decreases the PVB index (permutation test, p<10−5). The PVB index is roughly maintained in the sensory deficit circuit (permutation test, p=0.6933). The dashed line indicates the PVB index for the control circuit, * indicates significant difference when the PVB index is compared with the control circuit. (I) The regression weights of stimuli at different time-steps for the four models. All errorbars indicate the standard error.
Figure 7—figure supplement 1
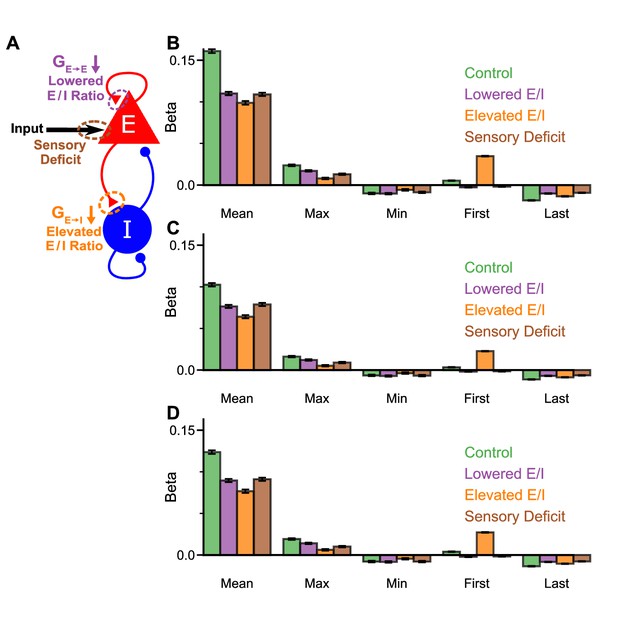
Model perturbations do not influence decision-making strategy.
(A) Model perturbation schematic. Three potential perturbations are considered: lowered E/I (via NMDA-R hypofunction on excitatory pyramidal neurons), elevated E/I (via NMDA-R hypofunction on inhibitory interneurons), or sensory deficit (as weakened scaling of external inputs to stimuli evidence). (B) The regression model using mean, maximum, minimum, first, and last evidence values of each of the left and right streams as regressors, for the four models. Each bar shows the average of the left and right regressors of the corresponding variable. None of the perturbed models demonstrate a significant shift in decision-making strategies. The elevated E/I circuit has a larger first evidence regression coefficient, due to over-emphasis of early stimuli (Figure 7I). All errorbars indicate the standard error. (C) Same as (B) but a proportion of the circuit models’ choices have been randomised according to the empirical lapse rate of Monkey A when administered with ketamine, then the regression weights re-calculated (see also Figure 8—figure supplement 8; Equation 6). (D) Same as (B) but with lapsing adjusted for that observed in Monkey H ketamine data (see also Figure 8—figure supplement 9).
Figure 7—figure supplement 2
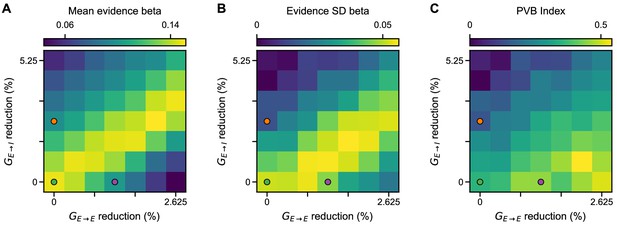
Regression analysis using evidence mean and evidence variability to predict choice, under simultaneous NMDA-R hypofunctions on excitatory and inhibitory neurons.
(A) The mean evidence regression coefficient for various models of NMDA-R hypofunctions on excitatory () and inhibitory () neurons. (B) The evidence standard deviation regression coefficient for various models of NMDA-R hypofunctions. (C) PVB index for various models of NMDA-R hypofunctions. PVB index robustly varies with E/I perturbation. In each plot, the green, purple, and orange dots respectively denote the control, lowered E/I, and elevated E/I circuit models used in Figure 7.
Figure 7—figure supplement 3
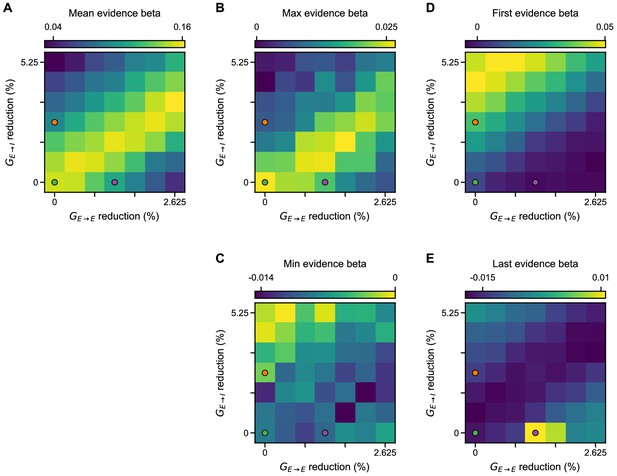
Regression analysis using mean, maximum, minimum, first, and last evidence values of each of the left and right streams as regressors, under simultaneous NMDA-R hypofunctions on excitatory and inhibitory neurons.
Each subplot shows the average of the left and right regressors of the corresponding variable. (A) Mean evidence regression coefficient for various models of NMDA-R hypofunctions on excitatory () and inhibitory () neurons. (B) Maximum evidence regression coefficient for various models of NMDA-R hypofunctions. (C) Minimum evidence regression coefficient for various models of NMDA-R hypofunctions. (D) First evidence regression coefficient for various models of NMDA-R hypofunctions. (E) Last evidence regression coefficient for various models of NMDA-R hypofunctions. In each plot, the green, purple, and orange dots respectively denote the control, lowered E/I, and elevated E/I circuit models used in Figure 7.
Figure 7—figure supplement 4
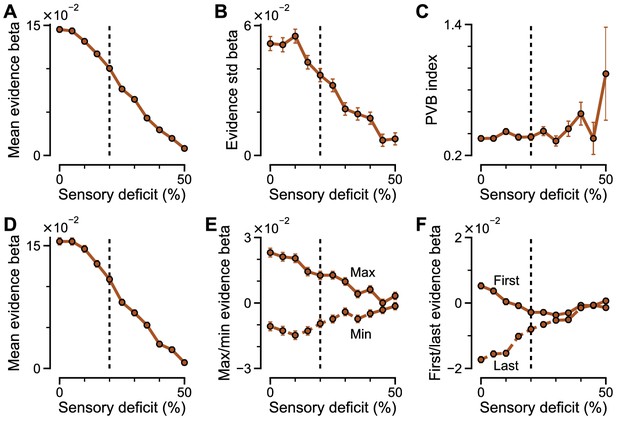
Regression coefficients and PVB index as a function of sensory deficit.
(A–C) Regression model with mean evidence and evidence standard deviation, and the resulting PVB index. The PVB index increases at very large sensory deficits, in a regime with minimal decision making performance that does not match to monkey behaviour under ketamine (see Figure 8—figure supplement 7). (D–F) Regression model with mean, max, min, first, last evidence. In each plot, the black vertical dash line denotes the sensory deficit perturbation strength used in Figure 7. All errorbars indicate the standard error.
Figure 8 with 9 supplements
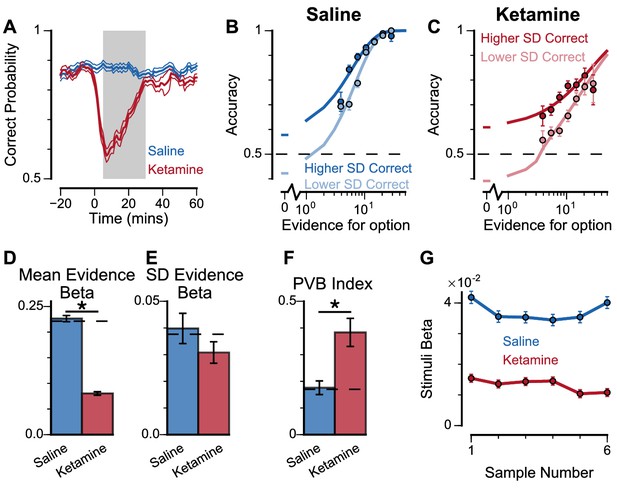
Experimental effects of ketamine on evidence accumulation behaviour produce an increased pro-variance bias, consistent with lowered excitation-inhibition balance.
(A) Mean percentage of correct choices across sessions made by monkeys relative to the injection of ketamine (red) or saline (blue). Shaded region denotes ‘on-drug’ trials (trials 5–30 min after injection) which are used for analysis in the rest of the figure. (B, C) The psychometric function when either the ‘Lower SD’ or ‘Higher SD’ streams are correct, with saline (B) or ketamine (C) injection. (D–F) Ketamine injection impairs the decision-making of the monkeys, in a manner consistent with the prediction of the lowered E/I circuit model. Dashed lines indicate pre-injection values in each plot. (D) The regression coefficient for mean evidence, under injection of saline or ketamine. Ketamine significantly reduces the coefficient (permutation test, p<1×10−6), reflecting a drop in choice accuracy. (E) The evidence standard deviation regression coefficient, under injection of saline or ketamine. Ketamine does not significantly reduce the coefficient (permutation test, p=0.152). (F) Ketamine increases the PVB index (permutation test, p=8×10−6), consistent with the model prediction of the lowered E/I circuit. (G) The regression weights of stimuli at different time-steps, for the monkeys with saline or ketamine injection. Ketamine injection lowers and flattens the curve of temporal weights, consistent with the lowered E/I circuit model. Errorbars in (A) indicate the standard error mean, in all other panels errorbars indicate the standard error.
Figure 8—figure supplement 1
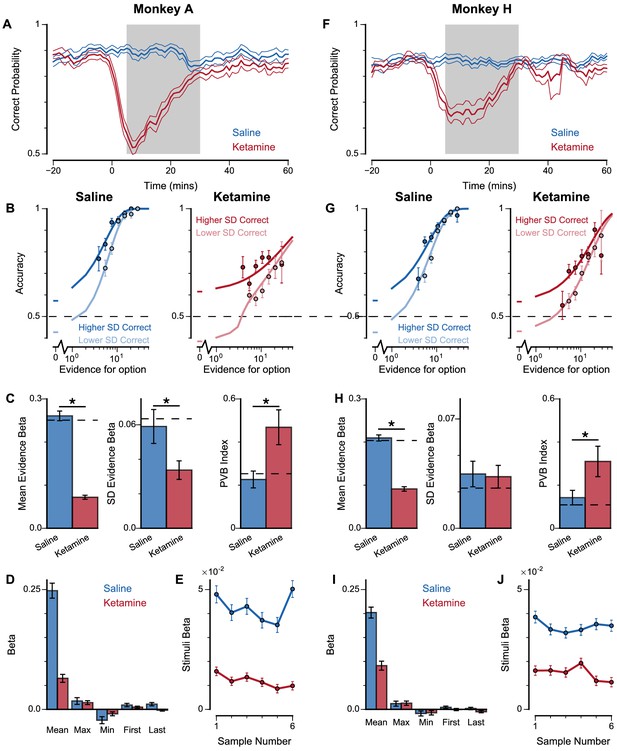
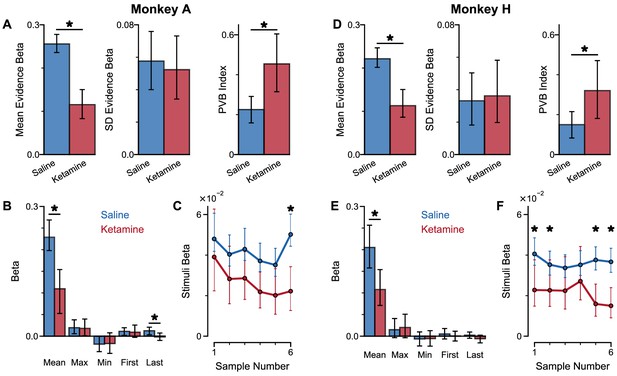
Extra information on ketamine experiments, separated by subjects.
(A) Mean percentage of correct choices across sessions made by Monkey A relative to the injection of ketamine (red) or saline (blue). (B) The psychometric function of Monkey A when either the ‘Lower SD’ or ‘Higher SD’ streams are correct with saline (left) or ketamine (right) injection. (C) Ketamine injection impairs the behaviour of Monkey A, in a manner consistent with the prediction of the lowered E/I circuit model. Dashed lines indicate pre-injection values in each plot. (Left) The regression coefficient for mean evidence, under injection of saline or ketamine. Ketamine significantly reduces the coefficient (permutation test p<1×10−6), reflecting a drop in choice accuracy. (Middle) The regression coefficient for evidence standard deviation, under injection of saline or ketamine. Ketamine significantly reduces the coefficient (permutation test p=4.98×10−3), but to a lesser extent than that of the mean evidence regression coefficient. (Right) Ketamine increases the PVB index (permutation test p=1.16×10−3), consistent with the model prediction of the lowered E/I circuit. (D) The regression model using mean, maximum, minimum, first, and last evidence values of each of the left and right streams as regressors, under injection of saline or ketamine. Each bar shows the average of the left and right regressors of the corresponding variable. Ketamine injection does not alter decision-making strategies. (E) The regression weights of stimuli at different time-steps, for Monkey A with saline or ketamine injection. Ketamine injection lowers and flattens the curve of temporal weights, consistent with the lowered E/I circuit model. (F–J) Same as (A–E) but for Monkey H. (H) Ketamine significantly reduces the regression coefficient for mean evidence (permutation test p<1×10−6), does not significantly reduce the regression coefficient for evidence standard deviation (permutation test p=0.871), and significantly increases the PVB index (permutation test p=5.92×10−3). All errorbars indicate the standard error.
Figure 8—figure supplement 2
Behavioural effects of ketamine on the pro-variance bias and temporal weightings are not explained by lapsing.
Results from Figure 8—figure supplement 1 are replicated with an extended model which included a lapse term. (A) Ketamine injection impairs the behaviour of Monkey A, in a manner consistent with the prediction of the lowered E/I circuit model. (Left) The coefficient for mean evidence, under injection of saline or ketamine. Ketamine significantly reduces the coefficient (permutation test, p<0.0001) reflecting a drop in choice accuracy. (Middle) The coefficient for evidence standard deviation, under injection of saline or ketamine. Ketamine does not significantly reduce the coefficient (permutation test, p=0.636). (Right) Ketamine increases the PVB index (permutation test, p=0.0006), consistent with the model prediction of the lowered E/I circuit. (B) The regression model using mean, maximum, minimum, first, and last evidence values of each of the left and right streams as regressors, under injection of saline or ketamine. Each bar shows the average of the left and right regressors of the corresponding variable. Ketamine injection does not alter decision-making strategies. Black asterisks denote a significant difference between saline and ketamine conditions at the respective regressor (permutation test, p<0.05). (C) The weights of stimuli at different time-steps, for Monkey A with saline or ketamine injection. Ketamine injection lowers the curve of temporal weights, consistent with the lowered E/I circuit model. Black asterisks denote a significant difference between saline and ketamine conditions at the respective sample number (permutation test, p<0.05). (D–F) Same as (A–C) but for Monkey H. (D) Ketamine significantly reduces the coefficient for mean evidence (permutation test, p<0.0001), does not significantly reduce the coefficient for evidence standard deviation (permutation test, p=0.731), and significantly increases the PVB index (permutation test, p=0.0056). All errorbars denote the 95% confidence interval generated through a bootstrap procedure.
Figure 8—figure supplement 3
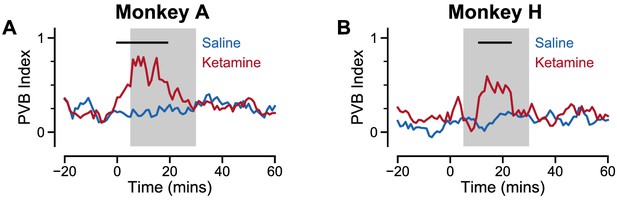
Time course of ketamine’s influence on pro-variance bias.
(A) The time course of the pro-variance bias index (PVB) is shown for Monkey A. The PVB index is significantly raised for around 20 min following ketamine administration (red). The black horizontal bar at the top of the graph denotes a significant difference between saline (blue) and ketamine conditions at the respective time points (cluster-based permutation test, p=0.0080; see Materials and methods). (B) As in (A), except for Monkey H (cluster-based permutation test, p=0.0332).
Figure 8—figure supplement 4
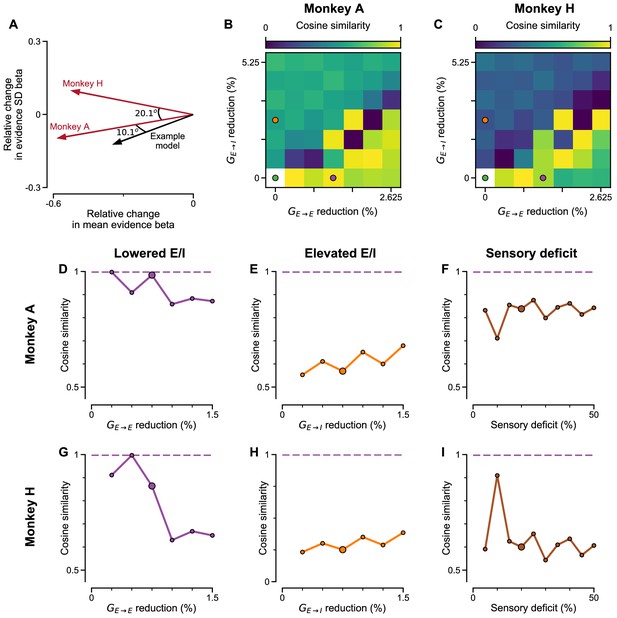
Cosine similarity of various perturbation effects in the circuit model, to the effect of ketamine injections on monkey behaviour.
(A) Schematic of the similarity measure. The effect of ketamine perturbation to monkey choice behaviour (with lapse rate accounted for) is represented as the relative change in regression coefficients for mean evidence and evidence SD of monkey under ketamine vs saline (red arrows), and similarly for perturbed models vs control circuit model. Cosine similarity is the cosine of the angle between them, and measures the similarity between distinct perturbations. The angle between the vectors of Monkey A and H is 20.1o, corresponding to a cosine similarity value of 0.94. The example model perturbation (black arrow) with weak NMDA-R hypofunction on excitatory neurons (purple dot in B,C) has good cosine similarity and Euclidean distance to the ketamine effect in both monkeys (see B-D,G, Figure 8—figure supplement 5). (B) Circuit models with various degrees of NMDA-R hypofunction on excitatory () and inhibitory () neurons are considered. In each case, the regression coefficients of mean evidence and evidence standard deviations are compared to that of the control circuit model. The direction of alteration in each perturbed model, in the 2-dimensional space of mean evidence and evidence standard deviation betas, is compared to the direction of alteration by ketamine injection to Monkey A choice behaviour. A higher cosine similarity means the relative extent (and direction) of alteration, to the regression coefficients of mean evidence and evidence standard deviation, is more similar between the perturbations in the circuit model and the monkey data. Note that the lower left corner point (i.e. the control model) is marked white to clarify cosine similarity is undefined at that point. The green, purple, and orange dots respectively denote the control, lowered E/I, and elevated E/I circuit models used in Figure 7. (C) Same as (B) but with comparisons made with Monkey H choice behaviour. (D) Circuit models with varying degrees of NMDA-R hypofunction on excitatory neurons () are considered. In each case, the cosine similarity between the perturbation vector in the model and Monkey A data are compared, in the same manner as (B). The large dot denotes the perturbation strength used in the lowered E/I model in Figure 7. Note that cosine similarity is undefined at the point with no perturbation (i.e. the control model). (E) Same as (D) but with various degrees of NMDA-R hypofunction on inhibitory neurons () in the circuit model. The large dot denotes the perturbation strength used in the elevated E/I model in Figure 7. (F) Same as (D) but with various degrees of sensory deficits in the circuit model. The large dot denotes the perturbation strength used in the sensory deficit model in Figure 7. Purple dashed lines indicate the largest cosine similarity between the ketamine effect on Monkey A and any model perturbations across (D–F) (which is achieved by a lowered E/I model). (G–I) Same as (D–F) but with comparisons made with Monkey H choice behaviour.
Figure 8—figure supplement 5
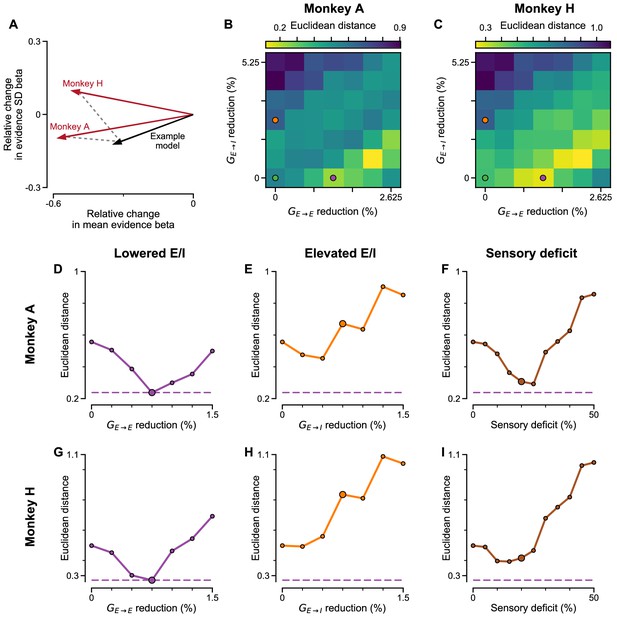
Euclidean distance of various perturbation effects in the circuit model, to the effect of ketamine injections on monkey behaviour.
(A) Schematic of the dissimilarity measure. The effect of ketamine perturbation to monkey choice behaviour (with lapse rate accounted for) is represented as the relative change in regression coefficients for mean evidence and evidence SD of monkey under ketamine vs saline (red arrows), and similarly for perturbed models vs control circuit model. The Euclidean distance between the vectors measures the dissimilarity between distinct perturbations. The example model perturbation (black arrow) with weak NMDA-R hypofunction on excitatory neurons (purple dot in B,C), has good cosine similarity and Euclidean distance to the ketamine effect in both monkeys (see B-D,G, Figure 8—figure supplement 4). (B) Circuit models with various degrees of NMDA-R hypofunction on excitatory () and inhibitory () neurons are considered. In each case, the regression coefficients of mean evidence and evidence standard deviations are compared to that of the control circuit model. The direction of alteration in each perturbed model, in the 2-dimensional space of mean evidence and evidence standard deviations, is compared to the direction of alteration by ketamine injection to Monkey A choice behaviour. A smaller Euclidean distance means the relative extent (and direction) of alteration, to the regression coefficients of mean evidence and evidence standard deviation, is more similar between the perturbations in the circuit model and the monkey data. The green, purple, and orange dots respectively denote the control, lowered E/I, and elevated E/I circuit models used in Figure 7. (C) Same as (B) but with comparisons made with Monkey H choice behaviour. (D) Circuit models with varying degrees of NMDA-R hypofunction on excitatory neurons () are considered. In each case, the Euclidean distance between the perturbation vector in the model and Monkey A data are compared, in the same manner as (B). The large dot denotes the perturbation strength used in the lowered E/I model in Figure 7. (E) Same as (D) but with various degrees of NMDA-R hypofunction on inhibitory () neurons in the circuit model. The large dot denotes the perturbation strength used in the elevated E/I model in Figure 7. (F) Same as (D) but with various degrees of sensory deficits in the circuit model. The large dot denotes the perturbation strength used in the sensory deficit model in Figure 7. Purple dashed lines indicate the smallest Euclidean distance between ketamine effect on Monkey A and any model perturbations across (D–F) (which is achieved by a lowered E/I model). (G–I) Same as (D–F) but with comparisons made with Monkey H choice behaviour.
Figure 8—figure supplement 6
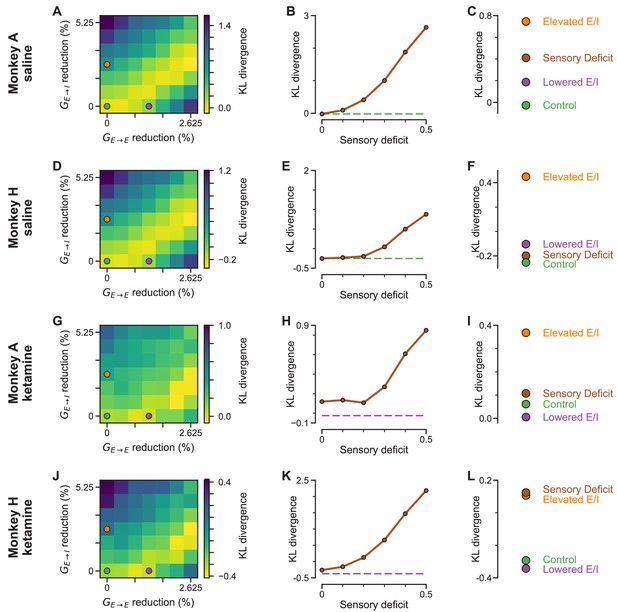
Kullback–Leibler (KL) divergence from monkey behavior with saline or ketamine to circuit models with various perturbations.
(A) KL divergence between Monkey A saline data and circuit models with various degrees of NMDA-R hypofunction on excitatory () and inhibitory () neurons. Lower KL divergence between data and model means the psychometric functions are more similar between the two. The green, purple, and orange dots respectively denote the control, lowered E/I, and elevated E/I circuit models used in Figure 7. (B) KL divergence between Monkey A saline data and circuit models with various degrees of sensory deficit. Green dashed line shows the KL-divergence between Monkey A saline data and the control model, which is the lowest among the four circuit models used in Figure 7 (see C). (C) KL divergence between Monkey A saline data and the control, lowered E/I, and elevated E/I, and sensory deficit circuit models used in Figure 7. The control model has the lowest KL divergence compared to Monkey A saline data. (D–F) Same as (A–C) but with comparisons made with Monkey H saline data. (G–I) Same as (A–C) but with comparisons made with Monkey A ketamine data. Monkey A’s empirical lapse rate is incorporated into the psychometric function of the circuit models for computing the KL divergence. (H) Purple dashed line shows the KL-divergence between Monkey A ketamine data and the lowered E/I model, which is the lowest among the four circuit models in (I). (J–L) Same as (G–I) but with comparisons made with Monkey H ketamine data.
Figure 8—figure supplement 7
Psychometric function of monkeys under ketamine injection, and circuit model with large sensory deficit.
(A) Psychometric function of Monkey A under ketamine injection, replotted from Figure 8—figure supplement 1. (B) Psychometric function of Monkey H under ketamine injection, replotted from Figure 8—figure supplement 1. (C) Psychometric function of a circuit model with 40% sensory deficit, with lapse rate fitted to Monkey A ketamine data. (D) Psychometric function of a circuit model with 40% sensory deficit, with lapse rate fitted to Monkey H ketamine data. All errorbars indicate the standard error.
Figure 8—figure supplement 8
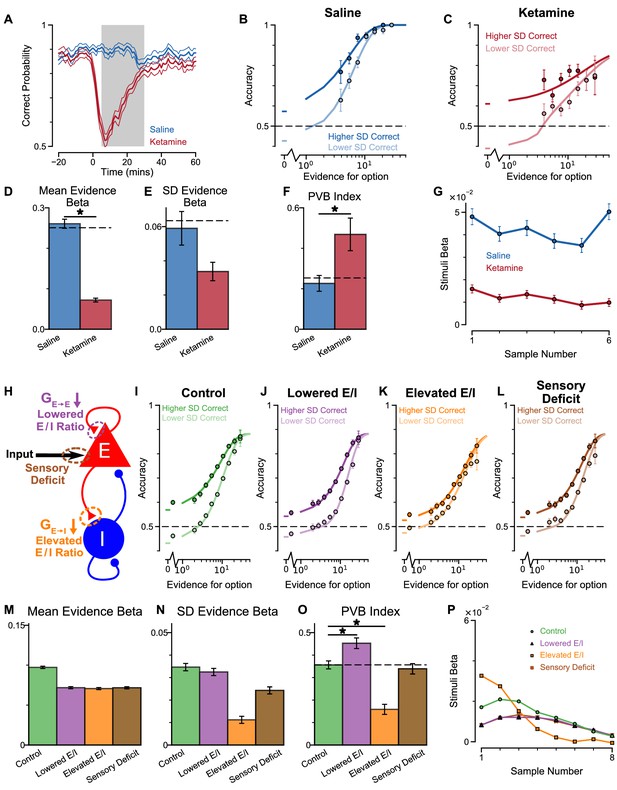
Predictions for E/I perturbations of the Spiking Circuit Model, with built-in Monkey A lapse rate, compared with Monkey A behaviour.
For each circuit model (control, lowered E/I, elevated E/I, sensory deficit), a proportion of trials are selected and the corresponding choices are randomly shuffled to one of the two choices, with the proportion determined by the empirically measured lapse rate for Monkey A. The regression weights (M–P) are then calculated from the revised choices of the circuit model using the equations without lapse rate (Equations 4 and 5) to allow direct comparison with the subject data which did not control for lapse rate in Figure 8—figure supplement 1. The choice accuracy (dots in I-L) is similarly calculated for the revised choices of the circuit model, while the psychometric fit functions (lines in I-L), which are for visualisation purposes only, are fitted using an equation which incorporated the same fixed lapse rate (Equation 12).These procedures are repeated 100 times for each circuit model, with the average values taken. (A–G) Monkey A data under saline and ketamine injection. The data are identical to that in Figure 8—figure supplement 1, and is repeated here for comparison to the model. Note that the psychometric fit function in (C) here is modified to incorporate a lapse effect for better comparison as explained above (see Materials and methods, Equation 12). (H) Model perturbation schematic. Three potential perturbations are considered: lowered E/I (via NMDA-R hypofunction on excitatory pyramidal neurons), elevated E/I (via NMDA-R hypofunction on inhibitory interneurons), or sensory deficit (as weakened scaling of external inputs to stimuli evidence).(I–L) The regular-trial choice accuracy for each of the circuit perturbations (dark colour for when the ‘Higher SD’ stream is correct, light colour for when the ‘Lower SD’ stream is correct). Note that the psychometric fit functions here are modified to incorporate a lapse effect for better comparison as explained above (see Materials and methods, Equation 12). (M–O) Regression analysis on the regular trial choices of the four models, using evidence mean and evidence variability to predict choice (see Materials and methods, Equation 5). (M) The mean evidence regression coefficients in the four models. Lowering E/I, elevating E/I, and inducing sensory deficits similarly reduce the coefficient, reflecting a drop in choice accuracy. (N) The evidence standard deviation regression coefficients in the four models. All three perturbations reduce the coefficient, but to a different extent. (O) The PVB index (ratio of evidence standard deviation coefficient over mean evidence coefficient) provides dissociable predictions for the perturbations. The lowered E/I circuit increases the PVB index relative to the control model (permutation test, p<10−5), while the elevated E/I circuit decreases the PVB index (permutation test, p<10−5). The PVB index is roughly maintained in the sensory deficit circuit (permutation test, p=0.4718). The dashed line indicates the PVB index for the control circuit, * indicates a significant difference when the PVB index is compared with the control circuit. (P) The regression weights of stimuli at different time-steps for the four models (see Materials and methods, Equation 4). All errorbars indicate the standard error.
Figure 8—figure supplement 9
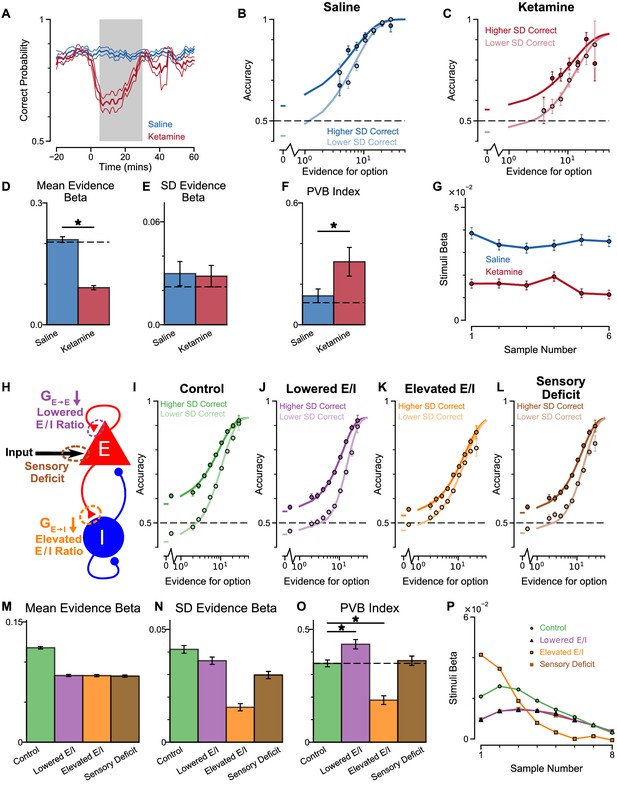
Predictions for E/I perturbations of the Spiking Circuit Model, with built-in Monkey H lapse rate, compared with Monkey H behaviour.
For each circuit model (control, lowered E/I, elevated E/I, sensory deficit), a proportion of trials are selected and the corresponding choices are randomly shuffled to one of the two choices, with the proportion determined by the empirically measured lapse rate for Monkey H. The regression weights (M–P) are then calculated from the revised choices of the circuit model using the equations without lapse rate (Equations 4 and 5) to allow direct comparison with the subject data which did not control for lapse rate in Figure 8—figure supplement 1. The choice accuracy (dots in I-L) is similarly calculated for the revised choices of the circuit model, while the psychometric fit functions (lines in I-L), which are for visualisation purposes only, are fitted using an equation which incorporated the same fixed lapse rate (Equation 12).These procedures are repeated 100 times for each circuit model, with the average values taken. (A–G) Monkey H data under saline and ketamine injection. The data are identical to that in Figure 8—figure supplement 1, and is repeated here for comparison to the model. Note that the psychometric fit function in (C) here is modified to incorporate a lapse effect for better comparison as explained above (see Materials and methods, Equation 12). (H) Model perturbation schematic. Three potential perturbations are considered: lowered E/I (via NMDA-R hypofunction on excitatory pyramidal neurons), elevated E/I (via NMDA-R hypofunction on inhibitory interneurons), or sensory deficit (as weakened scaling of external inputs to stimuli evidence).(I–L) The regular-trial choice accuracy for each of the circuit perturbations (dark colour for when the ‘Higher SD’ stream is correct, light colour for when the ‘Lower SD’ stream is correct). Note that the psychometric fit functions here are modified to incorporate a lapse effect for better comparison as explained above (see Materials and methods, Equation 12). (M–O) Regression analysis on the regular trial choices of the four models, using evidence mean and evidence variability to predict choice (see Materials and methods, Equation 5). (M) The mean evidence regression coefficients in the four models. Lowering E/I, elevating E/I, and inducing sensory deficits similarly reduce the coefficient, reflecting a drop in choice accuracy. (N) The evidence standard deviation regression coefficients in the four models. All three perturbations reduce the coefficient, but to a different extent. (O) The PVB index (ratio of evidence standard deviation coefficient over mean evidence coefficient) provides dissociable predictions for the perturbations. The lowered E/I circuit increases the PVB index relative to the control model (permutation test, p<10−5), while the elevated E/I circuit decreases the PVB index (permutation test, p<10−5). The PVB index is roughly maintained in the sensory deficit circuit (permutation test, p=0.3817). The dashed line indicates the PVB index for the control circuit, * indicates a significant difference when the PVB index is compared with the control circuit. (P) The regression weights of stimuli at different time-steps for the four models (see Materials and methods, Equation 4). All errorbars indicate the standard error.
Author response image 1
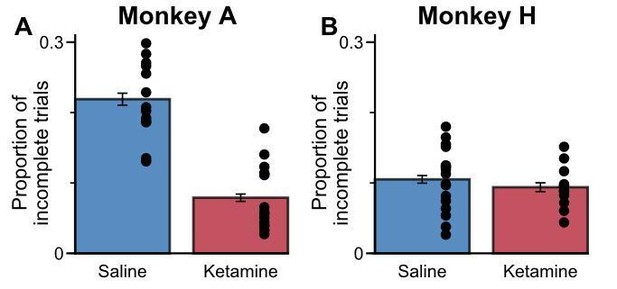
Animals rarely fail to complete trials when administered with ketamine.
The proportion of incomplete trials that occurred between 5 minutes and 30 minutes relative to drug administration. Errorbars indicate the standard error, each dot represents an individual session. Monkey A counterintuitively completed a higher proportion of trials when administered with ketamine, as this appeared to reduce his slightly stronger tendency to break central fixation early in order to directly view the stimuli. For Monkey H, the proportion of incomplete trials was relatively uninfluenced by ketamine.
Author response image 2
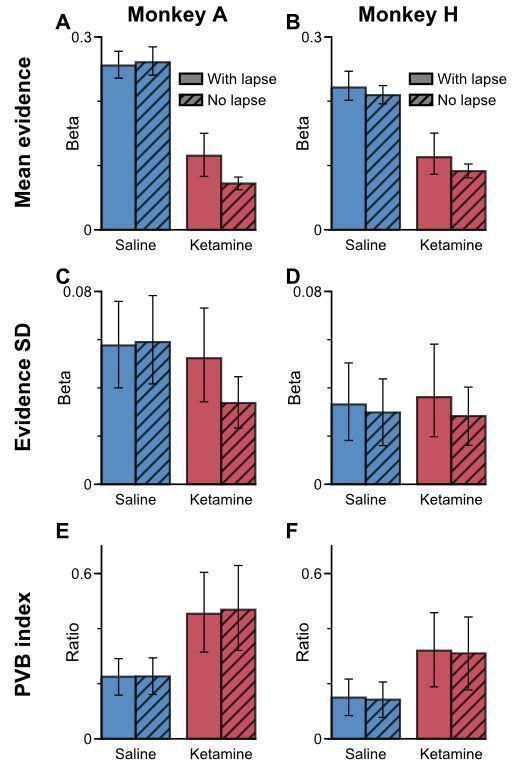
Incorporating a lapsing parameter does not greatly influence coefficients from the original logistic model for the PVB analysis.
(A) The mean evidence regression coefficient under saline (blue) and ketamine (red) under logistic regression with (no hatches) or without (hatched) a lapse term, using Monkey A data. (B) Same as (A) but using Monkey H data instead. (C-D) Same as (A-B) but for the evidence standard deviation regression coefficient instead. (E-F) Same as (A-B) but for PVB index instead. Note that while both mean evidence and evidence standard deviation regression coefficients under ketamine injection vary with or without the lapse term, the PVB index is stable to the lapse term. All errorbars denote the 95% confidence interval generated through a bootstrap procedure.
Tables
Author response table 1
| Condition | Variable | Description |
|---|---|---|
| “Select Higher” | mean(L) | Average height of the 8 bars on the left side of the screen |
| “Select Higher” | mean(R) | Average height of the 8 bars on the right side of the screen |
| “Select Higher” | std(L) | Standard deviation of the heights of the 8 bars on the left side of the screen |
| “Select Higher” | std(R) | Standard deviation of the heights of the 8 bars on the right side of the screen |
| “Select Lower” | mean(L) | Average of (100 – Bar Height) for the 8 stimuli on the left side of the screen |
| “Select Lower” | mean(R) | Average of (100 – Bar Height) for the 8 stimuli on the right side of the screen |
| “Select Lower” | std(L) | Standard deviation of (100 – Bar Height) for the 8 stimuli on the left side of the screen |
| “Select Lower” | std(R) | Standard deviation of (100 – Bar Height) for the 8 stimuli on the right side of the screen |
Author response table 2
| Authors | Journal | Intramuscular Ketamine Doses Used |
|---|---|---|
| (M. Wang, Yang et al., 2013) | Neuron | 0.5-1.5 mg/kg |
| (Blackman, Macdonald et al., 2013) | Neuropsychopharmacology | 0.32–0.57 mg/kg |
| (Ma, Skoblenick et al., 2015) | Journal of Neuroscience | 0.4 mg/kg |
| (Ma, Skoblenick et al., 2018) | Journal of Neuroscience | 0.4 – 0.7 mg/kg |
| (Shen, Kalwarowsky et al., 2010) | Journal of Neuroscience | 0.25 – 1 mg/kg |
| (K. J. Skoblenick, Womelsdorf et al., 2016) | Cerebral Cortex | 0.4 mg/kg |
| (K. Skoblenick and Everling, 2014) | Journal of Cognitive Neuroscience | 0.4 mg/kg |
| (K. Skoblenick and Everling, 2012) | Journal of Neuroscience | 0.4 – 0.8 mg/kg |
| (Taffe, Davis et al., 2002) | Psychopharmacology | 0.3- 1.7 mg/kg |
| (Condy, Wattiez et al., 2005) | Biological Psychiatry | 0.2 – 1.2 mg/kg |
| (Stoet and Snyder, 2006) | Neuropsychopharmacology | 0.07 – 1 mg/kg |
Additional files
-
Supplementary file 1
Difference in log-likelihood of Full regression model (mean, SD, max, min, first, last of evidence values; Equation 6 in Materials and methods) vs reduced model, for each monkey and the circuit model.
Log-likelihood values were calculated using a cross-validation procedure (see Materials and methods). Column label refers to the removed regressor. Positive values indicate the full regression model performs better. Values depend on the number of completed trials, which differed both between subjects and the circuit model. For both monkeys and the circuit model, mean evidence is clearly the most important driver of choice behaviour, followed by first and last evidence samples which reflects the primacy bias. Finally, evidence standard deviation (SD) has a stronger effect than maximum and minimum evidence samples (Max and Min).
- https://cdn.elifesciences.org/articles/53664/elife-53664-supp1-v3.docx
-
Supplementary file 2
Difference in log-likelihood of regression models including either evidence standard deviation (SD) or both maximum and minimum evidence (Max and Min) as regressors, for each monkey and the circuit model.
Log-likelihood values were calculated using a cross-validation procedure (see Materials and methods). Column label refers to the regressors additional to either SD or Max and Min. Positive values indicate the regression model with SD performs better than that with Max and Min. Values depend on the number of completed trials, which differed both between subjects and the circuit model. Regardless of whether first and last evidence sample regressors are included, the models with standard deviation of evidence have higher log-likelihoods than the models with maximum and minimum evidence samples, indicating a better explanation of the data by standard deviation than by maximum and minimum evidence samples.
- https://cdn.elifesciences.org/articles/53664/elife-53664-supp2-v3.docx
-
Supplementary file 3
Increase in log-likelihood of various regression models (regressors in column labels) due to inclusion of evidence standard deviation as a regressor, for each monkey and the circuit model.
Log-likelihood values were calculated using a cross-validation procedure (see Materials and methods). Values depend on the number of completed trials, which differed both between subjects and the circuit model. Positive values across the table indicates the evidence standard deviation regressor robustly improves model performance for all models examined.
- https://cdn.elifesciences.org/articles/53664/elife-53664-supp3-v3.docx
-
Supplementary file 4
Difference in log-likelihood of regression models including either evidence standard deviation (SD) or both maximum and minimum evidence (Max and Min) as regressors, for each monkey with saline or ketamine injection.
Log-likelihood values were calculated using a cross-validation procedure (see Materials and methods). Column label refers to the regressors additional to either SD or Max and Min. Positive values indicate the regression model with SD performs better than that with Max and Min. Values depend on the number of completed trials, which differed across conditions. Regardless of whether first and last evidence sample regressors are included, the models with standard deviation of evidence have higher log-likelihoods than the models with maximum and minimum evidence samples, indicating a better explanation of the data by standard deviation than by maximum and minimum evidence samples. In particular, under ketamine injection, monkeys did not switch their strategy to primarily use maximum and minimum evidence samples (over standard deviation of evidence) to guide their choice.
- https://cdn.elifesciences.org/articles/53664/elife-53664-supp4-v3.docx
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/53664/elife-53664-transrepform-v3.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
A circuit mechanism for decision-making biases and NMDA receptor hypofunction
eLife 9:e53664.
https://doi.org/10.7554/eLife.53664
