Inhibition stabilization is a widespread property of cortical networks
- NIMH Intramural Program, National Institutes of Health, United States
- Department of Neurobiology, Duke University, United States
Figures
Figure 1 with 2 supplements
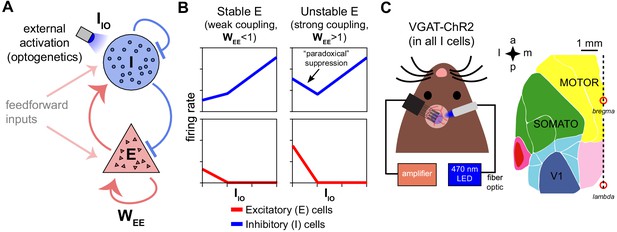
Model predictions of excitatory and inhibitory responses to inhibitory stimulation.
(A) Schematic of model, showing connections between excitatory (E) and inhibitory (I) neuron populations. (, a measure of the strength of E-E connections, is the key parameter controlling non-ISN vs. ISN operation, see model discussion in Results.) (B) Predictions for average neural responses with weak recurrent coupling (left) and strong coupling (right), when inhibitory cells are externally stimulated (). (C) Schematic of experiment. Extracellular recordings made in visual (V1), primary somatosensory (SOMATO), and motor/premotor cortices (see Figure 1—figure supplement 2 for electrode locations; a: anterior, p: posterior, m: medial, l: lateral) while optogenetically stimulating inhibitory cells at the recording site in awake VGAT-ChR2 animals.
Figure 1—figure supplement 1
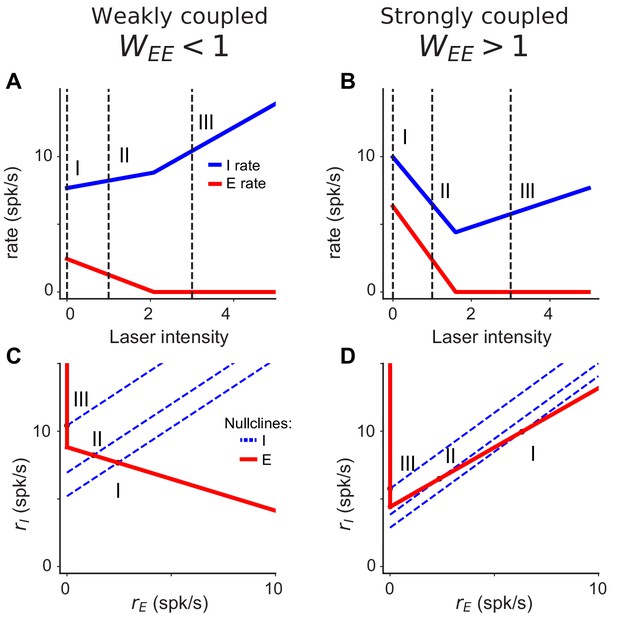
Nullclines characterizing the network response at different levels of inhibitory drive.
(A–B) Firing rate of E (red) and I (blue) populations computed from Equation 1 as a function of laser intensity when the excitatory sub-network is stable (A, ; weak coupling) or unstable (B, , strong coupling). As described in main text, inhibitory cells increase firing rate at high laser intensities in both networks. Differences are seen at lower laser intensities, where the inhibition stabilized network () responds paradoxically. (C–D) Differences in inhibitory responses are seen in the corresponding nullclines (defined as the stationary solutions of the two lines of Equation 1) For (C), at low laser intensity (I), the excitatory (red) and the inhibitory (blue) nullclines intersect at a nonzero value of (which represents the stationary point of the network). Increasing the laser intensity shifts the inhibitory nullcline to position (II) and produces a new intersection point with larger and lower . At high laser intensities (III), the two nullclines intersect at equal to zero and the corresponding value increases with the laser intensity. For (D), when the laser intensity increases from (I) to (II), both the stationary value of and decrease. This happens because the excitatory nullcline is an increasing function of , a property which appears when that the excitatory population is unstable (Tsodyks et al., 1997). At high laser intensity (III), the excitatory population is silent and stable, both the excitatory and inhibitory nullclines behave as in the case, and increasing the laser intensity increases the inhibitory rate.
Figure 1—figure supplement 2
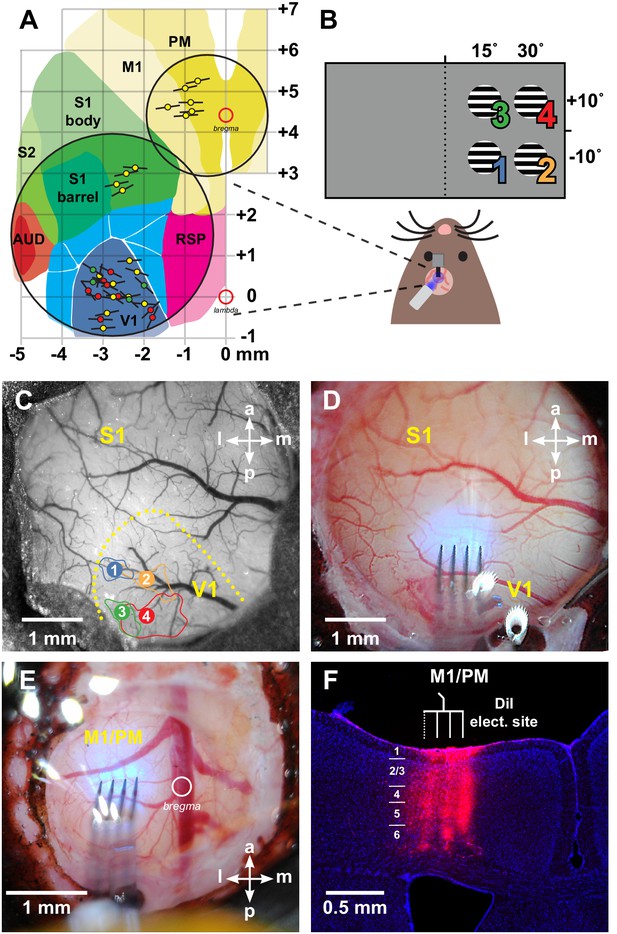
Locations of recording sites.
(A) Schematic of all physiology probe placements in the visual, somatosensory, and motor cortices (black lines give approximate extent of shanks on the 4-shank probes; colored circles signify experiment types: VGAT-ChR2: yellow; viral PV-Cre;AAV-FLEX-ChRonos: red; transgenic PV-Cre;ReaChR: green). V1: primary visual (Allen notation: VISp); RSP: retrosplenial; AUD: auditory areas; S1: primary somatosensory (SSp); S2: secondary somatosensory (SSs); M1: primary motor (MOp), PM: premotor (MOs). Coordinates are in millimeters relative to lambda and bregma (open red circles). Area boundaries drawn from Allen Mouse Brain Connectivity Atlas (Oh et al., 2014). (B) Schematic of hemodynamic intrinsic-signal optical imaging (IOI) for retinotopic mapping of V1. Hemodynamic responses were measured to upward-drifting square wave gratings (2 Hz, 0.1 cycles/°) masked with a circular boundary (10° diameter) at four locations in the right monocular field of view. (C) Picture of a large-diameter (5 mm) cranial window allowing access to the visual and somatosensory cortices. Yellow outline: estimated edge of V1 via retinotopic responses; colored numbers: centroid of IOI response corresponding to the stimulus positions in panel B; solid lines of the same colors: areas yielding responses within 50% of peak response. (D) Example physiology probe placement and blue LED overlap for optogenetic stimulation in V1. (E) Picture of a smaller-diameter (3 mm) window implant allowing access to the motor cortex. (F) Histological section showing location of electrode tracks in M1/PM. Section at 0.7 mm anterior to bregma. Blue: DAPI. Red: DiI deposited on electrodes before insertion.
Figure 2 with 8 supplements
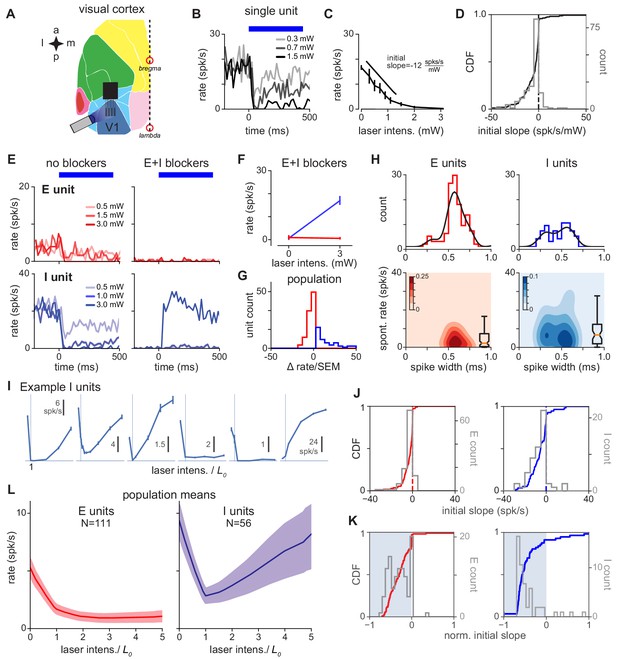
V1 response is consistent with inhibition stabilization.
(A) Schematic of experiment, showing recordings/stimulation in V1. a: anterior, p: posterior, l: lateral, m: medial. V1 recording locations, and intrinsic signal imaging to define V1, are shown in Figure 1—figure supplement 2. (B) Example recorded unit; greater laser power produces greater firing rate suppression. Blue bar: duration of constant-power laser pulse. (C) Average firing rate of example recorded unit (rate is steady-state firing rate, over last 300 ms of laser stimulus). Suppression is quantified via initial slope of firing rate vs laser intensity (Materials and methods). (D) Distribution of initial slopes for all recorded units. (E) Example cell responses without (left) and with (right) blockers. Top: Cell classified as excitatory; does not respond to laser in presence of blockers (CNQX, APV, bicuculline; Materials and methods). Bottom: Cell classified as inhibitory; increases firing rate to laser in presence of blockers. (F) Firing rates for units in (E) in presence of blockers; inhibitory cell (blue) shows a large positive change. (G) Distribution of firing rate changes to laser stimulus with blockers. Red: E-classified units; blue: I-classified units. (H) Spontaneous firing rates and waveform width (time from waveform first local minimum to first local maximum) for units classified as E and I via the method in panel G. (I) Example inhibitory units. x-axis: normalized laser intensity. Normalization: to account for variations in tissue optical properties across recording days, we combined data by fitting a piecewise-linear function to the average inhibitory response for each day to find the minimum for that day (: always between 0.3 and 2.7 mW, see Figure 2—figure supplement 6) and rescaling the laser intensity so (vertical lines). Most units (91%) show initial suppression; see J,K for initial slopes for all units. (J) Distribution of initial slopes for units classified as E (red, left) and I (blue, right). (K) Distribution of normalized initial slopes (), to more clearly show small slopes, for units classified as E and I. Several excitatory cells with very low firing rates in the no-blocker case have near-zero normalized slopes. (L) Average population response for units classified as E and I. Inhibitory cells show a prominent paradoxical effect. Errorbars: ±1 SEM (throughout figures, unless otherwise noted).
Figure 2—figure supplement 1
Unit response to light as a function of depth.
Each plot shows the average of all inhibitory units recorded from V1 in VGAT-ChR2 experiments (data as in Figure 2) without blockers present. Panels show the average unit firing rate as a function of laser intensity at sites of different depths. The recording probes have eight sites per shank (four shanks, 32 total sites) with 100 µm spacing between sites. Inhibitory neurons on the shallowest four sites (left) show strong initial suppression to laser stimulation, and at higher laser power show increases in firing rate to stimulation. Neurons from deeper sites show suppression, but do not show a clear transition to increased firing rates, even at maximum laser intensity. This is consistent with the fact that the laser intensity experienced by neurons decays with depth due to scattering and absorption. Note that we normalize laser powers to compare excitation power across experimental sessions; this process finds just one scaling factor () for all neurons and all sites for each experimental day, and the non-normalized data are shown in Figure 2—figure supplement 6. Errorbars: SEM across units.
Figure 2—figure supplement 2
Experimental results are robust to quality of unit isolation.
(A) Signal-to-noise ratio (Kelly et al., 2007) of single (black) and multi (gray) units. Single units are classified manually (blind to initial slope) based on waveform principal component separation from noise and other units, change in waveform separation over time, and inter-spike-interval distribution. As expected, classified single units have a larger SNR (single-unit E median SNR: 3.97, I median 2.83) than multi-units. Units classified as multi-units were excluded from all further analysis and are shown here only for comparison purposes. (B) Population response computed in a subset of SU with SNR higher than the threshold indicated in title. As the constraint becomes more stringent (left to right), the number units used decreases, and the paradoxical effect is preserved (for all panels, initial slope median is significantly negative: all except bottom right: ; one-sided Mann-Whitney U test). Additional evidence that the paradoxical effect is not dependent on our unit isolation comes from the fact that the PV-Chronos recordings were conducted with identical experimental procedures, and show no average paradoxical effect (see Results and Figure 6).
Figure 2—figure supplement 3
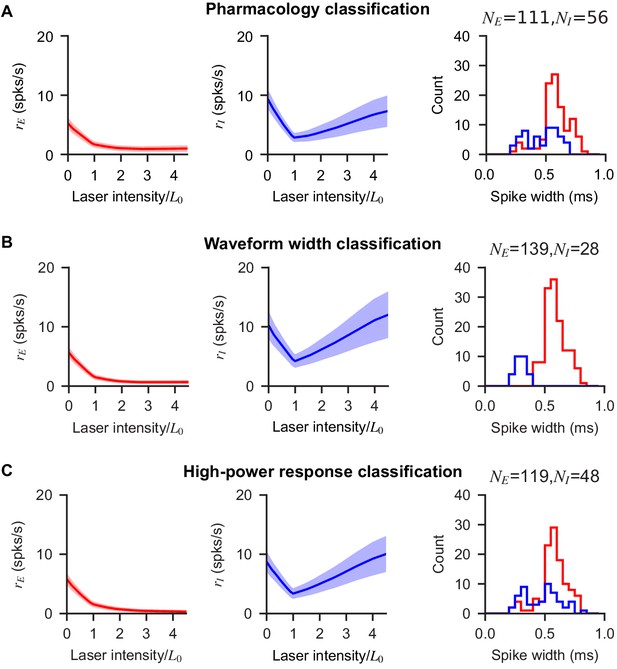
Paradoxical effects in V1 are preserved when inhibitory units are classified via pharmacology, via waveform width, and via response at high laser power.
Population response in V1 of excitatory and inhibitory cells as defined by: response with blockers (A), waveform width (B), and firing rate increase at high laser intensity (C). Figure 2 of the main text uses the classification in shown in (A), but a similar population response results using the two alternative methods of classification. (B) Units are classified as inhibitory if their waveform width is less than 0.45 ms, a value determined by the bimodal distribution observed in the population (left panel). (C) Units are classified as inhibitory if their firing at maximum laser intensity ( in the figure) is one SEM larger than their firing at (the minimum inhibitory network response).
Figure 2—figure supplement 4
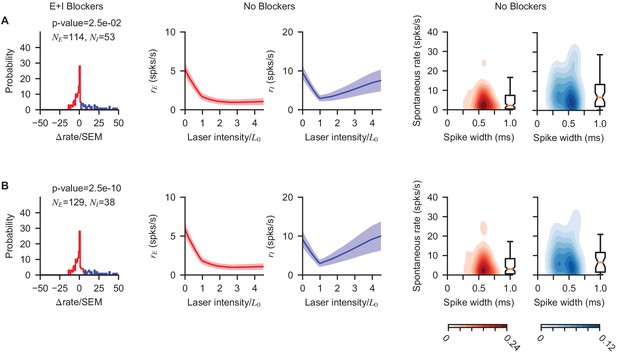
Paradoxical V1 inhibitory response does not depend on statistical E/I classification threshold.
The pharmacological classification method (based on firing rate increase to optogenetic stimulation when E+I blockers had been applied; Figure 2) is robust to choice of classification threshold applied to that firing rate change. In addition, Figure 2—figure supplement 2 shows paradoxical effect is preserved as waveform isolation via SNR is varied; Figure 2—figure supplement 5 shows potential waveform drift over time does not affect results. (A) Left column, distribution of response slopes shown with a permissive classification threshold (; to make the test two-tailed we used ; Welch’s t-test allowing unequal variances). Middle two columns: resulting average response to stimulation. Right two columns: distribution of spontaneous rates and waveform widths. (B) Same, but for a more restrictive classification threshold (). Decreasing the threshold reduces the number of units classified as inhibitory, (13 units re-classified as excitatory once the more stringent threshold is applied), but does not modify the conclusions of the main text; in particular paradoxical inhibitory modulation is preserved.
Figure 2—figure supplement 5
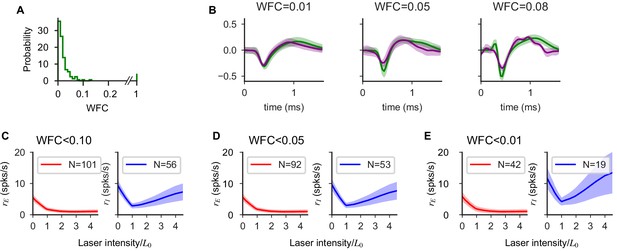
Waveform drift has no qualitative effect on population response.
(A) Distribution of relative waveform change index (WFC). WFC is defined as, for every unit, the quantity
(14)
where the waveform and its variance are given by and, and indexing the blocker, no-blocker cases. ranges over time samples of the recorded waveforms (45 samples/waveform, ms, 30 kHz acquisition rate). Equation 14 measures the relative change in waveform of a unit before and after the addition of blockers. Note that a small number of units did not spike after the addition of blockers (WFC = 1, N = 9); these could either be excitatory units that become silent, or units that drifted substantially during the recording. (B) Example single unit before (green) and after (purple) the addition of synaptic blockers. (C-E) Population response of excitatory and inhibitory cells computed using single unit selected with a threshold on the maximum waveform change. As the constraint becomes more stringent (left to right), the number units used decreases but the structure of the response is not modified and the paradoxical effect is preserved. Our waveform-sorting procedure uses a contour, fixed over time, in the 2d axis of the first two principal components (PCs) to classify units. Therefore, larger WFC values (e.g. WFC = 0.08 in B, right panel) signify some shift in waveform , despite the fact the limits of maximum waveform shift are constrained to a range of possible PC values specified by the contour. Including units that show relatively larger waveform shifts (compare D and E) does not modify our effects.
Figure 2—figure supplement 6
Reversal point of V1 inhibitory population is typically at a low laser intensity.
Nine recording sessions (panels) from V1 are shown. Dots: mean inhibitory responses (mean ± SEM) measured without blockers in the awake state. For every session, we fitted the inhibitory response to a continuous two-segment piecewise-linear function (three parameters, black lines) to infer the transition point (, black dashed lines) from ISN to non-ISN network behavior. The initial slope in all fits was negative and the second slope in all fits was non-negative (although small in three of the sessions; excluding these sessions preserved the average paradoxical effect). ranged from 0.3 to 2.7 mW, presumably due to variation in the preparation such as granulation tissue thickness; we used this value to normalize intensity for combining data from different sessions. Here, as in Figure 2, we used response with E and I blockers to classify units as E or I.
Figure 2—figure supplement 7
V1 inhibitory cell responses.
Individual inhibitory cells (dataset: VGAT-ChR2, transgenic) show some variability in response, but the large majority show paradoxical suppression. (A) Firing rates of the inhibitory cells recorded in V1 (N = 56). Each cell is indicated by a gray line connecting blue points. Only a subset (N = 6) of intensity points are shown for each cell for visual clarity. Solid blue line: mean firing rate, as in Figure 2I. Points are jittered (with a uniformly distributed random offset added to each) to show density clearly. Gray bars contain percentiles of firing rate; left gray bar: percentiles for stimulation intensity 0; right gray bar: percentiles for max intensity (4). Percentiles 25, 50, 75, and 95 are shown. (B) Same as A but for normalized firing rate (each cell’s firing rate divided by its rate at intensity zero). Some cells firing rates’ continue to rise above the maximum y-limit (3.0; chosen so that lower firing rates could be seen clearly). As intensity is increased from zero to 1 (; computed across recording sessions not across cells; Materials and methods), most inhibitory cells paradoxically decrease their firing rates, with 5 (9%) increasing. Many inhibitory cells remain suppressed even at maximum stimulation intensity. However, a substantial subset of inhibitory cells reverse their suppression above , and increase their firing rates as stimulation intensity is increased.
Figure 2—figure supplement 8
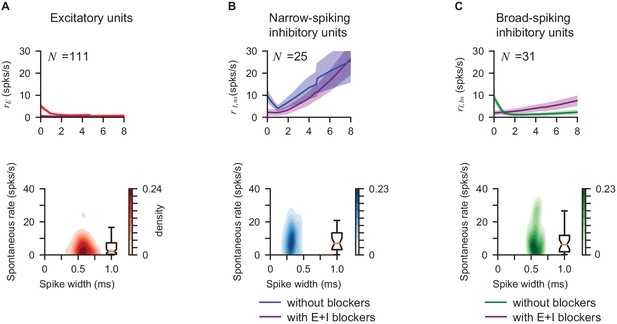
Responses of broad- and narrow-spiking V1 (VGAT-ChR2) inhibitory units.
Average rate (first row) and distribution of spontaneous rates vs. spike width (second row) of excitatory units (A, ), narrow-spiking inhibitory units (B, waveform width < 0.45ms, ), and broad-spiking inhibitory units (C, waveform width > 0.45ms, ). Corresponding average response with E+I blockers is plotted to show elevated responses with light (first row, purple). Cells are classified as E or I via pharmacological classification (as in Figure 2). The two inhibitory populations both show initial paradoxical suppression. Narrow-spiking units show a more pronounced increase in firing rate in the non-ISN (high laser power) regime. This difference seems unlikely to result from experimental differences like variation in opsin expression levels, and more likely may be generated by recurrent inhibition (i.e. narrow spiking putative basket/PV cells provide strong inhibition to wider-spiking somatostatin or other inhibitory cells, and at high laser powers PV cells suppress the wider-spiking units). In Figure 6, for both the viral PV-Chronos and transgenic PV-ReaChR experiments, we classify cells as inhibitory based on elevated response at high laser power. Consistent with the V1 VGAT-ChR2 data shown above, the cells in PV experiments classfied as inhibitory by their high-power response also have narrow waveforms on average.
Figure 3 with 1 supplement
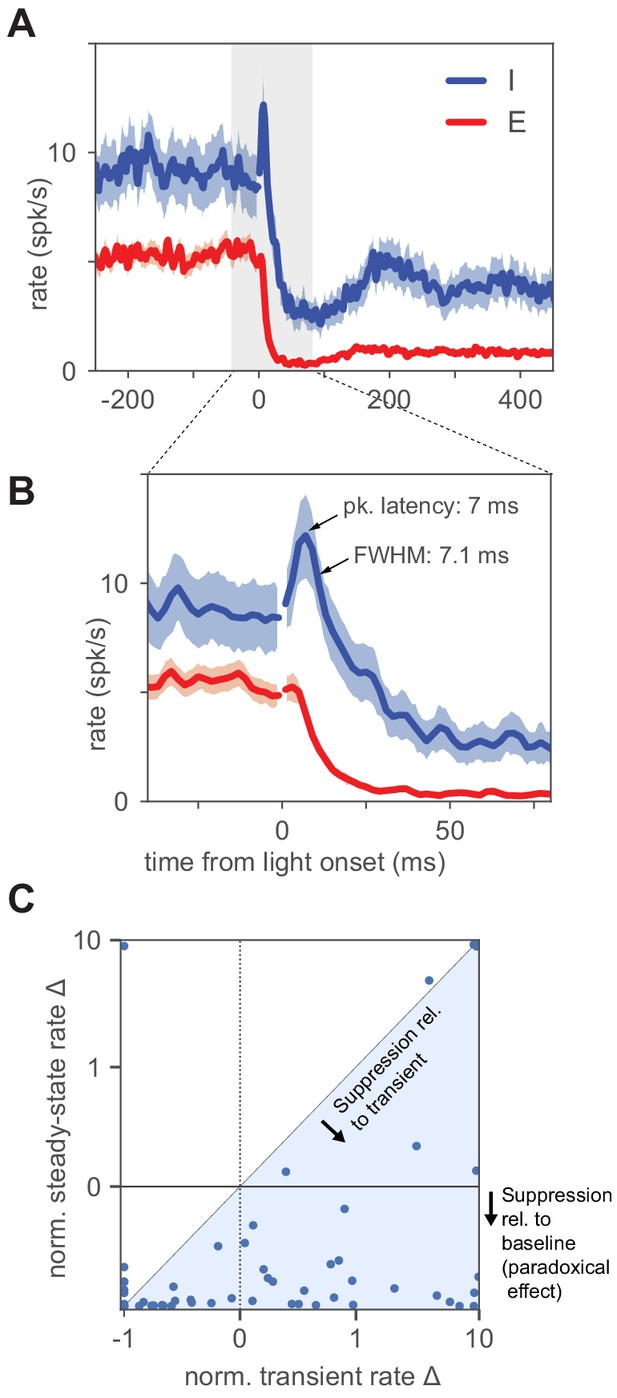
Inhibitory neurons show a small increase in firing before paradoxical suppression.
(A) Average timecourse of neural responses from units classified as excitatory (N = 111) and inhibitory (N = 56). Light pulse is constant-intensity and lasts for 800 ms (high-intensity pulse, 2.6 ; stimulation strength larger than is predicted by ISN models to produce larger transients than at , though steady-state I rates are larger than the minimum; see also Figure 3—figure supplement 1). Data from VGAT-ChR2 animals. Heavy lines: population mean rate, smoothed with a LOWESS filter. Shaded regions: SEM (Materials and methods). The onset of the light pulse produces an artifact in the 0 ms time bin; we drop spikes at that time point (broken lines, time = 0) to remove the artifact. Inhibitory neurons show a brief increase in firing before suppression, and the increase above baseline is statistically significant (inhibitory firing rates over 12 ms window after pulse are greater than a matched-duration interval before pulse, , KS test). (B) Same data as (A), enlarged to show the initial transient (time range here is indicated in (A) by gray shaded region). Inhibitory initial positive transient has peak amplitude 3.6 spk/s above baseline, latency to peak 7 ms, full width at half maximum 7.1 ms, and inhibitory rate crosses baseline into suppression at 13.1 ms. (C) Size of transient vs. size of steady-state suppression for all I units. The majority of units show steady-state paradoxical suppression relative to both baseline rate and to transient rate. y-axis: steady-state rate change (normalized to baseline; ). x-axis: normalized transient; measured from 1 to 12 ms after light onset. Units below the horizontal line at zero show paradoxical suppression; units in the blue shaded region are those whose normalized steady-state rate is lower than their normalized transient rate. A few units show a positive transient and elevated steady-state rate (upper right quadrant); these are likely inhibitory units showing non-paradoxical steady-state rate increases.
Figure 3—figure supplement 1
Many inhibitory cells show an initial transient and also steady-state paradoxical suppression.
(A) Schematic of laser intensity used here and in Figure 3. This intensity () is above the point of maximal paradoxical steady-state suppression (), but shows the initial transient (Figure 3A,B) clearly. (B) Paradoxical suppression (initial slope < 0) is seen even when selecting only the inhibitory units that show a positive initial transient (transient > 0), those units with an increase in spike rate over the interval [1,12] ms after light onset. (I: all recorded inhibitory units, N = 56). (C) Same as B, but for normalized initial slope.
Figure 4 with 2 supplements
Population response is consistent with a network with moderately strong coupling.
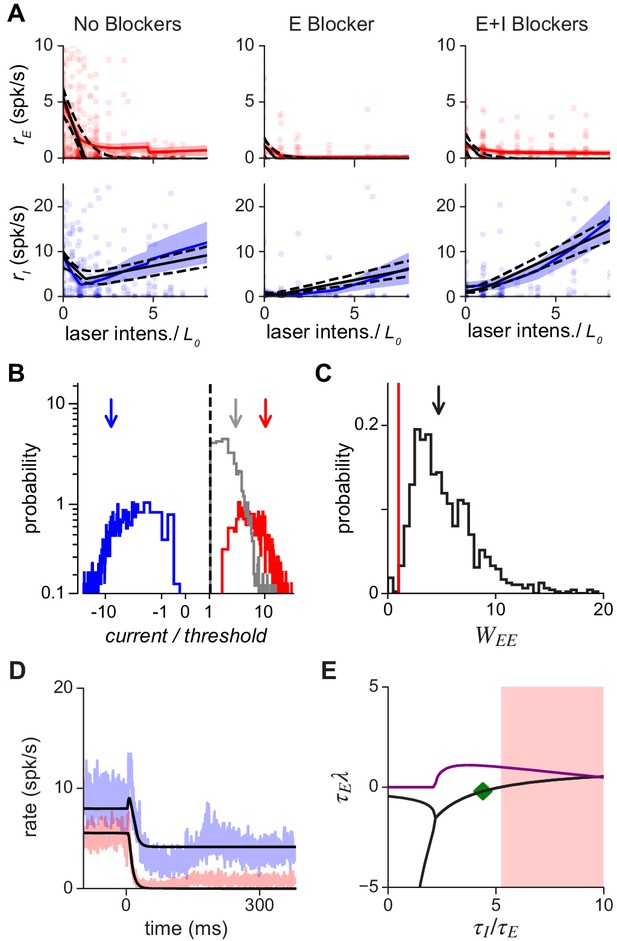
(A) Average excitatory (red) and inhibitory (blue) response measured in three conditions: without synaptic blockers, with only the excitatory blockers present, and with both E and I blockers present. Model (Equation 6) that best fits data: black continuous line; dashed: 1 s.d. obtained by bootstrap; solid red/blue lines: E/I data means; shaded region: ±1 SEM. Because we applied blockers sequentially (generating separate E and E+I blocker measurements) the number of independent observations were increased, allowing the inference of all model parameters (Materials and methods; Figure 4—figure supplement 2). Small steps in left panels (no blockers) arise because a subset of experimental days used a maximum laser intensity of . (B) Excitatory (red), inhibitory (blue), and net (gray) current influx into excitatory cells predicted by the model. Arrows: medians (over bootstrap repetitions); E: 10.9, I: −8.63; modes: E: 2.5, I: −2.7. (C) Distribution of values compatible with the data; the red line represents the transition point between the ISN () and the non-ISN () regime. Median (arrow) 4.7; mode 2.5. (D) Estimation of time constants of E and I populations. Black line shows the dynamics resulting from fitting the data (blue: I population; red: E population; shaded region ±1 SEM) with the model for the same laser power shown in Figure 3. Best-fit values are ms and ms; note that network response dynamics shows faster time constants due to recurrent network effects. The full model provides a good approximation to the dynamics even though it is constrained to simultaneously fit the time constants and the responses at different intensities. (E) Stability analysis. Real (black) and imaginary (purple) parts of the eigenvalues of the Jacobian matrix as a function of the ratio . Imaginary part (purple) greater than zero signifies the network can show damped oscillations when being driven to a new stationary point. Note that these damped oscillations are not seen in (D) because of rectification. When the real part (black) is greater than zero, the network is unstable (shaded red area).
Figure 4—figure supplement 1
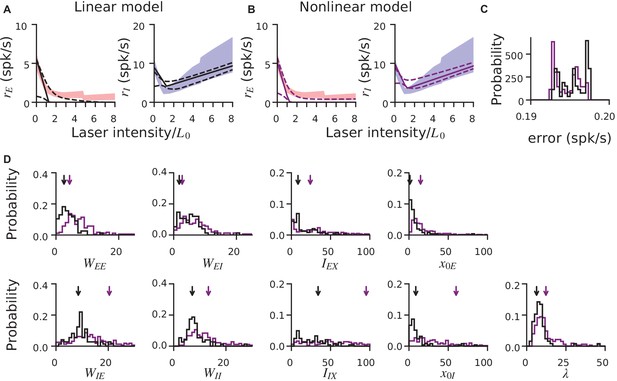
Comparison of linear and nonlinear rate models, and global optimization method.
(A–B) Similar characterizations of the V1 data are provided by linear and non-linear rate models (i.e. models with either piecewise-linear or non-linear single-cell transfer functions), even though the non-linear model has one extra parameter (which controls the transfer function nonlinearity; Materials and methods). Shaded regions: means ± 1 SEM for E (red) and I (blue) units; data is recorded from V1 of awake animals, same data set as Figures 2–4. Solid black lines: optimal (lowest-error) fit, across many optimization runs initialized with different parameter values. The lowest-error fit is the global minimum of the optimization cost (error) function. To include only plausible solutions, we retained optimzation results only where error is within 2.5% of optimal. Dashed lines: ±1 s.d. across optimization runs. (C) Error values for the two models (black: linear; purple: nonlinear). Error (units: spk/s) is the absolute difference between model and data mean, averaged over all laser intensities. (D) Parameters corresponding to solution shown in A,B. While the optimal solutions (arrows) show some differences between the two models, the distribution of parameters across runs overlaps substantially, showing the inferred network parameters are robust to the specific model used. Note that the distributions shown here are taken over optimization initialization values, in contrast to Figure 4, which shows variability of the optimal solution over bootstrap runs.
Figure 4—figure supplement 2
V1 model parameter stability shown via data bootstrap.
To examine the stability of the model fit shown in Figure 4, here we show the distribution of the parameter estimates obtained via bootstrapping (randomly resampling) the data (Materials and methods). (A) Distribution (solid lines) of the network parameters (defined by Equation 6), and corresponding medians (arrows) over all the bootstrap runs. (B) Distribution of the parameters for excitatory (red) and inhibitory (blue) blocker efficacy (left column) with corresponding measured and predicted responses (middle column, red: excitatory cells; right column, blue: inhibitory cells). Different rows correspond to different recording sessions. Shaded areas: ±1 SEM across units. The efficacy of blockers varies somewhat from day to day, justifying our use of different efficacy parameters for different recording days in the model.
Figure 5
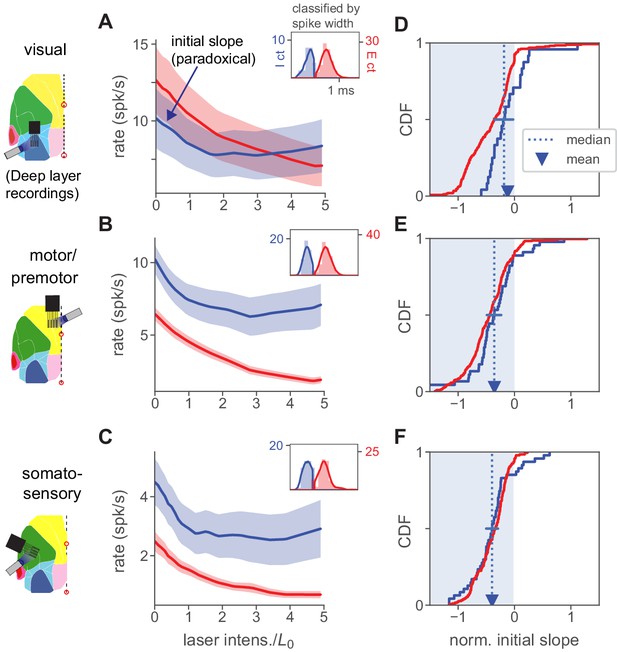
Inhibition stabilization across cortical areas.
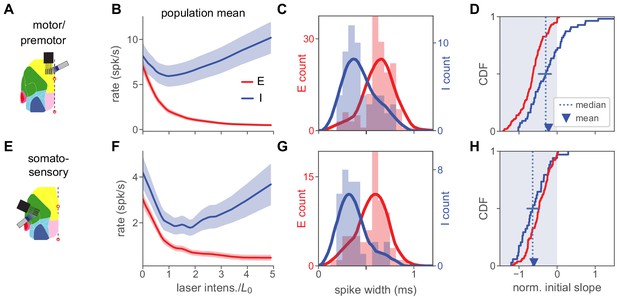
(A) Motor/premotor cortex recordings (see Figure 1—figre supplement 2 for recording locations). (B) Motor cortex population firing rates for E and I units. Initial mean response of inhibitory cells is negative, showing paradoxical suppression. Mean rate is significantly reduced (, paired t-test, rate at 0 vs rate at ). (C) Spike width distributions for E and I units. Units are classified as E or I here by response at high laser power (Materials and methods), independently of spike width, which nonetheless varies with E or I unit identity. (D) Normalized initial slope distributions for all units. Red: E. Blue: I. Both mean and median of initial slopes are negative (paradoxical). Mean I slope is negative (, t-test). Horizontal bar at I median shows 95% confidence interval calculated by bootstrap. (E–H) Same as (A–D), but for recordings from somatosensory cortex. In (G), highest red bar is truncated for visual clarity (value is 22). Mean I rate (F) is sigificantly reduced (, paired t-test). Mean I slope (H) is negative (, t-test). Horizontal bar in (H) shows 95% CI around median slope.
Figure 6 with 2 supplements
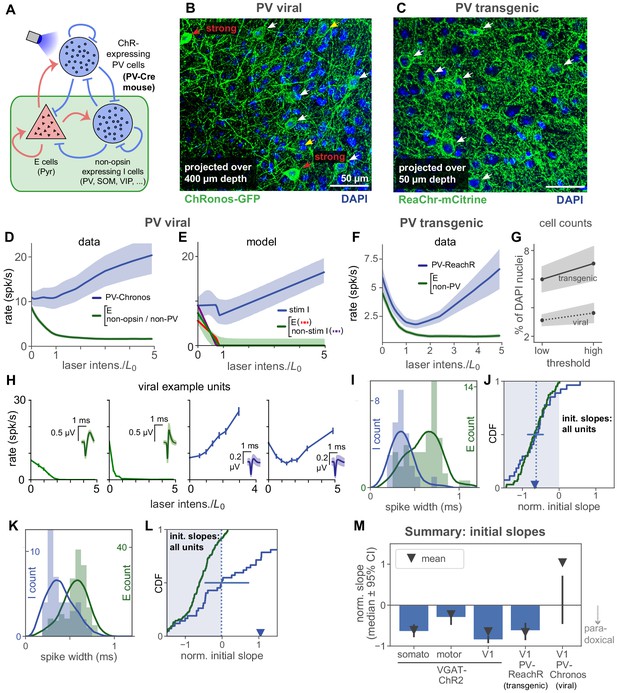
Stimulation of parvalbumin-positive inhibitory neurons shows paradoxical effects depend on number of cells stimulated.
(A) Schematic of cell populations: opsin-expressing PV cells, non-stimulated inhibitory cells (non-PV inhibitory cells: SOM, VIP, …, and non-opsin PV cells), and pyramidal (E) cells. Data are from two experiments: Viral expression of opsin (Chronos) in PV neurons (PV-Cre animals with AAV-FLEX-Chronos-GFP injections), and transgenic expression of opsin (ReaChR) in most or all PV neurons (PV-Cre;ReaChR-mCitrine). Responses shown are steady-state responses after light stimulation (Materials and methods), to avoid differences in opsin kinetics affecting results. (B,C) Histological characterization of viral (B) and transgenic (C) expression in superficial layers. Viral expression shows more variability across neurons (cf. red and white arrows), and fewer expressing cells (viral image is a projection across greater depth than transgenic). (D) Responses to stimulation with viral expression. Non-PV-Chronos (E, non-Chronos, or non-PV) cells: green (N = 152). PV-Chronos (blue) cells (N = 42, 21%), identified by responses at high laser power (Results; see Figure 2—figure supplement 3 for validation against pharmacology-based classification in V1 data). Compared to when all inhibitory cells are stimulated (VGAT-ChR2 mouse line, Figure 2), weaker paradoxical suppression is seen (blue line; mean rate is not significantly suppressed: , paired t-test between rate at 0, rate at ) as initial response slope is near zero. (E) A model with a subset of inhibitory cells stimulated (60%) can recapitulate the data in (B). Shaded region: ±1 s.d. via data bootstrap as in Figure 4. Other than splitting inhibitory population into two subsets, network parameters (Materials and methods) are as inferred in Figure 4. (F) Population responses for transgenic expression of ReaChR in PV neurons. Unlike the viral-expression data (D), the identified inhibitory cells in these experiments show paradoxical suppression; mean firing rate is significantly suppressed (, paired t-test on initial slopes). (G) Cell counts in histological sections. Solid/dotted black lines: means across two independent human counters; upper and lower gray boundaries give results from each counter. X-axis shows variation as counters were asked to use a high or low threshold for accepting an opsin positive cell. Cells were counted across 400 µm depth and are expressed (y-axis) as a percent of DAPI-positive nuclei. Transgenic expression gives about twice as many opsin expressing cells as viral expression, in addition to the differences in expression heterogeneity seen in (B–C). (H) Example viral (PV-Chronos) units show diversity of responses to stimulation. Some narrow spiking units (blue, rightmost two panels) show non-paradoxical initial increases, and some show paradoxical initial suppression. (I,J) Distribution of spike widths (I) and initial slopes (J) for experiments using transgenic PV-ReaChR (bottom). Same conventions as in Figure 5, except here colors are as shown in panel (A). (K,L) Same as (I,J) for viral expression. Although inhibitory units are classified by response at high laser power, differences in spike width are visible in both datasets. Viral mean and median slopes are zero or positive (t-test for negative mean , Mann-Whitney U for negative median ; 22/42 (53%) negative I slopes); transgenic mean and medians are negative (negative mean , negative median ; 24/27 (89%) negative I slopes). (M) Summary of mean and median inhibitory cell initial slopes for these data and data from V1, somatosensory, and motor cortex.
Figure 6—figure supplement 1
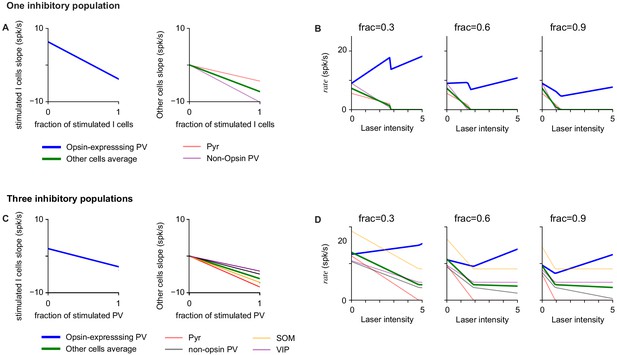
Additional analysis of inhibitory responses to partial stimulation of inhibitory population.
(A–B) Network response computed from Equation 10 for different fractions of stimulated inhibitory cells. (A) Response slope at baseline activity of different populations in the network. The response slope of stimulated cells is positive when the fraction is small, and becomes negative as the fraction increases. For these model parameters (computed from data, Figure 4), the response slope of the non-stimulated cells is negative for all fractions. (B) Responses as a function of laser intensity for different fractions of stimulated cells (from left to right: frac=0.3, 0.6, 0.9). (C–D) Results analogous to those in A-B, but obtained in a model with three inhibitory populations (representing PV, SOM, VIP Litwin-Kumar et al., 2016) as a function of the fraction of stimulated PV cells (i.e. opsin-expressing PV cells). The model structure is analogous to that of Equation 10 but with three inhibitory populations, one of which is partially stimulated. The connectivity matrix used is consistent with experimental measurements (Pfeffer et al., 2013) and is given by: if A = E and 1 if A = PV, SOM, VIP; WAPV=−1 if A = E, PV and 0 if A = SOM, VIP; WASOM=−1 if A = E, −0.5 if A = PV, 0 if A = SOM and −0.6 if A = VIP; WAVIP=0 if A = E, PV, VIP and −0.25 if A = SOM.
Figure 6—figure supplement 2
No effect of opsin kinetics on paradoxical effects.
(A) Average spike rate responses from PV-Chronos stimulation over different counting windows (300–400 ms, 400–500 ms, 500–600 ms). The overall effect is unchanged, showing that we are measuring steady-state network response, and onset and offset opsin kinetics does not affect our paradoxical effect measurements. (B) Same as A, but for PV-ReaChR recordings. Units shown here are the same as in Figure 6D,F, where the firing rates are found over the whole (300–600 ms) counting window.
Figure 7 with 1 supplement
Paradoxical inhibitory suppression is also seen in deep-layer recordings.
(A) Population average responses of deep-layer (recorded ≥500 µm from cortical surface) units, classified as inhibitory (blue) or excitatory (red) by waveform width (inset; solid line is kernel density fit to underlying histogram, expressed in units of counts on they-axes, and spike width in ms on the x-axis, see Materials and methods). Shaded area shows ± 1 SEM about mean. is defined for all units recorded in a single session based on responses to superficial-layer recordings. Initial slope of inhibitory average response is negative (paradoxical). (B,C) Same, for motor/premotor and somatosensory. (D–E) Initial slopes of all recorded units shown in A-C. Conventions as in Figure 2K. As in that panel, slopes here are normalized by baseline rate so that minimum slope is −1. Means and medians of individual inhibitory neurons’ slopes are all negative (t-test, V1 , others ) except for V1 median (blue error bar shows 95% confidence interval around median via bootstrap: upper CI, V1 0.03, motor −0.22, somato −0.33). Also, the population firing rate decrease is significant for all three areas (, except V1 , Mann-Whitney U on summed population counts, baseline vs. rate at ).
Figure 7—figure supplement 1
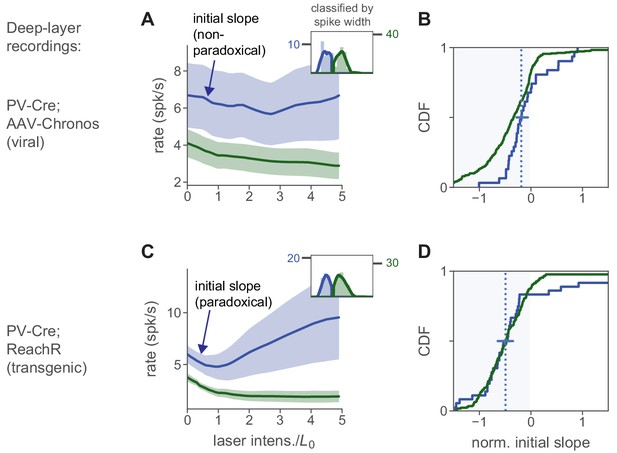
Effects of PV stim with viral vs. transgenic expression in deep-layer neurons is similar to effects in superficial layers.
(A) Deep-layer (depth ≥500 µm) units from viral transfection experiments yield no mean paradoxical effect, as in superficial-layer recordings (Figure 7). (B) Initial slopes for all recorded units: both mean and median are negative (horizontal line, 95% CI for median via bootstrap). (C–D) Deep-layer units with transgenic expression do show a mean paradoxical effect. Conventions as in Figure 7; blue indicates inhibitory cells, and green indicates combined excitatory, non-PV, and PV non-transfected neurons. As in Figure 7, these neurons are classified by waveform width. In the transgenic line (C–D), paradoxical suppression is clear, but less strong in deep layers than in superficial layers (Figure 6), a pattern we also saw with stimulation of all inhibitory cells (Figure 2, Figure 5, Figure 7). Because PV-ReaChR was stimulated with red light, we expect more direct effects of stimulation in deeper layers than with blue-light VGAT-ChR2 stimulation (Figure 7), and indeed, here a greater number of inhibitory cells show paradoxical suppression (D) than in the VGAT-ChR2 deep layer recordings from V1 (Figure 7D). Note that because we stimulate PV neurons and not all inhibitory cells, the data in this figure is not diagnostic of ISN operation, but illustrates that PV stimulation can indeed produce paradoxical effects in inhibitory neurons in deep layers.
Figure 8 with 1 supplement
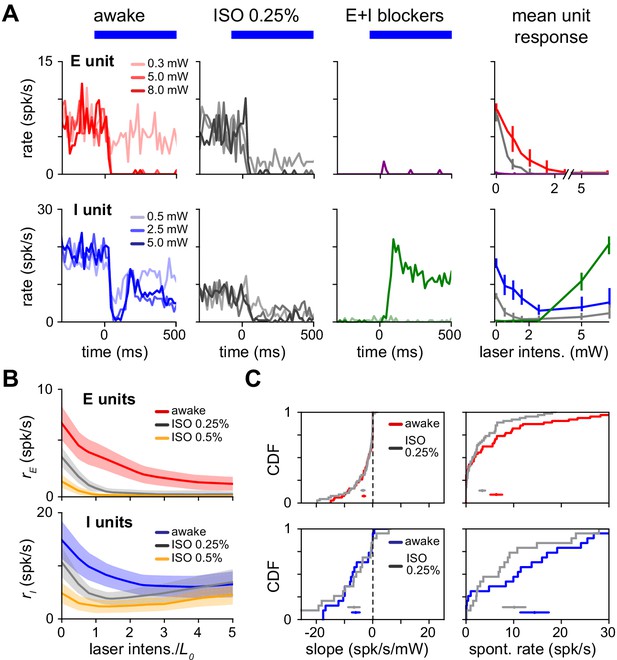
Paradoxical response is preserved with lower network activity due to anesthesia.
(A) Single excitatory (top) and inhibitory (bottom) unit response in the awake state (no anesthesia, no synaptic blockers), under anesthesia with no blockers (isoflurane, 0.25%) and with synaptic blockers (CNQX, APV, bicuculline; Materials and methods) plus anesthesia. (B) Population average response with (gray) and without (blue;red) anesthesia. Spontaneous firing rates are reduced for both the E (top) and I (bottom) populations below the awake firing rates, yet inhibitory paradoxical suppression is preserved with anesthesia (lower panel: gray line shows negative initial slope). In these experiments, inhibitory responses are weaker at high powers, but this does not affect paradoxical suppression. (C) Distribution of initial slope and spontaneous rate before and after anesthesia. Initial slope is largely preserved while excitatory and inhibitory spontaneous rates are suppressed. Colored horizontal bars within each panel show mean ± SEM for each distribution. Initial slopes are plotted here non-normalized (units spk/s/mW) to show the slopes are quantitatively similar across firing rate changes; normalized slopes are shown in Figure 8—figure supplement 1, and their means and medians remain negative across anesthesia state.
Figure 8—figure supplement 1
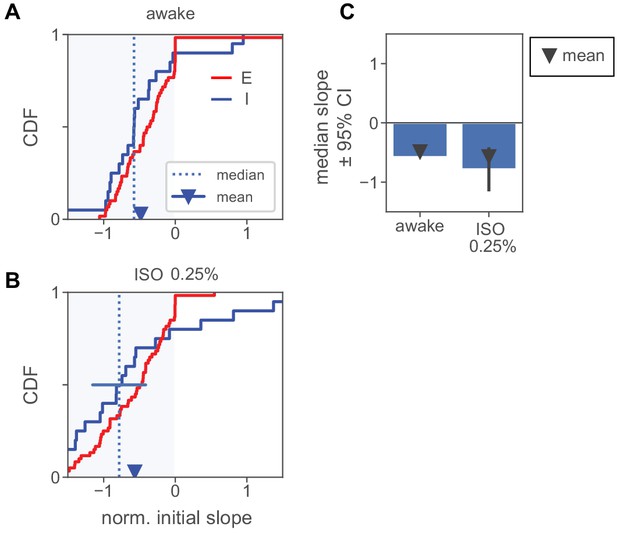
Normalized initial slopes for units recorded in anesthesia experiments.
(A) Normalized slopes for E and I units in awake recordings. Conventions as in Figure 5D. (B) Normalized slopes for E and I units in recordings with 0.25% isoflurane. More inhibitory units have a positive initial slope than in (A), but the mean and median remain negative. This increase in heterogeneity may be due to the network moving closer to an ISN transition point as firing rates are decreased by anesthesia. (C) Summary of mean and median slopes for inhibitory units. Both mean and median are significantly negative in both cases. (Mean, awake: , iso: , via t-test; median, awake: , iso: , Mann-Whitney U test) Solid black bars: 95% confidence interval for median via bootstrap.
Appendix 1—figure 1
Network dynamics with short term depression.
(A) Excitatory (red) and inhibitory (blue) nullclines of Equation A7. Different columns correspond to different values of (from left to right, , 3.42, 0.60); symbols correspond to the stationary solutions of the Equation A7. STD bends the excitatory nullcline downward, with a decrease that starts when . Since increasing moves the inhibitory nullcline to the left, paradoxical inhibitory response emerges only if the nullclines meet in the region of positive slope of the excitatory nullcline. (B) As in (A) but for Excitatory (red) and x (black) nullclines of Equation A7. Dashed lines correspond to threshold for paradoxical response (purple, Equation A9) and stability of the excitatory population with fixed and (green, Equation A12). Note that paradoxical response can appear only if the network with fixed is unstable. Therefore, if a network is stabilized by STD, it cannot show paradoxical response. (C) Dynamics of excitatory neurons in response to perturbations applied at time . Different colors correspond to different constraints on the dynamics. Different columns are as in panels A and B. (D) Values of as a function of for which the network: has paradoxical response (Equation A9, purple), is stable with fixed (Equation A12, green), is stable with fixed and (Equation A11, red). Paradoxical inhibitory response emerges only if the excitatory subnetwork is unstable on its own () and with STD and fixed inhibition (Equation A12). Symbols correspond to the stationary solutions of panels A and B. Simulation parameters are: , , , , , , , , , , = 500 ms, = 0.6.
Appendix 2—figure 1
Population response in the three phases of the experiment.
(A) Optimal fit of population response given by Equation B1. (B) Distributions (lines) and medians (arrows) of inferred parameters obtained with data bootstrap; dashed lines are optimal parameters reported in the text. (C) Distribution (line) and median (arrow) of self excitation of excitatory cells computed from data using Equation B6. The inferred values are distributed above the instability point (red line). (D) Distributions (lines) and medians (arrows) of recurrent excitation (, purple), recurrent inhibition (, blue), feed-forward+recurrent excitation (, red), and total input (, gray) to excitatory cells. As discussed in the text, inputs are of order threshold (dashed line); data are consistent with fluctuation driven firing (Amit and Brunel, 1997; van Vreeswijk and Sompolinsky, 1996; van Vreeswijk and Sompolinsky, 1998) and loose balance regime (Ahmadian and Miller, 2019).
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Inhibition stabilization is a widespread property of cortical networks
eLife 9:e54875.
https://doi.org/10.7554/eLife.54875
