Lapses in perceptual decisions reflect exploration
- Cold Spring Harbor Laboratory, Cold Spring Harbor, United States
- CSHL School of Biological Sciences, Cold Spring Harbor, United States
- University of California, Los Angeles, United States
Figures
Figure 1
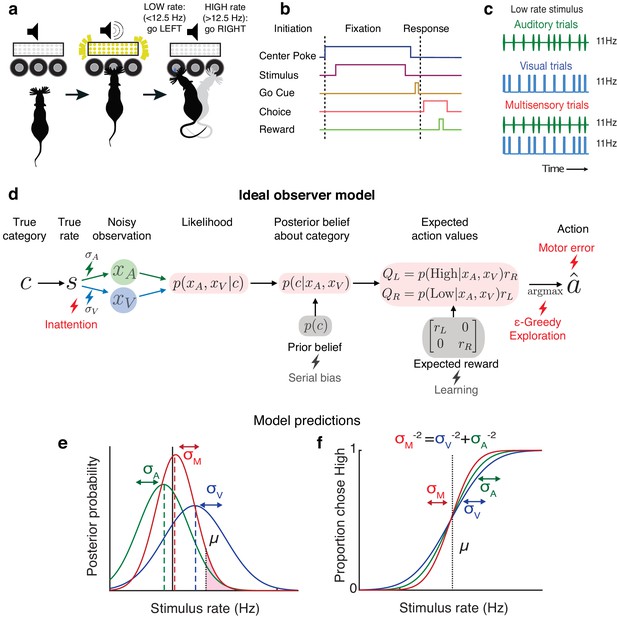
Testing ideal observer predictions in perceptual decision-making.
(a) Schematic drawing of rate discrimination task. Rats initiate trials by poking into a center port. Trials consist of visual stimuli presented via a panel of diffused LEDs, auditory stimuli presented via a centrally positioned speaker, or multisensory stimuli presented from both. Rats are rewarded with a 24 μL drop of water for reporting high-rate stimuli (greater than 12.5 Hz) with rightward choices and low-rate stimuli (lower than 12.5 Hz) with leftward choices. (b) Timeline of task events. (c) Example stimulus on auditory (top), visual (middle), and multisensory trials (bottom). Stimuli consist of a stream of events separated by long (100 ms) or short (50 ms) intervals. Multisensory stimuli consist of visual and auditory streams carrying the same underlying rate. Visual, auditory, and multisensory trials were randomly interleaved (40% visual, 40% auditory, and 20% multisensory). (d) Schematic outlining the computations of a Bayesian ideal observer. Stimulus belonging to a true category c with a true underlying rate s gives rise to noisy observations and , which are then integrated with each other and with prior beliefs to form a multisensory posterior belief about the category, and further combined with reward information to form expected action values . The ideal observer selects the action with maximum expected value. Lightning bolts denote proposed sources of noise that can give rise to (red) or exacerbate (gray) lapses, causing deviations from the ideal observer. (e) Posterior beliefs on an example trial assuming flat priors. Solid black line denotes true rate, and blue and green dotted lines denote noisy visual and auditory observations, with corresponding unisensory posteriors shown in solid blue and green. Solid red denotes the multisensory posterior, centered around the maximum a posteriori rate estimate in dotted red. Shaded fraction denotes the probability of the correct choice being rightward, with μ denoting the category boundary. (f) Ideal observer predictions for the psychometric curve, that is, proportion of high-rate choices for each rate. Inverse slopes of the curves in each condition are reflective of the posterior widths on those conditions, assuming flat priors. The value on the abscissa corresponding to the curve’s midpoint indicates the subjective category boundary, assuming equal rewards and flat priors.
Figure 2
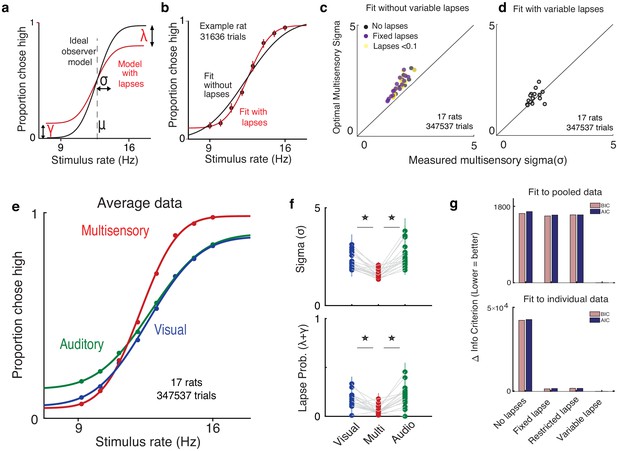
Deviations from ideal observer reflect lapses in judgment.
(a) Schematic psychometric performance of an ideal observer (black) vs. a model that includes lapses (red). The ideal observer model includes two parameters: midpoint (μ) and inverse slope (σ). The four-parameter model includes μ, σ, and lapse probabilities for low-rate (γ) and high-rate choices (λ). Dotted line shows the true category boundary (12.5 Hz). (b) Subject data was fit with a two-parameter model without lapses (black) and a four-parameter model with lapses (red). (c and d) Ideal observer predictions vs. measured multisensory sigma for fits with and without variable lapses across conditions. (c) Multisensory integration seems supra-optimal if lapses are not accounted for (no lapses, black), fixed across conditions (fixed lapses, purple), or assumed to be less than 0.1 (restricted lapses, yellow). (d) Optimal multisensory integration is restored when allowing lapses to vary freely across conditions (n = 17 rats. Points represent individual rats. Data points that lie on the unity line represent cases in which the measured sigma was equal to the optimal prediction). (e) Rats’ psychometric curves on auditory (green), visual (blue), and multisensory (red) trials. Points represent data pooled across 17 rats, and lines represent separate four-parameter fits to each condition. (f) Fit values of sigma (top) and lapse parameters (bottom) on unisensory and multisensory conditions. Both parameters showed significant reduction on the multisensory conditions (paired t-test, p<0.05); n = 17 rats (347,537 trials). (g) Model comparison using Bayes Information Criterion (pink) and Akaike Information Criterion (blue) for fits to pooled data across subjects (top) and to individual subject data (bottom). Lower scores indicate better fits. Both metrics favor a model where lapses are allowed to vary freely across conditions (‘Variable lapse’) over one without lapses (‘No lapses’), one with a fixed probability of lapses (‘Fixed lapse’), or where the lapses are restricted to being less than 0.1 (‘Restricted lapse’).
Figure 3 with 3 supplements
Uncertainty-guided exploration offers a novel explanation for lapses.
Models of lapses in decision-making: (a) Inattention model of lapses. Left panel: Observer’s posterior belief about rate. On a large fraction of trials given by , the observer attends to the stimulus and has a peaked belief about the rate whose width reflects perceptual uncertainty (red curve on matched trials, orange curve on neutral trials), but on a small fraction of trials given by , the observer does not attend to the stimulus (black curve), leading to equal posterior beliefs of rates being high or low (shaded, clear regions of curves respectively) and guesses according to the probability , giving rise to lapses (right panel). The sum of lapse rates then reflects , while their ratio reflects the . Since matched and neutral trials are equally salient, they are expected to have the same and hence similar overall lapse rates. (b) Fixed error model of lapses. Lapses could arise due to motor errors occurring on ε fraction of trials, or from decision rules that explore on a fixed proportion ε of trials (black), rather than always maximizing reward (blue). The sum of lapses reflects ε while their ratio reflects any in motor errors or exploration, leading to a fixed rate of lapses across conditions. (c) Uncertainty-guided exploration model. Lapses can also arise from more sophisticated exploratory decision rules such as the ‘softmax’ decision rule. Since the difference in expected value from right and left actions () is bounded by the maximum reward magnitudes and , even when the stimulus is very easy, the maximum probability of choosing the higher value option is not 1, giving rise to lapses. Lapse rates on either side are then proportional to the reward magnitude on that side, and to a ‘temperature’ parameter β that is modulated by the uncertainty in action values. Conditions with higher overall perceptual uncertainty (e.g. neutral, orange) are expected to have higher value uncertainty, and hence higher lapses. (d) Left: multisensory stimuli designed to distinguish between attentional and non-attentional sources of lapses. Standard multisensory stimuli with matched visual and auditory rates (top) and ‘neutral’ stimuli where one modality has a rate very close to the category boundary and is uninformative (bottom). Both stimuli are multisensory and designed to have equal bottom-up salience, and can only be distinguished by attending to them and accumulating evidence. Right: rat performance on interleaved matched (red) and neutral (orange) trials. (e) Model fits (solid lines) overlaid on average data points. Deviations from model fits are denoted with arrows. The exploration model (bottom) provides a better fit than the inattention model (top), since it predicts higher lapse rates on neutral trials (orange). (f) Model comparison using Bayes Information Criterion (pink) and Akaike Information Criterion (blue) both favor the uncertainty-guided exploration model for pooled data (top) as well as individual subject data (bottom).
Figure 3—figure supplement 1
Uncertainty-dependent exploration is the only model that accounts for behavioral data from all three manipulations.
Columns: data/predictions for three experimental manipulations. Left: unisensory (blue, green) vs. multisensory (red). Middle: matched (red) vs. neutral (orange) multisensory. Right: increased (green) or decreased (red) rightward reward vs. equal reward (black) on auditory trials. (a–d): Four candidate models. (a) Ideal observer model predicts no lapses and only changes in sensitivity/bias across conditions. (b) Fixed motor error model predicts a constant rate of lapses across conditions in addition to changes in sensitivity/bias predicted from the ideal observer. (c) Inattention model predicts that the overall lapse rate (sum of lapses on both sides) depends on the level of bottom-up attentional salience, allowing for different rates for unisensory and multisensory trials. It also predicts that the lapse rate on neutral trials should be equal to that on multisensory trials, and that manipulating rightward reward should affect both lapse rates. (d) Uncertainty-dependent exploration model predicts that overall lapse rate depends on the level of exploratoriness and hence uncertainty associated with that condition, allowing for different lapse rates on unisensory and multisensory trials. It also predicts that the lapse rate on neutral trials should be equal to that on auditory trials and manipulating rightward reward should only affect high-rate lapses. (e) Data from an example rat on all three manipulations.
Figure 3—figure supplement 2
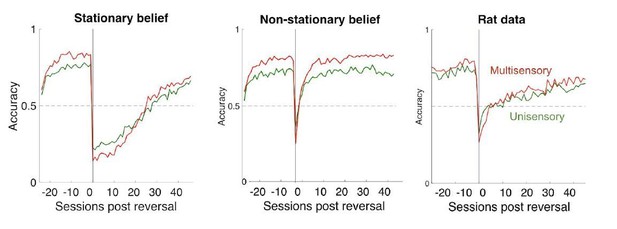
Thompson sampling, which balances exploration and exploitation, predicts lapses that increase with perceptual noise.
(a) Formulation of perceptual decision-making task as a partially observable contextual bandit. To solve this task, an observer needs to infer the true category of the stimulus (Low or High) based on noisy observations, and pick the best action given the inferred category (Left for Low, Right for High). This requires accurately learning the expected rewards from all four state-action pairs. (b) Schematic illustrating the explore–exploit tradeoff: Leftward state-action value beliefs i.e. expected reward from leftward actions (L) performed in different states (Hi, Lo) showing different levels of uncertainty depending on policy. Beliefs are updated based on outcomes using a Bayesian update rule that takes into account uncertainty in state estimation. A greedy policy (top left) that always picks the best action maximizes reward and learns well about the preferred state-action pairs (i.e. Lo-L) but has high uncertainty about the non-preferred pairs (Hi–L). A random policy (top right) earns reward at chance, but learns equally well about all state-action pairs. An ε-greedy policy (bottom left) learns well about the non-preferred pair, but leaves the choice of ε unspecified, and continues exploring even after it has learnt the values well, continuing to forego rewards. Thompson sampling (bottom right) tunes the amount of exploration to the current uncertainties in each value, and balances immediately reward-maximizing decisions with decisions that reduce uncertainty, maximizing average reward in the long term. (c) Cumulative regret, i.e. foregone reward accrued by different policies on the rate discrimination task as a function of training, with lower regret being more desirable. Black – random exploration, Pink – greedy, Purple – ε-greedy, and Yellow – Thompson sampling. Thompson sampling outperforms all other policies by achieving the minimum regret. (d) Learnt beliefs about expected reward with Thompson sampling at various levels of perceptual uncertainty. Low levels of sensory noise (left top) produce more separable beliefs, while higher levels of sensory noise (left bottom) lead to large perceptual uncertainty, yielding highly overlapping belief distributions owing to a reduced ability to assign obtained rewards to one of the states. (Right) Simulated performance averaged across 2000 trials of the Bayesian observer, under a Thompson sampling policy. The observer makes fewer exploratory choices for lower levels of sensory noise (orange) owing to the more separable value beliefs, giving rise to lower lapse rates. (e) Session-averaged lapse rates as a function of sensory noise in simulations (left, center) and multisensory rat data (right). Simulations were done under increasing levels of sensory noise (colors going from hot to cold) under beliefs that action values are stationary (left) or non-stationary (center), solid lines indicate linear best-fit. Individual rat data was fit with a constrained version of the exploration model where total lapse rate was constrained to be linearly related to sensory noise across all modality conditions (auditory – green, multisensory – red, and visual – blue). Lines indicate best fit linear constraints for each rat. (f) Learnt beliefs about expected reward with Thompson sampling during early (left top) and late (left bottom) stages of training. Training reduces uncertainty about expected rewards, producing more separable beliefs and yielding less exploration and lower lapse rates over time (right – simulated average performance). (g) Session-wise lapse rates in simulated (left, center) and rat data (right) as a function of both training and sensory noise. Simulations show decreasing lapse rates over training that asymptote at zero under stationary beliefs (left) and to nonzero values dictated by sensory noise under non-stationary beliefs (center). Rat data was separated by session starting from the earliest day of training with all three modalities, and combined across rats to produce session-wise fits, and the resulting lapse rates were fit with an exponential curve for each modality (solid lines indicate best-fit curves for multisensory – red, visual – blue, and auditory – green).
Figure 3—figure supplement 3
Uncertainty guided exploration outperforms competing models for average and individual data.
(a) Fits of the four models (ideal observer, fixed motor error, inattention, and exploration) to average rat data on unisensory (blue – visual, green – auditory) and multisensory (red) trials. (b) Exploration model fits to unisensory and multisensory data for 17 individual animals. (c) Model comparison for individual animals using Bayes Information Criterion (BIC; left), Akaike Information Criterion (AIC; right) of the four aforementioned models, plus a constrained version of the exploration model corresponding to Thompson sampling. Darker colors are lower BICs/AICs, denoting a better fit. (d) Summed model comparison metrics across animals, showing that inattention and exploration models fit the data equally well, and much better than the ideal observer or fixed error models. Thompson sampling is preferred by BIC, since it fits as well as exploration model but with fewer effective parameters. (e) Fits of the four models to average data including neutral trials (orange) provide a stronger test of the inattention model. (f) Exploration model fits to multisensory data including neutral trials for five individual animals. (g) Model comparison for individual animals. (h) Summed model comparison metrics across animals shows that the uncertainty-guided exploration model performs better than other models.
Figure 4 with 2 supplements
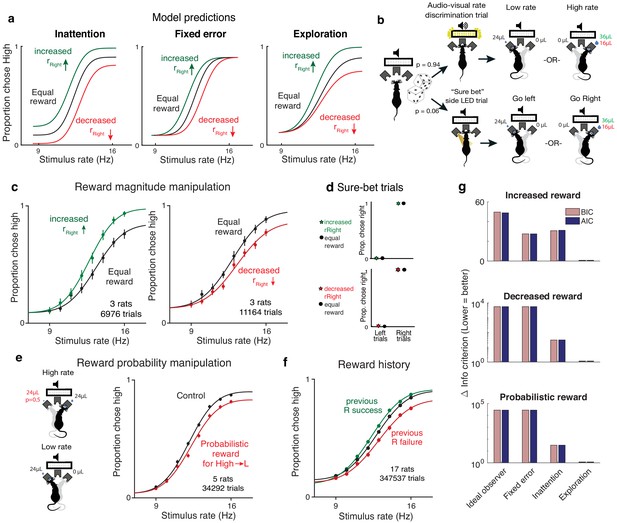
Reward manipulations match predictions of the exploration model.
(a) The inattention, fixed error, and exploration models make different predictions for increases and decreases in the reward magnitude for rightward (high-rate) actions. The inattention model (left panel) predicts changes in lapses for both high- and low-rate choices, while fixed error models such as motor error or ε-greedy (center) predict changes in neither lapse, and the uncertainty-dependent exploration model (right) predicts changes in lapses only for high-rate choices. Black line denotes equal rewards on both sides; green, increased rightward reward; red, decreased rightward reward. (b) Schematic of rate discrimination trials and interleaved ‘sure bet’ trials. The majority of the trials (94%) were rate discrimination trials as described in Figure 1. On sure-bet trials, a pure tone was played during a 0.2 s fixation period and one of the side ports was illuminated once the tone ended to indicate that reward was available there. Rate discrimination and sure-bet trials were randomly interleaved, as were left and right trials, and the rightward reward magnitude was either increased (36 μL) or decreased (16 μL) while maintaining the leftward reward at 24 μL. (c) Rats’ behavior on rate discrimination trials following reward magnitude manipulations. High-rate lapses decrease when water reward for high-rate choices is increased (left panel; n = 3 rats, 6976 trials), while high-rate lapses increase when reward on that side is decreased (right panel; n = 3 rats, 11,164 trials). Solid curves are exploration model fits with a single parameter change accounting for the manipulation. (d) Rats show nearly perfect performance on sure-bet trials and are unaffected by reward manipulations on these trials. (e) Reward probability manipulation. (Left) Schematic of probabilistic reward trials, incorrect (leftward) choices on high rates were rewarded with a probability of 0.5, and all other rewards were left unchanged. (Right) Rats’ behavior and exploration model fits showing a selective increase in high-rate lapses (n = 5 rats, 34,292 trials). (f) Rats’ behavior on equal reward trials conditioned on successes (green) or failures (red) on the right on the previous trials resembles effects of reward size manipulations. (g) Model comparison showing that Akaike Information Criterion and Bayes Information Criterion both favor the exploration model on data from all three manipulations.
-
Figure 4—source data 1
Fit parameters to pooled data across rats.
- https://cdn.elifesciences.org/articles/55490/elife-55490-fig4-data1-v2.xlsx
Figure 4—figure supplement 1
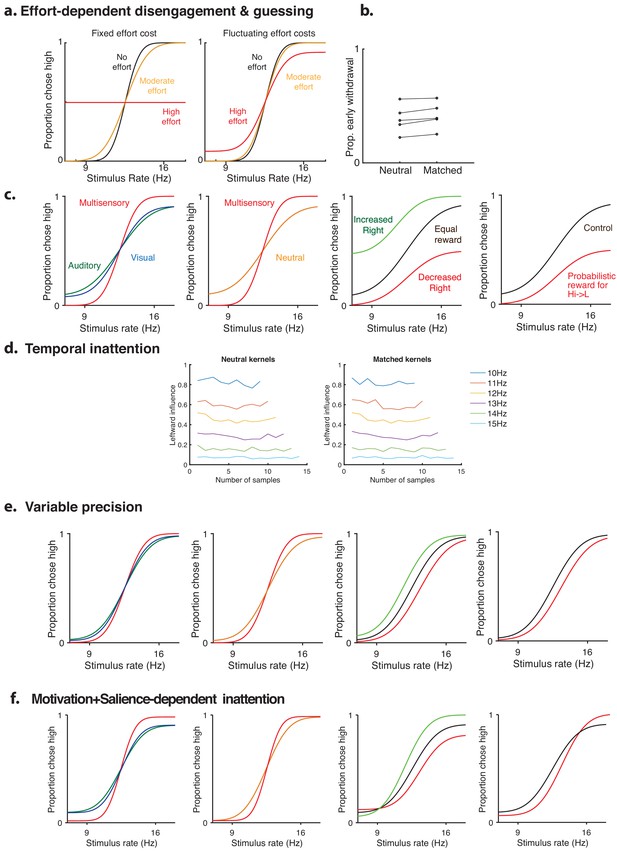
Alternative models of inattentional lapses.
Predictions of alternative models of lapses. (a) Effort-dependent disengagement model: In this model, there is an additional cost or mental effort to being engaged in the task which could vary with condition, and an additional random guessing action. If the net payoff of engagement is not greater than the average value of a guess, then it guesses randomly. Such a model does not produce lapses if the effort is fixed across trials (left), but could produce lapses if the effort fluctuates from trial to trial (center). (b) Proportion of trials on which the animal withdrew prematurely does not vary between matched and neutral trials, suggesting that rats are not disengaging preferentially on neutral trials. (c) Predictions of the effort-dependent disengagement model. The model accurately predicts increased lapses on unisensory trials (left panel, green/blue traces) and neutral multisensory trials (middle left panel, orange trace). However, for asymmetric reward manipulations (middle right – reward magnitude, right – reward probability), the model fails to predict our behavioral observation (Figure 4d) that only lapses on the manipulated side are affected. (d) Temporal inattention model: in this model, temporal weighting of evidence differs between matched and neutral trials. To test this, we compared psychophysical kernels on matched and neutral trials. The temporal dynamics of attention are unchanged between the two kinds of trials, arguing against the temporal inattention model. (e) Variable precision model: in this model, the sensory noise (or its inverse, precision) fluctuates from trial to trial, producing heavy tailed performance curves with apparent 'lapses’. The model accurately predicts increased apparent lapses on unisensory trials (left panel, green/blue traces) and neutral multisensory trials (middle left panel, orange trace). However, for asymmetric reward manipulations (middle right, right), the model fails to predict our behavioral observation (Figure 4d) that lapses only on the manipulated side are affected. Like other models of inattention, it predicts that manipulating reward on one side should affect both lapses. (f) Motivation + salience-dependent inattention: in this model, inattention is determined not just by salience, but also motivation, which in turn depends on average reward. This model’s predictions on unisensory, multisensory (left) and neutral (middle left) trials are identical to the inattention model, but on asymmetric reward manipulations, it predicts that total lapse rate should change as a function of total reward. As a result, when reward magnitude on one side is increased or decreased (middle right), total lapse rate also increases or decreases, in addition to the vertical shifts predicted by inattention. However, on the reward probability manipulation (right), it predicts a *decrease* in total lapse rate owing to the overall higher average reward, in addition to a downward shift predicted by inattention, unlike the rat data (Figure 4e) where overall lapse rate *increases* as a consequence of high-rate lapses selectively *increasing*.
Figure 4—figure supplement 2
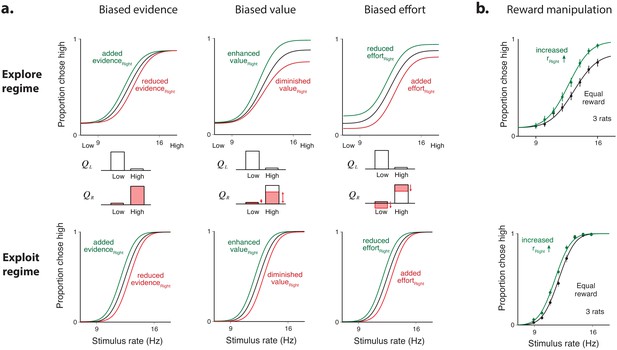
Psychometric functions with lapses make it possible to assign perturbations effects to specific stages of decision-making.
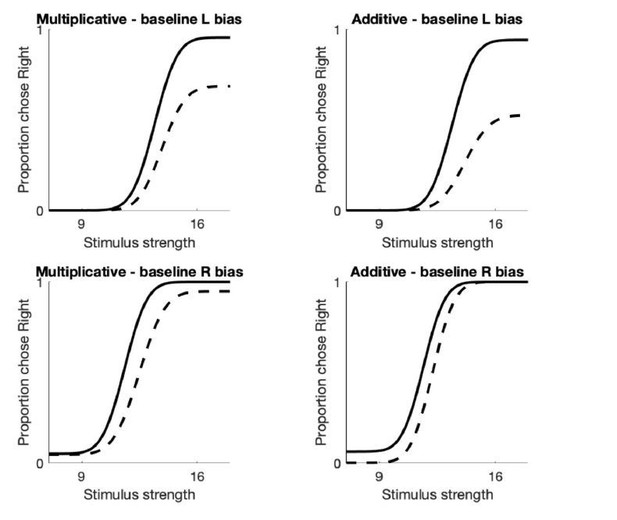
(a) (Top row) Model predictions for biased sensory evidence (left), enhanced rightward action value (center), and reduced effort in performing rightward movements (right) in an exploratory regime where lapses are sizeable. The three kinds of perturbations affect decisions at the sensory, value, or motor stages and predict different effects on lapses. (Middle row) Effects of the three manipulations on the four stimulus-action value pairs. Biasing rightward evidence (left) leaves stimulus-action value pairs unchanged, while biasing the learnt rightward values (center) selectively affects rightward action values on high rates and biasing rightward effort (right) affects both high- and low-rate action values equally. (Bottom row) All three perturbations reduce to the same effect (horizontal shift) in the absence of lapses, that is, in the exploit regime. (b) Example data from two rats that experienced the same perturbation: increased rewards on the right port. The rats differ in the extent to which their psychometric functions have lapses. Top: In a psychometric function with lapses, the perturbation (green trace) leads to an interpretable change: the asymmetric change in lapses is only consistent with the explanation that the perturbation enhanced the value of rightward choices (as in [a], top, middle). The perturbation did not drive a change consistent with biased evidence or biased effort. Bottom: In a psychometric function with negligible lapses, the perturbation (red trials) lead to a cryptic change in the psychometric function: the observed shift could equivalently have been driven by biased evidence, value, or effort (as in [a], bottom three panels). Therefore, although the perturbation likely caused the same change in the two rats, an experimenter is only able to accurately explain this change in a rat with lapses.
Figure 5 with 7 supplements
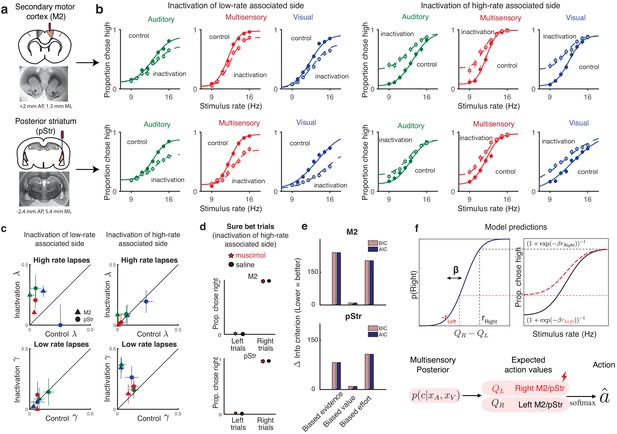
Inactivation of secondary motor cortex and posterior striatum affects lapses, suggesting a role in action value encoding.
(a) Schematic of cannulae implants in M2 (top) and pStr (bottom) and representative coronal slices. For illustration purposes only, the schematic shows implants in the right hemisphere; however, the inactivations shown in panel (b) were performed unilaterally on both hemispheres. (b) Unilateral inactivation of M2 (top) and pStr (bottom). Left six plots: inactivation of the side associated with low rates shows increased lapses for high rates on visual (blue), auditory (green), and multisensory (red) trials (M2: n = 5 rats; 10,329 control trials, full line; 6174 inactivation trials, dotted line; pStr: n = 5 rats; 10,419 control trials; 6079 inactivation trials). Right six plots: inactivation of the side associated with high rates shows increased lapses for low rates on visual, auditory, and multisensory trials (M2: n = 3 rats; 5678 control trials; 3816 inactivation trials; pStr: n = 6 rats; 11,333 control trials; 6838 inactivation trials). Solid lines are exploration model fits, accounting for inactivation effects across all three modalities by scaling all contralateral values by a single parameter. (c) Increased high-rate lapses following unilateral inactivation of the side associated with low rates (top left); no change in low-rate lapses (bottom left) and vice versa for inactivation of the side associated with high rates (top, bottom right). Control data on the abscissa is plotted against inactivation data on the ordinate. Same animals as in b. Green, auditory trials; blue, visual trials; red, multisensory trials. Abbreviations: posterior striatum (pStr), secondary motor cortex (M2). (d) Sure bet trials are unaffected following inactivation. Pooled data shows that rats that were inactivated on the side associated with high rates make near perfect rightward and leftward choices Top, M2 (three rats); bottom, pStr (six rats). (e) Model comparison of three possible multisensory deficits – reduction of contralateral evidence by a fixed amount (left), reduction of contralateral value by a fixed amount (center), or an increased contralateral effort by a fixed amount (right). Both Akaike Information Criterion and Bayes Information Criterion suggest a value deficit. (f) Proposed computational role of M2 and striatum. Lateralized encoding of left and right action values by right and left M2/pStr (bottom) explains the asymmetric effect of unilateral inactivations on lapses (top).
Figure 5—figure supplement 1
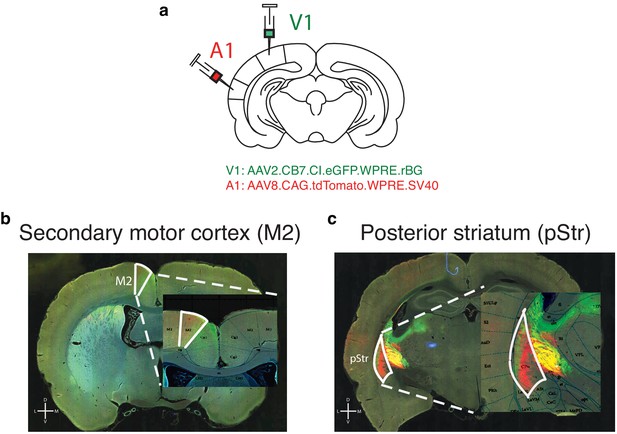
pStr and M2 receive direct projections from visual and auditory cortex.
(a) Schematic of tracing experiments. AAV2.CB7.CI.EGFP.WPRE.RBG and AAV2.CAG.tdTomato.WPRE.SV40 constructs were injected unilaterally to primary visual (V1) and auditory (A1) cortices, respectively (V1 coordinates: 6.9 mm posterior to Bregma; 4.2 mm to the right of midline; A1 coordinates: 4.7 mm posterior to Bregma; 7 mm to the right of midline). (b) Secondary motor cortex (M2) receives inputs from V1 and A1 as shown by green and red fluorescence. (c) Posterior striatum (pStr) receives direct inputs from V1 and A1 as shown by green and red fluorescence. Yellow signal medial to pStr reflects overlapping passing fibers.
Figure 5—figure supplement 2
Histological slices of implanted rats.
Representative coronal slices of all rats implanted with cannulae for muscimol inactivation experiments. (a) Six rats were bilaterally implanted in posterior striatum (pStr). (b) Five rats were implanted in secondary motor cortex (M2).
Figure 5—figure supplement 3
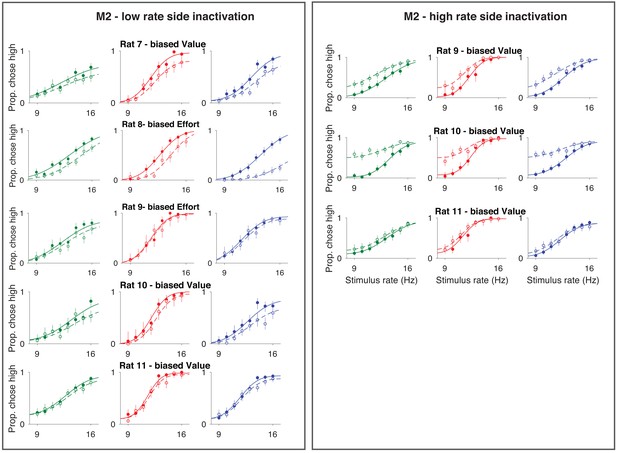
Single rat performance following M2 inactivation.
Left: inactivation of the low-rate associated side. Rat shows increased lapses on high-rate trials on all sensory modalities. Right: inactivation of the high-rate associated side. Rat shows increased lapses on low-rate trials on all sensory modalities. Auditory (green), visual (blue), and multisensory (red).
Figure 5—figure supplement 4
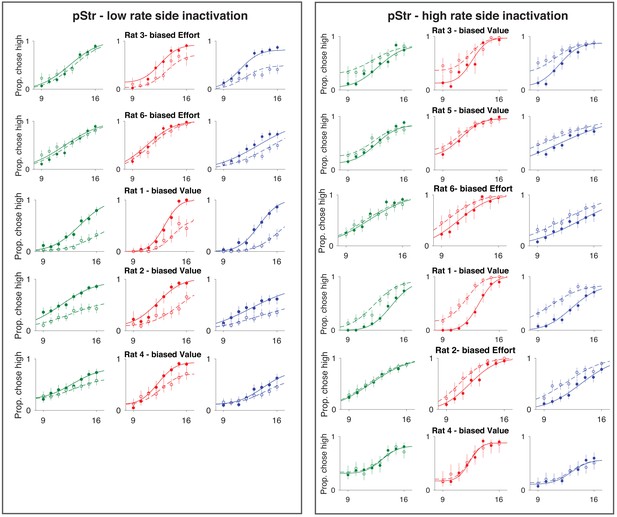
Single rat performance following pStr inactivation.
Left: inactivation of the low-rate associated side. Rat shows increased lapses on high-rate trials on all sensory modalities. Right: inactivation of the high-rate associated side. Rat shows increased lapses on low-rate trials on all sensory modalities. Auditory (green), visual (blue), and multisensory (red).
Figure 5—figure supplement 5
Unilateral inactivation of M2 or pStr biases performance ipsilaterally and increases contralateral lapses.
Performance of the same rats shown in Figure 5b depicted as a function of the inactivated side (right or left) and the rate-contingency in which they were trained (standard or reverse), along with fits from the biased value model (solid lines – saline, dotted lines - muscimol). Standard contingency: high rate = go right, low rate = go left; reverse contingency: high rate = go left, low rate = go right. Each quadrant shows four plots: three psychometrics for rate discrimination trials and one for performance on sure-bet trials. auditory (green), visual (blue), and multisensory (red). (a–d) M2 inactivation. (e–h) pStr inactivation. (a), (d) Rats trained on the standard contingency and inactivated on the left hemisphere show increased lapses on the high rates (i.e., fewer rightward choices on high rates). No effect on sure-bet trials. (b), (f) Rats trained on the standard contingency and inactivated on the right hemisphere show increased lapses on the low rates (i.e., fewer leftward choices on low rates). No effect on sure-bet trials. (c), (g) Rats trained on the reverse contingency and inactivated on the left hemisphere show increased lapses on the low rates (i.e., fewer rightward choices on low rates). No effect on sure-bet trials. No data for this condition for M2 inactivation. (d), (h) Rats trained on the reverse contingency and inactivated on the right hemisphere show increased lapses on the high rates (i.e., fewer leftward choices on high rates). No effect on sure-bet trials for pStr inactivated animals; no data for M2 inactivated animals.
Figure 5—figure supplement 6
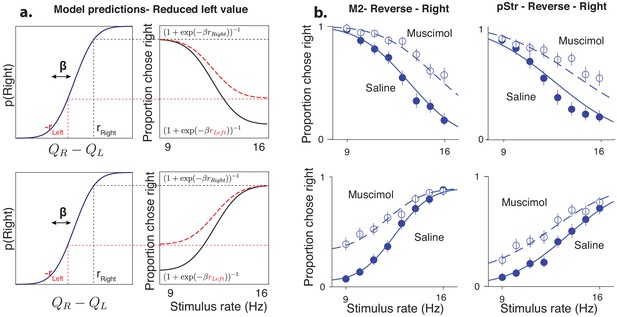
Inactivations devalue contralateral actions irrespective of associated stimulus.
(a) Model predictions for rightward inactivations on standard (top) and reversed (bottom) stimulus-response contingencies – in both cases, the model predicts that reduced leftward action values should only affect lapses on the side associated with leftward movements. (b) Inactivation data on visual trials from M2 (left) or pStr (right) along with fits from the biased value model (solid lines – saline, dotted lines – muscimol) shows a pattern of effects consistent with action value deficits, irrespective of the contingency.
Figure 5—figure supplement 7
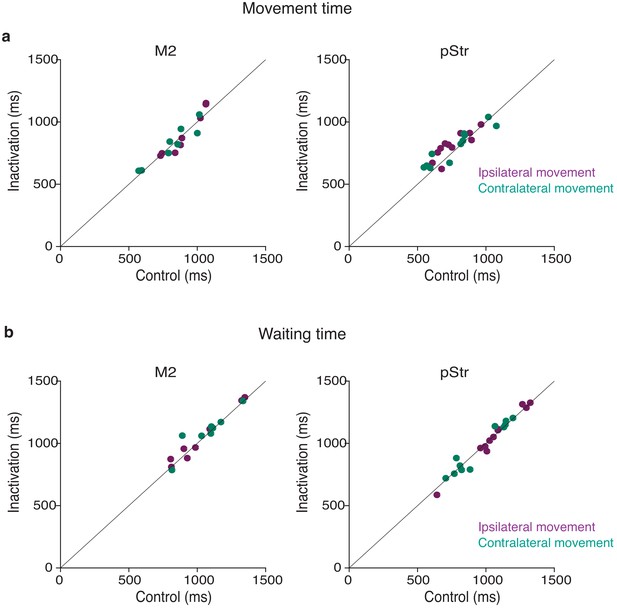
No significant effect on movement parameters following muscimol inactivation.
(a) Mean movement times from the center port to the side ports were not significantly different following muscimol inactivation of M2 (left; p=0.9554 for contralateral, 0.9852 for ipsilateral movements; n = 5 rats) or pStr (right; p=0.6629 for contra, p=0.2615 for ipsi, n = 6 rats). Control data on the abscissa is plotted against inactivation data on the ordinate. Purple, movement toward the side ipsilateral to the inactivation site; blue, movement toward the side contralateral to the inactivation site; error bars (s.e.m.) are not visible because they were obscured by the markers in all cases. (b) Mean wait times in the center port were not significantly different following muscimol inactivation of M2 (left; p=0.7612 for contra, p=0.8896 for ipsi, n = 5 rats) or pStr (right; p=0.9128 for contra, p=0.9412 for ipsi, n = 6 rats). All p-values were computed from paired t-tests. Error bars (s.e.m.) are not visible because they were obscured by the markers in all cases.
Author response image 1
Author response image 2
Author response image 3
Author response image 4
Author response image 5
Author response image 6
Author response image 7
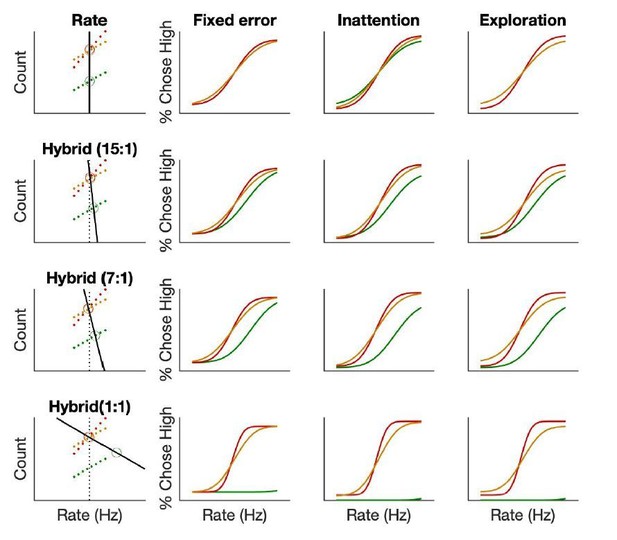
Use of count information generates bias in psychometric functions.
Simulations demonstrating the effect of 4 different linear decoders (1st column) on psychometric functions under the fixed error (2nd column), inattention (3rd column) and exploration (4th column) models. Dotted black lines indicate the true category boundary that separates “low” and “high” stimulus categories, solid black lines indicate the subjective category boundary for each decoder. Colored dots indicate stimulus sets in auditory (green), neutral (orange) and multisensory (red) conditions. Open circles indicate point of subjective equality i.e. stimulus that produces equal “high” and “low” evidence for each condition. Rate-only decoder (1st row) aligns with the true category boundary, producing unbiased psychometric functions across conditions, with models differing only in the total lapse rate of each condition. Hybrid decoders incorporating a small amount of count information (2nd row: 1/15th as much as rate, 3rd row: 1/5th as much as rate, 4th row: just as much as rate) that are unbiased on multisensory, neutral conditions produce a low-rate bias on auditory trials, with more use of count information producing higher bias. This produces horizontal shifts (i.e. bias) across models, and additionally produces vertical shifts (i.e. lapse bias) in inattention, exploration models, while preserving the predictions for total lapse rates across models/conditions.
Author response image 8
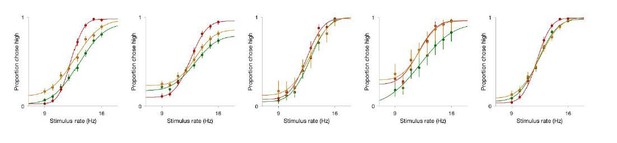
Bias in psychometric functions of individual rats.
Data from the 5 rats used in the neutral experiment, on auditory (green), neutral (orange) and multisensory (red) conditions, demonstrating individual variability in low-rate bias on auditory trials, compared to neutral/multisensory trials. Some rats (e.g. rightmost panel) show almost no bias, resembling the “rate-only” decoders, while others resemble “hybrid” decoders with weak influences fromcount information.
Author response image 9
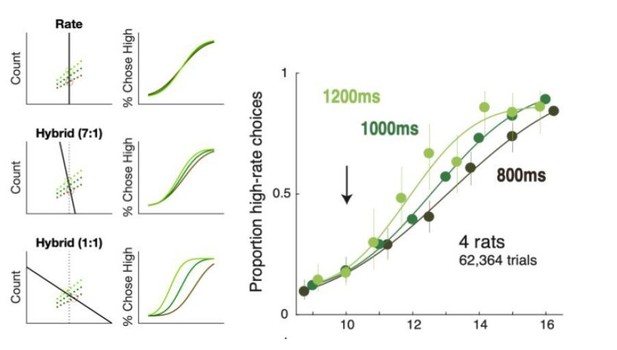
Duration manipulation on auditory trials confirms weak influence of count.
Data from 4 rats (right) shows that increasing (light green) or decreasing (brown) the duration of auditory trials produces slight high- or low-rate biases, resembling a hybrid decoder with a weak influence of count information(middle panel left).
Tables
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Strain, strain background (Rattus norvegicus domestica, male and female) | Long-Evans Rat | Taconic Farms | SimTac:LE | TAC: LONGEV-M, TAC: LONGEV-F |
| Recombinant DNA reagent | AAV2.CB7.CI.EGFP.WPRE.RBG | UPenn Vector Core | Obtained from the laboratory of Dr. Partha Mitra at CSHL | |
| Recombinant DNA reagent | AAV2.CAG.tdTomato.WPRE.SV40 | UPenn Vector Core | Obtained from the laboratory of Dr. Partha Mitra at CSHL | |
| Chemical compound, drug | Muscimol | abcam | ab120094 | |
| Software, algorithm | PALAMEDES toolbox | Prins and Kingdom, 2018 | doi: 10.3389/fpsyg.2018.01250 | |
| Software, algorithm | MATLAB | The Mathworks, Inc |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Lapses in perceptual decisions reflect exploration
eLife 10:e55490.
https://doi.org/10.7554/eLife.55490
