Distinct hierarchical alterations of intrinsic neural timescales account for different manifestations of psychosis
- Department of Psychiatry, Columbia University, United States
- New York State Psychiatric Institute, United States
- Department of Psychiatry, Yale University, United States
Figures
Figure 1 with 6 supplements
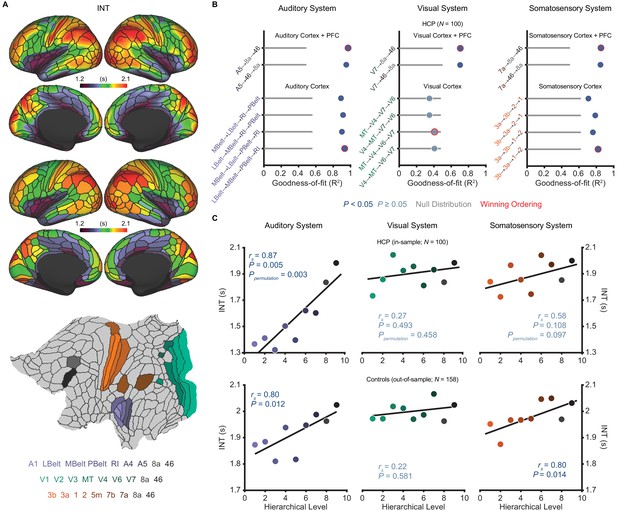
Model comparison to determine the hierarchical orderings of the auditory, visual, and somatosensory systems.
(A) Group-averaged intrinsic neural timescale (INT) map from the Human Connectome Project (HCP) dataset (N = 100; top), parcellated group-averaged INT map (middle), and flattened cortex showing the parcels in the auditory, visual, and somatosensory hierarchies (winning hierarchies underneath; bottom). Color coding of parcels indicates their anatomical and hierarchical location. (B) Goodness of fit (R2) of linear mixed-effects models predicting different hierarchical orderings of the auditory system (left), visual system (middle), and somatosensory system (right) from T1w/T2w and cortical thickness values in the HCP dataset (Materials and methods). First, the winning ordering (i.e. the model with the best goodness of fit) for each system was determined for the seven sensory cortex regions (bottom four models). Then, the winning ordering was determined for extended models with two downstream prefrontal cortex regions added to the respective winning models for the sensory cortex (top two models). Note that, for each of the four considered orderings within the sensory cortex for each system, only the four regions whose order is varied (out of 7 regions) are shown to delineate the models. For the auditory cortex, A1 was always the lowest order region while A4 and A5 were always the two highest order regions. For the visual cortex, V1, V2, and V3 were always the three lowest order regions. For the somatosensory cortex, 5m, 7b, and 7a were always the three highest order regions. Null distributions were generated by randomly permuting the hierarchical ordering across all regions in a given hierarchy (0th – 95th percentiles shown). (C) Scatterplots showing INT values plotted as a function of hierarchical level for the PFC-extended winning models in B (red outline) for the HCP dataset (top) and the healthy control group in the schizophrenia combined dataset (N = 158; bottom). LBelt, lateral belt; MBelt, medial belt; PBelt, parabelt; RI, retroinsular cortex; MT, middle temproal area.
-
Figure 1—source data 1
Data and code to reproduce Figure 1.
- https://cdn.elifesciences.org/articles/56151/elife-56151-fig1-data1-v1.zip
Figure 1—figure supplement 1
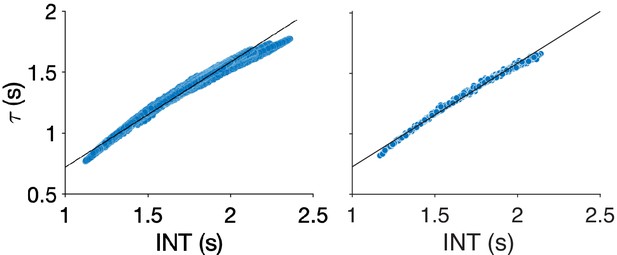
Comparison of different methods for neural timescale estimation: sum of initial positive period vs exponential fit.
Scatterplots showing the relationship between neural timescales estimated using the sum of the initial positive period (INT, x-axis) and an exponential fit (τ, y-axis) to the autocorrelation function. Results for vertices (left) and parcels (right). Lines of best-fit are shown for comparison. The INT method of Watanabe et al., 2019 is similar to estimating the decay rate of an exponential fit to the autocorrelation function (Murray et al., 2014). The former method was used in our study to maintain consistency with the previous study, which validated the technique against INT measured by electroencephalography (Watanabe et al., 2019). Additionally, this method avoids the need for nonlinear fitting—which is known to be challenging (Transtrum et al., 2010) and computationally expensive—and may be more robust. The difference between timescales estimated with the two methods was assessed in the 100 HCP subjects by comparing the group averaged timescale maps using Spearman correlation. The correlation between the two methods was almost perfect (vertices: rs = 0.9986, p<<0.01; parcels: rs = 0.9985, p<<0.01) but there is an upwards bias in values estimated using the method of Watanabe et al., 2019.
Figure 1—figure supplement 2
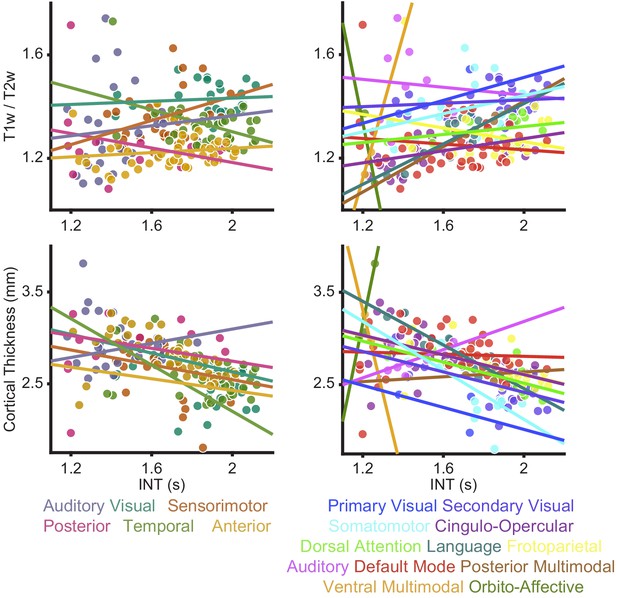
Relationships between intrinsic neural timescale and either T1w/T2w (myelin) or cortical thickness.
As reported in the Main Text, we did not observe a clear parcel-wide relationship between structural markers of hierarchy and intrinsic neural timescale (INT). These relationships were investigated using two parcel-groupings; those described by Glasser et al. (Glasser et al., 2016; left) and the Cole-Anticevic networks described by Ji et al. (Ji et al., 2019; right). To better characterize the relationship between myelin (top) or cortical thickness (bottom) and INT, intercepts for each parcel group (visual, auditory, sensorimotor, posterior, anterior, and temporal) or network (primary visual, secondary visual, somatomotor, cingulo-opercular, dorsal attention, language, frontoparietal, auditory, default mode, posterior multimodal, ventral multimodal, and orbito-affective) were introduced to allow for overall differences in INT-by-parcel-group (or INT-by-network) given the apparent differences observed in the data. Parcel-group-by-T1w/T2w-value (or network-by-T1w/T2w-value) interactions and parcel-group-by-cortical-thickness (or network-by-cortical-thickness) were also introduced to allow for differences in the relationship between T1w/T2w (or cortical thickness) and INT values across parcel groups (or networks). We found that an extended model with parcel-group intercepts and interactions of parcel-group-by-T1w/T2w explained significantly more variance in INT than the reduced model (no parcel-group intercepts or interactions): parcel groups differed in INT (model with parcel-group intercepts versus reduced model: F10,167 = 12.03, p<10−14) and their relationship between T1w/T2w and INT (model with parcel-group intercepts and interactions of parcel-group-by-T1w/T2w versus a model with parcel-group intercepts but no interaction terms: F5,167 = 5.55, p<10−4). Similar results were observed for the Cole-Anticevic Networks, where we found that an extended model with network intercepts and interactions of network-by-T1w/T2w explained significantly more variance in INT than the reduced model (no network intercepts or interactions): networks differed in INT (model with network intercepts versus reduced model: F22,155 = 4.62, p<10−8) and their relationship between T1w/T2w and INT (model with network intercepts and interactions of network-by-T1w/T2w versus model with network intercepts but no interactions: F11,155 = 2.15, p=0.020). For cortical thickness, we found that an extended model with parcel-group intercepts and interactions of parcel-group-by-cortical-thickness explained significantly more variance in INT than the reduced model (no parcel-group intercepts or interactions): parcel groups differed in INT (model with parcel-group intercepts versus reduced model: F10,167 = 8.59, p<10−10) and their relationship between cortical-thickness and INT (model with parcel-group intercepts and interactions of parcel-group-by-cortical-thickness versus a model with parcel-group intercepts but no interaction terms: F5,167 = 5.05, p<10−3). Similar results were observed for the Cole-Anticevic Networks, where we found that an extended model with network intercepts and interactions of network-by-cortical-thickness explained significantly more variance in INT than the reduced model (no network intercepts or interactions): networks differed in INT (model with network intercepts versus reduced model: F22,155 = 3.58, p<10−5) and their relationship between cortical-thickness and INT (model with network intercepts and interactions of network-by-cortical-thickness versus a model with network intercepts but no interactions: F11,155 = 1.96, p=0.036). These results suggest that the relationship between structural hierarchies (T1w/T2w and cortical thickness) and functional hierarchy (INT) is not constant across the whole brain but rather changes for different parcel groups and networks.
Figure 1—figure supplement 3
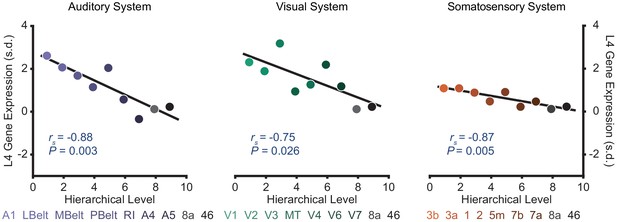
Selected sensory hierarchies demonstrate a hierarchical gradient of granular layer IV (L4) gene expression.
Scatter plots showing L4 gene expression plotted as a function of hierarchical level for the winning orderings. Expression is plotted in units of standard deviation (s.d.; σ) from the mean. Gene expression data are from the Allen Human Brain Atlas as compiled by Burt et al., 2018.
Figure 1—figure supplement 4
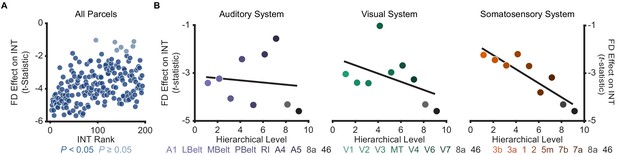
Effect of framewise displacement on estimated intrinsic neural timescales.
To determine the effect of head motion during resting-state fMRI data acquisition on estimated intrinsic neural timescale (INT) values, we used a linear-regression model to predict INT as a function of mean framewise displacement (FD) while controlling for age and gender. Because average FD represents a summary measure of head motion during the entire acquisition, this regression does not provide information regarding differential effects of sustained small levels of head motion versus infrequent but large levels of head motion. (A) t-statistic values from a regression model predicting INT from the average FD during fMRI data acquisition plotted as a function of the INT rank for 100 HCP subjects. Each datapoint represents one parcel. 181 out of 188 parcels showed significantly shorter INT with greater FD (Ppermutation = 0.01). (B) t-statistic values from parcels within the winning orderings of the auditory hierarchy (left), visual hierarchy (middle), and somatosensory hierarchy (right) plotted as a function of hierarchical level. No hierarchical-gradient effects of FD were observed.
Figure 1—figure supplement 5
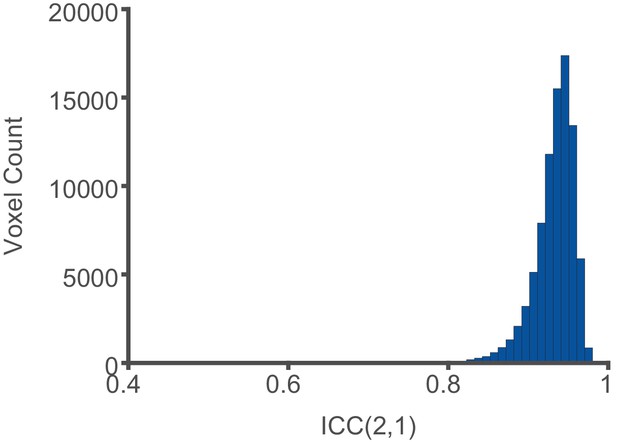
Reliability of intrinsic neural timescale estimation.
Intrinsic neural timescale (INT) maps for 100 HCP subjects were estimated in volume space and the values at each voxel falling within the 188 parcels of the HCP-MMP1.0 were compared when INT was estimated from the first 5 min or the last 5 min of fMRI acquisition. The INT maps showed excellent reliability based on the ICC(2,1) between the first and last 5 min of the fMRI acquisition (median ICC ±interquartile range across voxels: 0.94 ± 0.03).
Figure 1—figure supplement 6
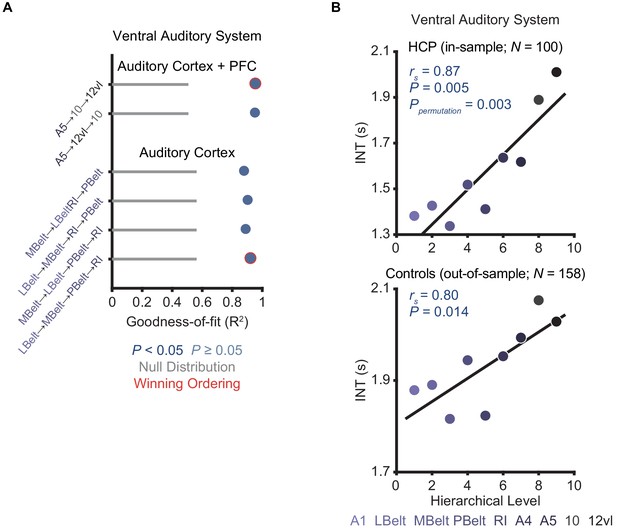
Model comparison to determine the hierarchical ordering of the ventral auditory pathway.
(A) Goodness of fit (R2) of linear mixed-effects models predicting different hierarchical orderings of the ventral auditory system from T1w/T2w and cortical thickness values in the HCP dataset (N = 100). First, the winning ordering (i.e. the model with the best goodness of fit) was determined for the seven auditory cortex regions (bottom four models); then, the winning ordering was determined for an extended model with two ventral downstream prefrontal cortex regions (areas 10 and 12vl) added to the winning model for the auditory cortex (top two models). Note that, for each of the four considered orderings within the auditory cortex, only the four regions whose order is varied (out of seven regions) are shown to denote the models. For the auditory cortex, A1 was always the lowest-order region while A4 and A5 were always the two highest-order regions. Null distributions were generated by randomly permuting the hierarchical ordering (0th – 95th percentiles shown). (B) Scatterplots showing intrinsic neural timescale (INT) values plotted as a function of hierarchical level for the PFC-extended winning model in B (red outline) for the HCP dataset (top) and the healthy control group in the schizophrenia combined dataset (N = 158; bottom).
Figure 2 with 2 supplements
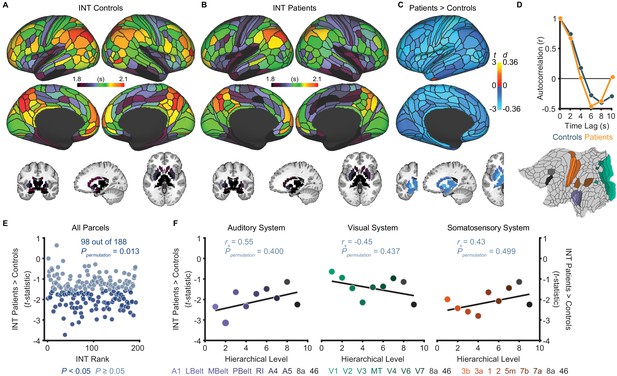
Exploratory analyses show that patients with schizophrenia exhibit widespread reductions of intrinsic neural timescales compared to healthy controls.
(A) Parcellated group-averaged intrinsic neural timescale (INT) map for healthy controls (N = 158). (B) Parcellated group-averaged INT map for patients with schizophrenia (N = 127). (C) t-statistic (Cohen’s d) map showing the contrast of patients greater than controls. Across most parcels, INT is shorter in patients than controls in a regression model (M1exploratory; Materials and methods) controlling for age, gender, mean framewise displacement, and sample-acquisition site (overall effect of diagnosis: 98 out of 188 parcels, Ppermutation = 0.013). Only the left hemisphere is shown because statistical analyses were performed after averaging the values in each parcel across the left and right hemispheres. (D) To illustrate the effect of reduced INT in patients with schizophrenia, the group-averaged, whole-brain-averaged autocorrelation functions were estimated from subjects with fMRI data acquired with the same repetition time (top; controls: N = 132; patients: N = 101). The group-averaged autocorrelation function for patients crosses the zero point on the y-axis (i.e. autocorrelation coefficient = 0) sooner than in controls, demonstrating the global reduction of INT in patients. The flattened cortex shows the parcels in the auditory, visual, and somatosensory hierarchies for reference (bottom). (E) Scatterplot showing t-statistic values for group differences from the regression model (M1exploratory), plotted as a function of the INT rank (determined from the group-averaged INT map from HCP subjects). Each datapoint represents one parcel. (F) Scatterplots showing t-statistic values from parcels within the auditory (left), visual (middle), and somatosensory (right) hierarchies plotted as a function of hierarchical level. No hierarchical-gradient effects of schizophrenia diagnosis were observed. LBelt, lateral belt; MBelt, medial belt; PBelt, parabelt; RI, retroinsular cortex; MT, middle temproal area.
-
Figure 2—source data 1
Data and code to reproduce Figure 2.
- https://cdn.elifesciences.org/articles/56151/elife-56151-fig2-data1-v1.zip
Figure 2—figure supplement 1
Voxelwise analysis of intrinsic neural timescales in schizophrenia versus health.
Scatterplot showing t-statistic values from a regression model predicting intrinsic neural timescale (INT) controlling for age, gender, mean framewise displacement, and data collection site, plotted as a function of the INT rank. Each datapoint represents one voxel. We repeated the exploratory analysis of INT in patients with schizophrenia versus healthy controls at the level of individual voxels. Only voxels that fell within the 188 parcels were included in this analysis. Similar results were observed as reported in the Main Text (Figure 3E) where we investigated effects at the level of parcels. Relative to controls, patients with schizophrenia exhibited a small-to-moderate but widespread reduction of INT (overall effect of diagnosis: 5,511 out of 27,884 voxels, Ppermutation = 0.020;). A non-significant number of voxels also showed significantly longer INT in patients with schizophrenia compared to healthy controls (93 out of 27,884 voxels, Ppermutation = 0.49).
Figure 2—figure supplement 2
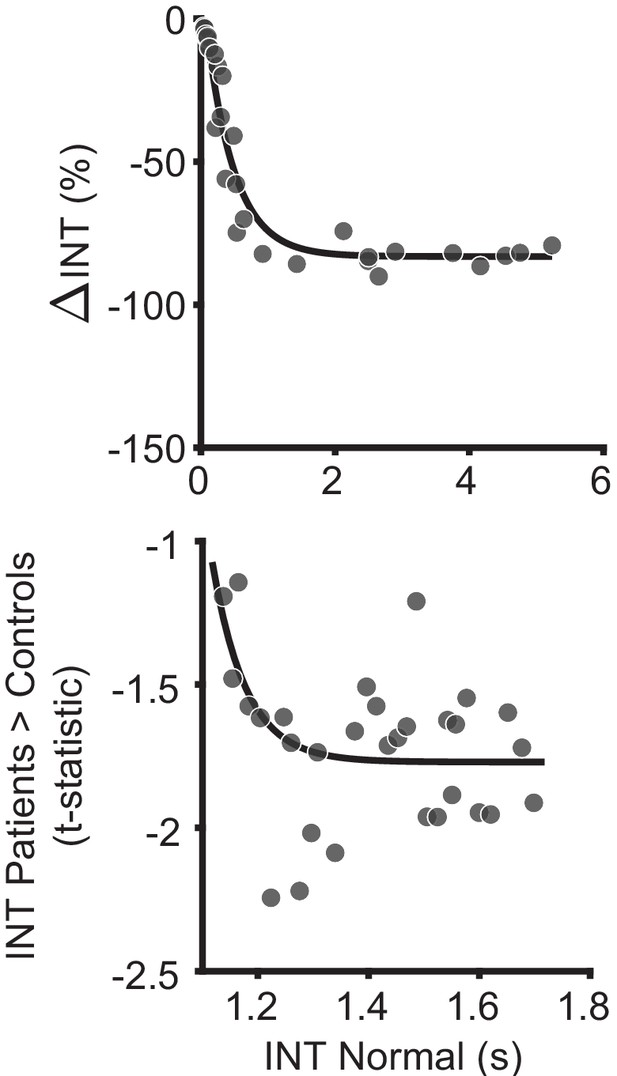
Biophysical model simulation of reduced intrinsic neural timescales in schizophrenia versus health.
An in silico simulation using a large-scale biophysical model suggested that the globally reduced intrinsic neural timescales (INT) observed in patients with schizophrenia could be neuronally implemented by globally reduced E/I ratio. Scatterplot showing the difference in INT values estimated for the reference (healthy) simulated scenario and the globally reduced excitatory-to-excitatory recurrent connection strength (reduced E/I ratio); each data point denotes 1 of the 29 nodes (top). Relative to the reference scenario, reduced excitatory-to-excitatory recurrent connection strength lead to a global reduction of INT values with the effect becoming more pronounced for regions with longer timescales in the healthy condition. The data are well described by an exponential model (R2 = 0.94). Scatterplot showin the t-statistic values from a regression model (M1exploratory) predicting INT group differences controlling for age, gender, mean framewise displacement, and data collection site, plotted as a function of the INT value in healthy subjects (determined from group-averaged INT map from HCP subjects to reduce circularity); each data point denotes the average of six parcels along the INT hierarchy for a similar number of data points as the biophysical model results (bottom). Similar to the biophysical model simulation, the data are better fit by an exponential model (Matlab fitnlm: F2,28 = 10.3, P = 0.003; BIC = 4.8), than a linear model (Matlab fitnlm: F1,29 = 1.4, P = 0.25; BIC = 9.3). Similar results are observed when no binning of the data is performed (exponential model: F2,185 = 8.3, P = 0.005; BIC = 366.4; linear model: F1,186 = 0.8, P = 0.38; BIC = 368.6). The findings are similar to a recent study that recapitulated the behavior of macaque monkeys on an evidence-varying decision-making task following intramuscular administration of a subanesthetic dose of ketamine by reducing the strength of the couplings to the excitatory population from the local excitatory population () by 1.75% to achieve a global reduction of E/I ratio (Cavanagh et al., 2019). This is consistent with the NMDA-receptor hypofunction hypothesis of schizophrenia (Corlett et al., 2011; Kehrer et al., 2008; Krystal et al., 2003; Lisman et al., 2008; Olney and Farber, 1995), and the use of ketamine as a model of schizophrenia (Becker et al., 2003; Corlett et al., 2011; Frohlich and Van Horn, 2014; Krystal et al., 1994). Furthermore, our biophysical model results support recent evidence of how global changes can preferentially affect higher order brain regions (Yang et al., 2016); and our in vivo results lend additional (although preliminary) evidence.
Figure 3 with 5 supplements
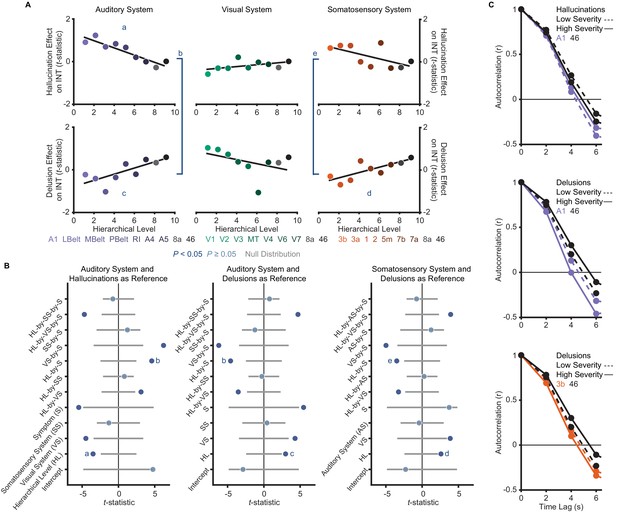
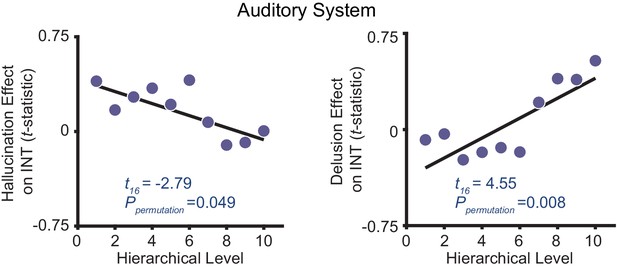
A priori analyses show that hallucinations and delusions exhibit distinct hierarchical-gradient effects on intrinsic neural timescales in the auditory and somatosensory systems.
(A) Scatterplots showing t-statistic values from a regression model (M1primary; Materials and methods) including all seven symptoms and controlling for age, gender, mean framewise displacement, and sample-acquisition site for hallucination-severity (top) and delusion-severity (bottom) effects from parcels within the auditory (left), visual (middle), or somatosensory (right) systems plotted as a function of hierarchical level (using PFC-extended winning hierarchies; Figure 1). (B) Summary of results from a model (M2; Materials and methods) including symptom-severity effect (hallucinations or delusions), hierarchical level, sensory system (auditory, visual, or somatosensory), and their interactions. These results demonstrate: (1) in the auditory system, a significant difference in the relationship between hallucination severity and hierarchical level versus that for delusion severity and hierarchical level (b); (2) in the auditory system, significant hierarchical-gradient effects of hallucination severity (a) and delusion severity (c); (3) in the somatosensory system, a significant difference in the relationship between hallucination severity and hierarchical level versus that for delusion severity and hierarchical level (e); and (4) in the somatosensory system, a significant hierarchical-gradient effect of delusion severity (d). Note that different symptoms and systems were used as references (implicit variable) across three plots to show each of the relevant effects which were tested within a single model (M2). Null distributions were generated by randomly permuting symptom-severity scores across patients in M1primary (2.5th – 97.5th percentiles shown). (C) To illustrate the effects, the group-averaged autocorrelation functions were estimated from subjects with fMRI data acquired with the same repetition time (N = 10 for each group). High-severity patients were the 10 subjects with the highest residual symptom scores after regressing out all other symptoms; low-severity patients were the 10 subjects with the lowest residual symptom scores. The group-averaged autocorrelation functions are shown for high-severity (solid lines) and low-severity (dashed lines) hallucination patients from low and high levels of the auditory hierarchy (A1 and area 46, top). The group-averaged autocorrelation functions are also shown for high-severity and low-severity delusion patients from low and high levels of the auditory hierarchy (middle). Finally, the group-averaged autocorrelation functions are shown for high-severity and low-severity delusion patients from low and high levels of the somatosensory hierarchy (area 3b and area 46, bottom). These plots depict a compression of the auditory hierarchical gradient in high-severity hallucination patients and, instead, an expansion of both the auditory and somatosensory hierarchical gradients in high-severity delusion patients. LBelt, lateral belt; MBelt, medial belt; PBelt, parabelt; RI, retroinsular cortex; MT, middle temproal area.
-
Figure 3—source data 1
Data and code to reproduce Figure 3.
- https://cdn.elifesciences.org/articles/56151/elife-56151-fig3-data1-v1.zip
Figure 3—figure supplement 1
Controlling for antipsychotic dose does not change the distinct hierarchical-gradient effects of hallucination and delusion severity in the auditory and somatosensory systems.
(A) Scatterplots showing t-statistic values from a regression model including all seven symptoms and and controlling for age, gender, mean framewise displacement, and sample-acquisition site for hallucination-severity (top), delusion-severity (middle), and dose (bottom) effects from parcels within the auditory (left), visual (middle), or somatosensory (right) hierarchies plotted as a function of hierarchical level. (B) Summary of results from a model including symptom-severity effect (hallucination or delusion), hierarchical level, sensory system (auditory, visual, or somatosensory), and their interactions. We repeated the main analysis comparing the effects of hallucination and delusion severity when including antipsychotic dose as a covariate. Only 109 of the 127 patients had available data for chlorpromazine equivalents. All results were similar to those reported in the Main Text where the effect of medication dose was not controlled for. The model explaining symptom effects and their differences by hierarchical-level and their interaction by symptoms and sensory system was significant (omnibus F11,41 = 22.4, p<10−13). Critically, we found significant hierarchical-gradient effects that differed between hallucinations and delusions (auditory system symptom-by-hierarchical-level interaction: t42 = 4.48, Ppermutation = 0.002; visual: t42 = −0.88, Ppermutation = 0.560; and somatosensory: t42 = 3.92, Ppermutation = 0.001). In the auditory system, this effect was driven by significant hierarchical-gradient effects in opposite directions for hallucinations (hierarchical-level effect: t42 = −3.40, Ppermutation = 0.013) and delusions (hierarchical-level effect: t42 = 2.94, Ppermutation = 0.028). In the somatosensory system, this effect was driven by a trend-level negative hierarchical-gradient effect for hallucinations (hierarchical-level effect: t42 = −2.25, Ppermutation = 0.064) and a significant positive hierarchical-gradient effect for delusions (hierarchical-level effect: t42 = 3.30, Ppermutation = 0.017).
Figure 3—figure supplement 2
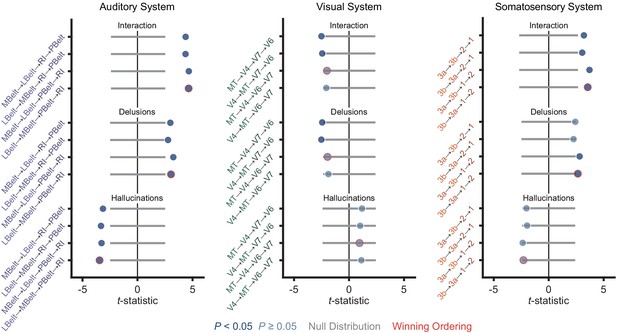
Distinct hierarchical-gradient effects of hallucinations and delusions are robust to the choice of sensory hierarchies.
Summary of results from a model including symptom-severity effect (hallucination or delusion), hierarchical level, sensory system (auditory, visual, or somatosensory), and their interactions for each of the four sensory cortex hierarchies tested for the auditory (left), visual (middle), and somatosensory (right) systems during Selection and Multimodal Validation of Neural Hierarchies. For the auditory system, A1 was always the lowest order region while A4 and A5 were always the 6th and 7th level regions. For the visual system, V1, V2, and V3 were always the three lowest order regions. For the somatosensory system, 5m, 7b, and 7a were always the 5th, 6th, and 7th level regions, respectively. For all three sensory systems, areas 8A and 46 were always the two highest order regions. The winning orderings from the selection process (Figure 1) are outlined in red. Hierarchical-gradient effects of hallucinations (Hallucinations; bottom four), delusions (Delusions; middle four) and their interaction (Interaction; top four) are shown (from M2). For this analysis, one sensory system hierarchical-ordering was tested while the other two sensory system hierarchical-orderings were chosen to be the winning orderings. Null distributions were generated by randomly permuting symptom-severity scores across patients in M1primary (2.5th – 97.5th percentiles shown).
Figure 3—figure supplement 3
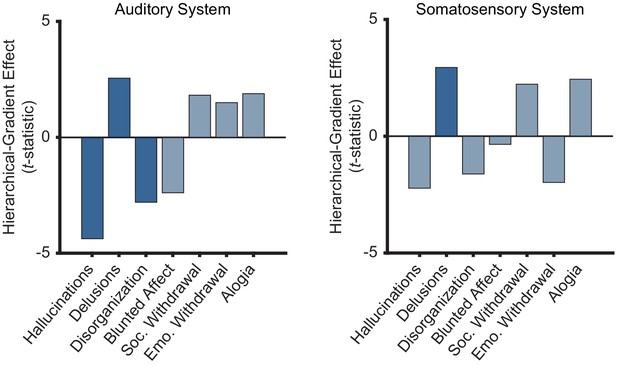
Only positive symptoms show hierarchical-gradient effects in the auditory system and only delusions show a hierarchical-gradient effect in the somatosensory system.
Bar graphs showing t-statistic values from a model including symptom-severity effect, heirarchical level, and their interaction (each symptom and sensory system was tested independently) for the hierarchical-gradient effect of each symptom in the auditory and somatosensory systems. In the auditory system, all three positive symptoms (including conceptual disorganization) show significant effects while none of the negative symptoms show significant effects. In the somatosensory system, only delusions show a significant effect, although hallucinations show the strongest negative effect. These results reflect some level of selectivity that should be examined in more detail in future studies. It is important to note that the perceptual-inference model of psychosis does not require these effects to be specific to hallucinations and delusions. Furthermore, an effect of conceptual disorganization—a positive symptom that unlike negative symptoms tends to correlate with hallucinations and delusions—may suggest extensions of the model to account for additional phenomena.
Figure 3—figure supplement 4
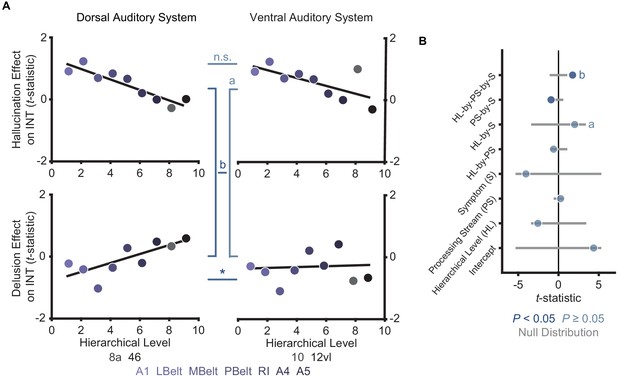
Comparison of hierarchical-gradient effects in the dorsal and ventral auditory systems.
(A) Scatterplots showing t-statistic values for hallucination-severity (top) or delusion-severity (bottom) effects from parcels within the dorsal auditory (left; areas 8a and 46) and ventral auditory (right; areas 10 and 12vl) hierarchies plotted as a function of hierarchical level. (B) Summary of results from a model including symptom-severity effect (hallucination or delusion), hierarchical level, sensory system (dorsal or ventral auditory system), and their interactions. These results demonstrate: (1) there is no significant difference in the hierarchical-gradient effect of hallucination severity between the dorsal and ventral auditory systems; (2) there is no significant difference in the relationship between hallucination severity and hierarchical level versus that for delusion severity and hierarchical level in the ventral auditory system (a); (3) there is a significant difference in the hierarchical-gradient effect of delusion severity between the dorsal and ventral auditory systems. These findings add to previous evidence suggesting that the dorsolateral prefrontal cortex (area 46; included in the dorsal but not the ventral auditory system) may play a key role in delusions.
Figure 3—figure supplement 5
Distinct hierarchical-gradient effects of hallucination and delusion severity in the auditory system are observed when using an anatomically agnostic definition of the hierarchy.
Scatterplots showing t-statistic values from a regressino model (M1primary; Materials and methods) including all seven symptoms and controlling for age, gender, mean framewise displacement, and sample-acquisition site for hallucination-severity (left) or delusion-severity (right) effects from bins consisting of the average from 60 voxels within the nine auditory system parcels (600 voxels total) as a function of hierarchical level. Voxels were first ranked using their corresponding intrinsic neural timescale (INT) value in the HCP dataset group-averaged INT map and then averaged within 10 equally spaced bins with increasing hierarchical level (i.e. the lowest level has the shortest average INT in the HCP dataset while the higheset hierarchical level has the longest average INT). Similar to our main analysis results, we observe a significant symptom-by-hierarchical-level interaction, a significant negative hierarchical-gradient effect for hallucinations, and a significant positive hierarchical-gradient effect for delusions.
Figure 4
Hallucination and delusion effects on intrinsic neural timescales are recapitulated by elevated excitation-inhibition ratios at different hierarchical levels.
(A) Scatterplots showing the difference in estimated intrinsic nerual timescale (INT) values between the three exemplary cases capturing extreme symptom profiles (‘hallucinations only’, ‘delusions only’, and ‘hallucinations and delusions’) with respect to the ‘no hallucinations or delusions’ exemplary case (in vivo ΔINT; fitted parcel-wise data from M1primary). The parcel data used for fitting the biophysical model are outlined in pink. Yellow arrowheads denote the hypothesized hierarchical level of the maximum excitation-inhibition (E/I) ratio increase. (B) Simplified schematic of a large-scale biophysical model of the macaque cortex and its variants (Materials and methods). The model consists of 29 nodes with local excitatory (red triangles) and inhibitory (blue circles) pools of neurons; only two nodes—high (top) and low (bottom) hierarchical levels—are shown for illustrative purposes. These nodes have both local (recurrent) and long-range (across-node) connections. Lightning bolts mark theoretical perturbations to the model. Thicker or thinner lines with respect to the reference scenario reflect increased or decreased connection strengths, respectively. Note that E/I ratio can be increased either by increasing local excitatory-to-excitatory connection strength or by decreasing local excitatory-to-inhibitory connection strength, but these scenarios were modeled individually. (C) Scatterplots showing the difference in simulated INT values between each of the three pathological biophysical models (‘elevated E/I ratio at low level’, ‘elevated E/I ratio at high level’, and ‘elevated E/I ratio at low and high levels’) with respect to the reference biophysical model (‘unaltered model’) using the best-fitting E/I ratio parameters (in silico ΔINT). By allowing the E/I ratios to vary, the biophysical model can recapitulate the in vivo INT changes with a negative (compressed) hierarchical-gradient effect for hallucinations, a positive (expanded) hierarchical-gradient effect for delusions, and an overall INT increase (without a manifest hierarchical-gradient effect) for the combined case of hallucinations and delusions. The visual hierarchy (V1, V2, V4, MT, 8l, and 46d) was used for these simulations given the lack of tract-tracing data for the auditory cortex—other levels of the visual cortex are omitted for the same reason—but the qualitative pattern of results applies to hierarchical-gradient effects in any given sensory system. Yellow arrowheads denote the hierarchical level of the maximum E/I ratio increase. (D) Scatterplots showing the fitted changes to E/I ratios for the pathological biophysical models: the in vivo INT changes associated with hallucinations can be recapitulated by elevated E/I ratio at the lowest hierarchical level and those associated with delusions by elevated E/I ratio (of smaller magnitude) at the highest hierarchical level, with the addition of these two alterations capturing the changes in patients with both hallucinations and delusions. Note that E/I ratio in level 9 of the hierarchy was fixed to its value in the unaltered model to prevent model instability (Materials and methods). LBelt, lateral belt; MBelt, medial belt; PBelt, parabelt; RI, retroinsular cortex.
-
Figure 4—source data 1
Data and code to reproduce Figure 4.
- https://cdn.elifesciences.org/articles/56151/elife-56151-fig4-data1-v1.zip
Tables
Table 1
Participant characteristics.
| Variable | Healthy controls | Patients with schizophrenia | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BGS | COBRE | NMCH | UCLA | All | BGS | COBRE | NMCH | UCLA | All | ||
| N | 24 | 42 | 25 | 67 | 158 | 40 | 31 | 26 | 30 | 127 | |
| Age, mean (SD), y | 36.0 (13.1) | 33.9 (10.4) | 29.8 (7.2) | 32.3 (8.5) | 32.9 (9.7) | 31.1 (12.6) | 30.5 (11.9) | 30.5 (6.2) | 35.0 (8.9) | 31.8 (10.6) | |
| Male sex, No. (%) | 22 (92) | 34 (81) | 16 (64) | 54 (81) | 126 (80) | 38 (95) | 26 (84) | 19 (73) | 22 (73) | 105 (83) | |
| Framewise displacement*, mean (SD), mm | 0.15 (0.04) | 0.14 (0.05) | 0.14 (0.11) | 0.10 (0.04) | 0.13 (0.06) | 0.16 (0.06) | 0.17 (0.06) | 0.12 (0.06) | 0.13 (0.04) | 0.15 (0.06) | |
| Delusion score, mean (SD) | NA | NA | NA | NA | NA | 2.3 (1.6) | 1.7 (1.5) | 3.2 (1.9) | 2.5 (1.4) | 2.4 (1.7) | |
| Hallucination score, mean (SD) | NA | NA | NA | NA | NA | 2.1 (1.6) | 1.7 (1.4) | 2.9 (2.0) | 2.2 (1.6) | 2.2 (1.7) | |
| Conceptual disorganization score, mean (SD) | NA | NA | NA | NA | NA | 0.9 (1.3) | 0.6 (1.0) | 2.0 (1.6) | 1.4 (1.4) | 1.2 (1.4) | |
| Emotional withdrawal score, mean (SD) | NA | NA | NA | NA | NA | 1.8 (1.2) | 1.2 (1.3) | 3.4 (1.7) | 2.3 (1.5) | 2.1 (1.6) | |
| Social withdrawal score, mean (SD) | NA | NA | NA | NA | NA | 1.8 (1.4) | 1.3 (1.4) | 3.2 (1.7) | 2.7 (1.6) | 2.2 (1.6) | |
| Blunted affect score, mean (SD) | NA | NA | NA | NA | NA | 1.8 (1.6) | 1.6 (1.5) | 3.3 (1.6) | 1.1 (1.1) | 1.9 (1.6) | |
| Alogia score, mean (SD) | NA | NA | NA | NA | NA | 1.3 (1.6) | 1.2 (1.4) | 2.1 (1.7) | 0.9 (1.6) | 1.3 (1.6) | |
-
*Framewise displacement values were estimated after motion censoring.
BGS, BrainGluSchi; NMCH, NMorphCH; SD, standard deviation.
-
Table 1—source data 1
Raw data for each individual subject in Table 1.
- https://cdn.elifesciences.org/articles/56151/elife-56151-table1-data1-v1.xlsx
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Distinct hierarchical alterations of intrinsic neural timescales account for different manifestations of psychosis
eLife 9:e56151.
https://doi.org/10.7554/eLife.56151
