Figures and data in Nutrient levels and trade-offs control diversity in a serial dilution ecosystem

Figures
Tables
Additional files

18 figures, 1 table and 1 additional file

Figures

Figure 1

Download asset Open asset

Illustration of serial dilution resource-competition model.

(A) Serial dilution protocol. Each cycle of batch growth begins with a cellular biomass density $ρ_{0}$ and total nutrient concentration c₀. The system evolves according to Equations 2-3 until nutrients are completely consumed. A sample of the total biomass is then used to inoculate the next batch again at density $ρ_{0}$ . (B) Representation of particular enzyme-allocation strategies ${α_{σ}}$ (colored circles) and nutrient supply composition $c_{i} / c_{0}$ (black diamond) on a 2-nutrient simplex, where the right endpoint corresponds to $c_{1} / c_{0} = 1$ . (C) Representation of particular strategies (circles) and nutrient supply (black diamond) on a 3-nutrient simplex. Dashed blue - the convex hull of the enzyme-allocation strategies. Here, the nutrient supply (black diamond) is inside the convex hull, implying coexistence of all species in the chemostat limit (see text).

Figure 2

Download asset Open asset

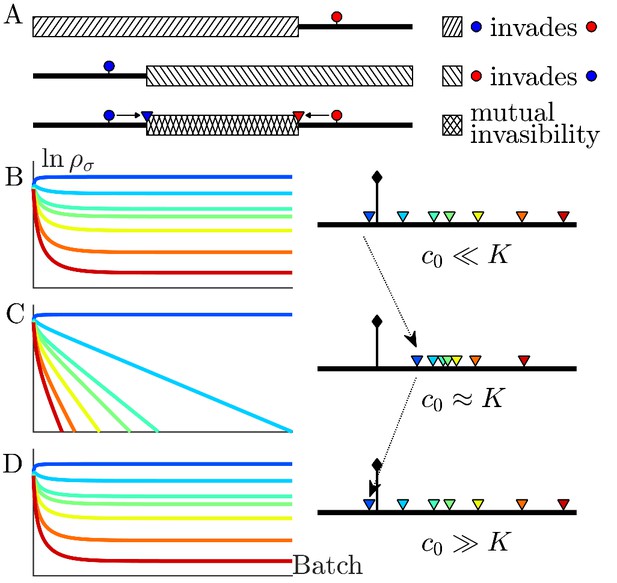
The nutrient bolus size c₀ affects the relative abundance of species and even their coexistence at steady state.

(A) Schematic of the mutual invasibility condition for two species and two nutrients. Top: The red species can be invaded by any species with a strategy to its left if the supply lies in the region marked by the hatched rectangle. Middle: Similarly, showing the supplies for which blue can be invaded by any species with a strategy to its right. Bottom: The intersection defines a mutual invasibility region of supplies for which the two species red and blue will coexist. Triangles mark the boundaries of this coexistence region. (**B–D**) Example of the effect of c₀ on coexistence for more than two species: the approach to steady state, showing $ρ_{σ}$ versus batch number (left column) with the corresponding c₀-dependent remapping of coexistence boundaries (right column). (B) For the chemostat limit $c_{0} ≪ K$ , where K is the Monod constant for nutrient uptake, the triangles marking coexistence boundaries coincide with the species’ strategies, $α_{σ}$ . (C) For $c_{0} \approx K$ the triangles are remapped towards the center of the simplex compared to the strategies ${α_{σ}}$ . In this example the nutrient supply (black diamond) ends up outside the coexistence boundaries, so only one species survives. (D) For $c_{0} ≫ K$ the triangles again coincide with the strategies ${α_{σ}}$ , leading again to coexistence.

Figure 3

Download asset Open asset

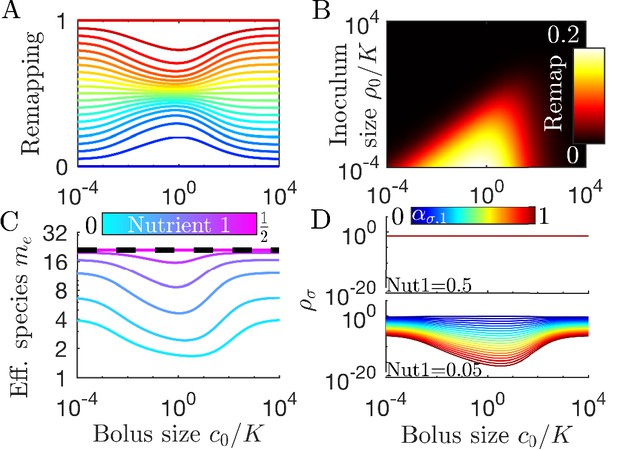
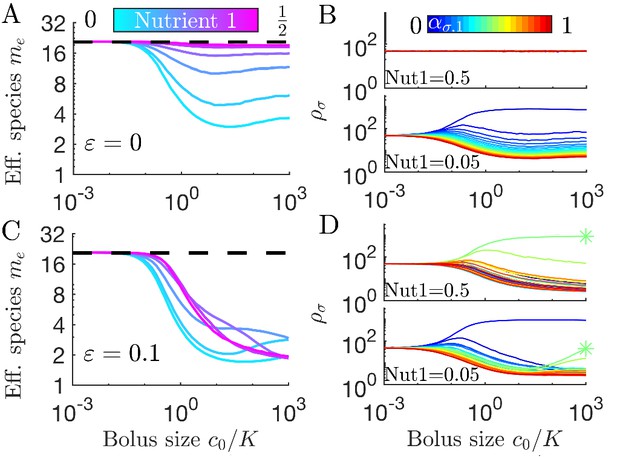
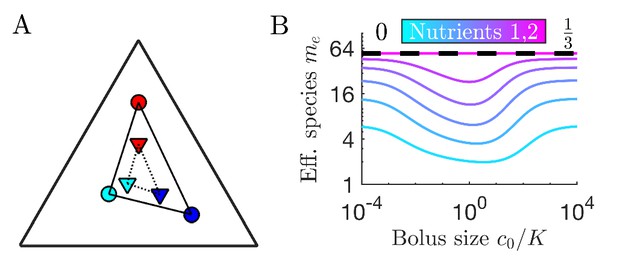
Remapping of strategies at finite nutrient supply generally reduces species diversity.

(A) As shown for the case of two nutrients, the remapping of strategies (i.e., the shift of coexistence boundaries) is non-monotonic with nutrient bolus size c₀ (colors indicate 21 equally spaced strategies). (B) Heat map of the extent of remapping for strategy $(0.2, 0.8)$ as a function of nutrient bolus size $c_{0} / K$ and inoculum size $ρ_{0} / K$ . (C) Steady-state effective number of species m_e as a function of bolus size $c_{0} / K$ with equal initial inocula adding up to $ρ_{0} / K = 10^{- 3}$ ; the same initial conditions apply for panels *C-D*. Colors correspond to different nutrient supply compositions $c_{1} / (c_{1} + c_{2})$ . Dashed black line: maximum diversity (equal species abundances) is attained when nutrient composition is $(0.5, 0.5)$ . (D) Steady-state species abundances ${ρ_{σ}}$ for nutrient composition $(0.5, 0.5)$ (top) and $(0.05, 0.95)$ (bottom).

Figure 4

Download asset Open asset

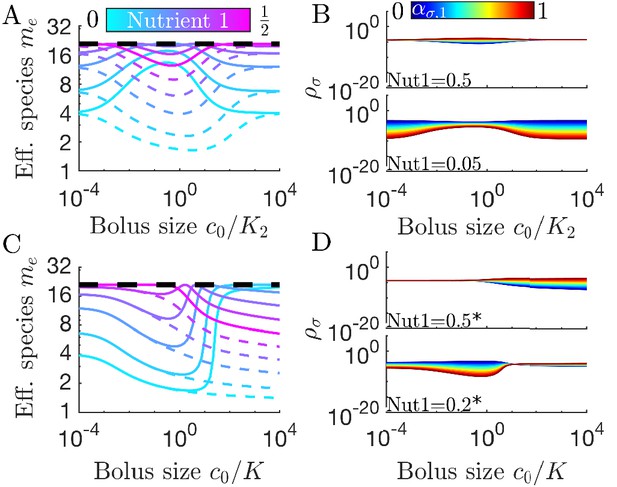
Differences in enzymes affinities, K_i, and nutrient yields, Y_i, lead to different relationships between diversity and bolus size.

(A) Steady-state effective number of species m_e as a function of bolus size $c_{0} / K_{2}$ , as in Figure 3C, but with $K_{1} = 10^{- 3}$ and $K_{2} = ρ_{0} = 1$ . Colors correspond to different nutrient supply compositions, solid curves for $c_{1} / c_{0} \in [0, 0.5]$ and dashed curves for $c_{1} / c_{0} \in [0.5, 1]$ . Dashed black line: maximum diversity (equal species abundances) is no longer attained when nutrient composition is $(0.5, 0.5)$ . (B) Steady-state species abundances ${ρ_{σ}}$ for nutrient composition $(0.5, 0.5)$ (top) and $(0.05, 0.95)$ (bottom), as in Figure 3D. (C) Steady-state effective number of species m_e as a function of bolus size $c_{0} / K$ , as in Figure 3C, but with $Y_{1} = 10$ and $Y_{2} = ρ_{0} = 1$ . Note that the nutrient compositions are normalized to yield such that $({0.5}^{*}, {0.5}^{*})$ is actually $(0.5 / Y_{1}, 0.5 / Y_{2})$ . Colors the same as in A. (D) Steady-state species abundances ${ρ_{σ}}$ for nutrient composition $({0.5}^{*}, {0.5}^{*})$ (top) and $({0.2}^{*}, {0.8}^{*})$ (bottom).

Figure 5

Download asset Open asset

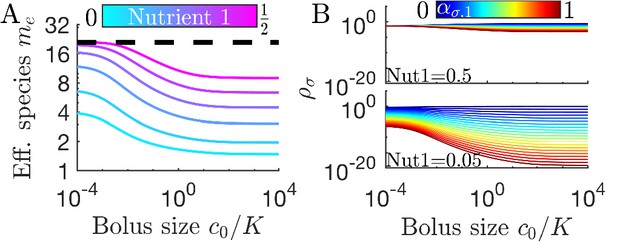
Cross-feeding alters the relationship between diversity and bolus size.

(A) Steady-state effective number of species m_e as a function of bolus size, as in Figure 3C but with two trophic layers, with Nutrient 1 a byproduct of metabolizing Nutrient 2. The byproduct fraction $Γ$ is chosen so that Nutrient 1 is produced at fractions according to the colorbar in A. (B) Steady-state species abundances ${ρ_{σ}}$ for nutrient composition $(0.5, 0.5)$ (top) and $(0.05, 0.95)$ (bottom), as in Figure 3D.

Figure 6

Download asset Open asset

Diversity of small communities with migration.

Each batch was inoculated with 1008 cells: 958 cells sampled without replacement from the previous batch, 50 cells sampled from 21 equally abundant, equally spaced strategies. (A) Effective number of species m_e for different compositions of two nutrients (colors) as a function of nutrient bolus size $c_{0} / K$ . (B) Average steady-state species abundances ${ρ_{σ}}$ for nutrient composition $(0.5, 0.5)$ (top) and $(0.05, 0.95)$ (bottom). (C) As A, but with random species-specific total enzyme budget specified by $ε = 0.1$ . (D) As B but with species-specific enzyme budgets from C. Asterisk (*) indicates the species with the largest enzyme budget.

Appendix 4—figure 1

Download asset Open asset

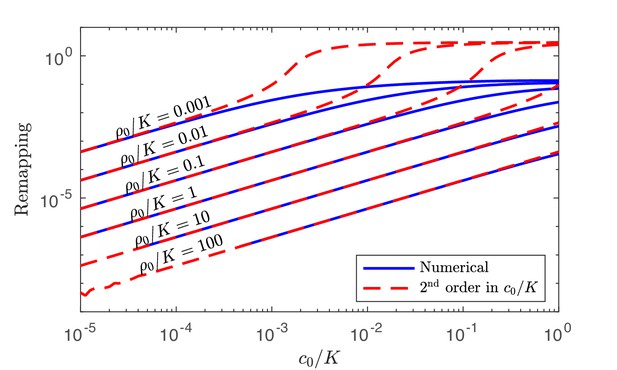
Numerical solution and analytical perturbation theory results for remapping of the coexistence boundaries at low c₀.

The analytic solution is derived from $\forall i : I_{i} = const$ using the second-order expansion in Equation 40.

Appendix 4—figure 2

Download asset Open asset

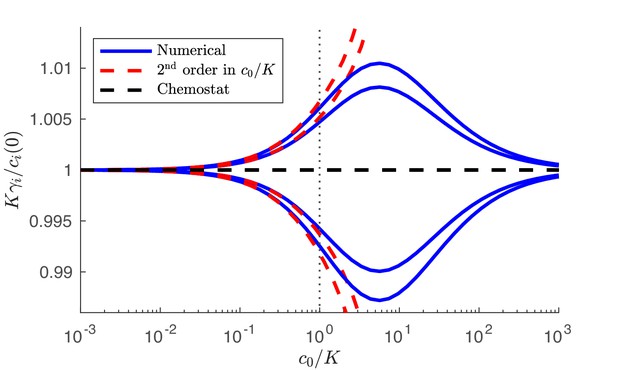
Numerical solution and analytical perturbation theory results for the steady-state solution manifold at low c₀.

The analytic solution is derived from Equation 47 and the chemostat solution is from Equation 43. *Outer curves*: 3 species with strategies ${(0.1, 0.9), (0.45, 0.55), (1, 0)}$ . *Inner curves*: 3 species with strategies ${(0, 1), (0.5, 0.5), (1, 0)}$ . In both cases, $ρ_{0} / K = 1$ and the nutrient supply is $(0.55, 0.45)$ .

Appendix 6—figure 1

Download asset Open asset

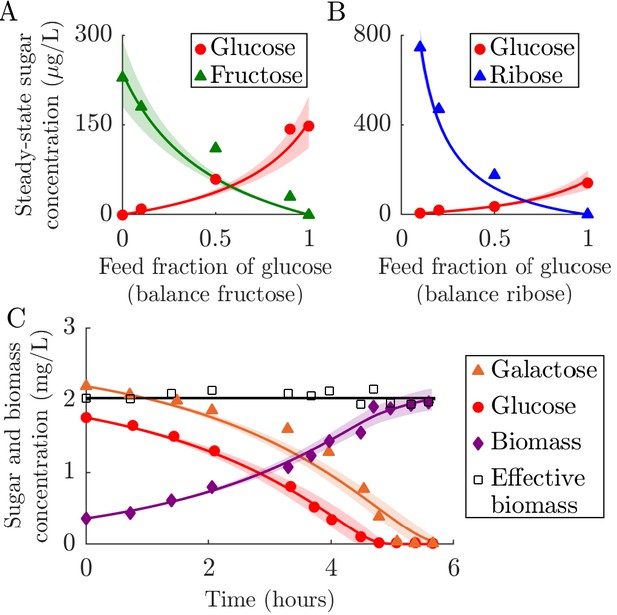
Fitting of fixed-enzyme-budget model to experimental data.

(**A–B**) Fit of the chemostat version of the model to data from chemostat experiments from Lendenmann et al., 1996. The experimental data are steady-state concentrations of sugars in *E. coli* chemostats supplied with different mixtures of glucose, fructose, and ribose. The strategy $α_{i}$ for each sugar is inferred, whereas all other parameters are derived from the experimental conditions and measurements. The solid curves show the model prediction, with the shaded region marking the 95% prediction bound (see Appendix 1 for details). (A) Comparison of model to data from chemostats supplied with glucose and fructose with a constant total feed concentration of 100 mg/L. (B) Comparison of model to data from chemostats supplied with glucose and ribose with a constant total feed concentration of 100 mg/L. (C) Comparison of serial dilution model fit to batch growth data from Egli et al., 1993. Solid curves are model predictions and the shaded area is the 95% prediction bound. ‘Effective biomass’ refers to the total biomass within the system: $M (t) = ρ (t) + Y (c_{gluc} (t) + c_{gal} (t))$ . Since the data for the three timeseries were measured at slightly different times, the effective biomass for the experimental data was obtained by linear interpolation of the data points. The inferred parameters were the strategy ( $α_{1}$ , $α_{2}$ ) for the two sugars, glucose and galactose, and the yield Y.

Appendix 6—figure 2

Download asset Open asset

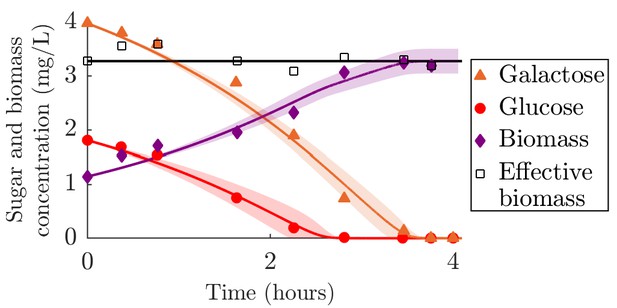
Comparison of serial dilution model fit to batch growth data from Lendenmann et al., 2000.

This data is similar to that in Appendix 6—figure 1C, except that the inoculum was taken from galactose-limited conditions instead of glucose limited conditions. Solid curves are model predictions and the shaded area is the 95% prediction bound (see Appendix 1 for details). ‘Effective biomass’ refers to the total biomass within the system: $M (t) = ρ (t) + Y (c_{1} (t) + c_{2} (t))$ . Since the data for the three timeseries were measured at slightly different times, the effective for the experimental data was obtained by linear interpolation of the data points. The inferred parameters were the strategy ( $α_{2}$ , $α_{2}$ ) for the two sugars, glucose and galactose, and the yield Y. The estimated $α_{i}$ , measured in units of (mg sugar)(mg biomass)^–1h^–1, were 0.43 ± 0.06 and 0.57 ± 0.04 for glucose and galactose, respectively. The estimated yield of 0.37 ± 0.03 was similar to that inferred in Appendix 6—figure 1C.

Appendix 7—figure 1

Download asset Open asset

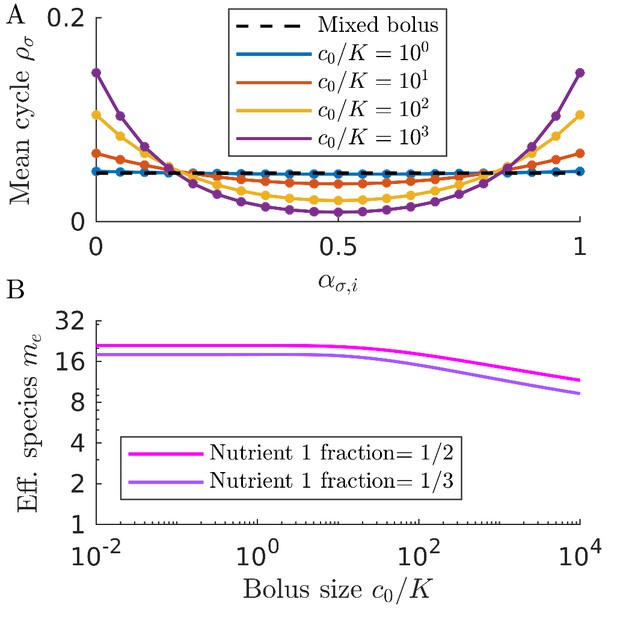
Serial dilution model with cycling bolus compositions.

In this work we largely consider the case of nutrient boli that contain a defined mixture of nutrient. However, in nature the nutrient boli may not themselves contain a mixture of nutrients, but instead approach a mixed distribution of nutrients over time. To explore we compare the case of mixed boli with that of cycled single-nutrient boli that are varied in time to approach a mixed distribution. (A) Mean steady-state population abundances in communities supplied with boli containing an equal mixture of two nutrients (dashed line) or alternating boli each containing a single nutrient (solid curves). Population abundances are averaged over a single cycle. The community is composed of 21 equally-spaced species. For the cycling bolus case, the species that are more specialized for either nutrient become more abundant due to a ‘single-nutrient’ early-bird effect as $c_{0} / K$ is increased. (B) Effective number of species as a function of $c_{0} / K$ for communities supplied with cycling single nutrient boli. Communities consist of 21 equally spaced strategies are supplied a cycle of boli approaching an average nutrient 1 fraction of 1/2 or 1/3. The effective number of species decreases as a function of $c_{0} / K$ due to the ‘single-nutrient’ early-bird effect.

Appendix 7—figure 2

Download asset Open asset

Serial dilution model with incomplete nutrient depletion.

We have thus far assumed that batches run until the nutrient is entirely depleted. However, batches might be terminated before nutrients are completely depleted. Here we characterize the steady state of a community of 21 equally spaced species when the batch is terminated early such that $\sum c_{i} / c_{0} = Δ$ , where $Δ$ is the fraction of nutrient remaining at the end of the batch. In these simulations, $ρ_{0} = c_{0} = K = 1$ , with nutrient composition $(1 / 3, 2 / 3)$ . Batches are repeated until either a relative error tolerance is met (less than $10^{- 8}$ change between batches) or 40,000 batches have elapsed (the large batch limit is there to account for possible critical slowing down). As can be seen, coexistence is fairly robust with respect to incomplete nutrient consumption until $Δ \approx 0.45$ after which point diversity rapidly collapses. The reduction in diversity in the system can be explained by the early-bird effect. In a batch where complete nutrient depletion occurs, the early bird gains an early advantage by rapidly depleting the more abundant nutrient, and then is able to consume a larger share of the non-abundant nutrient. Therefore, if the batch is terminated early, the amount of non-abundant nutrient consumed within the batch becomes smaller. While this makes the early bird less able to consume the non-abundant nutrient, it more severely impacts non-early-bird species, as their growth is more reliant on the non-abundant nutrient. As the batch terminates earlier and earlier, the system effectively becomes competition for a single nutrient (the more abundant one). Thus, the most fit early bird (the specialist for the more abundant nutrient) completely takes over the population.

Appendix 7—figure 3

Download asset Open asset

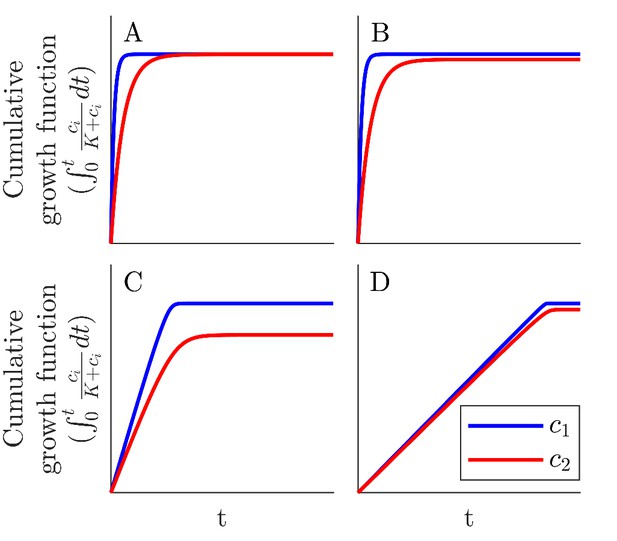
Cumulative growth function integrals at different values of $c_{0} / K$ for a species with $α_{σ} = (0.8, 0.2)$ growing with nutrient supplied with proportion $(0.8, 0.2)$ and initial population $ρ_{0} = 1$ .

(A) Cumulative growth integrals with $c_{0} / K = 0.001$ . (B) Cumulative growth integrals with $c_{0} / K = 0.1$ . (C) Cumulative growth integrals with $c_{0} / K = 10$ . (D) Cumulative growth integrals with $c_{0} / K = 100$ . When $c_{0} ≪ K$ and $c_{0} ≪ ρ_{0}$ , the consumption rate of each nutrient is proportional to its own abundance, $c_{i} / (K + c_{i}) \approx c_{i} / K$ , and there is little relative change in biomass, $ρ (t) \approx ρ_{0}$ . The more abundant nutrient is consumed faster (since the strategy is matched to nutrient proportions) and the majority of it is consumed quickly. The less abundant nutrient is consumed more slowly and a significant portion of it remains after the more abundant nutrient is almost completely depleted. In this way, the growth timecourse integrals are balanced to be equal. Once c₀ increases relative to $ρ_{0}$ , but c₀ is not large compared to K this balance is broken. The more abundant nutrient will still be depleted quickly. However, now that c₀ is larger this initial consumption results in an increased abundance of the consumer. This means that the less abundant nutrient is depleted more quickly, leading a smaller growth timecourse integral for this nutrient relative to the more abundant nutrient. Thus, in this regime, the difference between the growth timecourse integrals increases with c₀. Restoring them to equality requires more equal starting distributions of nutrients. Once c₀ increases such that $c_{0} ≫ K$ and $c_{0} ≫ ρ_{0}$ , the increase in c₀ now drives the growth timecourse integrals towards equality. The growth function is now almost always saturated and this neutralizes the effect of one nutrient starting at a much larger concentration. There will now be a significant buildup of biomass before the nutrients are exhausted, meaning that the growth timecourses will subsequently drop very quickly. As the growth function becomes more and more saturated, the nutrients will be consumed in proportion to their strategy. Thus, the growth timecourse integrals will once again be equal since the strategies match the nutrient proportions and the 'crash' times will therefore be similar for both nutrients.

Appendix 7—figure 4

Download asset Open asset

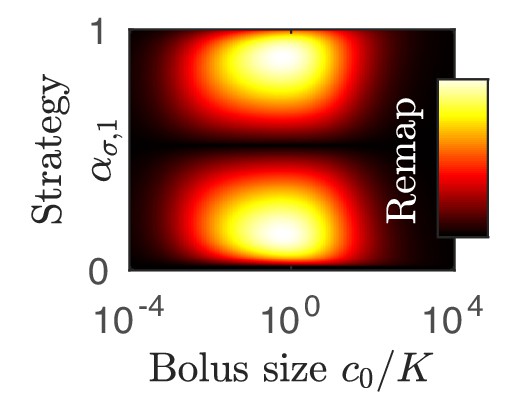
Dependence of coexistence boundary remapping on $c_{0} / K$ .

As a further exposition to Figure 3A in the main text, shown here is the difference between the remapped coexistence boundaries and the corresponding metabolic strategies as a function of $c_{0} / K$ and metabolic strategy with $ρ_{0} / K = 10^{- 3}$ .

Appendix 7—figure 5

Download asset Open asset

Serial dilution model with three nutrients.

(A) Example of remapping on the three-nutrient simplex, similar to Figure 2 from the main text. Here we show how the remapping analysis presented in the main text for two nutrients can be extended to three nutrients. Remapping of three strategies for $c_{0} / K = 1$ and $ρ_{0} = 10^{- 2}$ . Outer circles: strategies ${{\vec{α}}_{σ}}$ ; inner triangles: remapped nodes; lines connecting outer circles: supplies within this convex hull of strategies lead to coexistence of all species in the chemostat regime $c_{0} / K ≪ 1$ ; dashes connecting inner circles: approximate remapped convex hull boundary defining region of supplies leading to coexistence for $c_{0} / K = 1$ . Note that, as in the two-nutrient case, the strategies map inwards on the simplex for $c_{0} / K \approx 1$ . (B) Steady-state effective number of species m_e versus $c_{0} / K$ for equal initial inocula of 64 species equally spaced throughout the triangular simplex competing for three nutrients. Effective number of species shows the same trend of loss in diversity when $c_{0} / K \approx 1$ as in the two-nutrient case in Figure 2C.

Appendix 7—figure 6

Download asset Open asset

Large differences between K_i values can lead to multi-peaked relationships between diversity and bolus size.

Here, we present a magnified version of the community growing with nutrient compositon $(0.3, 0.7)$ in Figure 4A, with $K_{1} = 10^{- 3}$ and $K_{2} = ρ_{0} = 1$ . The change in the identity of the early bird can explain how multiple diversity peaks occur in the curve shown. If the system is near maximum diversity in the chemostat limit and the early-bird effect favors the species that is disadvantaged in the chemostat, the system will initially be driven towards maximum diversity with increasing c₀. However, as the early-bird effect continues to strengthen, the formerly disadvantaged species will begin to dominate the community, lowering community diversity. Then, as $c_{0}$ continues to increase and the early-bird effect weakens, the early bird’s dominance will wane, again driving the system towards maximum diversity. Finally, the non-early-bird species will overtake the early bird in the high c₀ chemostat limit, driving diversity back downwards.

Appendix 7—figure 7

Download asset Open asset

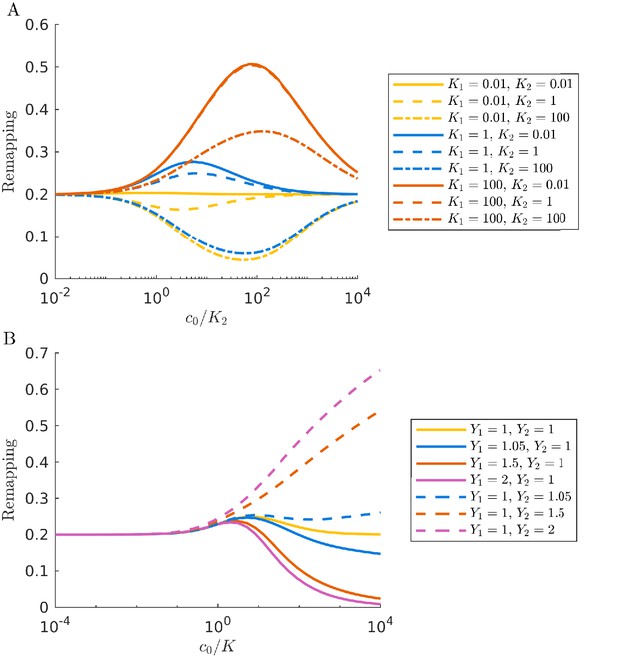
Remapping in the serial dilution model with unequal K_i and Y_i.

Here we show that varying the values of K_i and Y_i can influence the direction and magnitude of the remapping, using $α_{σ 1} = 0.2$ with $ρ_{0} = 1$ as an example. (A) Remapping with different combinations of K_i. The strategy we are examining devotes most of its enzyme budget to consuming nutrient 2. When there is a large different in K_i that favors nutrient 2, inward remapping is enhanced. When there is a large difference that favors nutrient 1, outward remapping is enhanced. Eventually, the remapping returns to the chemostat limit. (B): Remapping with different combinations of Y_i. Note that when yields are variable the condition for the remapped point is $I_{i} = \int_{0}^{\infty} Y_{i} \frac{c_{i}}{K_{i} + c_{i}} 𝑑 t = const$ . The remapped points shown are normalized to yield (if the remapped point is $(x, 1 - x)$ the normalized form is $(x^{*}, 1 - x^{*})$ where $x^{*} = \frac{Y_{1} x}{Y_{1} x + (1 - x) Y_{2}}$ ). Similar to the unequal K_i case, inward remapping is enhanced when there are large differences in Y_i favoring nutrient 2. When the Y_i favor nutrient 1, outward remapping is enhanced. Unlike in the unequal Y_i case, the remapping does not return to the chemostat limit.

Appendix 7—figure 8

Download asset Open asset

Batch timecourses of a bitrophic model with only two species.

To further investigate the difference between the unitrophic and bitrophic scenarios, we consider a toy system with only two species, Species 1 with strategy $(0.05, 0.95)$ and Species 2 with strategy $(0.95, 0.05)$ . We set the byproduct matrix for perfect conversion, $Γ_{1, 2} = 1$ and the nutrient bolus composition so that only Nutrient 2 is provided. By the end of each batch, the same amounts of Nutrient 1 and Nutrient 2 have been consumed. (A) Simulations with constant $c_{0} / ρ_{0}$ and variable $c_{0} / K$ . The 'early-bird’ effect becomes stronger with decreasing $c_{0} / K$ , since this allows the dominant species to grow more before the byproduct can be readily consumed. (B) Simulations with variable $c_{0} / ρ_{0}$ and constant $c_{0} / K$ . The 'early-bird’ effect is stronger at higher $c_{0} / ρ_{0}$ because the larger amount of supplied nutrient allows the dominant species to build a large population which can then outcompete other species. Conversely, if instead of cross-feeding we were to supply in the nutrient bolus equal quantities of Nutrients 1 and 2, the result would be equal abundance of both species.

Tables

Appendix 1—table 1

Annotation glossary.

Symbol	Description
t	Time measured from the beginning of a batch
p	Number of nutrients
m	Number of species introduced at time $t = 0$
m_e	Effective number of species at steady state
i	$(1 \dots p)$ Latin index enumerating nutrients
$c_{i} (t)$	Time dependent concentration of nutrient i
c₀	$\sum_{i = 1}^{p} c_{i} (0)$ ; total nutrient concentration at time $t = 0$
K_i	Monod half-velocity constant for nutrient i
I_i	$\int_{0}^{\infty} \frac{c_{i}}{K_{i} + c_{i}} 𝑑 t$ ; nutrient Monod function time integral
Y_i	Biomass yield on nutrient i
$Δ$	The fraction of nutrient remaining at the end of the batch
s_i	Average rate that nutrient i is continuously supplied at the chemostat limit
$\tilde{δ}$	Average rate all nutrients are continuously supplied at the chemostat limit
δ	Continuous chemostat dilution rate at the chemostat limit
$σ, σ^{'}, \dots$	$(1 \dots m)$ Greek indices enumerating species
$ρ_{σ} (t)$	Species σ biomass density at time t since a start of the batch
${\vec{α}}_{σ}$	$(α_{σ, 1}, \dots, α_{σ, p})$ ; enzyme allocation strategy for species σ
ε	Standard deviation in enzyme budget
E	$E = \sum_{i} α_{σ, i} = 1$ for $ε = 0$ ; enzyme budget
$Γ_{i, i^{'}}^{σ}$	Byproduct matrix converting nutrient $i^{'}$ to nutrient i
$j_{σ, i}$	Nutrient i consumption rate by species σ

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/57790/elife-57790-transrepform-v1.pdf
Download elife-57790-transrepform-v1.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Amir Erez
Jaime G Lopez
Benjamin G Weiner
Yigal Meir
Ned S Wingreen

(2020)

Nutrient levels and trade-offs control diversity in a serial dilution ecosystem

eLife 9:e57790.

https://doi.org/10.7554/eLife.57790

Share this article

Cite this article

Illustration of serial dilution resource-competition model.

The nutrient bolus size c0 affects the relative abundance of species and even their coexistence at steady state.

Remapping of strategies at finite nutrient supply generally reduces species diversity.

Differences in enzymes affinities, Ki, and nutrient yields, Yi, lead to different relationships between diversity and bolus size.

Cross-feeding alters the relationship between diversity and bolus size.

Diversity of small communities with migration.

Numerical solution and analytical perturbation theory results for remapping of the coexistence boundaries at low c0.

Numerical solution and analytical perturbation theory results for the steady-state solution manifold at low c0.

Fitting of fixed-enzyme-budget model to experimental data.

Comparison of serial dilution model fit to batch growth data from Lendenmann et al., 2000.

Serial dilution model with cycling bolus compositions.

Serial dilution model with incomplete nutrient depletion.

Cumulative growth function integrals at different values of c0/K for a species with ασ=(0.8,0.2) growing with nutrient supplied with proportion (0.8,0.2) and initial population ρ0=1.

Dependence of coexistence boundary remapping on c0/K.

Serial dilution model with three nutrients.

Large differences between Ki values can lead to multi-peaked relationships between diversity and bolus size.

Remapping in the serial dilution model with unequal Ki and Yi.

Batch timecourses of a bitrophic model with only two species.

Annotation glossary.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

The nutrient bolus size c₀ affects the relative abundance of species and even their coexistence at steady state.

Differences in enzymes affinities, K_i, and nutrient yields, Y_i, lead to different relationships between diversity and bolus size.

Numerical solution and analytical perturbation theory results for remapping of the coexistence boundaries at low c₀.

Numerical solution and analytical perturbation theory results for the steady-state solution manifold at low c₀.

Cumulative growth function integrals at different values of $c_{0} / K$ for a species with $α_{σ} = (0.8, 0.2)$ growing with nutrient supplied with proportion $(0.8, 0.2)$ and initial population $ρ_{0} = 1$ .

Dependence of coexistence boundary remapping on $c_{0} / K$ .

Large differences between K_i values can lead to multi-peaked relationships between diversity and bolus size.

Remapping in the serial dilution model with unequal K_i and Y_i.