Firing rate-dependent phase responses of Purkinje cells support transient oscillations
- Computational Neuroscience Unit, Okinawa Institute of Science and Technology Graduate University, Japan
Figures
Figure 1 with 2 supplements
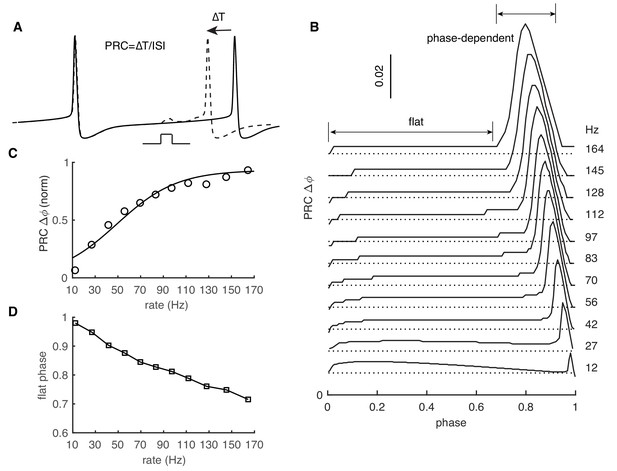
PRC exhibits strong rate adaptation in PC model.
(A) Schematic representation of the definition and computation of PRCs. The current pulse has a duration of 0.5 ms and an amplitude of 50 pA. Different spike rates were achieved by somatic current injection (Couto et al., 2015; Phoka et al., 2010). (B) The rate adaptation of the flat part and the phase-dependent PRC peak. (C) PRC peak amplitudes at different firing rates fitted by the Boltzmann function. (D) Duration of the flat phase at different firing rates.
Figure 1—figure supplement 1
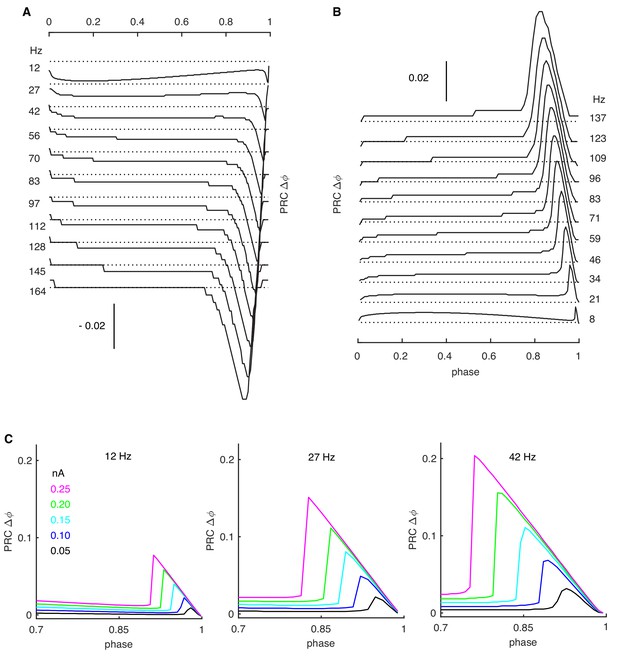
Rate-dependent PRCs.
(A) Negative stimulus-triggered responses (phase delay) parallel positive stimuli (see Figure 1). Onset-phases of phase-dependent responses shift left at high rates with gradually larger amplitudes. (B) The PC model with passive dendrites shows similar rate adaptation as in PC models with active dendrites (Figure 1). (C) Larger stimulus amplitudes increase the peak of the phase-dependent PRCs and shift their onset phases to the left. Simulation results at rates of 12-, 27- and 42 Hz are shown with increased stimulus amplitudes from 0.05 nA to 0.25 nA.
Figure 1—figure supplement 2
Rate-dependent PRCs are influenced by the dendrite.
PRC obtained in the PC model without its dendrite. (A) The PRC has a different rate adaptation: the peak has a constant width and its amplitude decreases with firing rate. (B) Normalized peak amplitudes at different firing rates. (C) The flat phase has a constant duration.
Figure 2 with 1 supplement
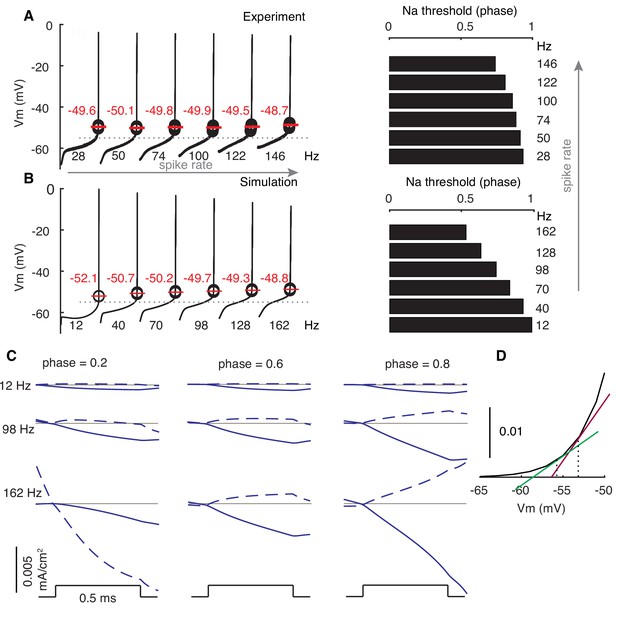
Modulated subthreshold membrane potentials account for the rate adaptation of PRCs.
(A and B) Experimental and simulated voltage trajectories in PCs at different rates. All voltage trajectories are shown from trough to peak within normalized ISIs. The model used (Zang et al., 2018) was not fitted to this specific experimental data. Spike thresholds at different rates are labeled in plots. The Na+ activation threshold is defined as −55 mV (stippled line). Right plots show phase dependence of Na+-activation threshold on firing rates. (C) Stimulus-triggered variations of inward ionic currents (solid) and outward ionic currents (dashed) at different phases and rates. Ionic currents are shifted to 0 (grey line) at the onset of stimulus to compare their relative changes. At phase = 0.2, the outward current is still decreasing due to the inactivation of the large conductance Ca2+-activated K+ current at 162 Hz. (D) Larger slopes of the Na+ activation curve at high membrane potentials.
Figure 2—figure supplement 1
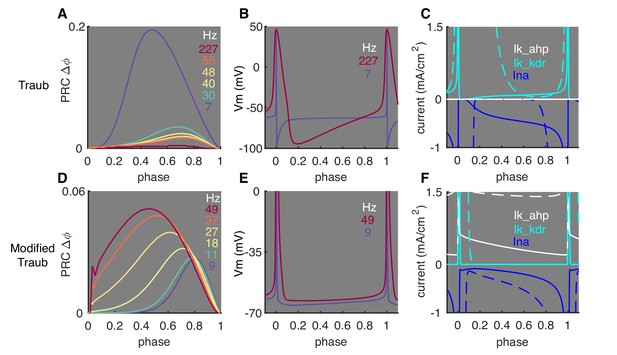
Effect of Subthreshold Membrane Potentials on Shaping PRCs.
We examined whether the critical role of subthreshold membrane potentials in shaping PRC profiles (Figure 2) also applies to other neuron types. A frequently used pyramidal neuron model, the Traub model (Ermentrout et al., 2001) was tested. It shows an opposite rate adaptation of PRCs compared to PCs (A). In the Traub model, responses become smaller and relatively phase-independent at high firing rates. This demonstrates that the normalization used in Equation 1 does not always lead to increasing PRC peak amplitudes for smaller ISIs. These PRC shapes can be explained by significantly lower subthreshold membrane potentials at high rates, compared to PCs, (B). This is due to the accumulation of delayed rectifier K+ current (kdr, C), which has a low activation threshold and large conductance. The lower subthreshold membrane potentials are far below the Na+-activation threshold, making responses to weak stimuli passive at high firing rates. Accordingly, PRCs in the model become smaller and relatively phase-independent at high rates. We minimally modified the Traub model by reducing the conductance of the kdr current, raising its activation threshold and increasing the AHP current (details in Materials and methods) (D-F). With these modifications, subthreshold membrane potentials are significantly elevated at high firing rates lower than 110 Hz. Accordingly, onset-phases of phase-dependent responses shift left and peaks increase at high rates. These simulation results show that spike rate-dependent subthreshold membrane potentials and their effect on nonlinear activation of Na+ currents can be crucial in shaping neuronal PRC profiles in many types of neurons. Surprisingly, when firing rates are higher than 110 Hz, PRCs decrease again, suggesting other undetermined biological mechanisms may be involved in determining the phase responses. (A) Rate adaptation of PRCs in the original Traub model. (B) Lowered ISI membrane potential at high rates. (C) Comparison of ionic currents at low (solid, 7 Hz) and high (dashed, 227 Hz) rates. (D) Rate adaptation of PRCs in the modified Traub model. (E) Elevated ISI membrane potential at high rates. (F) Comparison of ionic currents at low (solid, 9 Hz) and high (dashed, 49 Hz) rates. In (C) and (F), current peaks are truncated to show currents during ISIs. In (E), spike peaks are truncated to show the elevated ISI membrane potential at high rates.
Figure 3
High-frequency oscillations show adaptation to cellular firing rates.
(A) Schematic representation of the network configuration. (B) Example of sampled PC voltage trajectories in the network. (C) Example of population rates in the network (time bin 1 ms). (D) The power spectrum of population rates of the network at different cellular rates and firing irregularity (CV of ISIs). (E) Averaged normalized CCGs at different cellular rates.
Figure 4 with 2 supplements
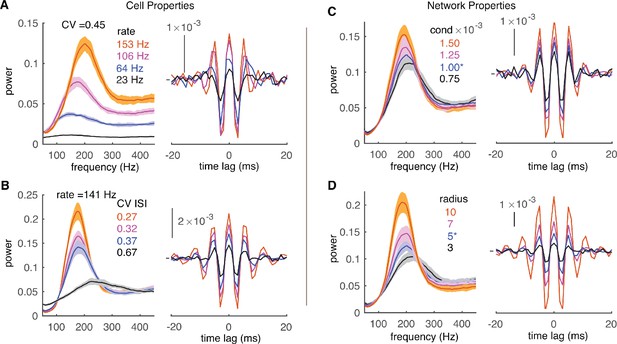
Effect of cell and network properties on high-frequency oscillations.
(A) Low cellular firing rates decorrelate the network output in the forms of reduced peaks of power spectrums (left) and CCGs (right). CV ISI is ~0.45. Synaptic conductance is 1 nS and radius is 5. (B) Irregular spiking (high CV of ISIs) also decorrelates network. The cellular firing rate is ~141 Hz. Same layout and network properties as in A. (C) Small conductance (cond) of inhibitory synapses decorrelates network output. Same layout and network properties as in A with cellular firing rate ~151 Hz and CV ISI ~ 0.45. (D) Short connection radius also decorrelates network output. Same layout and cellular firing properties as C.
Figure 4—figure supplement 1
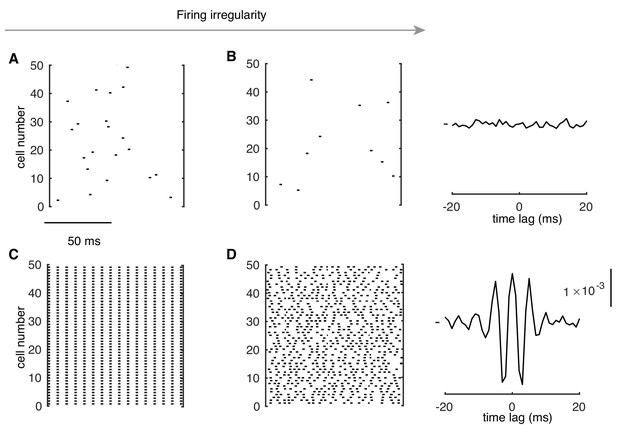
Formation of High-frequency Oscillations at High Rates.
(A and B) Raster plots of random PC spikes when they fire regularly (CV ISI ~ 0.07) and irregularly (CV ISI ~ 0.4) at low rates (here,~2 Hz in the network, but 12 Hz in isolated cells). In the right plot of (B), average CCG is shown. (C) PCs show spike-to-spike synchrony when they fire regularly (CV ISI ~ 0.02) at high rates (154 Hz). (D) PC spikes show high-frequency oscillations when they fire irregularly (CV ISI ~ 0.44) at high rates (153 Hz). The right plot of (D) shows the average CCG with a significant central peak and side peaks.
Figure 4—figure supplement 2
Decreased PRC at high firing rates can weaken oscillations.
(A) PRCs for negative synaptic stimulus when PCs fire at 95 Hz (blue) and 106 Hz (purple) driven by OU process with basal values of synaptic conductance. Reduced PRC at 106 Hz was achieved by 50% of basal synaptic conductance (black). (B) The power spectrum of spike trains with the cellular rate of 95 Hz (blue, basal conductance), 106 Hz (purple, basal conductance) and 113 Hz (black, 50% of basal conductance, firing rate increased to 113 Hz due to the reduced inhibition, with other conditions the same as 106 Hz with basal conductance). In all cases, the CV of ISI is 0.45. The power spectrum at high firing rates gets flatter with lower amplitude when the PRC amplitude is reduced (black trace). (C) The CCGs of spike trains with the same condition as in B. Central and side peaks reduce at high firing rates when the phase response is smaller.
Figure 5
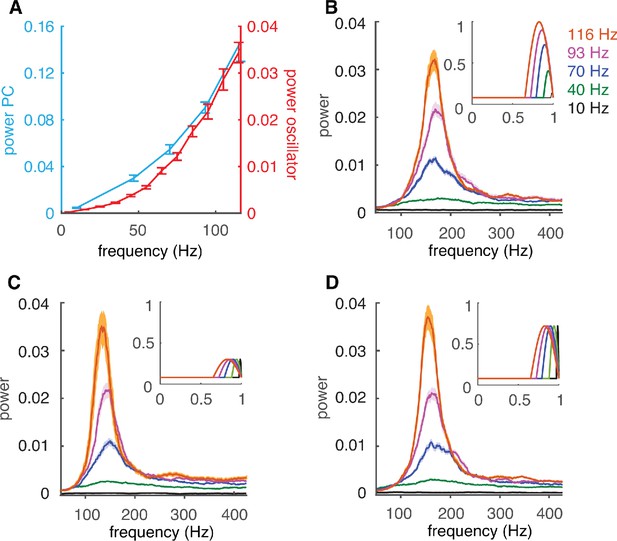
Firing-rate adaptation of high-frequency oscillations is caused by the PRC.
(A) Dependence of peak power of high-frequency oscillations in the complex PC network of Figure 3 (cyan) and in the coupled oscillator network (red) on cellular firing rate. (B) The power spectrum of the coupled oscillator network depends on the cellular firing-rate-specific PRC used as coupling term. Inset: firing-rate-dependent coupling factors Z(θ) used. (C) Same as B but with the peak amplitude of Z(θ) set to that of the peak of 30 Hz firing rate. (D) Same as C for the peak of 70 Hz firing rate.
Figure 6 with 2 supplements
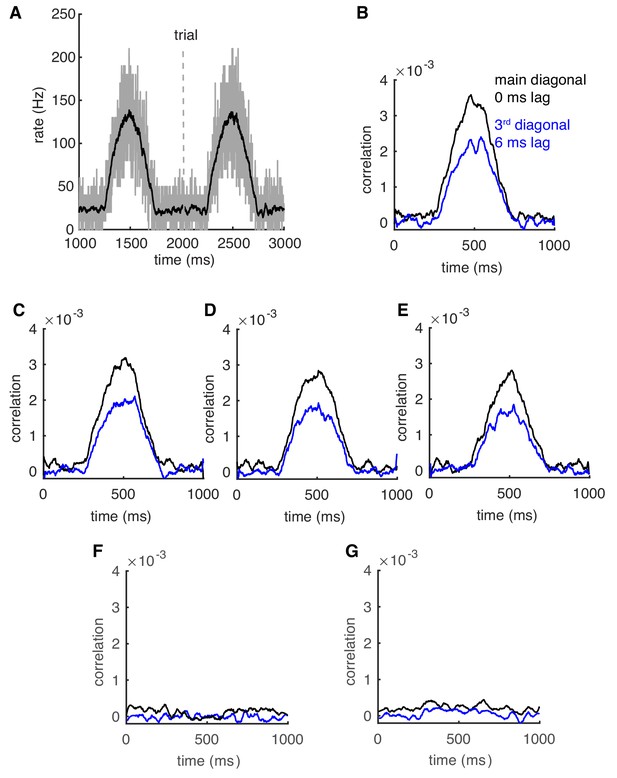
Correlations can be transient and robust to heterogeneous spike rates.
(A) Population spike rates of PCs. (B) The 0 ms- and 6 ms-time lag correlations increase with population rates. (C–E) The rate-dependent correlation is robust to heterogeneous cellular rate changes. From (C) to (E), the number of decreased rate cells increases from 10 to 30. (F) Correlations between decreased-rate neurons in the network (n = 30). (G) Correlations between increased-rate neurons and decreased-rate neurons (n = 30 for each group).
Figure 6—figure supplement 1
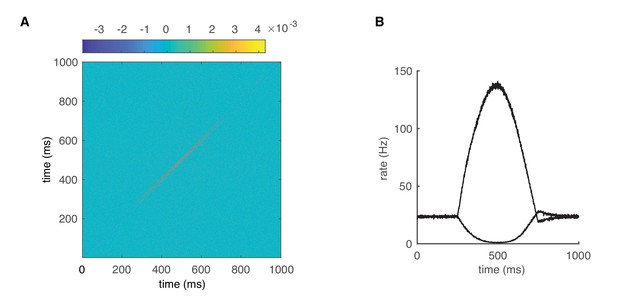
Dynamic correlations of the PC network outputs.
(A) The JPSTH used to produce Figure 6B. (B) Population firing rates of increased-rate cells and decreased-rate cells for Figure 6C–E.
Figure 6—figure supplement 2
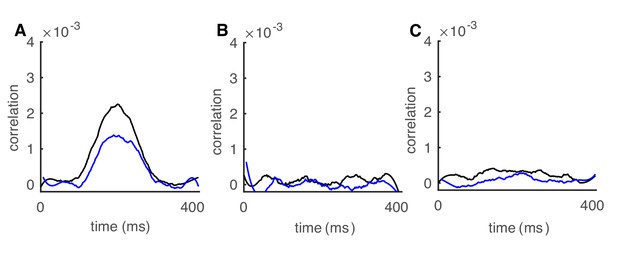
Transient correlations for a 2.5 Hz sine wave.
(A) The 0 ms-time lag (black) and 6 ms-time lag (blue) correlations between increased-rate neurons in the network increase with population rates (n = 100). (B) Correlations between decreased-rate neurons in the network (n = 30). (C) Correlations between increased-rate neurons and decreased-rate neurons (n = 30 for each group).
Additional files
-
Source code 1
Purkinje_PRC_Oscillation_Code.
- https://cdn.elifesciences.org/articles/60692/elife-60692-code1-v1.zip
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/60692/elife-60692-transrepform-v1.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Firing rate-dependent phase responses of Purkinje cells support transient oscillations
eLife 9:e60692.
https://doi.org/10.7554/eLife.60692
