Shape-invariant encoding of dynamic primate facial expressions in human perception
Figures
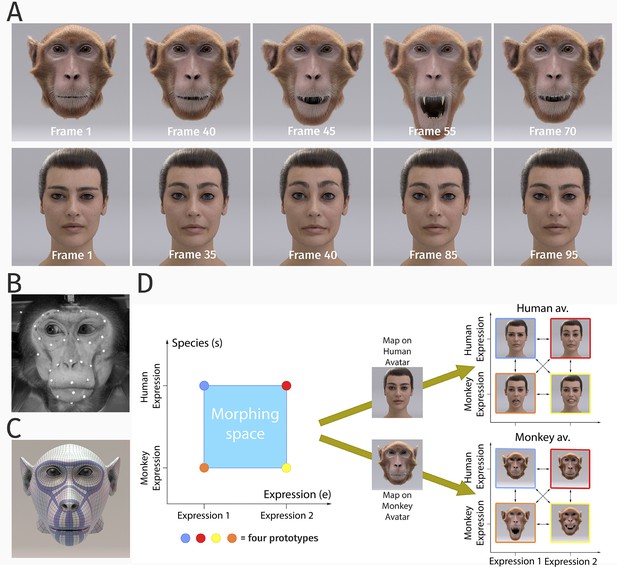
Stimulus generation and paradigm.
(A) Frame sequence of a monkey and a human facial expression. (B) Monkey motion capture with 43 reflecting facial markers. (C) Regularized face mesh, whose deformation is controlled by an embedded elastic ribbon-like control structure that is optimized for animation. (D) Stimulus consisting of 25 motion patterns, spanning up a two-dimensional style space with the dimensions ‘expression’ and ‘species’, generated by interpolation between two expressions (‘anger/threat’ and ‘fear’) and the two species (‘monkey’ and ‘human’). Each motion pattern was used to animate a monkey and a human avatar model.
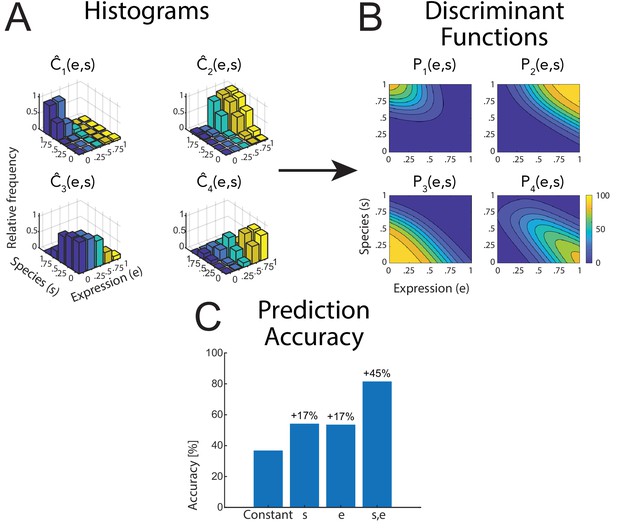
Raw data and statistical analysis.
(A) Histograms of the classification data for the four classes (see text) as functions of the style parameters e and s. Data is shown for the human avatar, front view, using the original motion-captured expressions as prototypes. (B) Fitted discriminant functions using a logistic multinomial regression model (see 'Materials and methods'). Data is shown for the human avatar, front view, using the original motion-captured expressions as prototypes. (C) Prediction accuracy of the multinomial regression models with different numbers of predictors (constant predictor, only style variable e or s, and both of them).
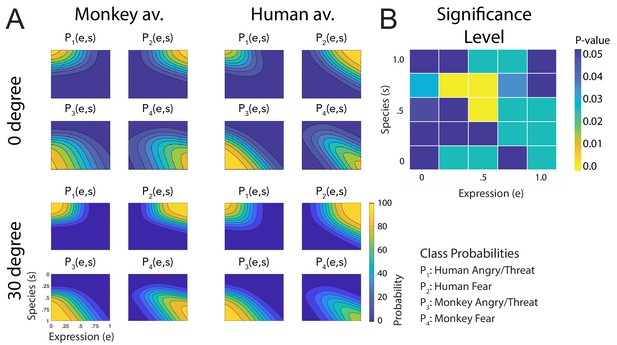
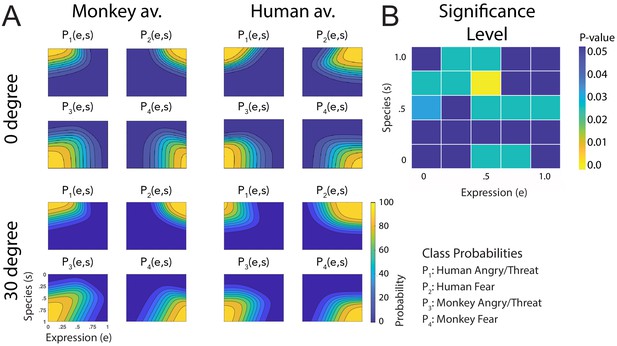
Fitted discriminant functions Pi(e,s) for the original stimuli.
Classes correspond to the four prototype motions, as specified in Figure 1D (i = 1: human-angry, 2: human-fear, 3: monkey-threat, 4: monkey-fear). (A) Results for the stimuli generated using original motion-captured expressions of humans and monkeys as prototypes, for presentation on a monkey and a human avatar. (B) Significance levels (Bonferroni-corrected) of the differences between the multinomially distributed classification responses for the 25 motion patterns, presented on the monkey and human avatar.
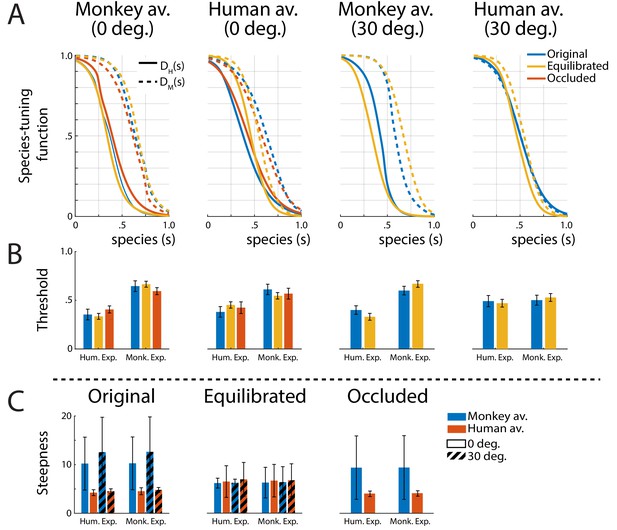
Tuning functions.
(A) Fitted species-tuning functions DH(s) (solid lines) and DM(s) (dashed lines) for the categorization of patterns as monkey vs. human expressions, separately for the two avatar types (human and monkey) and the two view conditions. Different line styles indicate the experiments using original motion-captured motion, stimuli with occluded ears, and the experiment using prototype motions that were equilibrated for the amount of motion/deformation across prototypes. (B) Thresholds of the tuning functions for the three experiments for presentation on the two avatar types and the two view angles. (C) Steepness of the tuning functions at the threshold points for the experiments with and without equilibration of the prototype motions, and with occlusion of the ears.
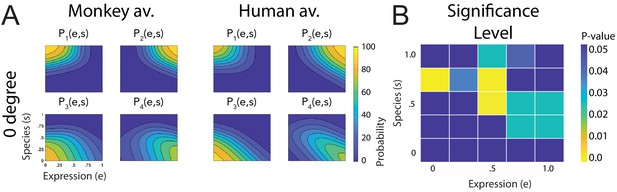
Fitted discriminant functions Pi(e,s) for the condition with occlusions of the ears.
Classes correspond to the four prototype motions, as specified in Figure 1D (i = 1: human-angry, 2: human-fear, 3: monkey-threat, 4: monkey-fear). (A) Results for the stimuli generated using original motion-captured expressions of humans and monkeys as prototypes but with occluded ears, for presentation on a monkey and a human avatar (only using the front view). (B) Significance levels (Bonferroni-corrected) of the differences between the multinomially distributed classification responses for the 25 motion patterns, presented on the monkey and human avatar.
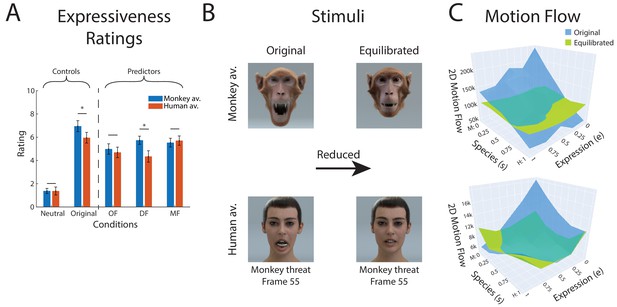
Equilibration of low-level expressive information.
(A) Mean perceived expressivity ratings for stimulus sets that were equilibrated using different types of measures for the amount of expressive low-level information: OF: optic flow computed with an optic flow algorithm; DF: shape difference compared to the neutral face (measured by the 2D distance in polygon vertex space); MF: two-dimensional motion of the polygons on the surface of the face. In addition, the ratings for a static neutral face are shown as reference point for the rating (neutral). (B) Extreme frames of the monkey threat prototype before and after equilibration using the MF measure (C) 2D polygon motion flow (MF) computed for the 25 stimuli in our expression style space for the monkey avatar for the front view (similar results were obtained for the other stimulus types).
Fitted discriminant functions Pi(e,s) for the experiment with equilibration of expressive information.
Classes correspond to the four prototype motions, as specified in Figure 1D (i = 1: human-angry, 2: human-fear, 3: monkey-threat, 4: monkey-fear). (A) Results for the stimuli set derived from prototype motions that were equilibrated with respect to the amount of local motion/deformation information, for presentation on a monkey and a human avatar. (B) Significance levels (Bonferroni-corrected) of the differences between the multinomially distributed classification responses for the 25 motion patterns, presented on the monkey and human avatar.
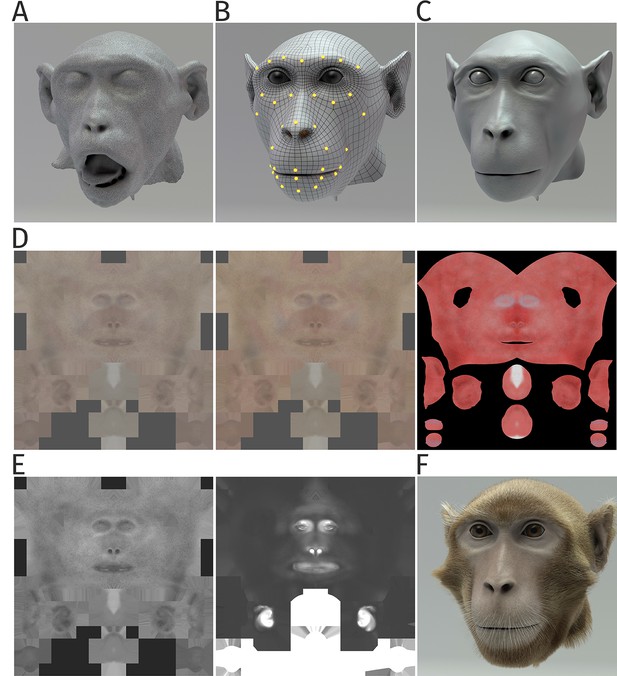
Details of generation of the monkey head model.
(A) Irregular surface mesh resulting from the magnetic resonance scan of a monkey head. (B) Face mesh, the deformation of which is following control points specified by motion-captured markers. (C) Surface with a high polygon number derived from the mesh in (B), applying displacement texture maps, including high-frequency details such as pores and wrinkles. (D) Skin texture maps modeling the epidermal layer (left), the dermal layer (middle), and the subdermal layer (right panel). (E) Specularity textures modeling the reflection properties of the skin; overall specularity (left) and the map specifying oily vs. wet appearance (right panel). (F) Complete monkey face model, including the modeling of fur and whiskers.
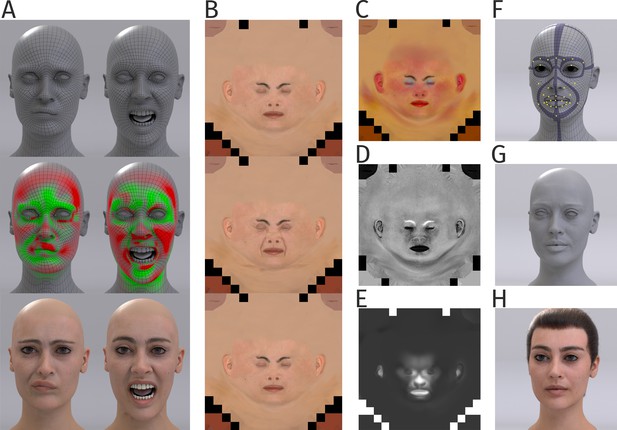
Details of generation of the human head model.
(A) Human face mesh and deformations by a blendshape approach, in which face poses are driven by the 43 control points (top panel). Tension map algorithm computes compression (green) and stretching (red) of mesh during animation (middle panel). Corresponding texture maps were blended (bottom panel). (B) Examples of diffuse texture maps (top panel), with additional maps for stretching (middle panel) and compression (bottom panel). (C) Subsurface color map modeling the color variations by light scattering and reflection by the skin. (D) Specular map modeling the specularity of the skin. (E) Wetness map modeling the degree of wetness vs. oilyness of the skin. (F) Regularized basic mesh with embedded muscle-like ribbon structures (violet) for animation. Yellow points indicate the control points defined by the motion capture markers. (G) Mesh with additional high-frequency details. (H) Final human avatar including hair animation.
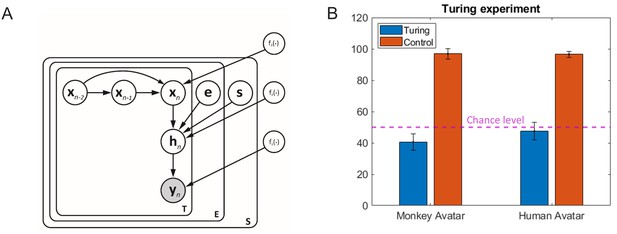
Motion morphing algorithm and additional results.
(A) Graphical model showing the generative model underlying our motion morphing technique. The hierarchical Bayesian model has three layers, reducing subsequently the dimensionality of the motion data yn. The top layer models the trajectory in latent space using a Gaussian process dynamical model (GPDM). The vectors e and s are additional style vectors that encode the expression type and the species type. They are binomially distributed. Plate notation indicates the replication of model components for the encoding of the temporal sequence, and the different styles. Nonlinear functions are realized as samples from Gaussian processes with appropriately chosen kernels (for details, see text). (B) Results from Turing test experiment. Accuracy for the distinction between animations with original motion capture data and trajectories generated by our motion morphing algorithm is close to chance level (dashed line), opposed to the accuracy for the detection of small motion artifacts in control stimuli, which was almost one for both avatar types.
Tables
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Software, algorithm | Custom-written software written in C# | This study | https://hih-git.neurologie.uni-tuebingen.de/ntaubert/FacialExpressions (copy archived at swh:1:rev:6d041a0a0cc7055618f85891b85d76e0e7f80eed; Taubert, 2021) | |
| Software, algorithm | C3Dserver | Website | https://www.c3dserver.com | |
| Software, algorithm | Visual C++ Redistributable for Visual Studio 2012 Update4 × 86 and x64 | Website | https://www.microsoft.com/en-US/download/details.aspx?id=30679 | |
| Software, algorithm | AssimpNet | Website | https://www.nuget.org/packages/AssimpNet | |
| Software, algorithm | Autodesk Maya 2018 | Website | https://www.autodesk.com/education/free-software/maya | |
| Software, algorithm | MATLAB 2019b | Website | https://www.mathworks.com/products/matlab.html | |
| Software, algorithm | Psychophysics toolbox 3.0.15 | Website | http://psychtoolbox.org/ | |
| Software, algorithm | R 3.6 | Website | https://www.r-project.org/ | |
| Other | Training data for interpolation algorithm | This study | https://hih-git.neurologie.uni-tuebingen.de/ntaubert/FacialExpressions/tree/master/Data/MonkeyHumanFaceExpression | |
| Other | Stimuli for experiments | This study | https://hih-git.neurologie.uni-tuebingen.de/ntaubert/FacialExpressions/tree/master/Stimuli |
Model comparison.
Results of the accuracy and the Bayesian Information Criterion (BIC) for the different logistic multinomial regression models for the stimuli derived from the original motion (no occlusions) for the monkey and the human avatar. The models included the following predictors: Model 1: constant; Model 2: constant, s; Model 3: constant, e; Model 4: constant, s, e; Model 5: constant, s, e, product s⋅e; Model 5: constant, s, e, Optic Flow.
| Model comparison | ||||||||
|---|---|---|---|---|---|---|---|---|
| Monkey front view | Model | Accuracy [%] | Accuracy increase [%] | BIC | Parameters | df | χ2 | p |
| Model 1 | 38.29 | 7487 | 33 | |||||
| Model 2 | 57.86 | 19,56 (relative to Model 1) | 5076 | 36 | 3 | 2411 | <0,0001 | |
| Model 3 | 49.49 | 11,2 (relative to Model 1) | 6125 | 36 | 3 | 1362 | <0,0001 | |
| Model 4 | 77.53 | 19,67 (relative to Model 2) | 3586 | 39 | 3 | 1490 | <0,0001 | |
| Model 5 | 77.53 | 0 (relative to Model 4) | 3598 | 42 | 3 | 11.997 | <0.0074 | |
| Model 6 | 77.42 | −0,11 (relative to Model 4) | 3580 | 42 | 3 | 5.675 | 0.129 | |
| Human front view | ||||||||
| Model 1 | 36.84 | 7481 | 33 | |||||
| Model 2 | 54.22 | 17,38 (relative to Model 1) | 5541 | 36 | 3 | 1940 | <0,0001 | |
| Model 3 | 53.56 | 16,72 (relative to Model 1) | 5847 | 36 | 3 | 1633 | <0,0001 | |
| Model 4 | 81.56 | 27,35 (relative to Model 2) | 3420 | 39 | 3 | 2120 | <0,0001 | |
| Model 5 | 81.35 | −0,22 (relative to Model 4) | 3309 | 42 | 3 | 112 | <0,0001 | |
| Model 6 | 81.38 | −0,18 (relative to Model 4) | 3389 | 42 | 3 | 31.66 | <0,0001 | |
| Monkey 30-degree | ||||||||
| Model 1 | 35.32 | 6913 | 33 | |||||
| Model 2 | 57.40 | 22,08 (relative to Model 1) | 4314 | 36 | 3 | 2622 | <0,0001 | |
| Model 3 | 49.36 | 14,04 (relative to Model 1) | 5179 | 36 | 3 | 1757 | <0,0001 | |
| Model 4 | 84.04 | 26,64 (relative to Model 2) | 2359 | 39 | 3 | 1977 | <0,0001 | |
| Model 5 | 84.88 | 0,84 (relative to Model 4) | 2335 | 42 | 3 | 48 | <0,0001 | |
| Model 6 | 84.08 | 0,04 (relative to Model 4) | 2331 | 42 | 3 | 28 | <0,0001 | |
| Human 30-degree | ||||||||
| Model 1 | 37.40 | 6819 | 33 | |||||
| Model 2 | 55.72 | 18,32 (relative to Model 1) | 4843 | 36 | 3 | 1975 | <0,0001 | |
| Model 3 | 54.36 | 16,96 (relative to Model 1) | 5217 | 36 | 3 | 1602 | <0,0001 | |
| Model 4 | 81.32 | 25,6 (relative to Model 2) | 2910 | 39 | 3 | 1956 | <0,0001 | |
| Model 5 | 82.88 | 1,56 (relative to Model 4) | 2809 | 42 | 3 | 101 | <0,0001 | |
| Model 6 | 81.92 | 0,6 (relative to Model 4) | 2890 | 42 | 3 | 19 | 0.0002 |
Parameters of the Bayesian motion morphing algorithm.
The observation matrix Y is formed by N samples of dimension D, where N results from S * E trails with T time steps. The dimensions M and Q of the latent variables were manually chosen. The integers S and E specify the number of species and expressions (two in our case).
| Parameters of motion morphing algorithm | ||
|---|---|---|
| Parameters | Description | Value |
| D | Data dimension | 208 |
| M | First layer dimension | 6 |
| Q | Second layer dimension | 2 |
| T | Number of samples per trial | 150 |
| S | Number of species | 2 |
| E | Number of expressions | two or 3 |
| N | Number of all samples | T * S * E |
| Hyper parameters (learned) | Size | |
| Inverse width of kernel | 1 | |
| Inverse width of kernel | 1 | |
| Inverse width for non-linear part one of kernel | 1 | |
| Inverse width for non-linear part two of kernel | 1 | |
| Precision absorbed from noise term | 1 | |
| Variance for non-linear part of | 1 | |
| Variance for linear part of | 1 | |
| Variance for non-linear part of | 1 | |
| Variance for linear part of | 1 | |
| Variance for non-linear part of | 1 | |
| Variance for linear part one of | 1 | |
| Variance for linear part two of | 1 | |
| Variables | Size | |
| Y | Data | N x D |
| H | Latent variable of first layer | N x M |
| X | Latent variable of second layer | N x Q |
| Style variable vector for monkey species | S x 1 | |
| Style variable vector for human species | S x 1 | |
| Style variable vector for expression one | E x 1 | |
| Style variable vector for expression two | E x 1 | |
Detailed results of the two-way ANOVAs.
ANOVA for the threshold: two-way mixed model with expression type as within-subject factor and the stimulus type as between-subject factor for both the monkey and the human avatar. Steepness: two-way ANOVA with avatar type and expression factor for each stimulus motion type (original, occluded, and equilibrated). The mean square is defined as Mean Square = Sum of Square/df; df = degree of freedom.
| ANOVAs | ||||||
|---|---|---|---|---|---|---|
| Threshold | Monkey avatar | Sum of square | df | Mean square | F | p |
| Stimulus type | 0,00 | 2 | 0,00 | 0,00 | 0999 | |
| Expression type | 1,20 | 1 | 1,20 | 188,83 | 0000 | |
| Stimulus * Expression | 0,06 | 2 | 0,03 | 4,51 | 0015 | |
| Error | 0,42 | 60 | 0,01 | |||
| Total | 1,72 | 65 | ||||
| Human avatar | ||||||
| Stimulus type | 0,00 | 2 | 0,00 | 0,01 | 0993 | |
| Expression type | 0,40 | 1 | 0,40 | 46,37 | 0000 | |
| Stimulus * Expression | 0,05 | 2 | 0,03 | 3,15 | 0049 | |
| Error | 0,57 | 60 | 0,01 | |||
| Total | 1,02 | 65 | ||||
| Steepness | Original motion stimulus | |||||
| Avatar type | 376,68 | 1 | 376,68 | 6,3 | 0016 | |
| Expression type | 0,36 | 1 | 0,36 | 0,01 | 0939 | |
| Avatar * Expression | 0,16 | 1 | 0,16 | 0 | 0959 | |
| Error | 2391,21 | 40 | 59,78 | |||
| Total | 2768,41 | 43 | ||||
| Occluded motion stimulus | ||||||
| Avatar type | 286,17 | 1 | 286,17 | 3,33 | 0076 | |
| Expression type | 0,02 | 1 | 0,02 | 0 | 0988 | |
| Avatar * Expression | 0,00 | 1 | 0,00 | 0 | 0995 | |
| Error | 3094,54 | 36 | 85,96 | |||
| Total | 3380,73 | 39 | ||||
| Equilibrated motion stimulus | ||||||
| Avatar type | 1,57 | 1 | 1,57 | 0,4 | 0533 | |
| Expression type | 0,25 | 1 | 0,25 | 0,06 | 0803 | |
| Avatar * Expression | 0,02 | 1 | 0,02 | 0 | 0945 | |
| Error | 174,76 | 44 | 3,97 | |||
| Total | 176,60 | 47 | ||||





