Bayesian inference of population prevalence
- School of Psychology and Neuroscience, University of Glasgow, United Kingdom
- Department of Statistics, University of Glasgow, United Kingdom
Figures
Figure 1
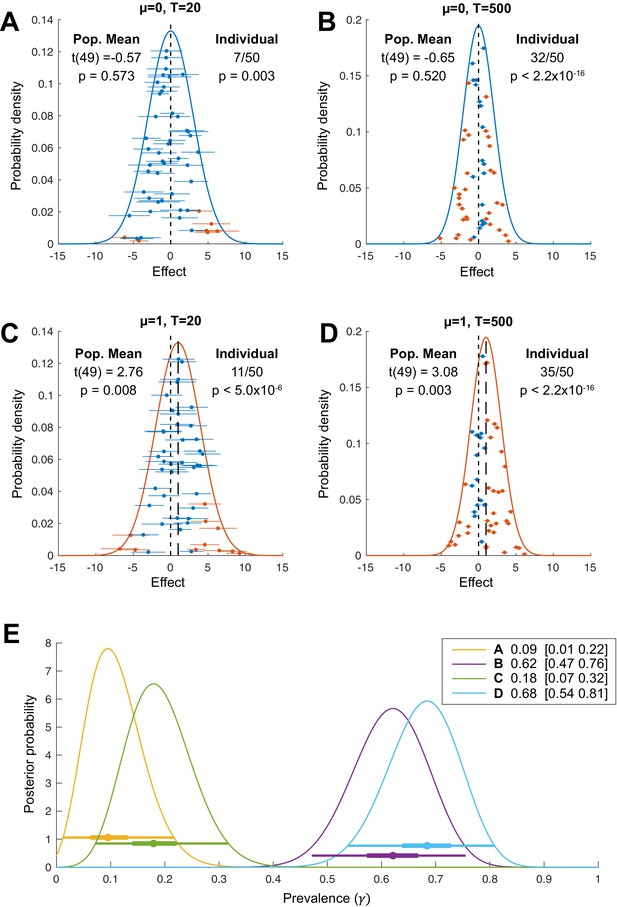
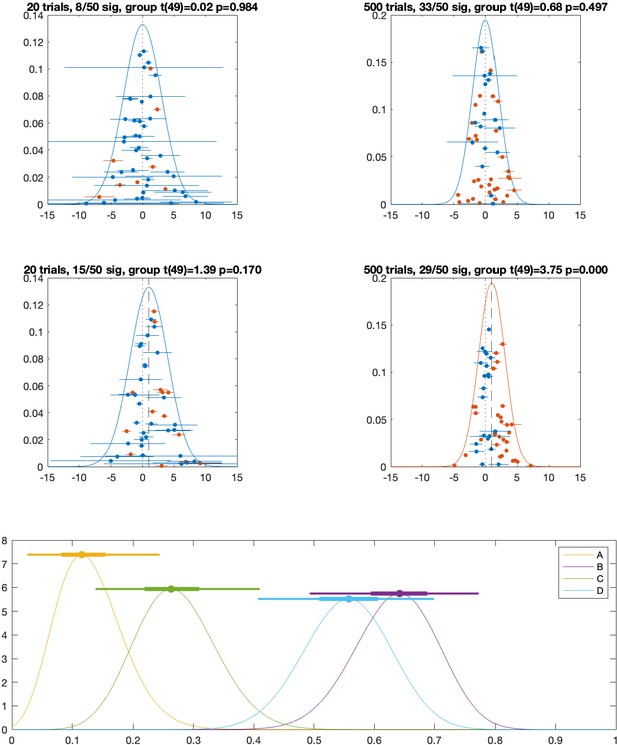
Population vs individual inference.
For each simulation, we sample individual participant mean effects from a normal distribution with population mean (A, B) ; (C, D) and between-participant standard deviation . Within each participant, trials (A, C) ; (B, D) are drawn from a normal distribution with the participant-specific mean and a common within-participant standard deviation (Baker et al., 2020). Orange and blue indicate, respectively, exceeding or not exceeding a p=0.05 threshold for a t-test at the population level (on the within-participant means, population normal density curves) or at the individual participant level (individual sample means ± s.e.m.). (E): Bayesian posterior distributions of population prevalence of true positive results for the four simulated data sets (A–D). Circles show Bayesian maximum a posteriori (MAP) estimates. Thick and thin horizontal lines indicate 50% and 96% highest posterior density intervals (HPDIs), respectively. MAP (96% HPDI) values are shown in the legend.
Figure 2
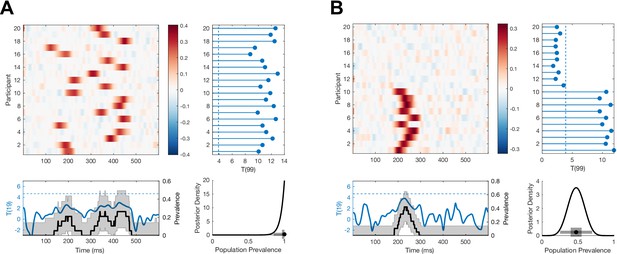
Simulated examples where Bayesian prevalence and second-level t-tests diverge.
EEG traces are simulated for 100 trials from 20 participants as white noise, , with an additive Gaussian activation ( = 20 ms) with amplitudes drawn from a uniform distribution on [0 0.6]. For each simulation, mean traces are shown per participant (upper-left panel). A second-level t-test is performed at each time point separately (blue curve, lower-left panel), dashed line shows the p=0.05 threshold, Bonferroni corrected over time points. A within-participant t-test is performed at each time point and for each participant separately (right-hand panel); the blue points show the maximum T-statistic over time for each participant, and the dashed line shows the p=0.05 Bonferroni corrected threshold. Lower-right panel shows posterior distribution of population prevalence for an effect in the analysis window. Black curves (lower-left panel) show the prevalence posterior at each time point (black line maximum a posteriori [MAP], shaded area 96% highest posterior density interval [HPDI]). (A) An effect is simulated in all participants, with a peak time uniformly distributed in the range 100–400 ms. (B) An effect is simulated in 10 participants, with a peak time uniformly distributed in the range 200–275 ms.
Figure 3
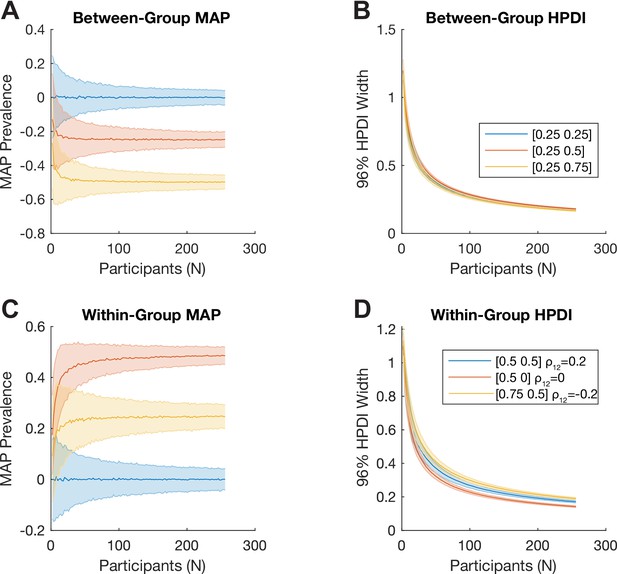
Bayesian inference of difference of prevalence.
(A, B) We consider two independent groups of participants with population prevalence of true positives of [25%, 25%] (blue), [25%, 50%] (red), and [25%, 75%] (yellow). We show how (A) the Bayesian MAP estimate and (B) 96% highest posterior density interval (HPDI) width of the estimated between-group prevalence difference scale with the number of participants. (C, D) We consider two tests applied to the same sample of participants. Here, each simulation is parameterised by the population prevalence of true positives for the two tests, , as well as , the correlation between the (binary) test results across the population. We show this for [50%, 50%] with (blue), [50%, 0%] with (red), and [75%, 50%] with (yellow). We show how (C) the Bayesian maximum a posteriori (MAP) estimate and (D) 96% HPDI width of the estimated within-group prevalence difference scale with the number of participants.
Figure 4
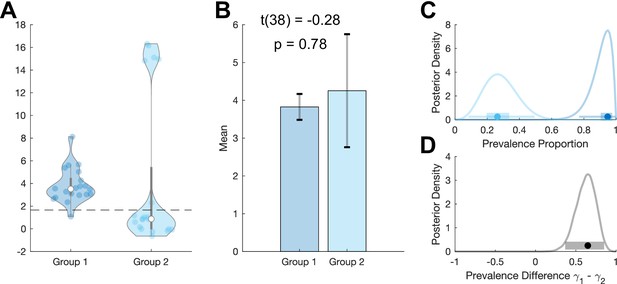
Example where between-group prevalence diverges from two-sample t-test.
We simulate standard hierarchical Gaussian data for two groups of 20 participants, , , per group. (A) Group 1 participants are drawn from a single population Gaussian distribution with . Group 2 participants are drawn from two Gaussian distributions. 75% of participants are drawn from and 25% of participants are drawn from . Dashed line shows the p=0.05 within-participant threshold (one-sample t-test). The means of these two groups are not significantly different (B), but they have very different prevalence posteriors (C). The posterior distribution for the difference in prevalence shows the higher prevalence in group 1: 0.61 [0.36 0.85] (MAP [96% HPDI]) (D). MAP: maximum a posteriori; HDPI: highest posterior density interval.
Figure 5
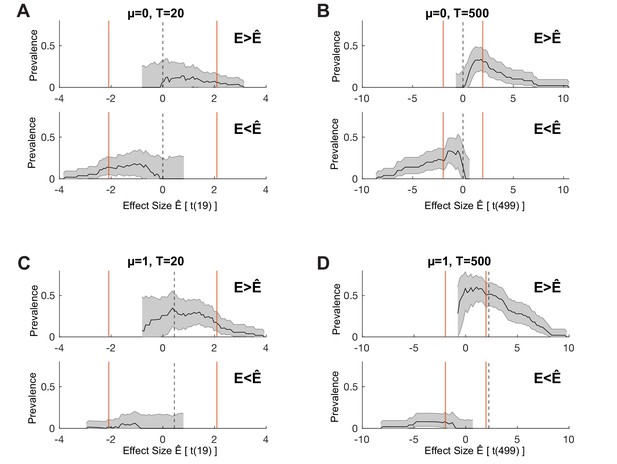
One-sided prevalence as a function of effect size.
We consider the same simulated systems shown in Figure 1, showing both right-tailed () and left-tailed () prevalence as a function of effect size. Orange lines show the effect size corresponding to the two-sided within-participant test, as used in Figure 1. Dashed lines show the effect size corresponding to the ground truth of the simulation. (A,B) , (C,D) . (A,C) T = 20 trials, (B,D) T = 500 trials. Black line shows maximum a posteriori (MAP), shaded region shows 96% highest posterior density interval (HPDI).
Figure 6
Examples of different effect size prevalence curves with similar p=0.05 prevalence.
EEG traces are simulated for 100 trials from 20 participants as white noise [ ] with an additive Gaussian activation ( = 20 ms) with amplitudes drawn from a uniform distribution. For each simulation, mean traces are shown per participant (upper-left panel). A within-participant t-test is performed at each time point and for each participant separately (right-hand panel); the blue points show the maximum T-statistic over time for each participant, and the dashed line shows the p=0.05 Bonferroni corrected threshold. Lower-right panel shows posterior distribution of population prevalence for an effect in the analysis window. Black curves (lower-left panel) show the prevalence (maximum a posteriori [MAP], shaded area 96% highest posterior density interval [HPDI]) as a function of effect size threshold. (A) A weak early effect is simulated in all participants (peak time uniformly distributed 100–150 ms). (B) In addition to the same early effect, a stronger, longer ( = 40 ms), and more temporally variable later effect is simulated in 10 participants (peak times 250–450 ms). (C) Early events are simulated with the same timing as (A), but each participant has a different maximum amplitude (participants ordered by effect size). All three simulations have similar prevalence of p=0.05 effects, but show differing patterns of prevalence over different effect size thresholds.
Figure 7
Characterisation of Bayesian prevalence inference.
(A–C) We consider the binomial model of within-participant testing for three ground truth population proportions: 25%, 50%, and 75% (blue, orange, yellow, respectively). We show how (A) the Bayesian maximum a posteriori (MAP) estimate, (B) 95% Bayesian lower bound, and (C) 96% highest posterior density interval (HPDI) width scale with the number of participants. Lines show theoretical expectation, coloured regions show ±1 s.d. (D–F) We consider the population model from Figure 1C and D (). (D) Power contours for the population inference using a t-test (Baker et al., 2020). Colour scale shows statistical power (probability of rejecting the null hypothesis). (E) Contours of average Bayesian MAP estimate for . Colour scale shows MAP prevalence proportion. (F) Contours of average 95% Bayesian lower bound for . Colour scale shows lower bound prevalence. From the prevalence perspective, the number of trials obtained per participant has a larger effect on the resulting population inference than does the number of participants.
Author response image 1
Same as Figure 1 from manuscript, but within-participant standard deviation is sampled from a log-normal distribution with mean log(10) and standard deviation log(3).
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Bayesian inference of population prevalence
eLife 10:e62461.
https://doi.org/10.7554/eLife.62461
