A modular approach to integrating multiple data sources into real-time clinical prediction for pediatric diarrhea
Figures

Temperature in The Gambia over study period with (blue) trend line from LOESS (locally estimated scatterplot smoothing).
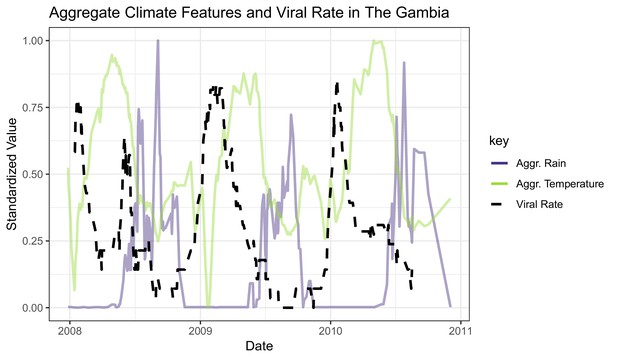
The black line represents a 2-week rolling average of daily viral etiology rates over time.
The purple and green lines represent the prior 2-week average of daily rain and temperature averages.
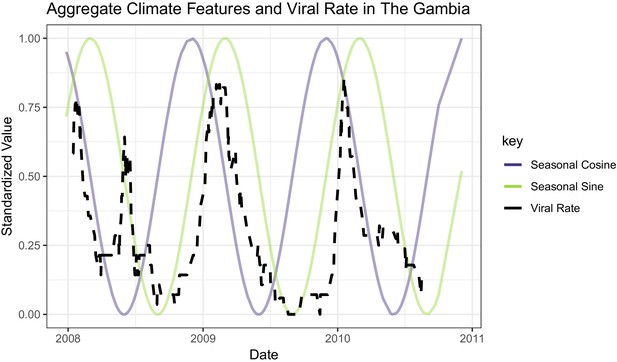
The black line represents a 2-week rolling average of daily viral etiology rates over time.
The purple and green lines represent the prior 2-week average of daily rain and temperature averages.
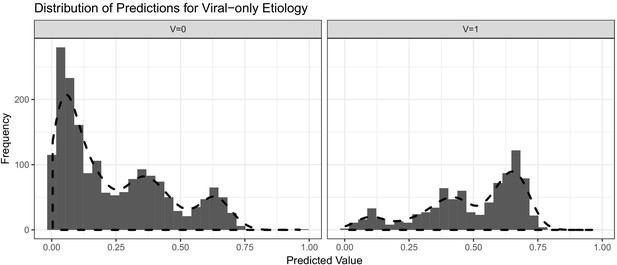
Histograms with overlaid estimated kernel densities (dashed lines) of predicted values obtained from logistic regression on patient training data.
The left graph represent other known etiologies and the right graph represent viral etiologies. The dashed lines do not represent standardized density heights so the heights for V = 0 and V = 1 should not be compared from this graph.
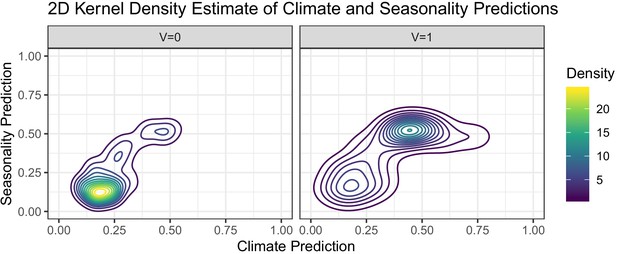
Contour plots of two-dimensional kernel densities of predicted values obtained from logistic regression on GEMS climate and seasonality data in Mali.
The right graph represents viral etiologies and the left graph represents other known etiologies.
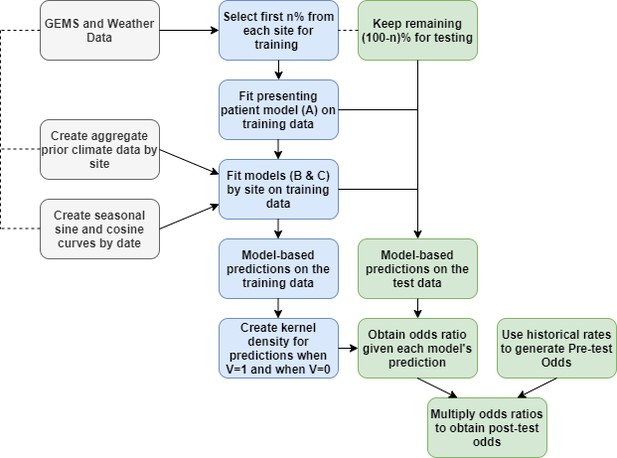
The steps for fitting prediction models and calculating the post-test odds for within rolling-origin-recalibration evaluation.
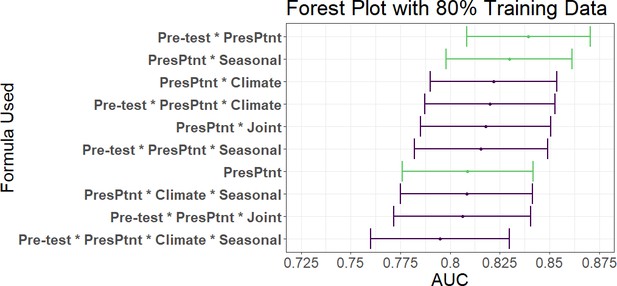
AUC’s and confidence intervals for post-test odds used in the 80% training and 20% testing iteration.
'PresPtnt' refers to the predictive model using the presenting patient’s information. 'Pre-test' refers tot he use of pre-test odds based on prior patients’ predictive models. 'Climate' refers to the predictive model using aggregate local weather data. 'Seasonal' refers to the predictive model based on seasonal sine and cosine curves. 'Joint' refers to the two-dimensional kernel density estimate from the Seasonal and Climate predictive models.
-
Figure 4—source data 1
AUC’s and confidence intervals for post-test odds used in the 80%training and 20%testing iteration.
- https://cdn.elifesciences.org/articles/63009/elife-63009-fig4-data1-v1.csv
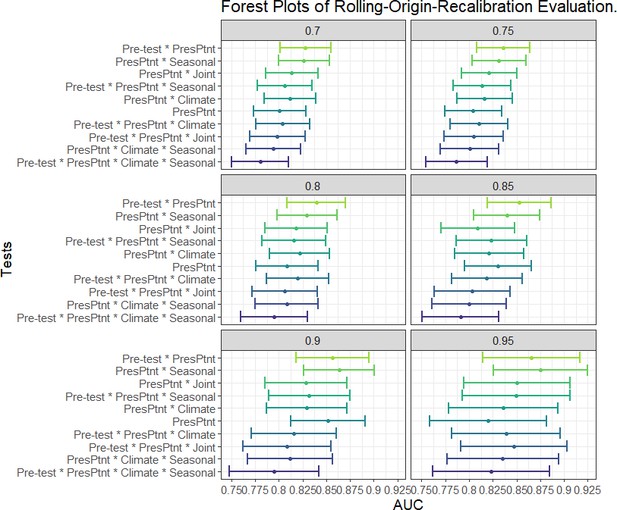
AUC’s and confidence intervals for tests used in within rolling-origin-recalibration evaluation.
Individual plot titles show the proportion of data used in training.
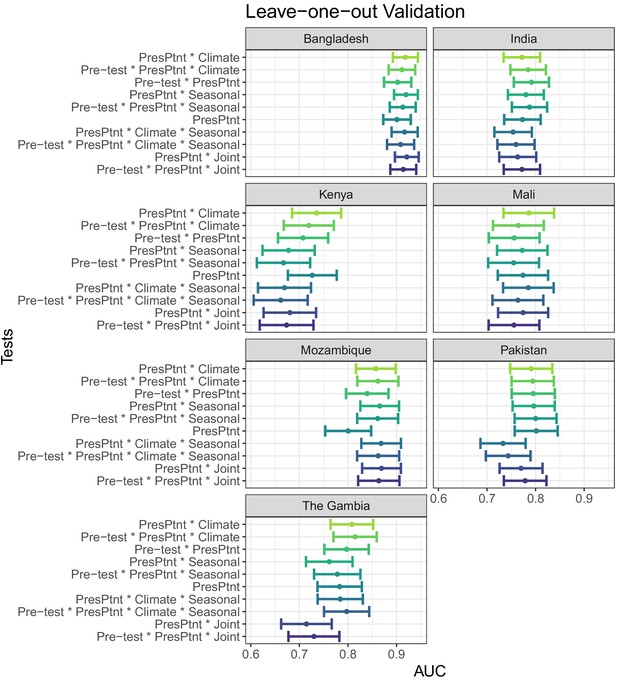
AUC’s and confidence intervals for tests used in the leave-one-site-out evaluation.
Pre-test refers to the use of prior patient predictions. Individual plot titles show the site left out of training.
Tables
Rank of variable importance by average reduction in the mean squared prediction error of the response using Random Forest regression.
Greyed rows are variables that would be accessible for providers in LMICs at the time of presentation. Table 1 is reproduced from Brintz et al., 2020, PLoS Negl Trop Dis., published under the Creative Commons Attribution 4.0 International Public License (CC BY 4.0; https://creativecommons.org/licenses/by/4.0/).
| Viral etiology | |
|---|---|
| Variable name | Variance reduction |
| Age | 51.6 |
| Season | 29.0 |
| Blood in stool | 26.1 |
| Height-for-age Z-score | 24.7 |
| Vomiting | 23.0 |
| Breastfeeding | 22.0 |
| Mid-upper arm circumference | 20.9 |
| Respiratory rate | 18.5 |
| Wealth index | 18.3 |
| Body Temperature | 16.7 |
AUC results by site using 80% of data for training and 20% of data for testing of the top two models.
PresPtnt refers to the model fit using presenting patient information.
| Country | Test set size | Formula | AUC (95% CI) |
|---|---|---|---|
| Kenya | 79 | Pre-test * PresPtnt | 0.65 (0.53–0.77) |
| PresPtnt * Seasonal | 0.66 (0.54–0.78) | ||
| PresPtnt | 0.63 (0.51–0.75) | ||
| Mali | 88 | Pre-test * PresPtnt | 0.74 (0.61–0.86) |
| PresPtnt * Seasonal | 0.78 (0.66–0.89) | ||
| PresPtnt | 0.75 (0.62–0.87) | ||
| Pakistan | 108 | Pre-test * PresPtnt | 0.81 (0.72–0.89) |
| PresPtnt * Seasonal | 0.8 (0.72–0.88) | ||
| PresPtnt | 0.81 (0.73–0.89) | ||
| India | 119 | Pre-test * PresPtnt | 0.84 (0.76–0.91) |
| PresPtnt * Seasonal | 0.85 (0.78–0.92) | ||
| PresPtnt | 0.81 (0.74–0.89) | ||
| The Gambia | 80 | Pre-test * PresPtnt | 0.89 (0.82–0.96) |
| PresPtnt * Seasonal | 0.87 (0.79–0.94) | ||
| PresPtnt | 0.78 (0.67–0.88) | ||
| Mozambique | 66 | Pre-test * PresPtnt | 0.88 (0.79–0.97) |
| PresPtnt * Seasonal | 0.9 (0.82–0.98) | ||
| PresPtnt | 0.77 (0.66–0.89) | ||
| Bangladesh | 141 | Pre-test * PresPtnt | 0.91 (0.82–1) |
| PresPtnt * Seasonal | 0.93 (0.88–0.99) | ||
| PresPtnt | 0.95 (0.92–0.99) |
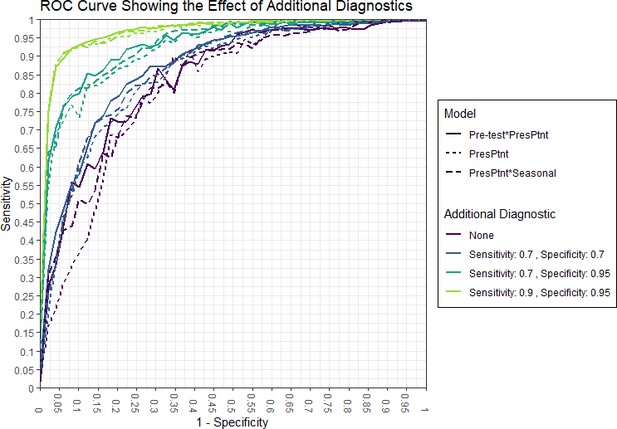
AUC and 95% confidence intervals from 80% training set after adding an additional point-of-care diagnostic test with specified sensitivities (Se.) and specificities (Sp.) to the current patient test and pre-test odds.
Additionally, + and - refer to our model indicating a true positive or false positive, respectively, based on the threshold for each model which achieves a 0.90 or 0.95 specificity. Only patients who were prescribed/given antibiotics are included in the count.
| Specificity=0.90 | Specificity=0.95 | |||||
|---|---|---|---|---|---|---|
| Model | Addl. diag. (Se.,Sp.) | Auc (95% CI) | True + | False + | True + | False + |
| Pre-test * PresPtnt | None | 0.839 (0.809–0.869) | 88 | 29 | 60 | 16 |
| (0.7, 0.7) | 0.876 (0.849–0.902) | 102 | 31 | 78 | 16 | |
| (0.7, 0.95) | 0.933 (0.914–0.952) | 132 | 31 | 123 | 16 | |
| (0.9, 0.95) | 0.972 (0.960–0.984) | 154 | 34 | 147 | 18 | |
| PresPtnt * Seasonal | None | 0.830 (0.798–0.861) | 70 | 25 | 54 | 11 |
| (0.7, 0.7) | 0.870 (0.842–0.897) | 101 | 27 | 68 | 14 | |
| (0.7, 0.95) | 0.931 (0.912–0.951) | 130 | 27 | 121 | 16 | |
| (0.9, 0.95) | 0.971 (0.959–0.984) | 154 | 30 | 149 | 18 | |
| PresPtnt | None | 0.809 (0.776–0.842) | 66 | 31 | 41 | 15 |
| (0.7, 0.7) | 0.857 (0.827–0.886) | 98 | 33 | 68 | 16 | |
| (0.7, 0.95) | 0.925 (0.904–0.946) | 129 | 33 | 117 | 18 | |
| (0.9, 0.95) | 0.968 (0.955–0.981) | 153 | 34 | 149 | 18 | |
-
Table 3—source data 1
Frequency table of pathogens in which the post-test odds formulation with varying specifity (Sp.) chosen have false positives.
- https://cdn.elifesciences.org/articles/63009/elife-63009-table3-data1-v1.docx
Average AUC’s from one-dimensional and two-dimensional kernel density estimates (KDE) when the post-test odds conditional independence assumption is broken.
The table shows the factor () used to simulate induced conditional dependence between two covariates and their average conditional correlation. Additionally, it shows the average AUC resulting from a post-test odds model where a one-dimensional kernel density estimate (conditional independence assumed) is generated for each covariate, and a post-test odds model where a two-dimensional joint kernel density estimate is derived for the two covariates.
| AUC | |||
|---|---|---|---|
| 1D-KDE | 2D-KDE | ||
| -2.000 | −0.894 | 0.725 | 0.830 |
| -1.000 | −0.709 | 0.758 | 0.828 |
| -0.500 | −0.446 | 0.824 | 0.838 |
| 0.000 | 0.002 | 0.838 | 0.836 |
| 0.500 | 0.448 | 0.836 | 0.836 |
| 1.000 | 0.708 | 0.831 | 0.840 |
| 2.000 | 0.894 | 0.810 | 0.836 |