Slowing the body slows down time perception
- University of California, Davis, United States
- George Mason University, United States
Figures
Figure 1 with 2 supplements
Hypothesis and design of Experiment 1.
(A) Potential pathways in which movement (f) could influence timing. The first possibility is that f specifically alters the sensory layer, in which a stimulus presented for an amount of time (t) is …
Figure 1—figure supplement 1
Additional effects for categorization and reproduction tasks.
(A) Data from the temporal categorization task of Experiment 1. Left panel: Mean chronometric functions of reaction time against tested durations for all four viscosity levels. Inner Left panel: …
Figure 1—figure supplement 2
Individual differences in movement parameters for categorization and reproduction tasks.
(A) Individual movement parameters for the temporal categorization task of Experiment 1. Left panel: Average values of Movement Distance and Total Force for each individual subject (each unique …
Figure 2
Viscosity shifts time responses.
(A) Results from Experiment 1 (Temporal Categorization). Left panel: psychometric curves fit to response proportions for a representative subject exhibiting a rightward shift with increasing …
Figure 3
Movement speed does not change viscosity effects, but does influence precision.
(a) Mean bisection points and (b) coefficients of variation for participant trials divided into high and low movement via a median split. Viscosity shifted the bisection point across both movement …
Figure 4 with 2 supplements
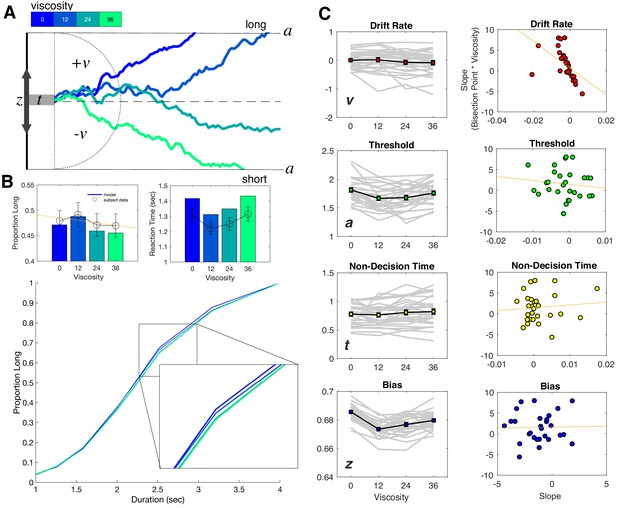
Drift diffusion modeling of categorization performance and viscosity.
(A) Example Viscosity DDM model, in which evidence is accumulated to one of two decision bounds (‘long’ and ‘short’), separated by a. Evidence accumulation drifts at particular rate (v) that can be …
Figure 4—figure supplement 1
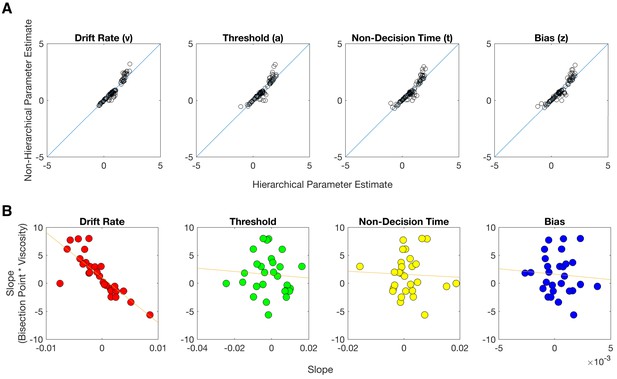
Comparison of hierarchical and non-hierarchical fits for Experiment 1.
(A) Scatterplots of parameter estimates for all four parameters from the Viscosity Model fit using hierarchical or non-hierarchical methods. Blue lines represent the identity. Parameter estimates …
Figure 4—figure supplement 2
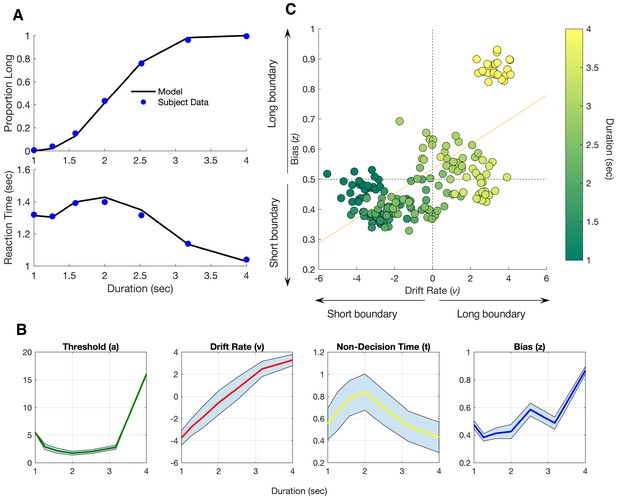
Parameters and simulations of the Duration Model for Experiment 1.
(A) Posterior predictive checks of simulated Duration Model against average subject data. Top and bottom panels display psychometric and chronometric curves, respectively. (B) Average Parameter …
Figure 5
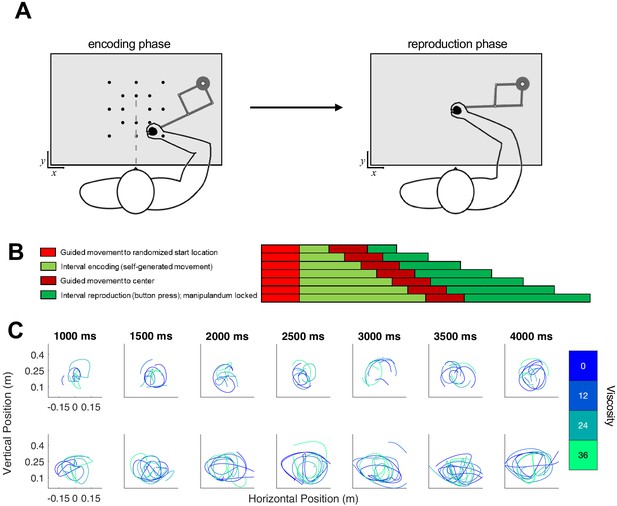
Task schematic of Experiment 2.
(A) Participants began each trial at a randomized start location and were required to initiate movement in order for the test duration to play (encoding phase). Unlike Experiment 1, the desired …
Figure 6
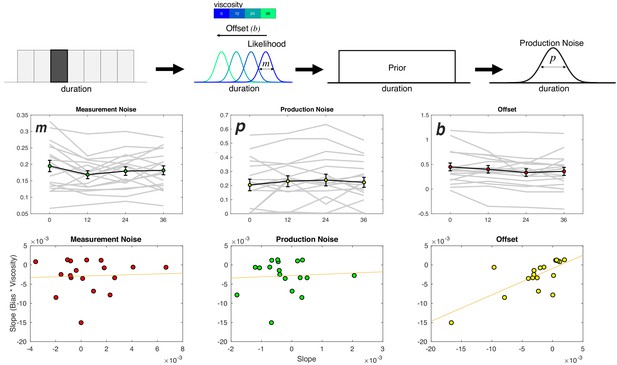
Viscosity shifts time reproduction.
Top: Bayesian Observer Model. On a given trial, a presented duration is drawn from a likelihood distribution with scalar variance leading to a measurement estimate (m) that is shifted by an offset …
Figure 7
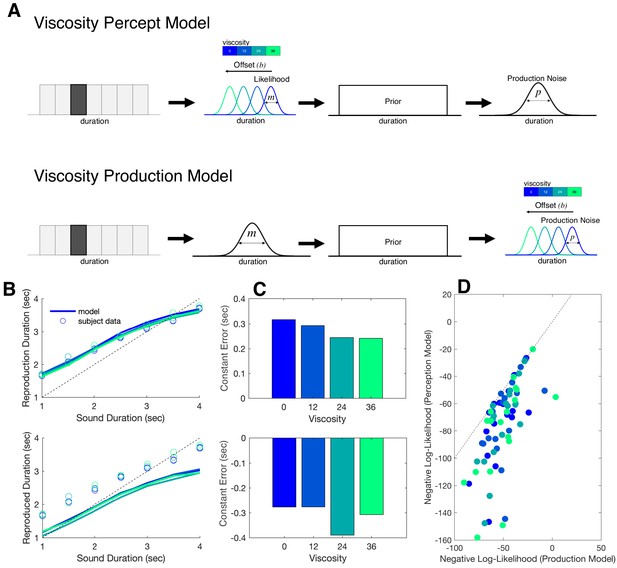
Bayesian observer model of reproduction performance and viscosity.
(A) Schematics for separate Bayesian models, in which the offset term could occur at either measurement level (Perception Model) or the production level (Production Model). (B) Predictive checks for …
Author response image 1
Tables
Table 1
Correlation coefficients and Fisher Z comparisons between fitted parameters and behavioral effects.
| Experiment 1 - Correlation with Viscosity Effect | Experiment 2 - Correlation with Viscosity Effect | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| drift (v) | threshold (a) | starting point (z) | non decision time (t) | offset (b) | production (p) | measurement (m) | |||
| Pearson | *0.5132 | 0.1211 | 0.0196 | 0.0926 | Pearson | *0.7332 | 0.0626 | 0.0509 | |
| Spearman | *0.7865 | 0.168 | 0.0252 | 0.0733 | Spearman | *0.709 | -0.1022 | -0.0299 | |
| Fisher Z compare Pearson with drift | -3.491 | -1.588 | -2.424 | Fisher Z compare Pearson with drift | 2.508 | 2.545 | |||
| Fisher Z compare Spearman with drift | -5.312 | -3.242 | -3.886 | Fisher Z compare Spearman with drift | 2.711 | 2.263 | |||
