Asymmetric random walks reveal that the chemotaxis network modulates flagellar rotational bias in Helicobacter pylori
- Artie McFerrin Department of Chemical Engineering, Texas A&M University, United States
- Department of Biomedical Engineering, Texas A&M University, College Station, TX 77840, United States
- Department of Translational Medical Sciences, Texas A&M University, United States
Figures
Figure 1
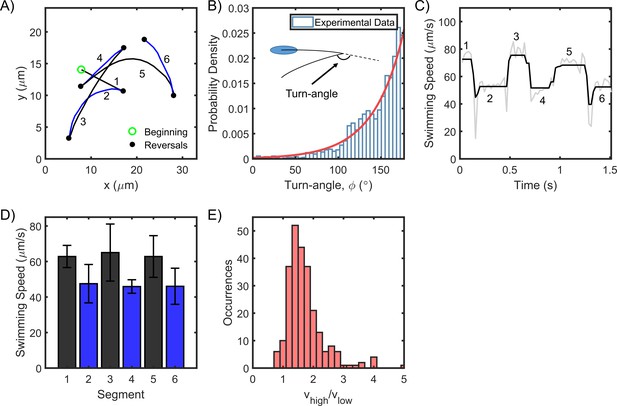
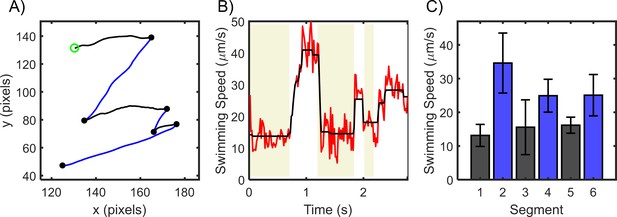
H. pylori swim forward and backward at different speeds.
(A) Representative swimming trace of a single bacterium. Each reversal is represented by a filled circle. The beginning of the trajectory is denoted by an open circle. Uninterrupted swimming between two reversals was labeled as a segment and the segments were numbered chronologically. (B) The turn angles were exponentially distributed (n = 1653 samples); reversals mostly caused the cells to retrace their movements. (C) The swimming speed for a single cell over 1.5 s is indicated. The speeds alternated between high and low values with each reversal. Raw data is indicated in gray; filtered data is indicated in black. (D) The mean speed for each segment is indicated chronologically. Standard deviations are indicated. (E) The mean speed for the high (low) mode for each cell was calculated by averaging over all its high- (low-) speed segments. The distribution of the ratios of the high and low mean speeds for each cell is indicated. The mean ratio was 1.5 ± 0.4 (n = 250 cells).
-
Figure 1—source data 1
Swimming asymmetry.
- https://cdn.elifesciences.org/articles/63936/elife-63936-fig1-data1-v1.xlsx
Figure 2
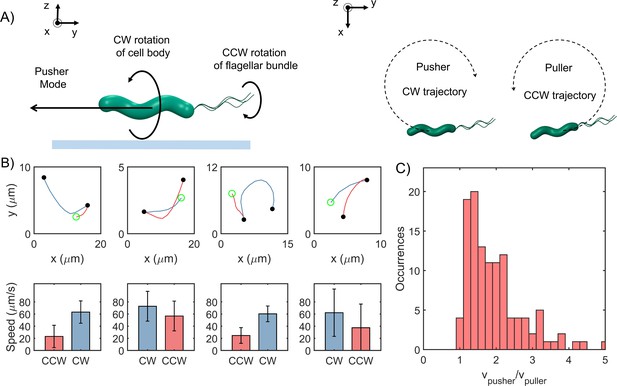
Cells swim faster in the pusher mode.
(A) The viscous drag on the bottom of the cell body and the flagellar filament is higher near an underlying surface (indicated by the blue line in the left panel). The drag is lower on the top half of the body and filament. This difference in drag causes a lateral thrust on the cell, giving rise to circular trajectories: CW trajectory in the pusher mode and CCW trajectory in the puller mode (right panel). (B) Top row: Blue segments indicate CW trajectories; red segments indicate CCW trajectories. Filled circles indicate reversals; open circle indicates the beginning of the trajectory. Bottom row: The corresponding mean speeds and standard deviations are indicated for the two trajectories: CW tracks were always faster than CCW tracks. (C) The distribution of the ratio of the speeds along the pusher and puller modes is indicated (n = 116 cells). The mean ratio = 1.6 ± 0.5.
-
Figure 2—source data 1
Hydrodynamic interactions.
- https://cdn.elifesciences.org/articles/63936/elife-63936-fig2-data1-v1.xlsx
Figure 3
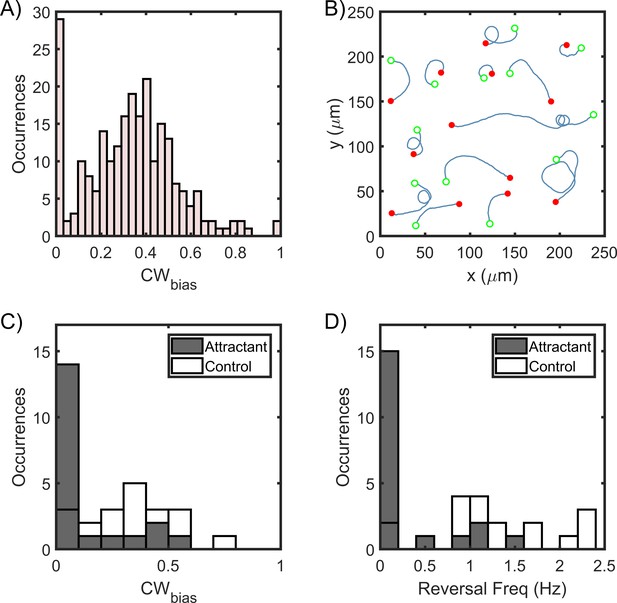
Asymmetric swimming speeds enable quantification of chemotaxis output.
(A) CWbias was determined at 37°C in the absence of chemical stimulants. Cell trajectories with durations of 1 s or more were considered for calculation. The distribution was obtained from n = 240 cells. A Gaussian fit to the switching population (n = 212 cells) yielded CWbias = 0.35 ± 0.23 (mean ± standard deviation). (B) Single-cell trajectories of a ΔcheY mutant are indicated. Cells swam in CW-only trajectories, which indicate CCW flagellar rotation. Open green circles denote the start of a trajectory; filled red circles denote the end. The trajectories were spatially displaced to group them for the purpose of illustration and truncated to show the direction of rotation. Full trajectories and additional cells are included in Appendix 1—figure 1. (C) The post-stimulus CWbias was monitored for ~30–60 s immediately following exposure to 20 mM urea (n = 20 cells); 14 cells swam exclusively in the pusher mode during the period of observation and displayed CW-only trajectories near surfaces. In the control case, cells were exposed to the buffer-only. The average post-stimulus CWbias was 0.31 ± 0.04 (mean ± standard error, n = 20 cells). The difference in the mean bias for the attractant and the control cases was significant (p-value<0.001). (D) The post-stimulus reversal frequency for cells treated with urea was 0.23 ± 0.09; those treated with the buffer had an average reversal frequency of 1.4 ± 0.04. The difference in the mean frequency for the attractant and the control cases was significant (p-value<0.001).
-
Figure 3—source data 1
CWbias modulation.
- https://cdn.elifesciences.org/articles/63936/elife-63936-fig3-data1-v1.xlsx
Figure 4
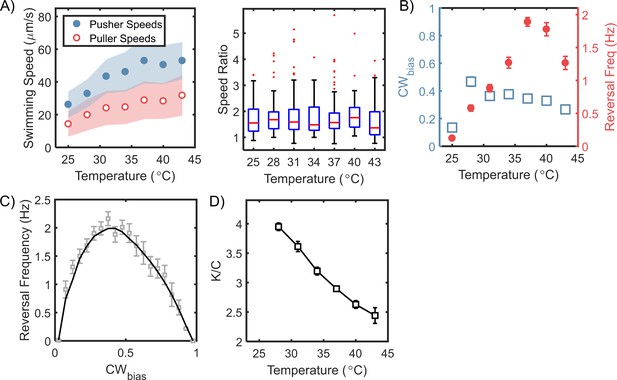
Steady-state chemotactic output is independent of temperature.
(A) Left: Swimming speeds for each mode are plotted (mean ± standard deviation) for different temperatures. The speeds increased with temperature till 37°C, after which they plateaued. The shaded regions indicate standard deviation. Right: The ratios of the pusher and puller speeds are independent of the temperatures, as indicated. A red horizontal line indicates the median ratio at each temperature, and the bottom and top borders of the encompassing box indicate the 25th and 75th percentiles. The extended lines span 99.3% of the data and the dots indicate outliers. (B) Mean CWbias (open squares) and mean reversal frequencies (filled circles) are plotted over a range of temperatures. The switching frequency was at a maximum at the physiological temperature (37°C) and decreased at higher and lower temperatures. The CWbias increased with the temperature and plateaued above 30°C. The mean values are indicated with standard error. Each data-point was averaged over n ≥ 80 cells. (C) The relationship between reversal frequency and CWbias is indicated. The values were obtained from the combined datasets over the entire range of temperatures that we studied (n = 972 cells). The CWbias was binned (bin size = 0.05), and the mean reversal frequency for each bin was estimated. The mean and standard errors are indicated in grey. The black curve is a guide to the eye. (D) The estimated ratio of the CheY-P dissociation constant () and the intracellular CheY-P concentrations () is indicated as a function of the temperature. The ratios were calculated from the data in (B) following a previous approach (Turner et al., 1999). The number of binding sites for CheY-P in H. pylori ~ 43 was estimated from the relative sizes of the flagellar C-ring (see Appendix 2 and Qin et al., 2017). The ratio of the dissociation constants for the CCW and the CW motor conformations was assumed to be similar to that in E. coli (~ 4.7 from Fukuoka et al., 2014).
-
Figure 4—source data 1
Thermal response.
- https://cdn.elifesciences.org/articles/63936/elife-63936-fig4-data1-v1.xlsx
Figure 5
Asymmetric random walks in a run-reversing bacterium.
(A) Experimentally observed wait-time intervals for runs and reversals obey a Gamma distribution (n = 515 samples): the shape and scale parameters were k = 2.92 ± 0.06 and θ = 0.11 ± 0.00, respectively. (B) Cell swims at μm/s in the puller (slower) mode, and at μm/s in the pusher (faster) mode. The symmetric case is described by a = 0, where the run and reverse speeds are equal. Cell alignment is described by the unit vector e. (C) The diffusion coefficients predicted from equation 1 are indicated as a function of the asymmetry in speeds (blue curve). An alternate model that assumes exponentially distributed wait-time intervals in asymmetric swimmers under predicted the diffusivity, as shown by the dotted curve (Theves et al., 2013). Symbols indicate coefficients calculated from simulation runs (see Appendix 5). The parameters were based on experimental measurements: mean wait-time = 0.3 s, α = 0.86, and 25 μm/s. = 0.02 s−1 from (Großmann et al., 2016). Diffusion coefficients have been non-dimensionalized with ( Lovely and Dahlquist, 1975), where is the mean reversal frequency at the physiological temperature (Figure 4B). (D) Diffusion coefficients were calculated from simulations of cell motility in the absence of a stimulus over a range of a and CWbias values (see Appendix 5 for details). The diffusion coefficients were normalized with . The sum of the mean wait-times (CW and CCW) was fixed at 0.35 s. (E) Predicted diffusivity is indicated over a range of typical reversal frequencies. Here, α = 0.86 and = 0.02 s−1.
-
Figure 5—source data 1
Stochastic model.
- https://cdn.elifesciences.org/articles/63936/elife-63936-fig5-data1-v1.xlsx
Figure 6
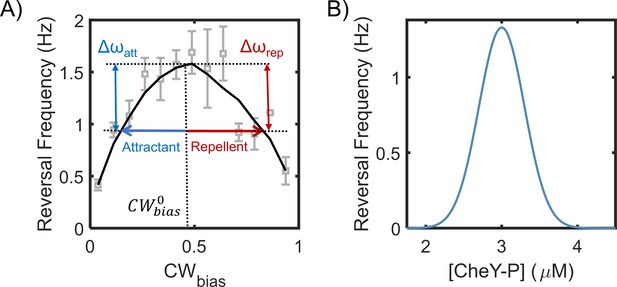
Motor reversal (switching) frequencies versus CWbias and CheY-P.
(A) The dependence of motor reversal frequencies in E. coli on the CWbias is unimodal (Montrone et al., 1998), similar to H. pylori (Figure 4B). The symbols indicate experimental data from Montrone et al., 1998. The black curve is a guide to eye. The blue and red arrows indicate the effect of attractants and repellents on the CWbias, respectively. The corresponding changes in the reversal frequency are similar (Δωatt ~ Δωrep). (B) The dependence of switching frequency on CheY-P levels is also unimodal in E. coli (Cluzel et al., 2000). Thus, an attractant as well as a repellent can induce a drop in the frequency.
Appendix 1—figure 1
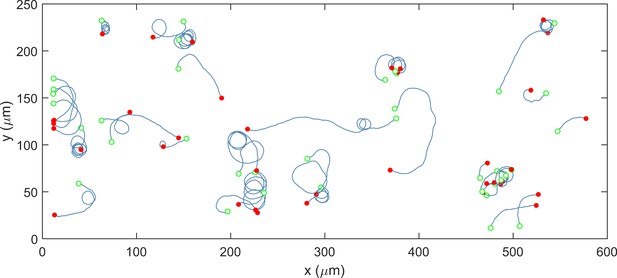
Single-cell trajectories of a H. pylori PMSS1 ΔcheY mutant are indicated.
The cells swam in clockwise-only trajectories as shown: open green circles denote the start of a trajectory; filled red circles denote the end. This behavior was observed for n > 150 cells; here we show 38 cells.
Appendix 2—figure 1
The switching rates were estimated from the CWbias and the reversal frequencies reported in Figure 4B (main text).
The maximum and values were attained at 37°C (2.75 ± 0.20 s−1 and 1.43 ± 0.08 s−1). The standard error is indicated.
Appendix 3—figure 1
Variation in wait-times in the pusher and puller modes with CWbias.
Each point on the plot is calculated by averaging over the number of samples noted above the point.
Appendix 3—figure 2
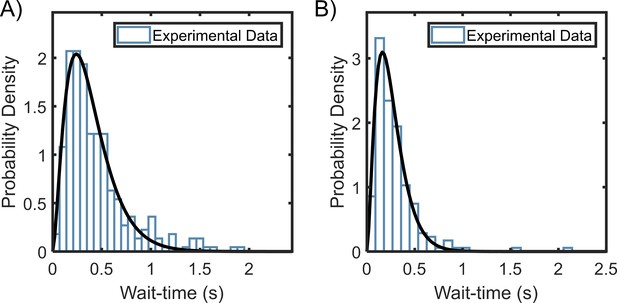
Wait-time distributions for (A) pusher mode (n = 322 segments) and (B) puller mode (n = 196 segments).
Gamma-fits reveal that the mean ± variance in wait-times for the pusher mode is 0.38 ± 0.06 and that for the puller mode is 0.26 ± 0.02.
Appendix 4—figure 1
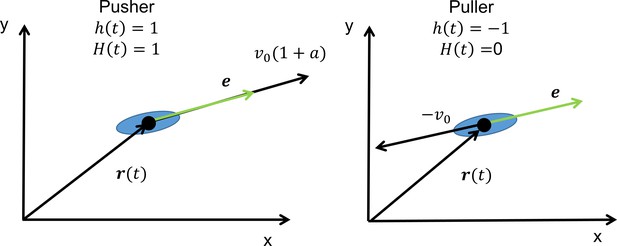
Cell alignment and position are defined by the vectors e and r.
Function alternates between −1 and 1 with each reversal. The Heaviside function, , describes the magnitudes of the two swimming modes with the asymmetry parameter .
Appendix 5—figure 1
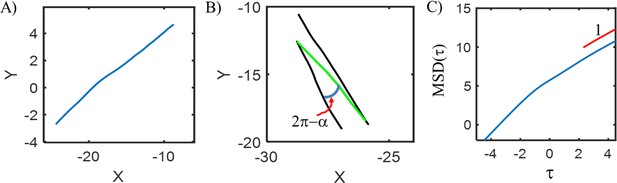
Simulation results.
(A) A representative cell trajectory as it engages in a simulated run. The total run interval, , was split into 71 batches. The trajectory is not a straight-line owing to Brownian motion. (B) Two simulated reversals are indicated. Black and green segments indicate pusher () and puller () modes, respectively. (C) Bacterial movements became purely diffusive over long times (~ 100 s) as indicated by the linear dependence of MSD on lag time (log-log plot). The value of the diffusion coefficient was calculated at these long times.
Appendix 6—figure 1
Cells of H. pylori exhibit asymmetry ~200 μm away from surfaces.
(A) Trajectory of a representative cell is shown, where the segment-color changes upon each reversal. Beginning of the trajectory is denoted by a green circle, reversals are denoted by black circles. (B) Quantitatively determined speeds of the same cell. The shaded regions indicate alternating swimming modes. (C) Average speed for each segment along with the standard deviation is indicated in a chronological manner.
Videos
Video 1
A representative cell exhibits reversals within the field of view (movie has been slowed 3X).
Tables
Table 1
Speed asymmetry across different bacterial species.
| Species | Swimming Speed Ratio | Motor Speed Ratio | Reference |
|---|---|---|---|
| H. pylori | 1.5 | - | This work |
| P. putida | 2 | - | Theves et al., 2013 |
| V. alginolyticus | 1.5 | - | Magariyama et al., 2005 |
| Burkholderia spp. | 3.9 | - | Kinosita et al., 2018 |
| Vibrio fischeri | 3.4 | - | Kinosita et al., 2018 |
| C. crescentus | 1 | ~2 | Lele et al., 2016; Liu et al., 2014 |
| E. coli | ~1.3 | 1.3 | Yuan et al., 2010; Lele and Berg, 2015 |
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Cell line (H. pylori) | PMSS1 | Ottemann Lab | Arnold et al., 2011 | |
| Chemical compound, drug | Brucella Broth | Millipore Sigma | B3051 | |
| Chemical compound, drug | Columbia agar | Thermo Scientific Oxoid | CM0331 | |
| Chemical compound, drug | Defibrinated Horse Blood | Hemostat Laboratories | DHB100 | |
| Chemical compound, drug | Fetal Bovine Serum | Gibco | 10438 | |
| Chemical compound, drug | Polymixin-B sulfate | Alfa Aesar | J6307403 | |
| Chemical compound, drug | Vancomycin hydrochloride | Sigma Aldrich | V1130 | |
| Chemical compound, drug | β-Cyclodextrin | Sigma Aldrich | C4767 | |
| Chemical compound, drug | Urea | Fisher Scientific | BP169 |
Appendix 4—table 1
Value of for different possibilities.
For odd or even number of reversals occurring between time and , corresponding cases of initial and final values for state function h and Heaviside function H are considered. Substituting and values in (3), G is calculated for each case.
| Number of reversals | |||||
|---|---|---|---|---|---|
| Even | 1 | 1 | 1 | 1 | |
| Even | −1 | −1 | 0 | 0 | 1 |
| Odd | 1 | −1 | 1 | 0 | |
| Odd | −1 | 1 | 0 | 1 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Asymmetric random walks reveal that the chemotaxis network modulates flagellar rotational bias in Helicobacter pylori
eLife 10:e63936.
https://doi.org/10.7554/eLife.63936
