Muscle-specific economy of force generation and efficiency of work production during human running
- Humboldt-Universität zu Berlin, Department of Training and Movement Sciences, Germany
- Berlin School of Movement Science, Humboldt-Universität zu Berlin, Germany
Figures
Figure 1
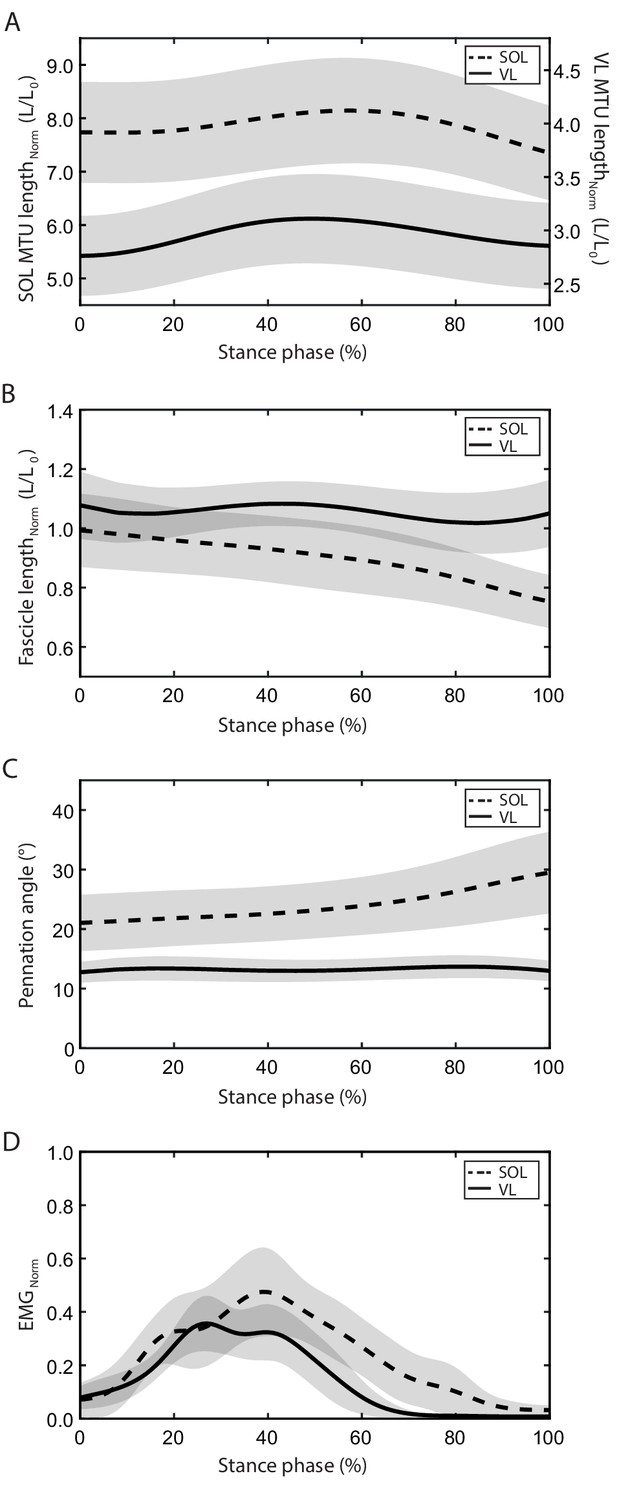
Soleus (SOL, n = 19) and vastus lateralis (VL, n = 14) muscle-tendon unit (MTU) length (A) and muscle fascicle length (normalized to optimal fascicle length L0, B), pennation angle (C), and electromyographic (EMG) activity (normalized to a maximum voluntary isometric contraction, D) during the stance phase of running (mean ± SD).
-
Figure 1—source data 1
Numerical data represented in the graph 1.
- https://cdn.elifesciences.org/articles/67182/elife-67182-fig1-data1-v1.xlsx
Figure 2
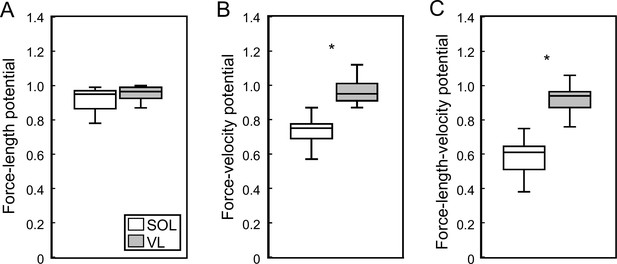
Soleus (SOL, n = 19) and vastus lateralis (VL, n = 14) force-length potential (A), force-velocity potential (B), and overall force-length-velocity potential (C) averaged over the stance phase of running.
*Significant difference between muscles (p<0.05).
-
Figure 2—source data 1
Numerical data represented in the graph 2.
- https://cdn.elifesciences.org/articles/67182/elife-67182-fig2-data1-v1.xlsx
Figure 3
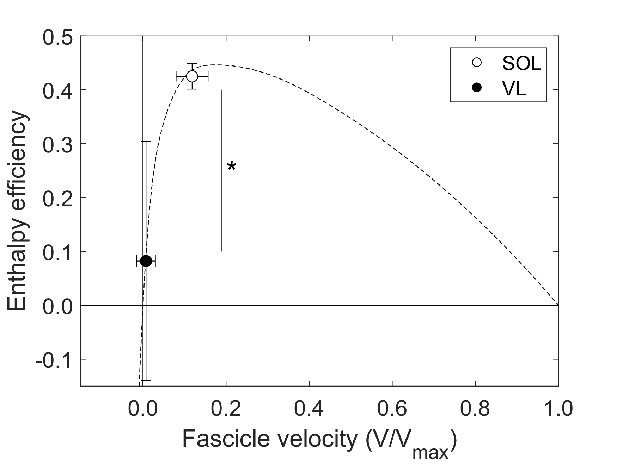
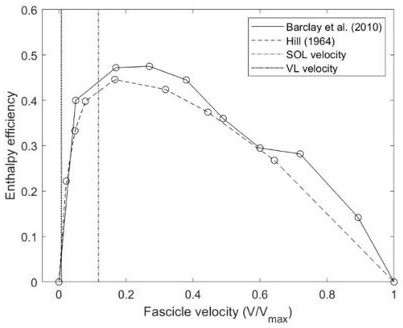
Soleus (SOL, n = 19) and vastus lateralis (VL, n = 14) enthalpy efficiency (mean ± SD) averaged over the stance phase of running onto the enthalpy efficiency-fascicle velocity relationship (dashed line).
*Significant difference between muscles (p<0.05).
-
Figure 3—source data 1
Numerical data represented in the graph 3.
- https://cdn.elifesciences.org/articles/67182/elife-67182-fig3-data1-v1.xlsx
Figure 4
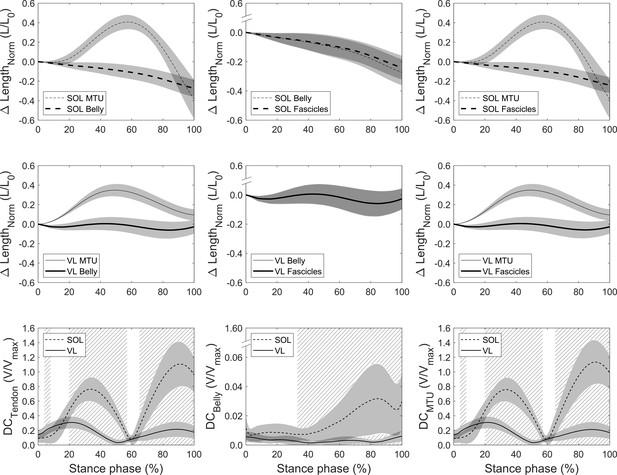
Soleus (SOL, n = 19, top row) and vastus lateralis (VL, n = 14, mid row) muscle-tendon unit (MTU) vs. belly length changes (left), belly vs. fascicle length changes (mid), and MTU vs. fascicle length changes (right) over the stance phase of running with respect to the length at touchdown (0% stance phase).
Differences between curves illustrate the length-decoupling due to tendon compliance, fascicle rotation, and the overall decoupling, respectively. The bottom row shows the resulting velocity-decoupling coefficients (DCs) as the absolute velocity differences between fascicles, belly, and MTU normalized to the maximum shorting velocity (see Materials and methods). Intervals of stance with a significant difference between both muscles are illustrated as hatched areas (p<0.05).
-
Figure 4—source data 1
Numerical data represented in the graph 4.
- https://cdn.elifesciences.org/articles/67182/elife-67182-fig4-data1-v1.xlsx
Figure 5
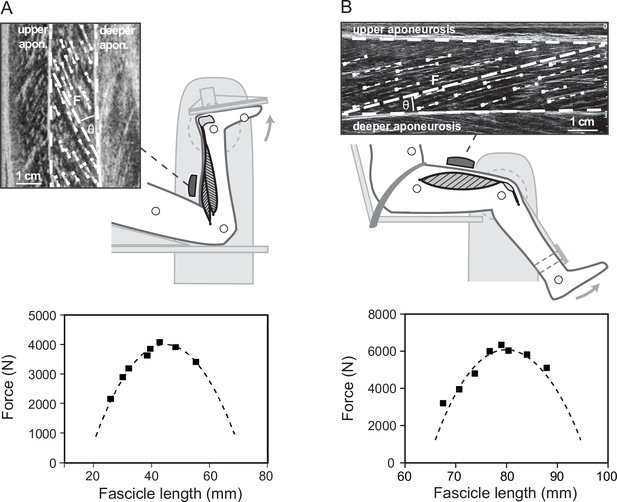
Experimental setup for the determination of the soleus (A) and vastus lateralis (B) force-fascicle length relationship.
Maximum isometric plantar flexions (MVC) at eight different joint angles were performed on a dynamometer. During the MVCs, ultrasound images of the soleus and vastus lateralis were recorded and a representative muscle fascicle length (F) was calculated based on multiple fascicle portions (short dashed lines). Accordingly, an individual force-fascicle length relationship for the soleus and vastus lateralis muscle was derived from the MVCs (squares) by means of a second-order polynomial fit (dashed line, bottom graphs, MVCs and curves of one representative participant).
Author response image 1
Predicted efficiency for running at 5.0 m/s.
Author response image 2
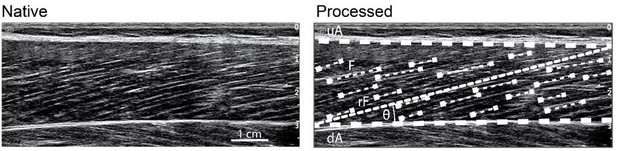
Ultrasound-based determination of muscle fascicle length.
upper (uA) and deeper (dA) aponeurosis, representative reference fascicle (rF) calculated from all identified visible features of multiple fascicles (F).
Author response image 3
Comparison of efficiency-velocity curves provided in literature and assessed operating velocities of soleus (SOL) and vastus lateralis (VL).
Tables
Table 1
Average tendon (DCTendon), belly (DCBelly), and muscle-tendon unit (DCMTU) decoupling coefficients for the soleus (SOL) and vastus lateralis (VL) muscles during the stance phase of running (mean ± SD).
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Muscle-specific economy of force generation and efficiency of work production during human running
eLife 10:e67182.
https://doi.org/10.7554/eLife.67182
