Figures and data in Evolution of diversity in metabolic strategies | eLife

Figures
Additional files

8 figures and 1 additional file

Figures

Figure 1

Download asset Open asset

Snapshots illustrating the beginning, intermediate, and advanced stages of evolution under a linear constraint, $γ = 1$ .

A video of the entire evolutionary process can be found here, frames are recorded every 200 time units until t=30,000 and then, to better illustrate slow neutral evolution, the frame recording times t_i were defined as a geometric progression $t_{i + 1} = 1.006 t_{i}$ . Other parameter values were $s_{j} = 1$ , $μ_{j} K_{j} = 0.1$ for $j = 1, 2, 3$ , and $δ = 1$ .

Figure 2

Download asset Open asset

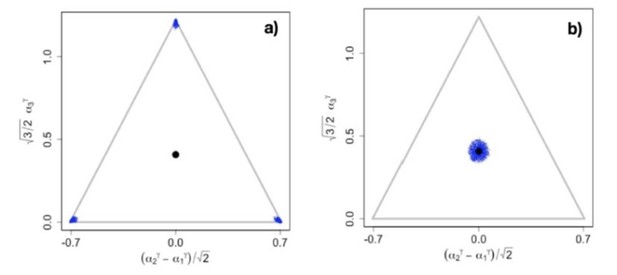
Example of evolutionary dynamics for $γ = 1.1$ , showing convergence to the singular point given by Equation 4 (and indicated by the black dot), but no subsequent diversification.

The corresponding video can be found here , each frame in the video is separated by 1,000 time steps. Other parameter values were $s_{j} = 1$ , $μ_{j} K_{j} = 0.1$ for $j = 1, 2, 3$ , and $δ = 0.25$ .

Figure 3

Download asset Open asset

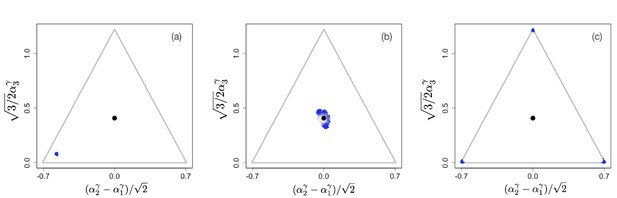
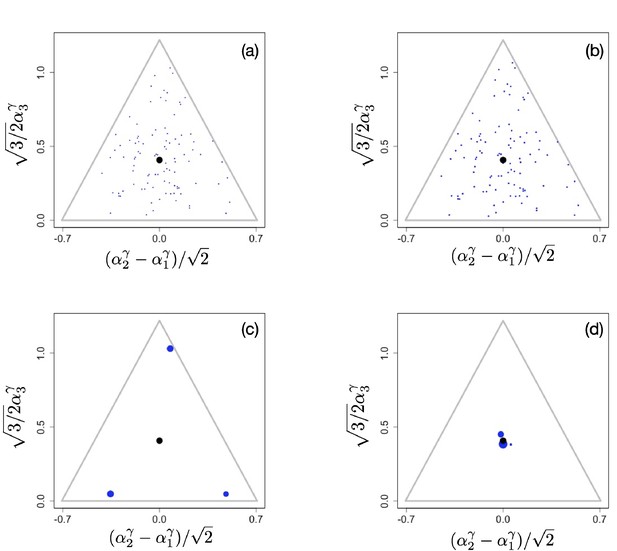
Example of evolutionary dynamics for $γ = 0.9$ , showing initial convergence to the singular point (indicated by the black dot) and subsequent diversification into three specialists, each consuming exclusively one of the three resources.

The corresponding video can be found here, each frame in the video is separated by 1,000 time steps. Other parameter values were $s_{j} = 1$ , $μ_{j} K_{j} = 0.1$ for $j = 1, 2, 3$ , and $δ = 0.25$ .

Appendix 1—figure 1

Download asset Open asset

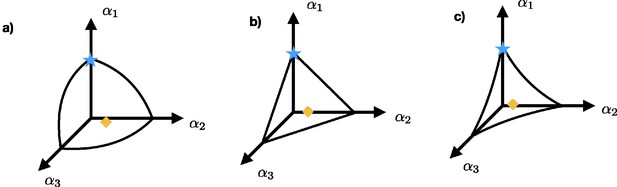
Three possible surfaces defined by a tradeoff: (a) shows the concave surface for the case $γ > 1$ , while (b) and (c) show the surface for the cases $γ = 1$ and $γ < 1$ , respectively.

The blue star and the orange diamond represent possible strategies. Individuals with strategy represented by the blue star obtain their nutrients only from resource s₁ while the individuals that adopt strategy indicated by the orange diamond uptake nutrients from all three resources.

Appendix 1—figure 2

Download asset Open asset

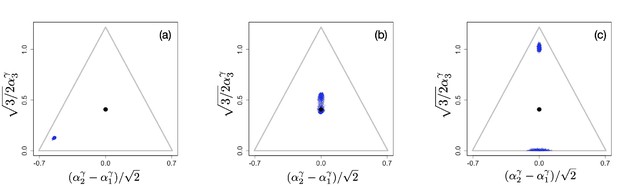
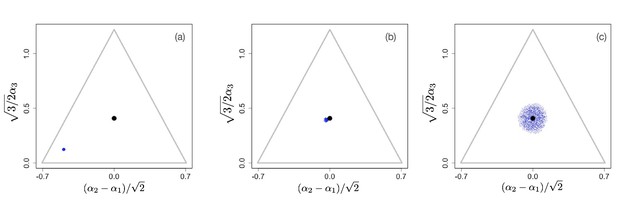
Example of evolutionary dynamics for $γ_{1} = γ_{2} = 1.1$ and $γ_{3} = 0.9$ , showing convergence to the singular point and subsequent diversification only in the $α_{3}$ direction.

(Note that the dynamics are shown in the original α-phenotype space.) The corresponding video can be found here, each frame in the video is separated by 2,000 time steps. Other parameter values were $s_{j} = 1$ , $μ_{j} K_{j} = 0.1$ for $j = 1, 2, 3$ , and $δ = 0.25$ .

Appendix 1—figure 3

Download asset Open asset

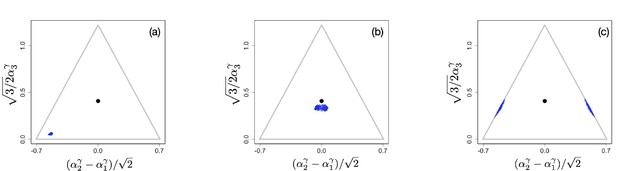
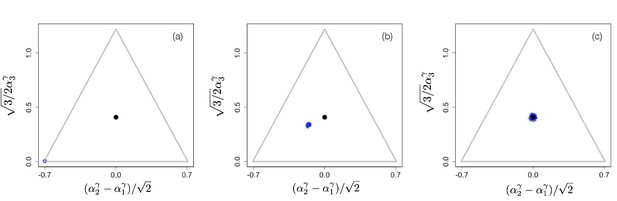
Example of evolutionary dynamics for $γ_{1} = γ_{2} = 0.9$ and $γ_{3} = 1.2$ , showing convergence to the singular point and subsequent diversification only in $α_{1} - α_{2}$ directions.

(Note that the dynamics are shown in the original α-phenotype space.) The corresponding video can be found here, each frame in the video is separated by 2000 time steps. Other parameter values were $s_{j} = 1$ , $μ_{j} K_{j} = 0.1$ for $j = 1, 2, 3$ , and $δ = 0.25$ .

Appendix 1—figure 4

Download asset Open asset

Initial population configuration of 100 randomly placed clusters in the phenotypic simplex (a), final configurations after 5,000,000 time units for $γ = 1$ (b), $γ = 0.9$ (c), and $γ = 1.1$ (d). Videos of the entire ecological processes can be found here, time interval between frames increased as a geometric progression, $t (i + 1) = 1.05 t (i)$ . Other parameter values were $s_{j} = 1$ , $μ_{j} K_{j} = 0.1$ for $j = 1, 2, 3$ , and $δ = 0.25$ .

Author response image 1

Download asset Open asset

Snapshots illustrating the end of the evolutionary dynamics for (a) = 0.

99 and (b) = 1.01. The video of the entire evolutionary process can be found at https://figshare.com/s/f65ed0bf9b4305e9018f .

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/67764/elife-67764-transrepform-v2.pdf
Download elife-67764-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Rodrigo Caetano
Yaroslav Ispolatov
Michael Doebeli

(2021)

Evolution of diversity in metabolic strategies

eLife 10:e67764.

https://doi.org/10.7554/eLife.67764

Sign up for email alerts

Privacy notice