Flexible use of memory by food-caching birds
Figures
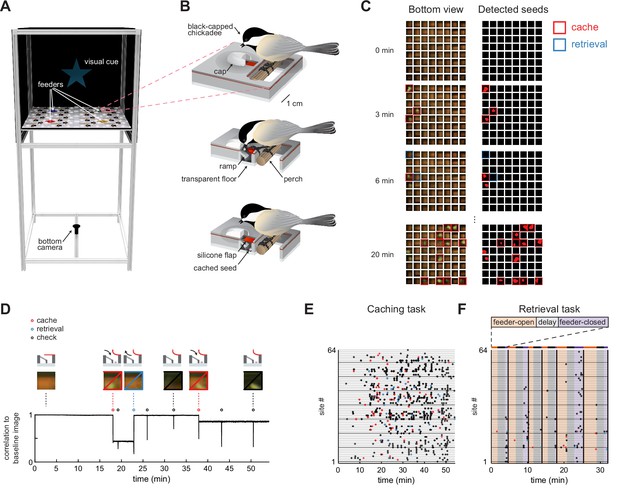
Behavioral paradigm for food caching and retrieval in chickadees.
(A) Rendering of the behavioral setup. For clarity, the front wall that contains doors of the arena is removed. Pink box highlights one cache site.(B) Illustration of a chickadee at a cache site. Top: chickadee prior to caching. Middle: cross-section of the cache site, with a chickadee pulling open the silicone flap to deposit a seed. Bottom: cross-section of the cache site after the seed was cached. (C) Left: video frames from the bottom camera showing all 64 cache sites at four timepoints within a behavioral session. Right: real-time detection of cached seeds. Red area indicates shape enclosed by the detected seed contour. (D) Detection of events at one example cache site in one behavioral session. Top: cartoon of the bird’s interactions with the site at several time points. Middle: video frames from the bottom camera at the corresponding time points. Bottom: Pearson correlation of each video frame with the image of the same cache site when empty. Caches create sustained decreases in the correlation, whereas site checks create transient decreases. (E) Ethogram of all behavioral events in an example session of the Caching task. Colored circles correspond to caches, retrievals, and site checks, as in (D). (F) Same as (E), for the Retrieval task. Colored regions indicate the phase of the trial. Black vertical lines denote trial boundaries.
Caching task.
One min of a session of the Caching task. The bird can be seen drawing food from multiple feeders as well as caching, retrieving, and checking sites. Site interactions are indicated by text on the back wall of the apparatus.
Retrieval task.
One trial of the Retrieval task. The bird can be seen caching into one site in the feeder-open phase, then checking and retrieving the food in the feeder-closed phase. Task phase is indicated by text on the back wall of the apparatus. The delay phase of the task is truncated for clarity.
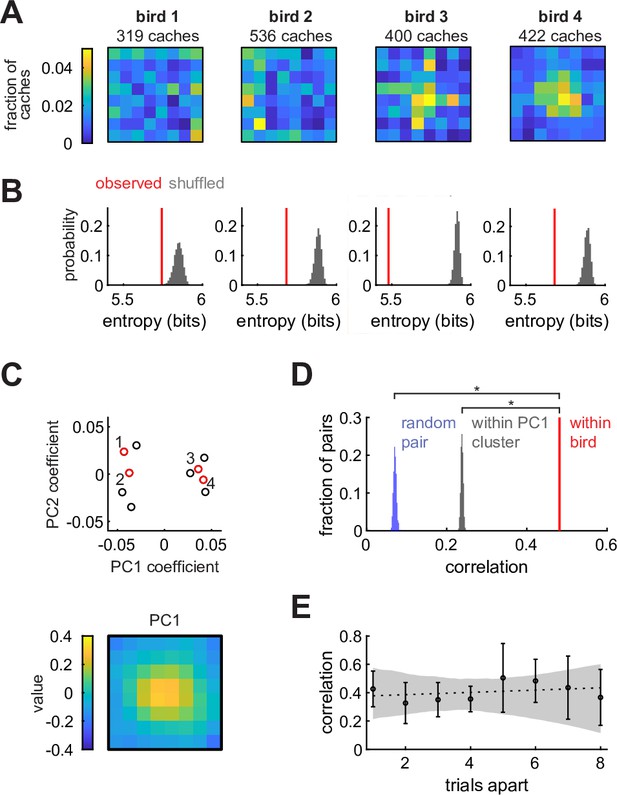
Chickadees exhibit idiosyncratic and stable biases in the locations of caches.
(A) Probability distributions of cache locations across all sessions for four example birds. Distributions are denoted by in the text. (B) Red lines: entropy values of the spatial distributions shown in (A). Gray histograms: entropy values for simulated caches drawn from a uniform distribution. Number of simulated caches was the same as in the observed data. (C) Principal component analysis of values. Top: coefficients of the first two principal components for all birds. Red circles and numbers indicate birds shown in (A) and (B). Bottom: the first principal component. Birds cluster into center-preferring and edge-preferring groups. (D) Pearson correlation of between subsets of all sessions paired within bird, between different birds, and between birds selected from the same PC1 cluster shown in (C). (E) Pearson correlation of between pairs of trials at different trial lags. Values are medians across birds. Error bars: sem. Dashed line: linear regression. Gray shade: 95% confidence interval of linear regression fit to bootstrapped birds.
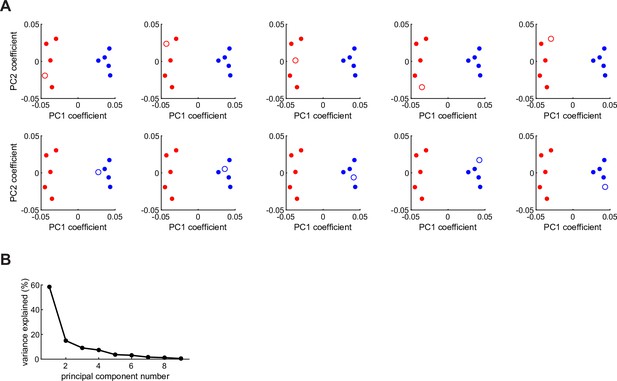
Validation of the clusters of values (A) Assignment of birds to two clusters using k-means clustering of values and its cross validation.
For each plot, the k-means clustering of values was performed on 9 of 10 birds. The remaining bird was then assigned to the cluster with the nearest centroid. Symbols represent individual birds’ values along the top two principal components, calculated using all 10 birds. Open circle: left-out bird. Color denotes cluster assignment. In all 10 cases, analysis assigned the left-out bird to the same cluster as when that bird was not left-out. (B) Explained variance for each principal component.

Chickadees exhibit idiosyncratic and stable biases in the locations of checks.
(A) Distributions of check locations across all sessions for four example birds. Distributions are denoted by in the text. (B) Red lines: entropy values of the spatial distributions shown in (A). Gray histograms: entropy values for simulated checks drawn from a uniform distribution. Number of simulated checks was the same as in the observed data. (C) Principal component analysis of values. Top: coefficients of the first two principal components for all birds. Red circles and numbers indicate birds shown in (A) and (B). Bottom: the first principal component. (D) Pearson correlation of between subsets of all sessions paired within bird, between different birds, and between birds selected from the same PC1 cluster shown in (C). Although birds do not visibly cluster in (C), we defined ‘clusters’ as groups of birds whose first principal component was <0 and >0 for analogy with Figure 2. (E) Pearson correlation of between pairs of sessions at different time lags. Values are medians across birds. Error bars: sem. Dashed line: linear regression. Gray shade: 95% confidence of linear regression fit to boot-strapped birds. Slope of the regression was not significantly different from zero (p = 0.22). (F) Pearson correlation of between all sessions of the Caching and all sessions of the Retrieval tasks. Red line: median within bird correlation. Grey histogram: correlation of randomly paired birds. Individual birds exhibit values that are more similar between Caching and Retrieval tasks than expected from random pairing (p < 0.005).
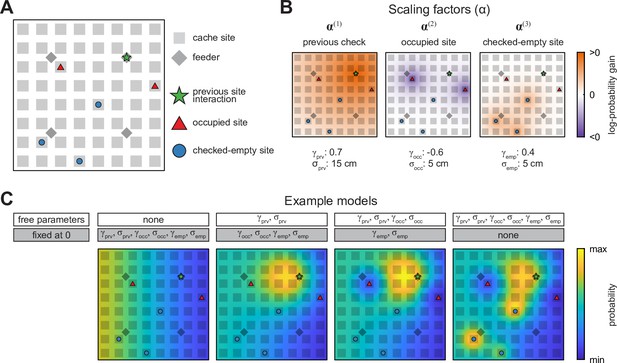
Schematic of the probabilistic behavioral models.
Models here compute the probability of caching into a particular site in the Caching task. Equivalent models are used for the probability of checking a particular site in the Retrieval task. (A) Schematic of the arena at an example time point in the Caching task depicting ‘special locations’ in the arena: previous site interaction, occupied sites, and checked-empty sites. (B) Examples of scaling factors that change with proximity to each of the special locations shown in (A). Probability distribution of caching into different sites is computed by multiplying all scaling factors by . (C) Example models. For each model, some parameters are fixed at 0, while others are free and fit using maximum-likelihood estimation. For free parameters, examples shown here use the same values as in (B). All four models are plotted on the same color scale.
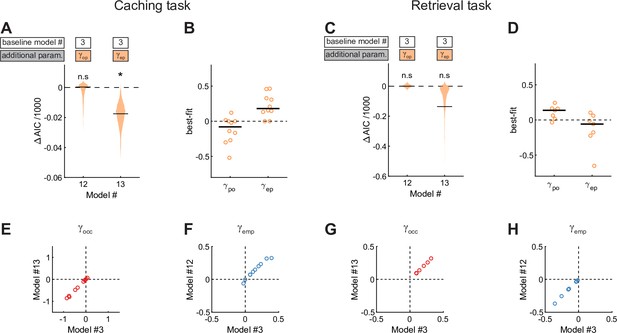
Non-linear interaction of terms.
(A) Performance of Model #12 and Model #13 applied to the Caching task, plotted as in Figure 4A. Model #12 introduces an extra free parameter to model the interaction between the previous site and occupied sites. If we express the scaling factor for the previous site (Equation 5) as and the scaling factor for occupied sites (Equation 6) as , then the interaction term is defined as . Equations that use the scaling factors (Equations 10; 11) now operate on six, rather than only five factors. Model #13 analogously introduces a free parameter to model the interaction between the previous site and checked-empty sites (derived from expressions in Equations 5; 7). Model #12 did not improve the fit (p = 0.46), but Model #13 did (p < 0.01). Therefore, there was a nonlinear interaction between the effect of the previous site and the effect of checked-empty sites (B) Best-fit values of and applied to individual birds in the Caching task, plotted as in Figure 4B. Best-fit values are –0.08 ± 0.08 and 0.18 ± 0.07, respectively. A positive value of indicates a supralinear interaction: birds had a particularly strong preference for caching into sites that were close to the previous site and were checked-empty. (C) Same as (A), but for models applied to the Retrieval task. Neither model significantly improved the fit (p = 0.85 and p = 0.054, respectively). (D) Same as (B), but for models applied to the Retrieval task. Best-fit values are 0.13 ± 0.05 and –0.06 ± 0.11, respectively. (E) Values of across birds in the Caching task compared between Model #3 and Model #13. Values are largely unchanged between the two models. Therefore, using a simpler model that did not account for nonlinear interactions (Model #3) did not distort the results related to the mnemonic parameter (F) Same as for (E) but for parameter compared between Model #3 and Model #12. (G–H) Same as (E–F), but applied to the Retrieval task.
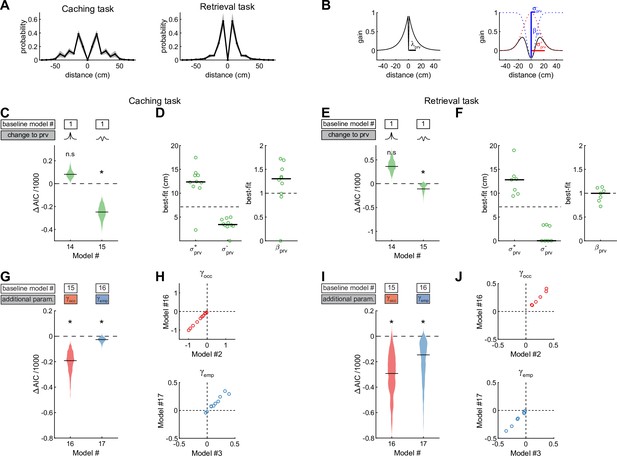
Using alternate shapes for the previous site scaling factor.
(A) Left: distribution of caches across different distances from the previous site. Right: distribution of site checks across different distances from the previous site. Black trace: mean probability across birds. Gray: 95% confidence interval calculated by bootstrapping birds. In both tasks, probability decreases with distance, but is also low at small distances. In the main text, the previous site scaling factor is modeled using a Gaussian with a notch as 0 (Equation 5), which captures the basic features of these traces. (B) Schematic of two alternate functions that were tested instead of a notched Gaussian. Left: Notched exponential function, parametrized by decay . Right: Mexican hat function parameterized by two widths for the positive and negative Gaussian components ( and , respectively) and the amplitude of the negative Gaussian (). The amplitude of the exponential on the left and the amplitude of the positive Gaussian on the right are both 1; however, the entire function is scaled by in the models (see below). (C) Performance of Models #14 and # 15 applied to the Caching task, plotted as in Figure 4A. These models are identical to Model #1, but instead of the notched Gaussian function use a notched exponential scaled by or the Mexican hat function scaled by , respectively. Model #14 did not improve the fit (p = 0.99), whereas Model #15 did (p < 0.001). Therefore, a Mexican hat function better describes the proximity effect than a notched Gaussian. (D) Best-fit values of parameters of , and applied to individual birds in the Caching task, plotted as in Figure 4B. Dashed line on the left: distance between cache sites. (E–F) Same as (C–D), but applied to the Retrieval task. p = 1, p < 0.005 respectively. (G) Performance of Models #16 and # 17 in the Caching task, plotted as in Figure 4A. These models used a Mexican hat function to model the proximity effect and introduced the mnemonic parameters and to quantify the spatial extent of the effect of occupied and checked-empty sites on behavior, respectively. In other words, these models were like Models #2 and #3 (see main text), but used a Mexican hat function instead of a Gaussian for the previous site scaling factor. Both models improved the fit (p < 0.005). (H) Values of the mnemonic parameters and across birds, compared between Model #2 and Model #16, and Model #3 and Model #17 respectively, applied to the Caching task. In both cases, the value of the parameters is unchanged between models. Therefore, using a simpler Gaussian scaling factor for the proximity effect (as in Models #2 and #3) did not distort the values of the mnemonic parameters compared to those produced by the more complex Mexican hat scaling factor (Models #16 and #17). (I–J) Same as (G–H), but applied to the Retrieval task.
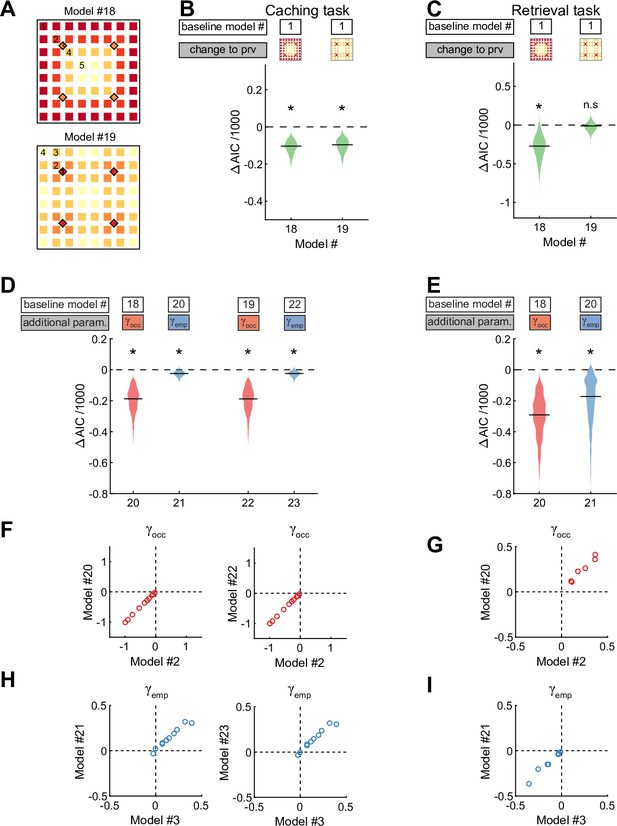
Using different sigma values across the arena.
(A) Schematic of how the arena is subdivided to assign multiple different values of at different locations. Left: grouping of locations by distance to arena walls. Right: grouping of locations by distance to feeders. (B) Performance of Models #18 and #19 applied to the Caching task, plotted as in Figure 4A. These models are identical to Model #1, but use a different parameter for the width of the Gaussian scaling factor instead of a single value for the entire arena. In both cases, using multiple sigma values improves the model fit (p < 0.001). (C) Same as (B), but applied to the Retrieval task. In this case, grouping locations by distance to the wall, but not distance to feeders, improves the model fit (p < 0.02 and p = 0.18, respectively). (D) Performance of Models #20-#23 applied to the Caching task, plotted as in Figure 4A. These models used different values of sigma across the arena (as Models shown in (B–C)) and introduced free parameters and to quantify the spatial extent of the effect of occupied and checked-empty sites on behavior, respectively. In all cases, models were improved by the introduction of these mnemonic parameters (p < 0.005). (E) Same as (D), but for models applied to the Retrieval task. Note that since Model #19 was not an improvement over Model #1, Models #22 and #23 were omitted. Again, mnemonic parameters improved the model fit in all cases (p < 0.05). (F) Values of the mnemonic parameter across birds, compared between Model #2 and Models #20 and #22, applied to the Caching task. Note that in all cases, the value of is unchanged between models. Therefore, using a single sigma value across the entire arena for the proximity effect (as in Model #2) did not distort the values of the mnemonic parameter compared to those produced by the more complex models using different sigma values (Models #20 and #22). (G) Same as (F), but applied to the Retrieval task. (H) Same as (F), but analyzing the mnemonic parameter . (I) Same as (H), but applied to the Retrieval task.
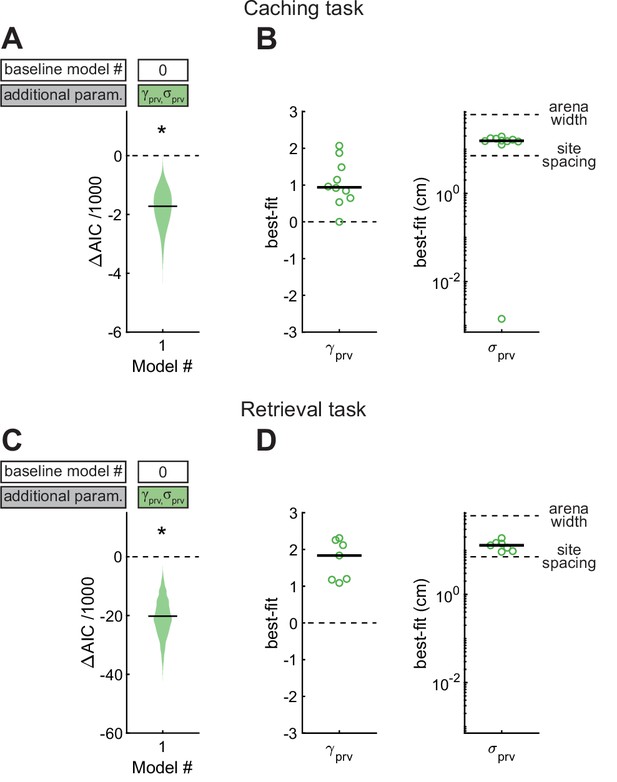
Effect of proximity to the previous site in Caching and Retrieval tasks.
(A) Comparison of Model #1 to Model #0 applied to the Caching task. Here and in subsequent figures, ΔAIC indicates the difference in AIC between the model being considered (in this case Model #1, labeled on the x-axis) and the baseline model (in this case Model #0, labeled in the white box). Compared to Model #0, Model #1 uses two additional free parameters ( and ), specified in the colored box. Horizontal black line: ΔAIC value for caches pooled from all birds. Shaded area: distribution of 1000 ΔAIC values on data bootstrapped across birds. Values less than 0 indicate model improvement. Asterisk indicates statistically significant improvement. (B) Best-fit values of model parameters prv and σprv for Model #1 applied to the Caching task. Symbols indicate values for individual birds. Black line: median values across birds. (C, D) Same as (A, B), but for models applied to the Retrieval task.
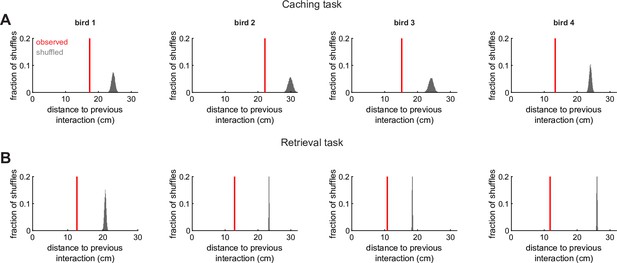
Corroboration of the proximity effect.
(A) Distance between the location of the site check preceding a cache (”previous site”) and the site of the cache. Red: mean of observed distances. Gray: distribution of the mean for shuffled distances, in which caches and checks were paired randomly. All four example birds cached closer to the previous site than expected by chance (p < 0.001). (B) Same as (A) but for the Retrieval task.
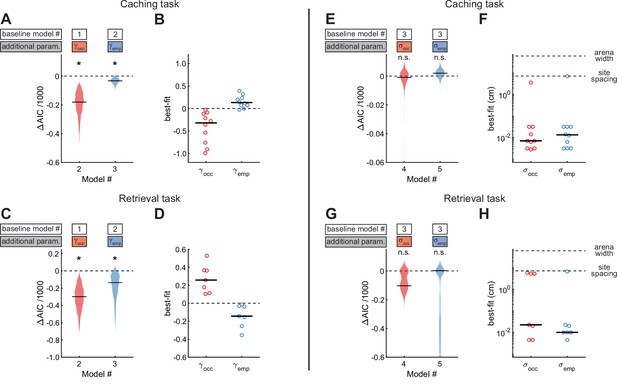
Site-specific, opposing effects of site content on behavior in Caching and Retrieving tasks.
(A) Performance of Models #2 and #3 applied to the Caching task, plotted as in Figure 4A. These models introduce free parameters to quantify the effect of occupied and checked-empty sites on behavior. (B) Best-fit values of and applied to the Caching task, plotted as in Figure 4B. (C, D) Same as (A, B) but for models applied to the Retrieval task. (E) Performance of Models #4 and #5 applied to the Caching task, plotted as in Figure 4A. These models introduce free parameters to quantify the spatial extent of the effect of occupied and checked-empty sites on behavior. (F) Best-fit values of and applied to individual birds in the Caching task, plotted as in Figure 4B. (G, H) Same as (E, F), but for models applied to the Retrieval task.
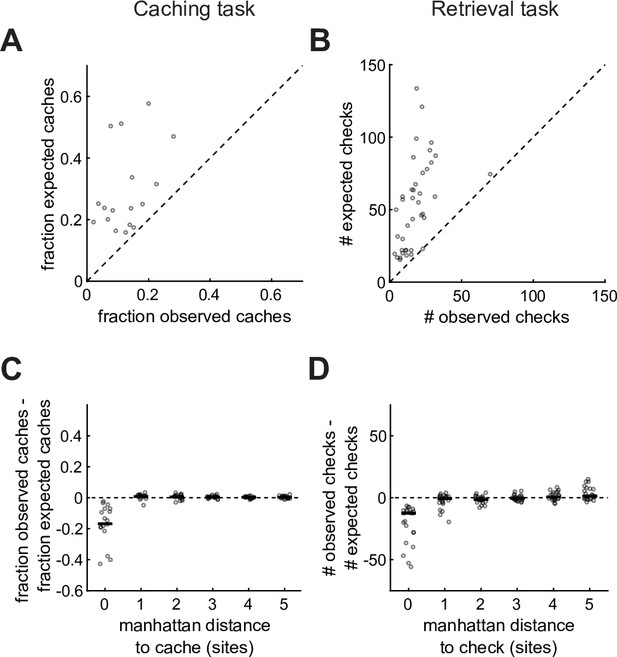
Corroboration of the effects of specific site contents on behavior.
(A) Observed and expected fractions of caches made into occupied sites. Each symbol indicates fractions for one bird. Expected fraction is calculated by randomly drawing, at the time of each cache, a simulated cache location from the distribution . Random drawing was performed 1000 times, and fractions of occupied sites were averaged across the draws. Chickadees cached into occupied sites less often than expected by chance. (B) The number of observed and expected checks required by the bird to find a cache in the Retrieval task. For each cache, we ordered all trials of the same bird across all sessions and concatenated the sequences of checks made in those trials. For calculating the observed number of checks, the actual trial containing the cache was first in the order, and the remaining trials were ordered randomly. For calculating the expected number of checks, all trials were ordered randomly. In both cases, we asked where in the concatenated sequence the earliest check of the cache site occurred. The median across 1,000 random orders was taken. For most caches, this analysis compared how many attempts the bird required to find a cache vs. how many attempts a trajectory taken from a different trial would require to find that same cache. However, in a small number cases when the bird failed to find the cache, this analysis equally penalized both the observed and the expected numbers. Each symbol is the median value across all caches made into a particular site (1-64), including only those caches sites where at least two birds cached at least three times each (40 sites total). At all sites, caches were found in fewer attempts than expected by chance (C) Difference between the observed and expected fractions of caches into occupied sites, calculated as in (A). For distance = 0, this analysis uses occupied sites, as in (A). For distances > 0, this analysis instead takes the average across all sites in the arena at the corresponding manhattan distance away from an occupied site. Black line indicates the median across all birds. Birds avoided caching into occupied sites, but did not avoid caching into sites even at a distance of 1 site away (i.e. the effect was site-specific). (D) Analysis described in (B), performed for different Manhattan distances away from the cache site. For each site j in the arena, we considered the set of all sites Sdj that are located at a Manhattan distance d from j. We then computed the median difference between observed and expected values for each of the sites in Sdj across all caches made into j. Finally, we took this median value from the site in Sdj that has the smallest absolute value. These values are plotted for the same 40 sites as in (B). Black line is the median across all sites. Birds showed attraction to occupied sites in the Retrieval task, but did not show attraction even at a distance of 1 site away (i.e. the effect was also site-specific).
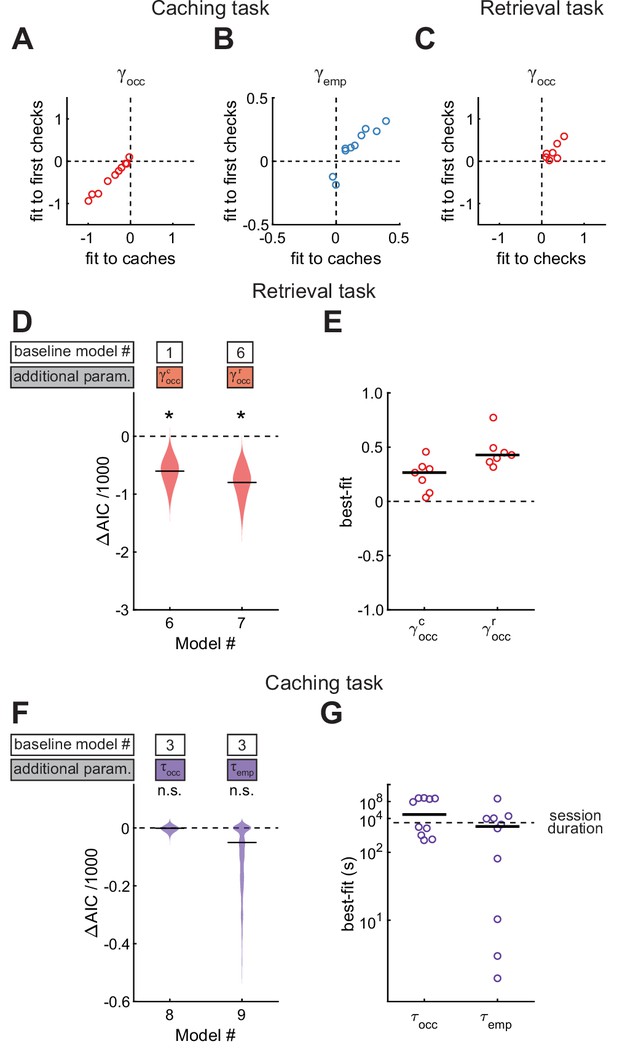
Results are best explained by long-lasting memories.
(A, B) Values of parameters across birds, compared between models applied to caches or first checks in the Caching task. Values of are from Model #2, and values of are from Model #3. (C) Values of across birds, compared between Model #2 applied to checks or the same model applied to first checks in the Retrieval task. (D) Performance of Models #6 and #7 applied to the Retrieval task, plotted as in Figure 4A. These models introduce free parameters to separately quantify the effects of caches and recaches on the site checking behavior. (E) Best-fit values of and applied to individual birds in the Retrieval task, plotted as in Figure 4B. (F) Performance of Models #8 and #9 applied to the Caching task, plotted as in Figure 4A. These models introduce free parameters and to quantify the decay of and over time since the site was last checked by the bird. (G) Best-fit values of and applied to individual birds in the Caching task, plotted as in Figure 4B.
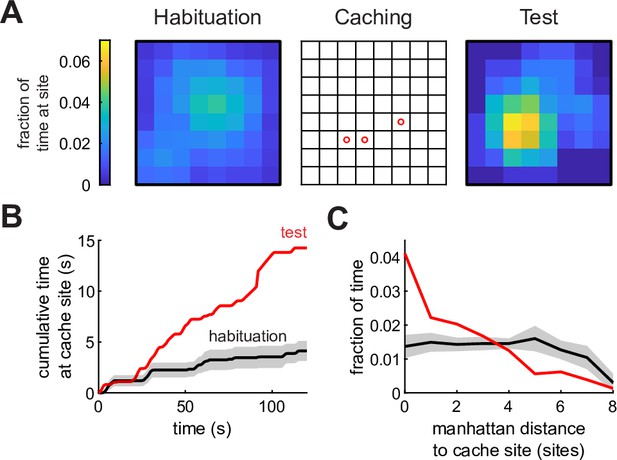
Chickadees return to cache locations even if seeds have been removed.
(A) Example behavioral session in the experiment controlling for olfactory cues. Left: occupancy of the chickadee in the first 5 min of the habituation session. Center: locations of caches made in the caching session. Right: spatial occupancy in the first 60 s of the test session. For the left and right panel, any uninterrupted time spent >10 s at one site (such as during eating or grooming) was excluded. (B) Cumulative time spent at the cache site before caching (habituation session) and after caching (test session). Red trace: mean across all test sessions (n = 6) in all birds. Black trace: mean across all habituation sessions. Gray:± sem across sessions. Time 0 is the beginning of the session. (C) Fraction of time spent at each cache site in first 120 s of the session, as a function of Manhattan distance away from the nearest cache site. Red trace: mean across all sessions in all birds. Gray:± sem across sessions. Effect is observed not only at the cache site, but also at nearby sites because the bird often spent time at a neighboring site visually inspecting the site where a cache was expected.
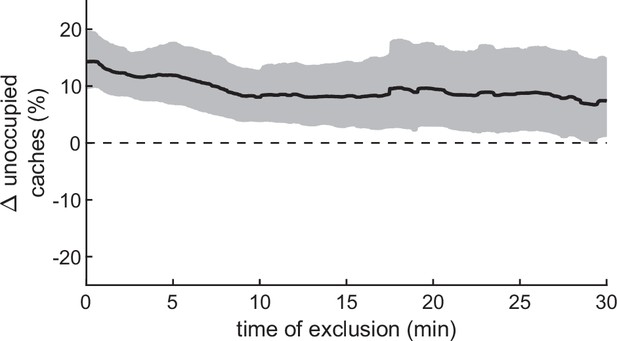
Birds preferentially cache into unoccupied sites even when sites have not been recently checked.
For each bird, we found all caches into sites that have not been checked in the t minutes prior to the cache. For these caches, we calculated the difference between the observed and expected fractions of caches into occupied sites, calculated as in Figure 5—figure supplement 1A. To calculate the expected fraction of caches in occupied sites, any arena site that had been checked in the preceding t minutes was excluded from the calculation of the distribution. Black trace: Average across birds. Gray: 95% confidence calculated by bootstrapping across birds. Birds continue preferentially caching into empty sites even after not checking sites for 30 min.
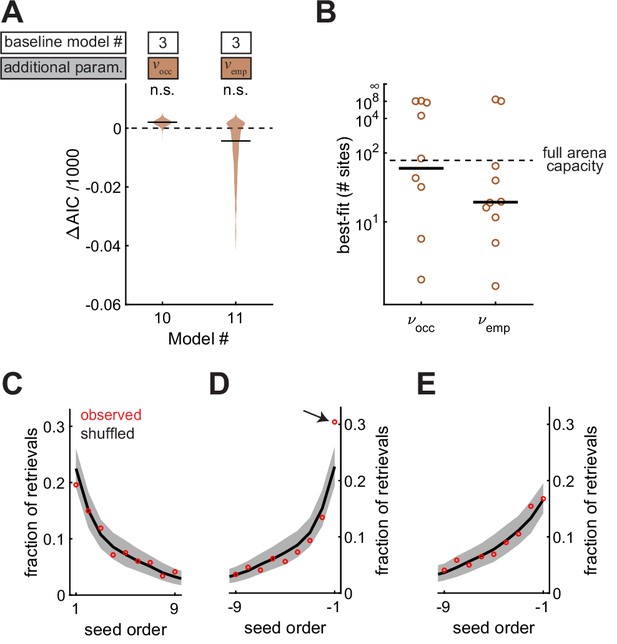
Memories are high capacity, and accessed in arbitrary order.
(A) Performance of Models #10 and #11 applied to the Caching task, plotted as in Figure 4A. These models introduce free parameters and to quantify the decay of and as either the number of occupied sites or the number of checked-empty sites in the arena increases, respectively. (B) Best-fit values of and applied to individual birds in the Caching task, plotted as in Figure 4B. (C) Fraction of retrievals as a function of order in which seeds were caches. Order is aligned to the first cache. Red marker: mean observed fraction across birds. Black line: average value expected from retrieving seeds in a random order. Grey: 95% confidence interval of retrievals made in a random order. (D) Same as (C), but aligned to the most recent cache. Arrow indicates the only point that was significantly outside the 95% confidence interval of shuffled data. (E) Same as (D), but with transient caches eliminated. Transient caches are those that are retrieved without leaving the perch.
Tables
Summary of model performance.
Statistical analysis for all 12 models (0 through 11) presented in the Results section. Each model is compared to one of the previous models using bootstrap analysis of AIC values (see Materials and methods). p-values < 0.05 are emphasized in bold. Model #0 does not have corresponding p-values because it was the baseline model that was not compared to anything. Some models were only fit to data from the Caching or Retrieval task; in these cases, a hypen indicates that the corresponding fit was not performed.
| Model # | Free parameters | Compared toModel # | Model improvement? | |
|---|---|---|---|---|
| Caching task p-value | Retrieval task p-value | |||
| 0 | none | - | - | - |
| 1 | 0 | < 0.001 | < 0.001 | |
| 2 | 1 | < 0.001 | < 0.001 | |
| 3 | 2 | < 0.001 | 0.015 | |
| 4 | 3 | 0.48 | 0.35 | |
| 5 | 3 | 0.93 | 0.42 | |
| 6 | 1 | - | < 0.001 | |
| 7 | 6 | - | < 0.001 | |
| 8 | 3 | 0.48 | - | |
| 9 | 3 | 0.24 | - | |
| 10 | 3 | 0.97 | - | |
| 11 | 3 | 0.29 | - | |
Contributions of different factors to behavior.
Statistical analysis of all parameters mentioned in the Results section, which indicate the contribution of different factors to behavior. Best fit parameter values are indicated as median ± standard error of the median across all birds (N = 10 in the Caching task and N = 7 in the Retrieval task). Significance across birds is calculated using a one-sided Wilcoxon rank sum test to determine whether values across the population are significantly different from 0. The fraction of birds that are individually significant is calculated by bootstrapping the behavioral sessions of each bird. A p-value of 0.05 is used to assign significance in this case. See Materials and methods for details.
| Parameter | Best-fit parameter value | Significance across birds | Fraction of individually significant birds | |||
|---|---|---|---|---|---|---|
| Caching task | Retrieval task | Caching task p-value | Retrieval task p-value | Caching task | Retrieval task | |
| 0.94 ± 0.21 | 1.83 ± 0.42 | < 0.001 | < 0.001 | 8/10 | 7/7 | |
| –0.32 ± 0.17 | 0.26 ± 0.09 | < 0.001 | 0.008 | 8/10 | 7/7 | |
| 0.13 ± 0.05 | –0.14 ± 0.07 | 0.005 | 0.008 | 6/10 | 5/7 | |
| ,first check | –0.28 ± 0.17 | 0.18 ± 0.10 | 0.005 | 0.008 | 8/10 | 2/7 |
| ,first check | 0.12 ± 0.05 | - | 0.042 | - | 6/10 | - |
| - | 0.42 ± 0.05 | - | 0.008 | - | 7/7 | |
| - | 0.26 ± 0.07 | - | 0.008 | - | 6/7 | |
Masks for different subsets of interactions.
| Subset of interactions | ||
|---|---|---|
| All caches in the Caching task | | |
| First checks in the Caching task. This mask includes the first check that the bird made after retrieving each seed that was subsequently cached (i.e. it does not include checks made after retrieving seeds that were subsequently eaten without caching). | | |
| All checks in the feeder-closed phase of the Retrieval task | | |
| All checks up to and including finding a cache (i.e. making the first check of an occupied site) in the feeder-closed phase of the Retrieval task. If no cache is found in the feeder-closed phase of the trial, this includes all checks up until the end of the trial. | | |
| First checks in the feeder-closed phase of the Retrieval task. This mask includes the first check made during the feeder-closed phase of each trial. | | |
Permitted ranges of parameters, , for main models.
| Model index | Parameter | # free param | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter index () | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 0 | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | 0 |
| 1 | (-∞,∞) | [0,∞) | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | 2 |
| 2 | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | {0} | 3 |
| 3 | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | (-∞,∞) | {0} | {0} | {0} | {0} | {0} | {0} | {0} | 4 |
| 4 | (-∞,∞) | [0,∞) | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | {0} | {0} | {0} | {0} | {0} | {0} | 5 |
| 5 | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | (-∞,∞) | [0,∞) | {0} | {0} | {0} | {0} | {0} | {0} | 5 |
| 6 | (-∞,∞) | [0,∞) | {0} | {0} | {0} | {0} | (-∞,∞) | {0} | {0} | {0} | {0} | {0} | 3 |
| 7 | (-∞,∞) | [0,∞) | {0} | {0} | {0} | {0} | (-∞,∞) | (-∞,∞) | {0} | {0} | {0} | {0} | 4 |
| 8 | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | (-∞,∞) | {0} | {0} | {0} | [0,∞) | {0} | {0} | {0} | 5 |
| 9 | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | (-∞,∞) | {0} | {0} | {0} | {0} | [0,∞) | {0} | {0} | 5 |
| 10 | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | (-∞,∞) | {0} | {0} | {0} | {0} | {0} | [0,∞) | {0} | 5 |
| 11 | (-∞,∞) | [0,∞) | (-∞,∞) | {0} | (-∞,∞) | {0} | {0} | {0} | {0} | {0} | {0} | [0,∞) | 5 |





