Noisy metabolism can promote microbial cross-feeding
- Lewis-Sigler Institute for Integrative Genomics, Princeton University, United States
- Department of Molecular Biology, Princeton University, United States
Figures
Figure 1
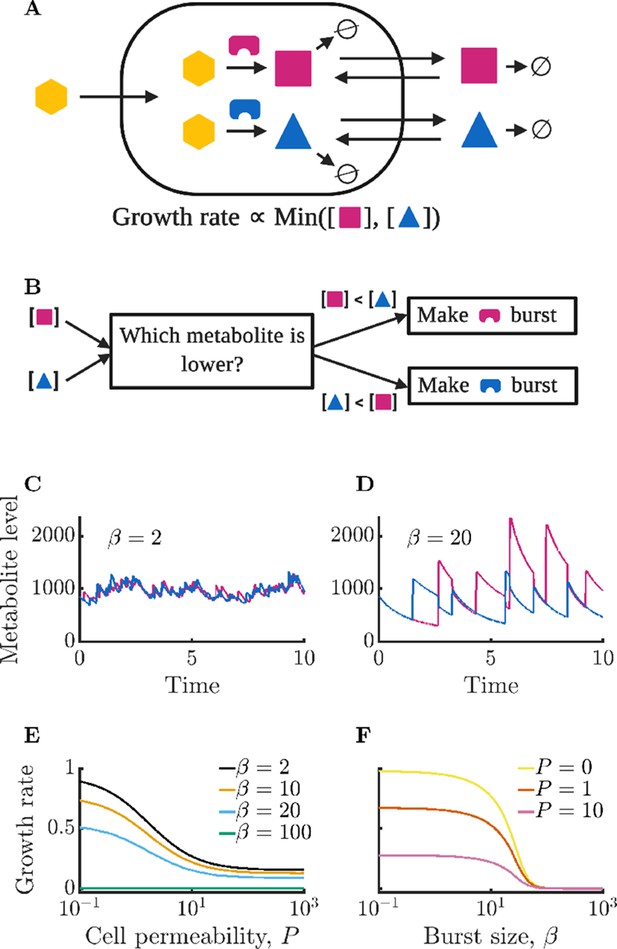
Isolated bacterial cells suffer negative growth effects from noisy enzyme regulation and metabolite leakage.
(A) Schematic of modeled intracellular dynamics. Cells import an external nutrient (yellow hexagon) that can be converted by enzymes (magenta and blue) into two essential metabolites. Metabolites passively exchange with the extracellular medium (‘leakage’), and degrade at a fixed rate. The two metabolites are used for growth in accord with Liebig’s law of the minimum. (B) Schematic of dynamic enzyme regulation scheme: the type of enzyme produced is always the one associated with the lower metabolite pool. (C) Metabolite timecourse of a cell that produces enzymes in small bursts. See Equations 1; 2 for details; parameters , , , , , , . Time is normalized by the inverse of the maximum steady-state growth rate (). (D) Metabolite timecourse of a cell that produces enzymes in large bursts. Same parameters as in C but with . (E) Average growth rate of an isolated cell for differing values of permeability; parameters as in C and D except as specified. Growth rate is normalized to the maximum possible growth rate, i.e. with perfect regulation and zero permeability. (F) Average growth rate of an isolated cell for differing values of burst size. Parameters as in C and D except as specified.
Figure 2
Bacterial cells can compensate for noisy enzyme regulation and increase growth rate by exchanging metabolites within a clonal community.
(A) Schematic of multi-cell metabolism model. Individual cells regulate their own enzyme levels, but metabolites leak into the local medium and can be used by other cells in the community. (B) Intracellular metabolite coefficient of variation (CV) for a community of 10 cells as a function of cell permeability. (C) Average growth rate for community of 10 cells as a function of cell permeability. Parameters in B and C same as in Figure 1E.
Figure 3
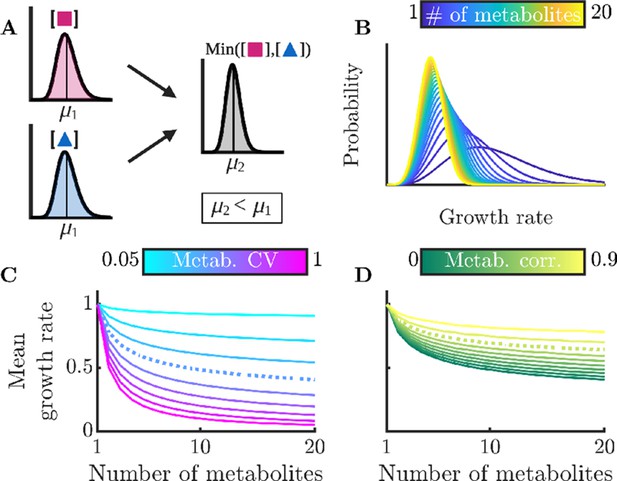
Sharing multiple metabolites can generically reduce noise and improve overall colony growth rate.
(A) Implication of Liebig’s law of the minimum for fluctuating metabolites: the growth rate at any time is set by the lowest metabolite level, hence the average growth rate is lower than at the average metabolite level. The magnitude of this decrease grows with increasing metabolite variance. (B) Distributions of growth rates, set by minimum metabolite level , for varying numbers of essential metabolites. (C) Mean growth rate as a function of number of metabolites and of metabolite CV. The dashed curve corresponds to CV =0.4, as measured for essential proteins in E. coli (Taniguchi et al., 2010). (D) Mean growth rate as a function of number of metabolites and of the correlation coefficient between metabolites, for CV=0.4. The dashed curve indicates a metabolite correlation of 0.7, approximately that observed for proteins in E. coli (Taniguchi et al., 2010).
Appendix 9—figure 1
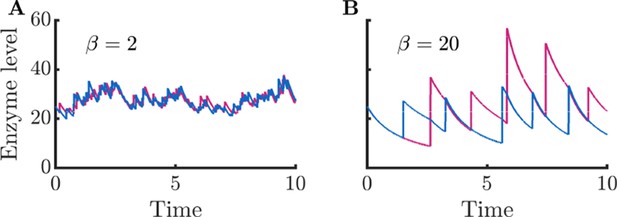
Enzyme timecourses corresponding to Figure 1CD.
(A) Enzyme timecourse of a cell that produces enzymes in small bursts, same parameters as in Figure 1C. (B) Enzyme timecourse of a cell that produces enzymes in large bursts, same parameters as in Figure 1D. Note that the enzyme levels are substantially correlated with each other ( for and for ). This correlation between enzyme levels also results in correlation between metabolite levels ( for and for ).
Appendix 9—figure 2
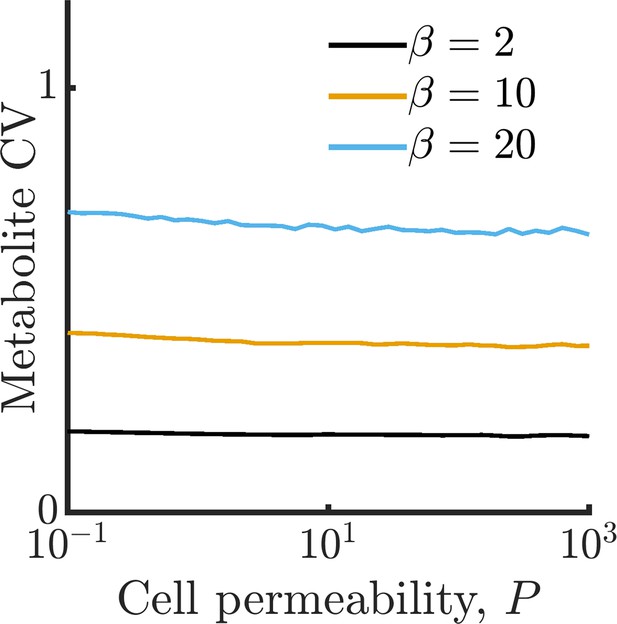
Metabolite CV corresponding to simulations in Figure 1E.
All simulation parameters identical to those in Figure 1E. Data corresponding to not shown as metabolite CV cannot be meaningfully estimated for cells with arrested metabolism.
Appendix 9—figure 3
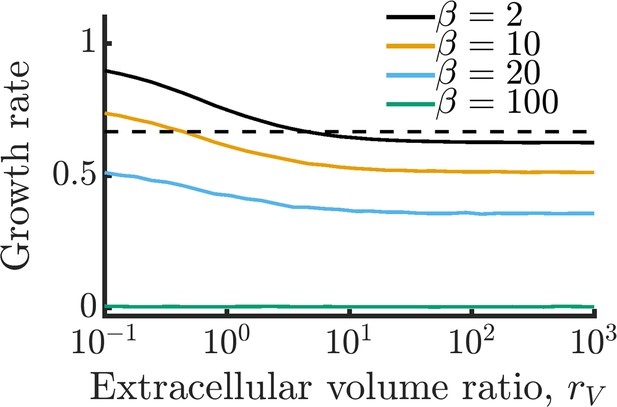
Impact of extracellular volume on growth rate of isolated cells.
As extracellular volume is increased, cells are increasingly less likely to recover their leaked metabolites, leading to decreased growth. This effect plateaus once the extracellular volume becomes effectively infinite such that cells never recover their leaked metabolites. The dashed black line represents the maximum growth rate of cells at infinite volume, calculated by treating the permeability as an additional intracellular metabolite degradation term (i.e. ). Parameters used are the same as in 1E with a permeability of . Values presented are averaged from 100 replicate simulations.
Appendix 9—figure 4
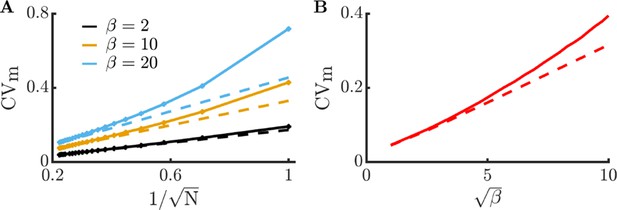
Comparison of Langevin equation predictions to full metabolism model.
The full model is simulated with the same parameters as in Figure 1EF, except with and . We apply the following substitutions to the Langevin model in order to directly compare it to the full model: , , and , where . (A) Comparison of metabolite CV in the full model (solid curves) and the Langevin model (dashed curves) as a function of community size at different burst sizes. (B) Comparison of metabolite CV in the full model (solid curve) and the Langevin model (dashed curve) as a function of burst size. As expected, the agreement between the full model and the Langevin model is best at high and low - conditions that lead to low levels of noise.
Appendix 9—figure 5
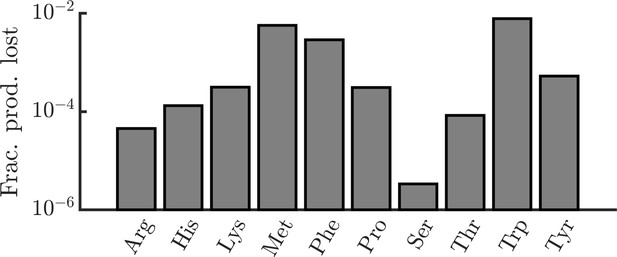
Estimated fractional production losses of amino acids in E. coli due to leakage.
E. coli due to leakage. In order to determine the significance of amino-acid leakage in E. coli, we estimated the fraction of E. coli’s amino-acid production that is lost to leakage. Formally, we define the fraction of production lost as the ratio of the number of amino acids lost via leakage over the period of one division to the number of amino acids required to produce a daughter cell. For each amino acid, we require three experimentally measured quantities for this calculation: (1) the rate of leakage through the cell membrane, (2) the intracellular concentration of the amino acid, and (3) the number of amino acids required to produce a daughter cell. For leakage rates, we use data from artificial liposomes (Chakrabarti and Deamer, 1992). In cases where multiple pH conditions were tested, we used data measured at pH 7 (though leakage rates did not vary substantially with pH). This study measured data for only a limited set of amino acids. For other amino acids, we estimated their leakage rates using a linear regression of leakage rate versus log octanol/water partition coefficient (). Leakage rates were also adjusted for the differing size of the liposomes and typical E. coli cells, assuming a liposome radius of 100 nm and an E. coli radius of 400 nm (Grossman et al., 1982). Intracellular concentrations were taken from (Bennett et al., 2009) and per-cell pool sizes were calculated assuming a cell volume of (Outten and O’Halloran, 2001). A cell’s amino-acid production was assumed to be the number of amino acids required to produce a daughter cell, taken from (Mee et al., 2014). With all of these experimental values, the fraction of production lost is where is the leakage rate, is the intracellular molecule count, is the doubling time (assumed to be 24 minutes), and is the number of amino acids required to produce a daughter cell.
Appendix 9—figure 6
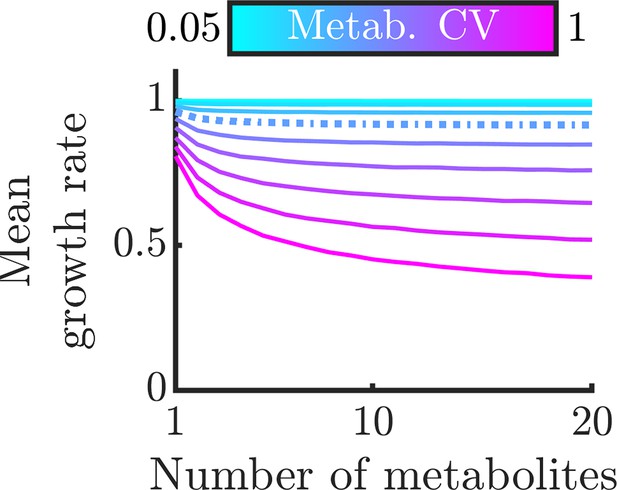
Version of Figure 3C with an alternative growth function.
To demonstrate that our findings are not limited to Liebig’s law of the minimum, we repeat the analysis in Figure 3C with an alternative growth function from (Goyal and Wingreen, 2007). The function is , where is the maximum growth rate, is the total number of unique metabolites, and is the half-substrate constant of each metabolite. In this analysis we assume and .
Appendix 9—figure 7
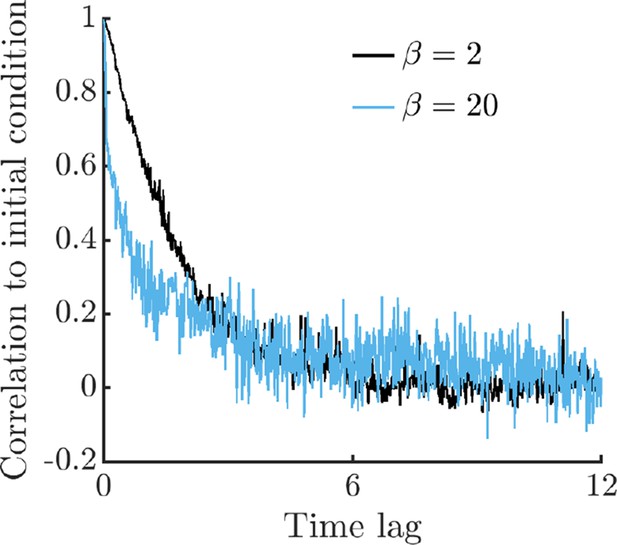
Correlation between initial conditions and later times in the full metabolism model.
To compute correlations to the initial condition, we perform 2,500 replicate simulations of single-cell metabolism with two different values of burst size , each with the same initial conditions except for the value of E1, which is uniformly distributed in the range . Simulations are run for 12.5 time units, where time is normalized to the maximum steady-state growth rate, as in Figure 1. We bin the resulting timeseries with a window size of 0.025 time units, computing Pearson correlations between the initial conditions and all data points within the window. From each bin, we also compute the mean time of datapoints within the bin, which we use as the -axis data in this figure. As can be seen, the system rapidly forgets its initial conditions, nearing zero correlation after a short time lag.
Appendix 9—figure 8
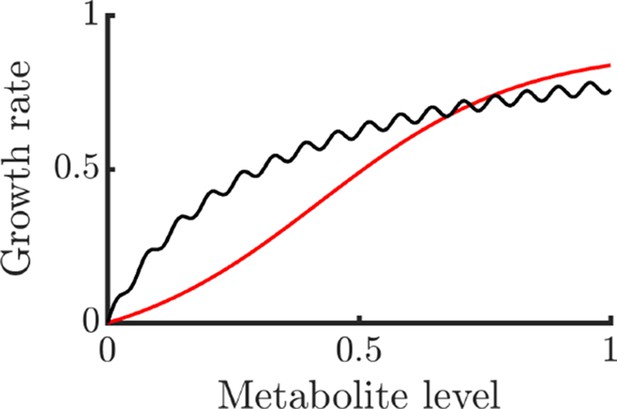
Examples of non-globally concave growth functions that still allow NAC to be potentially beneficial.
The black curve is and the red curve is . For metabolites uniformly distributed in the domain , both functions have negative Jensen gaps and are thus negatively impacted by noise.
Appendix 9—figure 9
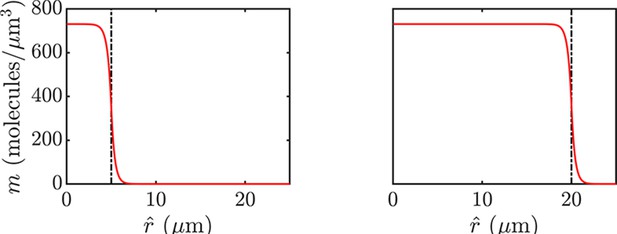
Spatial profiles of NAC metabolites within a biofilm.
Here, we plot solutions of the biofilm model analyzed and parameterized in Appendix 7. The dashed lines represent the boundary between the NAC and non-NAC sectors of the biofilm, with the NAC sector beginning at . Left: Metabolite profiles with a NAC sector of radius . Right: Metabolite profiles with a NAC sector of radius .
Appendix 9—figure 10
Analysis of metabolism model without metabolite degradation.
(A–B) Versions of Figure 1EF with . Panel A shows an extended range of permeability values to show the non-monotonic growth behavior. Data in A is computed from 100 replicates and the data from B is computed from 200 replicates. All parameters identical to the original figure with the exception of the degradation rate, . Simulations are initialized with zero extracellular metabolites. (C–D) Timecourses of metabolite and enzyme levels in an isolated cell exhibiting build-up and crash behavior. Parameters the same as in Figure 1D with the exception of and . Time normalized by inverse of maximum steady-state growth rate. (E–F) Versions of Figure 2BC with . Data is computed from 40 replicates. All parameters identical to the original figure with the exception of the degradation rate, . Simulations are initialized with zero extracellular metabolites.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Noisy metabolism can promote microbial cross-feeding
eLife 11:e70694.
https://doi.org/10.7554/eLife.70694
