Particle foraging strategies promote microbial diversity in marine environments
- Ralph M. Parsons Laboratory for Environmental Science and Engineering, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, United States
- Physics of Living Systems, Department of Physics, Massachusetts Institute of Technology, United States
Figures
Figure 1 with 1 supplement
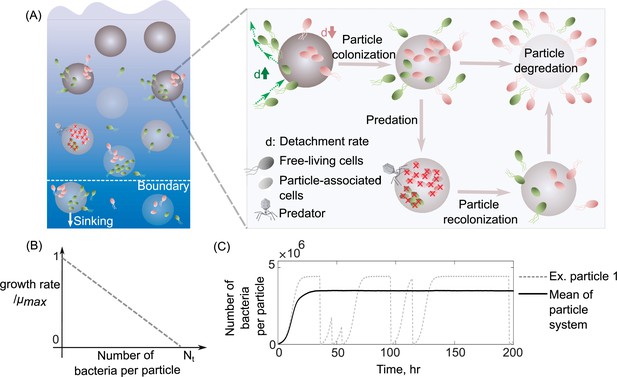
Schematic representation of the mathematical model simulating slow and fast dispersal strategies of bacterial populations that colonize particulate organic matter.
(A) The model assumes that the predation on a particle or sinking out of system’s boundaries kills its all associated populations. After infection, the noncolonized particle is then recolonized by free-living populations. As resources on a particle are consumed, its associated populations are dispersed and are added to the free-living populations. In this case, the old particle is replaced by a new uncolonized particle in the system. (B) The growth kinetics on a single particle is assumed to be density dependent and decreases linearly as a function of the number of cells colonizing the particle. Nt represents the carrying capacity of the particle. (C) The dynamics of particle-associated cells and their corresponding growth rates are shown for a system with 1000 particles. The mean values over many particles and an example of dynamics on a single particle are illustrated.
Figure 1—figure supplement 1
Bacteria-particle encounter probability.
(A) Encounter probability of a bacterial cell and a particle as a function of cell–particle distance, Dc,p. An analytical model based on the hitting probability of two objects from random walk theory is used to obtain the encounter probability (Equation 5). Bacterial cell and particle sizes are assumed to be 1 and 100 µm, respectively. Simulations are performed for two time intervals of 1 and 10 s. (B) The rate of free-living bacterial cells attachment to particles as a function of time for various number particle availability in the environment.
Figure 2 with 5 supplements
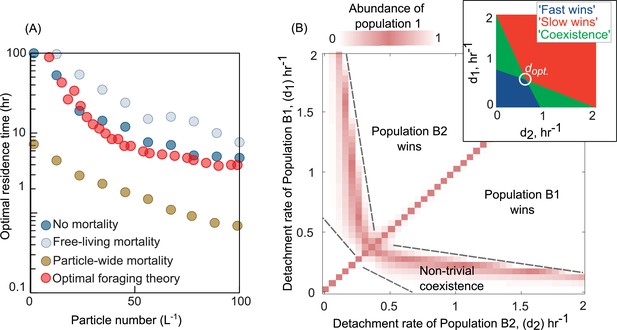
Variation in bacterial detachment strategies allow coexistence in the particle system.
(A) Optimal residence time predicted by the population-based model and optimal foraging theory (OFT; Methods). Three scenarios with various particle-wide mortality (mp) and mortality on free-living populations (mF) are simulated with the following rates: (1) particle-wide mortality (mp = 0.05 hr−1, mF = 0.02 hr−1), (2) free-living mortality (mp = 0 hr−1, mF = 0.05 hr−1), and (3) no mortality (mp = 0 hr−1, mF = 0 hr−1). To calculate optimal residence time based on OFT, we used our model and tracked individual cells attaching to a particle. The time-averaged uptake rate of the attached cell and its instantaneous uptake rate were calculated. The residence time with similar instantaneous and time-averaged uptake rates is assumed to be optimal residence time based on OFT (see Method for details). In our population-based model, the optimal residence time is assumed to be a residence time that maximizes the growth return from the particles. (B) The relative abundance of population 1 is shown for competition experiments of two populations with different detachment rates. The relative abundance is measured at the equilibrium, where no changes in the sizes of both populations are observed. The area with white color represents the conditions where either one of the populations is extinct. The mortality on particles is assumed 0.02 hr−1. (inset) Phase diagram of the coexistence as a function of detachment rates for two competing populations. dopt represents the optimal detachment rate that the coexistence range nears zero. (B) The attachment rates are kept constant at 0.0005 hr−1. The number of particles is assumed to be 60 L−1. The carrying capacity of the particle is assumed to be 5e106. Simulations are performed using our population-based mathematical model.
Figure 2—figure supplement 1
Two examples of population dynamics are shown wherein both populations reach a stable coexistence (I), while in the other scenario (II), one population is extinct.
The detachment rates of the populations B1 and B2 in scenarios I and II are (0.7 hr−1, 0.2 hr−1) and (0.7 hr−1, 1 hr−1), respectively. These population dynamics correspond to the conditions simulated in Figure 2B.
Figure 2—figure supplement 2
The relative abundance of population 1 is shown when no mortality on particles is considered for competition experiments of two populations with different detachment rates.
The parameters for the simulations are selected similar to Figure 2A, except with no particle-wide mortality.
Figure 2—figure supplement 3
In the absence of environmental fluctuations, competition experiment between populations with different detachment rates shows an emergence of an optimal detachment strategy that outcompete other populations.
The relative abundances of populations with different detachment rates are shown over time. The simulations start with 100 populations with the same relative abundances that they only differ in their detachment rates. In this simulation, bacterial cells colonize 1000 particles with a constant attachment rate (~0.0005 hr−1). Two mortality rates are simulated (low: 0.04 hr−1 and high 0.08 hr−1).
Figure 2—figure supplement 4
Cooperative growth kinetics restricts the coexistence range among two populations with different dispersal strategies.
(A) Schematic representation of various growth kinetics on particles as a function of the number of bacteria on particles. (B) The coexistence range among two populations is shown as a function of the detachment rate of the second population. The coexistence range represents a range of detachment rates for both populations that coexist at the equilibrium. Inset panel represents the relative abundance of population 1 for different detachment rates. Detachment rates with relative abundances less than 5% is assumed extinct. The mortality on particles is assumed 0.02 hr−1. The attachment rates are kept constant at 0.0005 hr−1. The number of particles is assumed to be 60 L–1. The carrying capacity and maximum growth rates are assumed, Nt = 5 × 106 and µmax = 0.50 hr−1, respectively.
Figure 2—figure supplement 5
The sensitivity of coexistence among bacterial detachment strategies to competitive growth kinetic parameterizations (Equation 6: maximum growth rate μmax and carrying capacity, Nt).
The relative abundance of population 1 is shown for competition experiments of two populations with different detachment rates and for two different values of maximum growth rates and carrying capacities. The area with white color represents the conditions where either one of the populations is extinct. The mortality on particles is assumed 0.02 hr−1. The attachment rates are kept constant at 0.0005 hr−1. The number of particles is assumed to be 60 L–1.
Figure 3
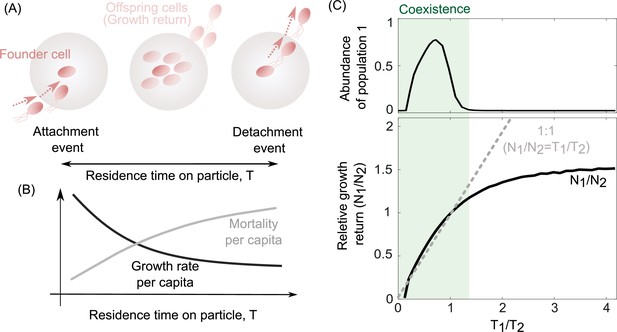
The trade-off between bacterial growth return and survival on the particles determines the coexistence range of competing populations.
(A) The growth return of a single cell on a particle is calculated based on the number of offsprings produced during a single attachment/detachment event. (B) The growth rate on particles slows down as the particle is populated by offspring cells or new attaching cells that limit the net growth return from a particle. (C) The ratio of growth returns and survival of populations 1–2 per capita as a function of their radios of residence times is shown. The residence time on the particle is assumed to be the inverse of each population’s detachment rate. The relative abundance of population 1 is shown for its corresponding simulations. The data are shown for the simulations where detachment rate of population 2 was kept constant at 0.2 hr−1. Constant residence time for the population 2 (4 hr) is considered while varying the residence time of the first population across simulations. 1:1 line represents a coarse-grained model for the coexistence criteria of two competing populations.
Figure 4 with 2 supplements
Particle abundance and predation rate shape the coexistence of populations with different dispersal strategies on the particle system.
(A) The coexistence probability is shown for a range of particle abundances and predation rates. The coexistence probability is calculated by performing multiple competition experiments across populations with various detachment rates and quantifying the number of conditions that the coexistence between two populations is found. (B) For three particle abundances in A, the relative abundance of population 1 is shown in competition experiments of two populations. The numbers in circles refer to conditions in A. Simulations are assumed to be at the equilibrium when no changes in the size of either population are observed. The area with white color represents the conditions where either one of the populations is extinct. (C) A sine function is introduced to represent particle abundance fluctuations. (D) The coexistence range represents a range of detachment rates for populations that coexist at the equilibrium. Populations with relative abundances less than 5% of the most abundant population is assumed extinct. (E) The coexistence range is shown as a function of particle fluctuation period. The attachment rate and mortality rates are assumed to be ~0.0005 and ~0.045 hr−1.
Figure 4—figure supplement 1
Particle abundance distributions extracted from the field observations.
The particle abundances are extracted over many field observations across many aquatic environments at different geographical locations (Möller, 2012; Ashjian et al., 2005; Gallager et al., 2004; Norrbin et al., 1996). The mean particle abundance over these field data is approximately 25 per liter.
Figure 4—figure supplement 2
The durations of environmental fluctuation periods for particle abundances are extracted from field data Lampitt et al., 1993.
(A) The fluctuations in particle abundance are characterized by quantifying fluctuation periods from the time difference between two neighboring local minimum and maximum, as illustrated in the schematic. (B) Probability distribution functions for fluctuation periods in particle abundances obtained from field observations.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Particle foraging strategies promote microbial diversity in marine environments
eLife 11:e73948.
https://doi.org/10.7554/eLife.73948
