Figures and data in Hydrodynamic model of fish orientation in a channel flow

Figures
Tables
Additional files

8 figures, 4 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

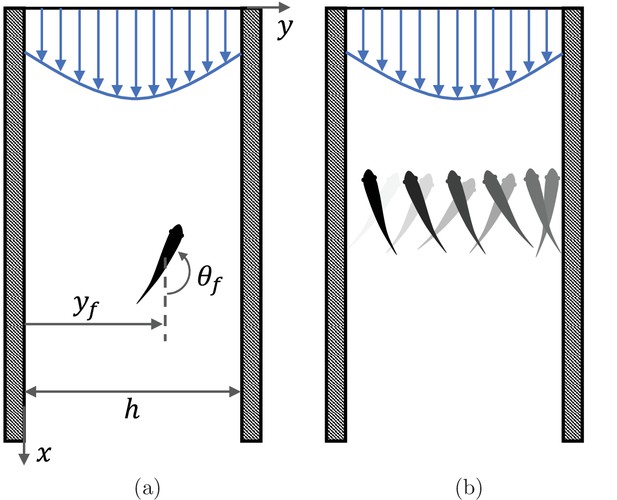
Fish rheotaxis.

(a) Illustration of the problem with notation, showing a fish swimming in a background flow described by Equation 4. (b) Schematic of the cross-stream sweeping movement of some fish species swimming without visual cues; snapshots of fish at earlier time instants are illustrated by lighter shading.

Figure 2

Download asset Open asset

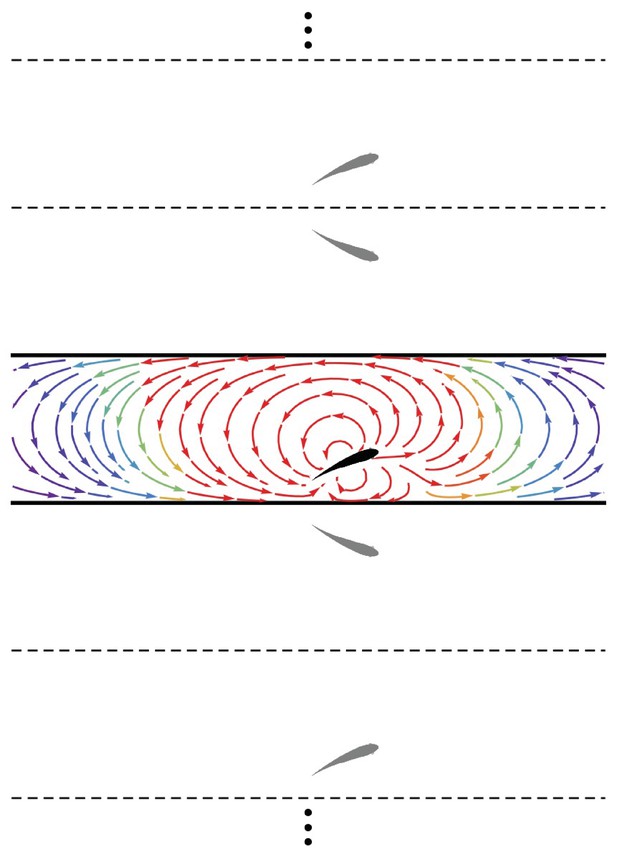
Method of images.

Schematic of the fish (black) in the channel (thick lines) and the set of images (gray) needed to generate the channel. The streamlines generated by the fish in an otherwise quiescent fluid are shown in the channel colored by local velocity magnitude (red: high; blue: low). Dashed and solid lines are mirroring planes for the method of images, the pattern for which continues *ad infinitum*.

Figure 3

Download asset Open asset

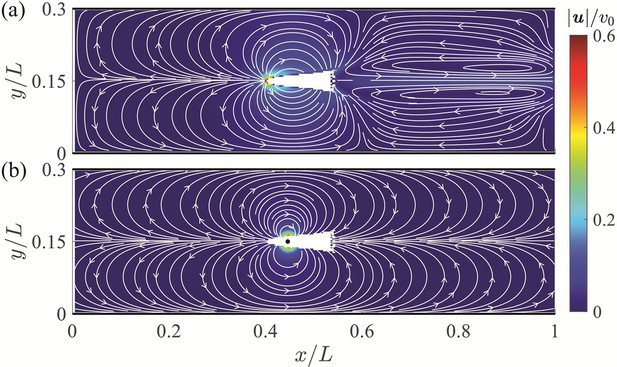
Velocity field around a swimming fish from computational fluid dynamics.

(a) Mean velocity field around the steady swimming giant danio relative to the background flow. (b) Velocity field predicted by a dipole with $θ = π$ located at $0.315 l$ from the fish head along its centerline relative to the background flow. The selection of the dipole location and strength is detailed in Appendix 2.

Figure 4

Download asset Open asset

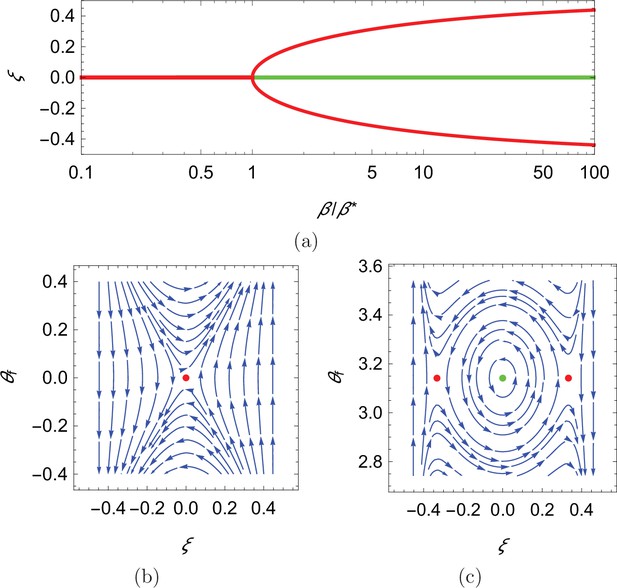
Qualitative dynamics of equation set Equation 10a.

(a) Cross-stream equilibria for upstream swimming as a function of β. (**b,c**) Phase plot for downstream and upstream swimming in the case $α = 0.1$ , $ρ = 0.1$ , and $κ = 1$ , so that $β = 20$ . In all panels, red refers to unstable equilibria and green to stable equilibria.

Figure 5

Download asset Open asset

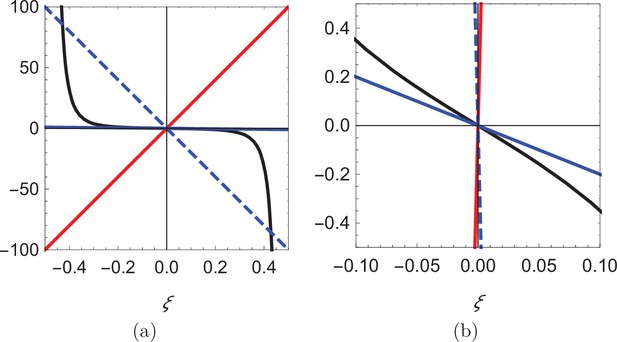
Visual illustration of the process of determining the roots of Equation 14.

(a) Plot of the function $\frac{π^{3}}{32} \cot (π (ξ + \frac{1}{2})) \csc^{2} (π (ξ + \frac{1}{2}))$ (black), superimposed with three lines of different slope: 200 (red), -200 (dashed blue), and -2 (solid blue). (b) Zoomed-in view of the curves in (a) showing that the blue line can only intersect the black curve at the origin.

Appendix 2—figure 1

Download asset Open asset

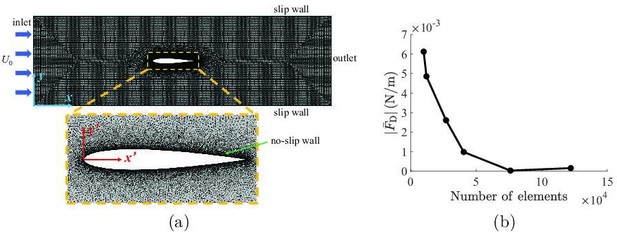
Details about the implementation of the computational fluid dynamics simulations.

(a) Mesh implemented in the simulations, with definitions of coordinate systems and a zoomed-in view of the refined mesh around the fish. (b) Mesh convergence analysis, showing the mean drag as a function of number of elements in the simulation.

Appendix 2—figure 2

Download asset Open asset

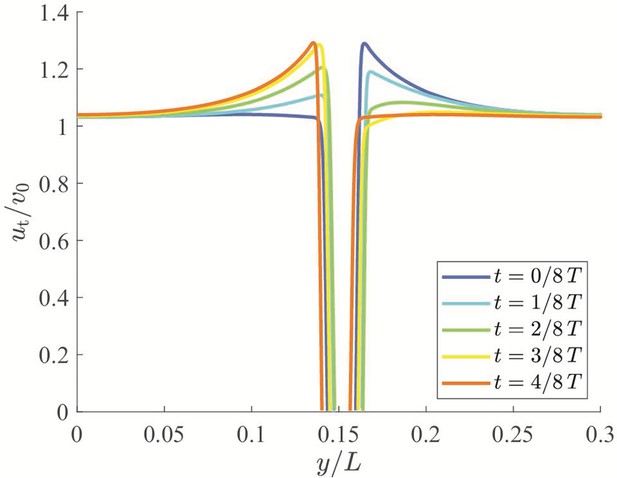
Instantaneous velocity fields around a swimming fish relative to the background flow from computational fluid dynamics.

(a) – (e) correspond to $t = 0$ , $T / 8$ , $T / 4$ , $3 T / 8$ , and $T / 2$ , respectively, where $T$ is the period of a tail beat. White curves are streamlines with arrows indicating flow directions.

Appendix 2—figure 3

Download asset Open asset

Analysis of the boundary layer thickness along a swimming fish.

x-component of the flow velocity, $u_{t}$ , extracted across the half-length of the fish body. The values of $u_{t}$ are measured in a coordinate system moving at the speed of v₀ along the fish swimming direction.

Tables

Table 1

Estimation of model parameters from data in the literature.

Reference	$ρ$	$ϵ$	$α$	$κ$	$β$
Bak-Coleman et al., 2013	$\sim 0.05$	$[10^{- 2}, 10^{- 1}]$	$[0, 0.17]$	—	—
Bak-Coleman and Coombs, 2014	$\sim 0.04$	$[10^{- 2}, 10^{- 1}]$	$[0, 0.16]$	$\sim 0$	$[0, 100]$
Baker and Montgomery, 1999 and Montgomery et al., 1997	$\sim 0.1$	$[10^{- 2}, 10^{- 1}]$	$^{*} [0, 0.32]$	$[2, 7]$	$[0, 256]$
Elder and Coombs, 2015	$\sim 0.066$	$[10^{- 2}, 10^{- 1}]$	$^{*} [0, 0.24]$	$\sim 0$	$[0, 55]$
Kulpa et al., 2015	$\sim 0.04$	$\sim 1$ near center of jet	$\sim 1.3$	—	—
Oteiza et al., 2017	$[0.018, 0.066]$	$[0.20, 0.82]$	—	—	—
Peimani et al., 2017	$\sim 0.044$	$\sim 1$	—	—	—
Suli et al., 2012	$\sim 0.018$	$[0.1, 1]$	—	—	—
Van Trump and McHenry, 2013	$[0.055, 0.127]$	$[10^{- 2}, 10^{- 1}]$	$^{*} [0, 0.32]$	$\sim 0$	$[0, 106]$

LL+ cavefish swimming speed $v_{0} \sim 5 c m / s$ in zero background flow in Bak-Coleman and Coombs, 2014 is used to estimate α.

Appendix 2—table 1

Parameters employed in (27) to describe the locomotory pattern of a giant danio.

Parameters	$l$	$c_{1}$	$c_{2}$	$k_{L}$	$f$
Values	$7.3 cm$	0.004	$- 2.33 m^{- 1}$	$78.5 m^{- 1}$	$3 Hz$

Appendix 3—table 1

Relevant publications on fish rheotaxis in the absence of visual cues, identified through literature review.

Reference	Fish		Swimming domain	Flow properties		*Sensory cues	Rheotaxis threshold speed
Reference	Species	Length	Swimming domain	Flow speed	Flow gradient	*Sensory cues	Rheotaxis threshold speed
Bak-Coleman et al., 2013	Giant danio (Devario aequipinnatus)	6.0 –7.3 cm	Flow tank of $25 \times 25 \times 25 c m$ ( $L \times h \times W$ )	0, 3, and $7 cm / s$	$Re \sim 7500$ at LL+ threshold speed; flow gradient expected to be small near center of tank	LL+/LL-	$\leq 3 cm / s$
Bak-Coleman and Coombs, 2014	blind cavefish (Astyanax mexicanus)	4.2 –5.0 cm	Flow tank of $25 \times 25 \times 25 c m$ ( $L \times h \times W$ )	0, 1, 2, 3, 4, 7 and $8 cm / s$	$Re \sim 2000$ at LL+ threshold speed; flow gradient expected to be small near center of tank	LL+/LL-; fish made transient contacts with substrate	LL+: $0.90 c m / s$ ; LL-: $0.54 c m / s$
^†Baker and Montgomery, 1999	blind cavefish (Astyanax fasciatus)	4 –7 cm	Flow tank of $51 \times 9 \times 20 c m$ ( $L \times h \times W$ )	0, 2, 3, 5, 9 and $16 cm / s$	$Re \sim 2000$ at LL+ threshold speed; flow gradient expected to be small near center of tank	LL+/LL-; tactile senses	LL+: 2– $3 cm / s$ ; LL-: 9– $16 cm / s$
Elder and Coombs, 2015	Mexican tetras (Astyanax mexicanus)	$8.3 cm$	Flow tank of $25 \times 25 \times 25 c m$ ( $L \times h \times W$ )	0, 1, 2, 4, 7, and $12 cm / s$	$Re \sim 5000$ at threshold speed; flow gradient expected to be small near center of tank	LL+/LL-	$\sim 2 cm / s$ for LL+ and LL-
Kulpa et al., 2015	blind cavefish (Astyanax mexicanus)	4.4 –5.3 cm	Flow tank of $25 \times 25 \times 10 c m$ ( $L \times h \times W$ )	Maximum speed of $8 cm / s$	Jet flow across center of tank; flow gradient expected to be large	LL+/LL-	$\leq 8 cm / s$
^‡Lyon, 1904	blind Fundulus	unspecified	Trough with unspecified dimensions; tideway leading to pond	“not too strong current” in trough and current with “more or less eddy and irregularity” in tideway	Flow gradient expected to be small	LL+; some fish gained tactile senses	Not measured; rheotaxis elicited only by tactile cues
^‡Lyon, 1904	blind Fundulus	unspecified	Trough with unspecified dimensions	flow “gushing rather violently”	Jet flow; flow gradient expected to be large	LL+	Not measured; rheotaxis elicited by flow
^†Montgomery et al., 1997	blind cavefish (Astyanax fasciatus)	4 –7 cm	^§Flow tank of $51 \times 9 \times 20 c m$ ( $L \times h \times W$ )	0, 2, 3, 5, 9, and $16 cm / s$	$Re \sim 2000$ at LL+ threshold speed; flow gradient expected to be small near center of tank	LL+/LL-; tactile senses	LL+: 2–3 cm/s; LL-: 9–16 cm/s
Oteiza et al., 2017	zebrafish (Danio rerio) larva 5–7 days post fertilization (dpf)	unspecified	13 cm-long circular tube with diameter 1.27– $4.76 c m$	0.2–0.8 cm/s	Low to high flow gradients identified through particle image velocimetry	LL+/LL-	LL+: rheotaxis observed as low as $0.2 cm / s$
Peimani et al., 2017	zebrafish (Danio rerio) larva 5–7 dpf	estimated $\sim 0.35 c m$	Flow channel of $63.3 \times 1.6 \times 0.55 m m$ ( $L \times h \times W$ )	0.95–3.8 cm/s	$Re \sim 10$ at threshold speed; flow gradient expected to be large	LL+	$0.95 cm / s$
Suli et al., 2012	zebrafish (Danio rerio) larva 5 dpf	$\sim 0.33 cm$	Flume of $110 \times 3.7 \times 2.8 c m$ ( $L \times h \times W$ )	0.075, 0.15, $0.2 cm / s$	$R e < 75$ ; flow gradient expected to be large	LL+/LL-	Not quantified
Van Trump and McHenry, 2013	blind Mexican cavefish (Astyanax fasciatus)	3 –7 cm	Cylindrical channel of $150 \times 11 c m$ ( $L \times D$ )	0, 1, 2, 4, 6, 8, 10, 13, $16 cm / s$	$R e > 2000$ at threshold speed; flow gradient expected to be small near center of tank	LL+/LL-	2–4 cm/s

*

LL+: lateral line enabled; LL−: lateral line disabled
†

Data are extracted from the same set of experiments
‡

Two experiments are considered from the same paper
§

Data are from Baker and Montgomery, 1999.

Appendix 3—table 2

Results of the bibliographical research on fish rheotaxis in the absence of visual cues, used to validate the proposed model.

Reference	Fish species	*Evidence	Comparison with model
Reference	Fish species	*Evidence	Supportive	Inconclusive
Within studies
Effect of lateral line
Bak-Coleman et al., 2013	Giant danio (Devario aequipinnatus)	No significant difference in fish heading angle against current was detected between LL+ and LL-		×
Bak-Coleman and Coombs, 2014	blind cavefish (Astyanax mexicanus)	Rheotaxis threshold speed was slightly (but not significantly) lower in LL- condition		×
Baker and Montgomery, 1999 and Montgomery et al., 1997	blind cavefish (Astyanax fasciatus)	Rheotaxis threshold speed was significantly higher in LL- condition; fish received intermittent tactile senses		×
Elder and Coombs, 2015	Mexican tetras (Astyanax mexicanus)	No significant influence of LL condition was detected on rheotactic performance		×
Kulpa et al., 2015	blind cavefish (Astyanax mexicanus)	Significantly higher rheotaxis index in LL+ fish than LL- fish in jet stream	×
Oteiza et al., 2017	zebrafish (Danio rerio) larva 5–7 dpf	Posterior lateral line ablation or chemical neuromast ablation severely reduced rheotaxis	×
Suli et al., 2012	zebrafish (Danio rerio) larva 5 dpf	LL hair cell damage led to a significant decrease in rheotaxis; regeneration of LL hair cells restored rheotaxis	×
Van Trump and McHenry, 2013	blind Mexican cavefish (Astyanax fasciatus)	In LL+ and LL-, fish exhibited statistically indistinguishable rheotaxis behavior		×
Effect of flow gradient
Lyon, 1904	blind Fundulus	In a flow with small gradient, rheotaxis was elicited only when fish received tactile cues; in jet flow with large gradient, rheotaxis was elicited by flow without tactile cues. Lack of data on statistical significance		×
Oteiza et al., 2017	zebrafish (Danio rerio) larva 5–7 dpf	Rheotaxis of fish improved with increasing gradient magnitudes	×
Across studies
Effect of channel width
Bak-Coleman and Coombs, 2014; Baker and Montgomery, 1999	blind cavefish (Astyanax mexicanus); blind cavefish (Astyanax fasciatus)	Significantly different threshold speed for LL+ fish: $0.90 \pm 0.137 cm / s$ (mean ±s.e.m.) in $25 cm$ wide tunnel; between $2 cm / s$ and $3 cm / s$ in $9 cm$ wide tunnel. Tactile cues available to fish in Bak-Coleman and Coombs, 2014		×
Bak-Coleman and Coombs, 2014; Van Trump and McHenry, 2013	blind cavefish (Astyanax mexicanus); blind cavefish (Astyanax fasciatus)	Significantly different threshold speed for LL+ fish: $0.90 \pm 0.137 cm / s$ (mean ±s.e.m.) in $25 cm$ wide tunnel; between $2 cm / s$ and $4 cm / s$ in $\sim 11 cm$ diameter tunnel. Tactile cues available to fish in Bak-Coleman and Coombs, 2014		×
Oteiza et al., 2017; Peimani et al., 2017	zebrafish (Danio rerio) larva 5–7 dpf	Onset of rheotaxis in LL+ fish observed at flow speed $0.95 cm / s$ in $1.6 mm$ wide tunnel; rheotaxis observed in LL+ fish at flow speed $0.2 cm / s$ in $2.22 cm$ diameter tunnel	×
Effect of body length
Bak-Coleman and Coombs, 2014; Elder and Coombs, 2015	blind cavefish (Astyanax mexicanus); Mexican tetras (Astyanax mexicanus)	Significantly different threshold speed for LL+ fish: $0.90 \pm 0.137 cm / s$ (mean ±s.e.m.) for 4.2– $5.0 cm$ long fish; $1.96 \pm 0.350 cm / s$ (mean ±s.e.m.) for $8.3 cm$ long fish. Tactile cues available to fish in Bak-Coleman and Coombs, 2014		×
Total			5	9

*

LL+: lateral line enabled; LL−: lateral line disabled

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/75225/elife-75225-transrepform1-v2.pdf
Download elife-75225-transrepform1-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Maurizio Porfiri
Peng Zhang
Sean D Peterson

(2022)

Hydrodynamic model of fish orientation in a channel flow

eLife 11:e75225.

https://doi.org/10.7554/eLife.75225

Share this article

Cite this article

Fish rheotaxis.

Method of images.

Velocity field around a swimming fish from computational fluid dynamics.

Qualitative dynamics of equation set Equation 10a.

Visual illustration of the process of determining the roots of Equation 14.

Details about the implementation of the computational fluid dynamics simulations.

Instantaneous velocity fields around a swimming fish relative to the background flow from computational fluid dynamics.

Analysis of the boundary layer thickness along a swimming fish.

Estimation of model parameters from data in the literature.

Parameters employed in (27) to describe the locomotory pattern of a giant danio.

Relevant publications on fish rheotaxis in the absence of visual cues, identified through literature review.

Results of the bibliographical research on fish rheotaxis in the absence of visual cues, used to validate the proposed model.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)