Measurements and simulations of microtubule growth imply strong longitudinal interactions and reveal a role for GDP on the elongating end
- Department of Biomedical Engineering, Pennsylvania State University, United States
- Departments of Biophysics and Biochemistry, The University of Texas Southwestern Medical Center, United States
Figures
Figure 1 with 4 supplements
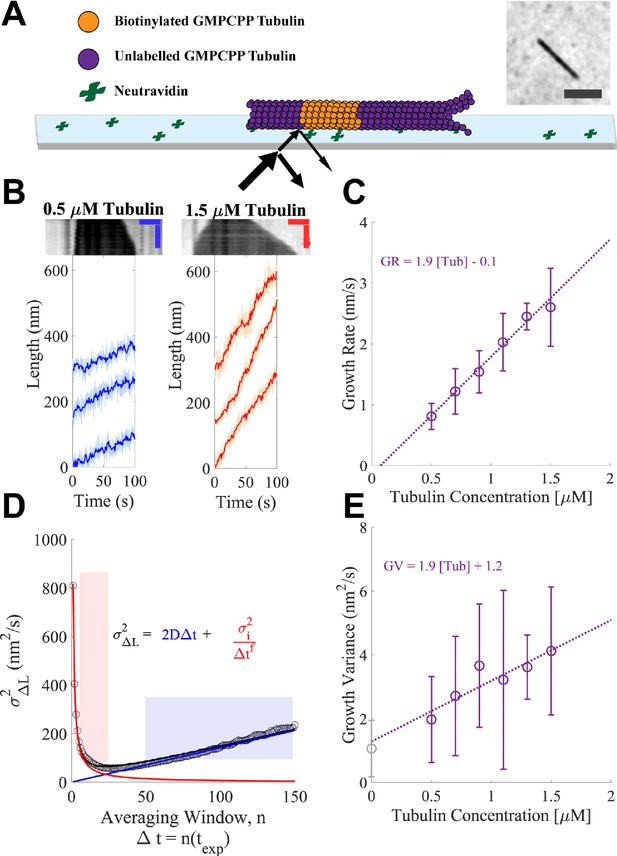
Microtubules growing in GMPCPP show slow growth and small fluctuations.
(A) Schematic of the dynamics assay. Biotinylated bovine GMPCPP microtubule seeds (orange) are attached to the cover slip through neutravidin, free unlabeled bovine tubulin is added to the flow cell in the presence of 1 mM Mg-GMPCPP, and growing microtubules are visualized using interference reflection microscopy (IRM) (image in inset; scale bar is 2 μm). (B) Example traces of microtubule plus-end growth in the presence of GMPCPP at low (blue: 0.5 μM) and high (red: 1.5 μM) tubulin concentrations. Light traces show raw end positions at 10 frames/s, and darker lines represent a 10 frame (1 s) boxcar average. Kymographs are shown above the traces. Vertical scale bar is 10 min and horizontal scale bar is 1 μm. (C) Average growth rates vs. free GMPCPP-tubulin concentration. Error bars show the standard deviation of the growth rate at each concentration (n = 21, 59, 16, 51, 9, and 23 microtubules). The dotted line shows the linear fit, weighted by the inverse of the standard error of the mean (1/SEM). (D) Measurement of the growth variance for a single microtubule. Instantaneous displacements (ΔL) are recorded over different averaging windows, where n refers to the number of frames with exposure time texp of 0.1 s averaged, and the variance of ΔL is plotted as a function of n (open black dots). The red line and shaded region show the fall in variance (approximately 1/Δt1) due to averaging out measurement error. The linear region denoted by the blue line and shading shows a crossover point where the measurement error becomes minimal and the increased variance is due to fluctuations around a mean growth rate. The black curve denotes the sum of these two phases. Reported values for growth variance in the paper refer to the ‘D’ term in the linear regime. (E) Average growth variance, resulting from fluctuations in microtubule growth, as a function of free tubulin. Error bars show the standard deviation of the measurement, and the linear fit is weighted by 1/SEM. A positive y-intercept is extrapolated back from the measurements at 1.2 nm2/s, which matches closely to our experimental noise floor measured on stationary taxol-stabilized GMPCPP microtubule seeds (gray open circle), 0.97 nm2/s.
-
Figure 1—source data 1
Source data for Figure 1C, E.
- https://cdn.elifesciences.org/articles/75931/elife-75931-fig1-data1-v2.xlsx
Figure 1—figure supplement 1
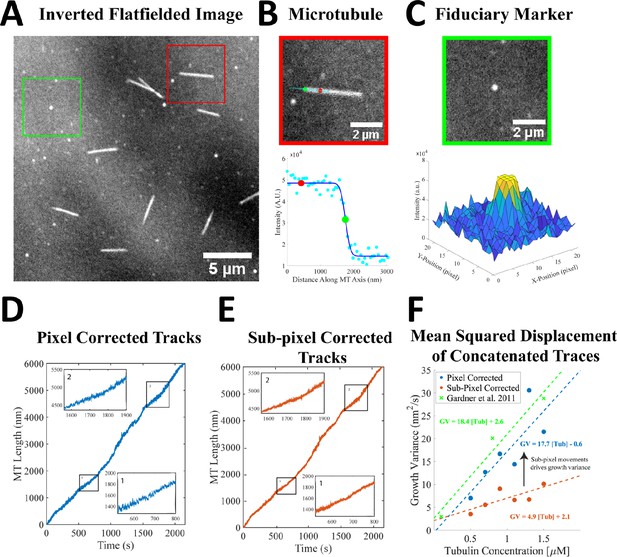
Growth variance significantly decreases with sub-pixel correction of microtubule growth.
(A) Representative interference reflection microscopy image of microtubules and fiduciary surface marks. Image is flat fielded to normalize for illumination heterogeneity, and inverted for visualization and analysis. (B) Snapshot of a growing microtubule, showing the tip tracking algorithm (Demchouk et al., 2011; Gardner et al., 2011; Prahl et al., 2014). A line (cyan) is drawn along the microtubule backbone using user-defined points (top), and the microtubule intensity along the backbone is plotted (bottom) and fit by a Gaussian survival function (dark blue line). A stationary reference point for microtubule length along the microtubule backbone is shown as a red dot in both panels, and the tip position, defined as the midpoint of the survival function, is shown by a green dot in both panels. (C) Several fiduciary marks (top panel) are used in each video to correct for sub-pixel drift during image acquisition. The fiduciary marks are fit to a Gaussian profile (bottom panel) using FIESTA (Ruhnow et al., 2011), and microtubule positions are corrected using a custom drift correction MATLAB script. (D) Concatenated traces of 13 different microtubules growing at 1.5 μM tubulin in GMPCPP, determined by the tracking algorithm developed in previous work (Demchouk et al., 2011; Gardner et al., 2011; Prahl et al., 2014). Microtubule growth was calculated as the distance between the backbone position shown (panel B, red point) and the tip position (panel B, green point). Insets 1 and 2 show small sub-pixel jumps during growth. (E) The same concatenated growth trace as panel D, following sub-pixel drift correction using several fiduciary marks. Comparison of inset regions 1 and 2 demonstrates that failing to perform sub-pixel drift correction can inflate the estimates of the fluctuations. (F) The resulting measurement of the growth variance using mean squared displacement (MSD) of the concatenated growth traces, as in Gardner et al., 2011 (red points and line). Growth variance measured before sub-pixel registration (blue points and line) matched previous results, but when sub-pixel stage movements were subtracted (orange points and line), the growth variance decreased fourfold.
-
Figure 1—figure supplement 1—source data 1
Source data for Figure 1—figure supplements 3 and 4.
- https://cdn.elifesciences.org/articles/75931/elife-75931-fig1-figsupp1-data1-v2.xlsx
Figure 1—figure supplement 2
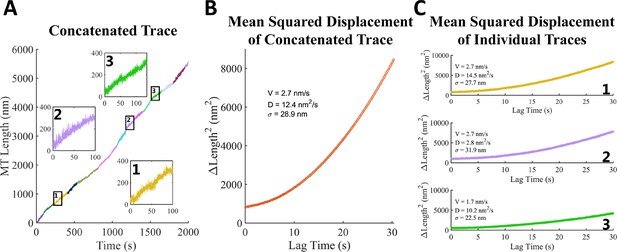
Variations between microtubules growing under identical conditions.
(A) Concatenated traces of 13 different microtubules growing at 1.5 μM free GMPCPP-tubulin. Insets show 100 s windows of different microtubules showing differences in mean velocity (2 and 3) and transient events (1 and 3) that contrast with smooth growth (trace 2). (B) Mean squared displacement (MSD) analysis of the concatenated trace shown in A, showing the fit parameters for growth rate (V), growth variance (D), and measurement error (σ). (C) MSD analysis of the individual traces shown in the insets of panel A. Note that the fit parameters for individual microtubules vary from one another and from the concatenated trace in panel B.
Figure 1—figure supplement 3
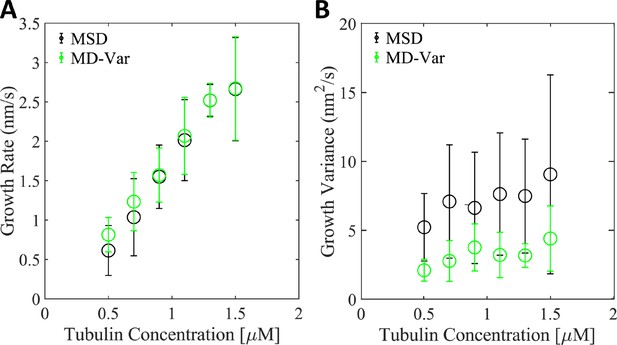
Mean displacement and variance (MD-Var) provides a better estimate for the growth variance than mean squared displacement (MSD).
(A) Average growth rate as a function of free tubulin measured by MSD (black) or by MD-Var (green); error bars show the standard deviation for the population of n = 9–59 microtubules. This comparison shows that the two approaches are in relative agreement for estimating growth rate. (B) Average growth variance as a function of free tubulin measured by MSD (black) or by MD-Var (green); error bars show the standard deviation of the population of n = 9–59 microtubules. Note that both the mean and the range of growth variance values were larger for the MSD compared to the MD-Var analysis.
Figure 1—figure supplement 4
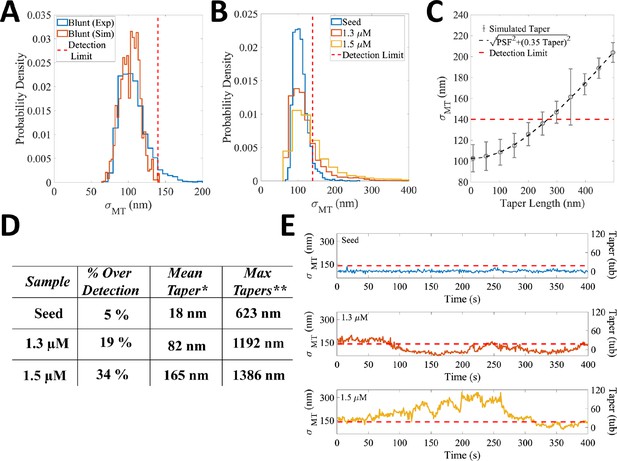
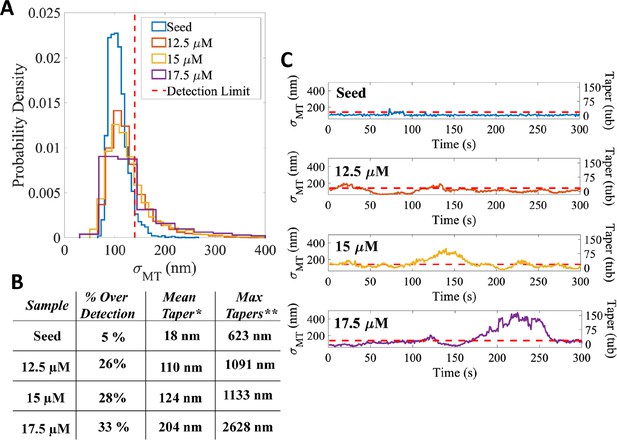
Transient tapers fluctuate around a constant value and occur more often at higher free tubulin concentrations.
(A) Tip taper sizes were estimated from the standard deviation of the survival function used to fit the fall off of intensity at the tip (σMT). To determine the minimum detectable taper, simulated images of blunt microtubules were generated by using model convolution based on our microscope setup and experimental measurement noise. The distribution of tip standard deviations from these simulated images is shown in orange. We defined the minimal experimentally detectable plus-tip taper as three times the standard deviation of this distribution (red dashed line at 140 nm). The corresponding distribution from experiments imaging blunt, taxol-stabilized GMPCPP seeds is shown in blue. Note that a small population of our blunt microtubules had σMT above the threshold; we attribute these apparent tapers to experimental noise, such as out of focus images that are not captured in the model convolution. (B) Comparison of experimentally measured tip standard deviations for taxol-stabilized GMPCPP seeds (blue), and microtubules growing in 1.3 μM free tubulin (orange) and 1.5 μM free tubulin (yellow) in the presence of GMPCPP. The detection limit of 140 nm is shown as a dotted red line. As the free tubulin concentration increased, the fraction of tip estimations above the detection limit increased. (C) Calibration curve relating tip standard deviation from the survival function fit, σMT, to the actual taper length. Model convolution was used to generate simulated images of microtubules with increasing uniform taper structures (Bohner et al., 2016; Demchouk et al., 2011; Maurer et al., 2014; Prahl et al., 2014; Ruhnow et al., 2011) where the taper length is defined as the distance between the longest and the shortest protofilament. The mean and SD of σMT for each set of images is plotted as a function of the taper length used to generate that set of images (Bohner et al., 2016; Maurer et al., 2014; Prahl et al., 2014). A theoretical relationship between σMT and taper length is calculated by adding in quadrature the standard deviation of the protofilament length, σPF, and the spread of the optical point spread function (PSF), σPSF. . The relationship between the standard deviation of the protofilament length, σPF, and taper should theoretically be , but due to increases in tracking error that occur at longer taper lengths the relationship was fit empirically using σPF = 0.35*Taper (Demchouk et al., 2011; Maurer et al., 2014). . This calibration curve was used to estimate taper length from the experimental σMT data. The threshold for a measurable taper (red dashed line at 140 nm) corresponds to a minimum detectable taper length of 265 nm. (D) Tip taper quantification on blunt microtubules and microtubules growing in GMPCPP. ‘% Over Detection’ is defined as the proportion of σMT measurements above the 140 nm detection limit defined in panel A. Note the increasing percent of measurable tips with increasing free tubulin; the 5% for the seeds represents measurement error. * ‘Mean Taper’ is calculated by converting the σMT values for each condition to taper lengths using the calibration curve in panel B, and taking the mean of this population. Note that these mean taper sizes are underestimates because any σMT below the detection limit was defined as having a taper of 0 nm. ** ‘Max Tapers’ is the average of the top 1% of tapers above the detection limit for each condition. (E) Example time courses of the spread of the survival function (σMT, left y-axis) and the corresponding estimated taper length in tubulin subunits (right y-axis) for stabilized seeds (top), and microtubules growing in 1.3 μM (middle) and 1.5 μM (bottom) free tubulin in GMPCPP. The red dotted line is the measurement detection limit. Note that for the taxol-stabilized GMPCPP seed (top panel-blue), the entire trace lies below the detection limit. The 1.3 μM free tubulin trace (middle panel – orange) shows fluctuations of the taper length occurring over 10 s of seconds. The 1.5 μM free tubulin trace (bottom panel – yellow) shows time-dependent fluctuations of taper size with a sustained period above the detection limit.
Figure 2 with 5 supplements
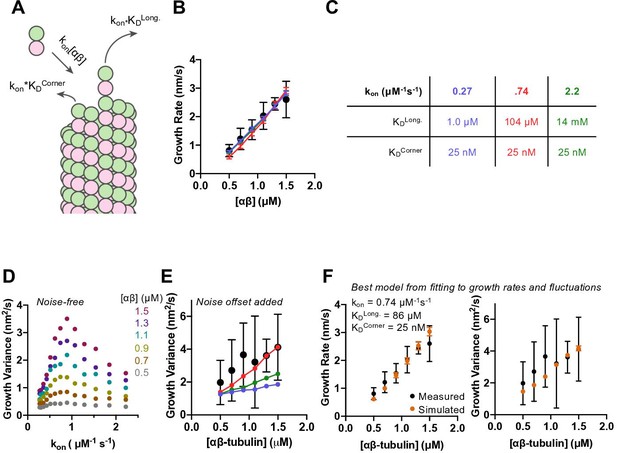
Simulations recapitulate GMPCPP growth rates for a wide range of association rates and longitudinal affinity, but fluctuations are only captured in a narrower range.
(A) Cartoon showing the dominant factors that determine the concentration-dependent growth rates: association rate is determined as kon*[αβ], where kon is the on-rate constant, and dissociation rates from longitudinal (no lateral neighbors) and corner (one lateral neighbor) sites are determined as kon*KD, where KD represents the dissociation constant for the given type of site (see Materials and methods). (B) Measured (filled circles; data from Figure 1) and simulated growth rates (lines) after fitting the model to the measurements for three different assumed kon values (blue: 0.27 μM–1 s–1, red: 0.74 μM–1 s–1, green: 2.22 μM–1 s–1). Error bars show SD (n = 50) for experimental and simulated values; when not visible, it is because the bars are obscured by the symbol. (C) Fitted parameters for the three fits depicted in B. (D) Fluctuations around the average simulated growth rate as produced by fitting the model to the measurements for a larger set of assumed kon values than in B. The magnitude of fluctuations in simulations shows a bell-shaped dependence on kon, reaching the highest values in the middle of the range explored. (E) Measured (filled black circles; data from Figure 1) and simulated (filled circles connected by lines; color coding as in B) fluctuations around the average growth rate. A ‘noise offset’ of 0.97 nm2/s (see Figure 1E) has been added to the simulation data to facilitate comparison with the measurements. Error bars are as described in (B). (F) Result of fitting the model to growth rates (left) and fluctuations (right) simultaneously. Measured values are from Figure 1 and depicted as filled circles; values from simulations are kon: 0.74 μM–1 s–1, KDlong: 86 μM, KDcorner: 25 nM. Error bars show SD (n = 50).
-
Figure 2—source data 1
Source data for Figure 2D-F.
- https://cdn.elifesciences.org/articles/75931/elife-75931-fig2-data1-v2.xlsx
Figure 2—figure supplement 1
Explanation and illustration of the model.
(A) Cartoons illustrating binding modes for αβ-tubulin (shaded oval) that differ in the number of lateral and longitudinal contacts (neighbors). The binding modes (longitudinal, top left; corner, top right) that dominate elongation rates in our model are shown in bold colors. (B) Representation of the microtubule lattice as a two-dimensional grid with a ‘wraparound’ boundary condition to model the seam. The darker rectangles represent the ‘seed’ that is used to initiate simulations. Accompanying text explains the initial conditions for starting simulations. (C) Essence of the simulation algorithm. ‘Execution times’ are computed for each possible event (association, dissociation, GTP hydrolysis), and the event with the shortest execution time is implemented, accumulated simulation time incremented, and list of possible events updated. In this way, the individual events are chosen in a way that reflects their relative probability, reflected in their different characteristic rates. (D) Explanatory cartoon illustrating the first few steps of a hypothetical simulation. (E) Simulations output the number of tubulins in the microtubule as a function of time and, if desired, the location and biochemical state of tubulins within a user-specified distance of the microtubule end. The length vs. time data can be analyzed for growth rate and fluctuations as for experimental measurements, and model parameters can be optimized to achieve the best fit to the desired experimental measurements.
Figure 2—figure supplement 2
Model fit to measured growth rates as a function of corner affinity.
The plot summarizes the result of fitting the model to the measured GMPCPP growth rates using a variety of corner affinities. The x-axis ranges from –20 to –14 kT corresponds to dissociation constants of 2 nM to 0.83 μM. For each corner affinity, the model was fit to experimental growth rates using a range of assumed kon values (see Materials and methods). Black circles represent the average goodness of fit taken over all kon values, and the boundaries of the gray shaded region show the best and worst fit obtained from an individual kon. As long as the corner affinity is sufficiently strong, the model can fit the observed growth rates. The red arrow indicates the corner affinity (–17.5 kT, corresponding to 25 nM dissociation constant) used for Figure 2F.
Figure 2—figure supplement 3
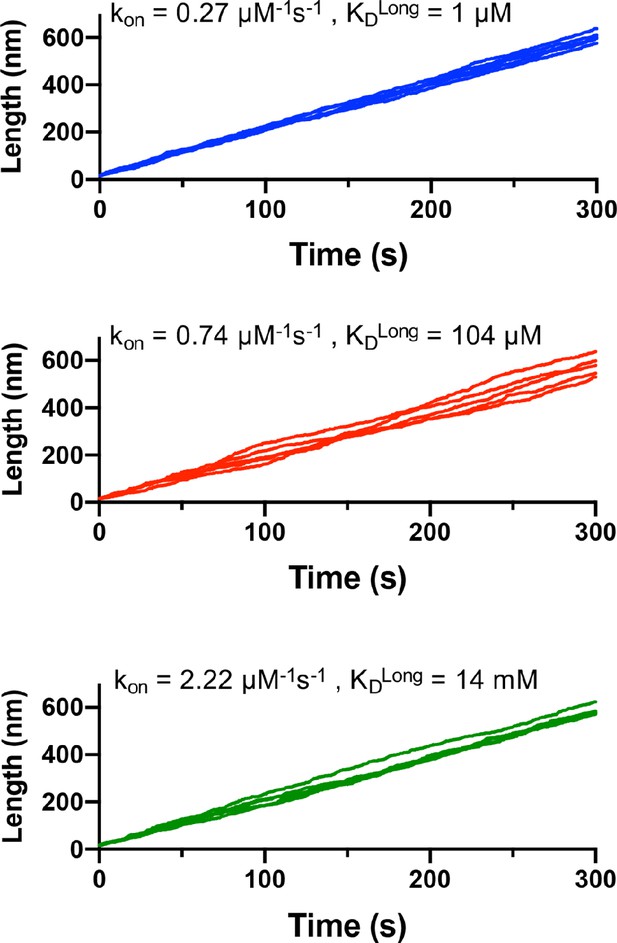
Differing magnitude variation in simulated microtubule growth at different association rate constants.
Plots of five traces of microtubule length vs. time from independent simulations are shown for three different choices of kon (0.27, 0.74, 2.22 μM–1 s–1). The different degrees of divergence in the length vs. time traces for different regimes of association rate (with their correspondingly different longitudinal affinities, see insets) reflect different magnitude variation in growth rates.
Figure 2—figure supplement 4
The taper and roughness of microtubule end structures from simulations depends on the regime of association rate and longitudinal affinity.
(Top) Representative microtubule end configurations from five independent simulations using three different choices of kon (0.27, 0.74, 2.22 μM–1 s–1). Tubulin subunits are represented as ovals, and the microtubule lattice is represented as a two-dimensional grid with protofilaments 1 and 13 at either extreme. Conditions of relatively slow association rate and strong longitudinal affinity (top row) give rise to substantial taper (difference in length of the protofilaments) and these microtubules can have multiple growth fronts. Conditions of relative fast association rate and weak longitudinal affinity (bottom row) yield blunter microtubule ends and intermediate conditions (middle row) yield slightly tapered ends with a few available growth fronts. (Bottom) Gallery of end tapers using the best fit growth parameters used in Figure 2F (kon: 0.74 μM–1 s–1, KDlong: 86 μM, KDcorner: 25 nM.) were obtained by fitting the model to both growth rates and fluctuations. Representative microtubule end configurations from 10 independent simulations are shown. Tubulin subunits are represented as ovals, and the microtubule lattice is represented as a two-dimensional grid with protofilaments 1 and 13 at either extreme. End configurations here varied from more blunt ends to longer tapers that are several tubulin subunits long.
Figure 2—video 1
Fluctuations in microtubule growth rate and extent of end taper vary for different combinations of association rate and longitudinal affinity.
Example simulations of microtubule growth in the absence of GTP hydrolysis. Microtubule length was determined by the average length of the 13 protofilaments and discretized into 0.5 s intervals. Microtubule taper was calculated as the standard deviation of protofilament lengths. Different combinations of on-rate constant and longitudinal affinity are depicted in different colors following the same convention as Figure 2B.
Figure 3 with 1 supplement
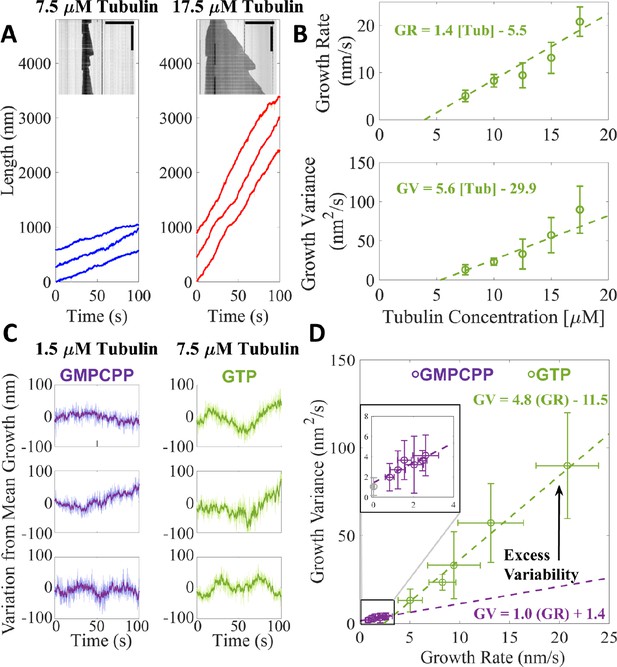
Microtubules growing in GTP show excess fluctuations compared to growth in GMPCPP.
(A) Example tracks of microtubule growth in GTP at 7.5 μM free tubulin (left, blue) and 17.5 μM free tubulin (right, red). The light shading represents the tip traces acquired at 10 frames/s and the darker traces denote a 10-frame boxcar average of the traces over time. Example kymographs of dynamic microtubules are shown as insets; horizontal scale bar is 10 μm and the vertical scale bar is 5 min. (B) Average microtubule growth rate (top) and average growth variance (bottom) as a function of free tubulin concentration in GTP. Error bars show standard deviation (n = 34, 20, 16, 15, 13 growth events). A linear fit, weighted by 1/SEM, is shown as the dashed green line. (C) Deviations from expected growth length (given by the product of the average growth rate and time) for microtubules grown in GMPCPP (left – Figure 1A) and GTP (right – A). (D) Growth variance vs. growth rate for microtubules grown in GMPCPP (purple) and GTP (green). Error bars are SD. The inset more clearly shows the linear relationship between growth rate and growth variance in GMPCPP (purple). The experimental noise floor is shown as the gray point in the inset. Dashed lines denote linear fits weighted by 1/SEM of the growth variance.
-
Figure 3—source data 1
Source data for Figure 3B, C.
- https://cdn.elifesciences.org/articles/75931/elife-75931-fig3-data1-v2.xlsx
Figure 3—figure supplement 1
Long transient tapers occur during microtubule growth in GTP.
(A) Distribution of measured taper sizes (σMT) of microtubules growing in GTP. Red dotted line denotes the detection limit of 140 nm. Note that as the free tubulin concentration increased, the proportion of measurements above the detection limit increased. Corresponding distributions for microtubules growing in GMPCPP are shown in Figure 1—figure supplement 4B. (B) Tip taper quantification for microtubules growing in GTP. ‘% Over Detection’ is defined as the proportion of σMT measurements above the 140 nm detection limit. Note the increasing percent of measurable tips with increasing free tubulin; the 5% for the seeds represents measurement error. * ‘Mean Taper’ is calculated by converting the σMT values for each condition to taper lengths using the calibration curve in Figure 1—figure supplement 4C, and taking the mean of this population. Note that these mean taper sizes are underestimates because any σMT below the detection limit was defined as having a taper of 0 nm. ** ‘Max Tapers’ is the average of the top 1% of tapers above the detection limit for each condition. Corresponding table for microtubules growing in GMPCPP is shown in Figure 1—figure supplement 4D. (C) Example time courses of the spread of the survival function (σMT, left y-axis) and the corresponding taper length in tubulin subunits (right y-axis) for stabilized seeds (top), and microtubules growing in increasing free tubulin concentrations in GTP. Red dotted line denotes the measurement detection limit of 140 nm. Note that episodes where the taper length exceeds the detection limit increase in both duration and magnitude with increasing tubulin.
Figure 4 with 2 supplements
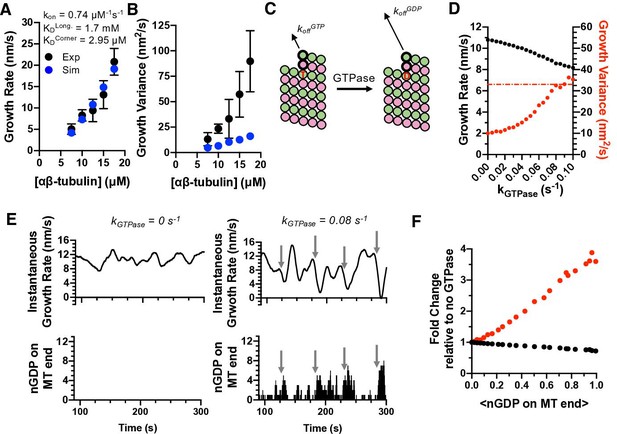
Exposure of GDP-tubulin on protofilament ends in simulations explains the excess fluctuations observed in GTP.
(A) Simulated growth rates for microtubules in GTP (blue) provide a good match to measured values (black; data from Figure 3). The GTP simulations used the optimal on-rate constant determined for GMPCPP-tubulin (kon: 0.74 μM–1 s–1; Figure 2) and used corner and longitudinal affinity values (KDcorner = 2.9 μM; KDlong = 1.7 mM) optimized to fit the experimental growth rates in GTP. Error bars show SD (n = 50) for experimental and simulated values; when not visible, it is because the bars are obscured by the symbol. (B) Fluctuations around the average growth rates in simulations (blue) substantially underestimate the measured values (black; data from Figure 3). Error bars are as in (A). (C) Cartoon illustrating how GTPase activity is incorporated into the model. Two additional parameters are required: a rate constant for GTP hydrolysis, and a scale factor to model the ‘weakening’ effect of GDP on the longitudinal interface. (D) Results from simulations at 12.5 μM αβ-tubulin (interaction strengths as in panels A and B) including GTPase activity. As the rate of GTPase increases in simulations, growth rates (black) decrease, whereas fluctuations in growth rate (red) increase to the point that they are comparable to the measured value (dotted line). (E) Exposure of GDP on the growing end of the microtubule coincides with larger fluctuations in growth rate. In the absence of GTPase (left plots), the instantaneous growth rate varies in a relatively narrow range (top) and there is no GDP exposed on the microtubule end (bottom). When GTPase activity is present (right plots), the instantaneous growth rate explores a larger range including much slower values (top), and these especially slow growth rates coincide with exposure of one or more GDP-terminated protofilaments (bottom). (F) Dependence of growth rate (black) and growth fluctuations (red) on the average number of GDP exposed on the growing microtubule end. Values are plotted as fold change relative to the no GTPase condition. Fluctuations respond more strongly to the number of exposed GDP than do growth rates.
-
Figure 4—source data 1
Source data for Figure 4A, B, D, F.
- https://cdn.elifesciences.org/articles/75931/elife-75931-fig4-data1-v2.xlsx
Figure 4—figure supplement 1
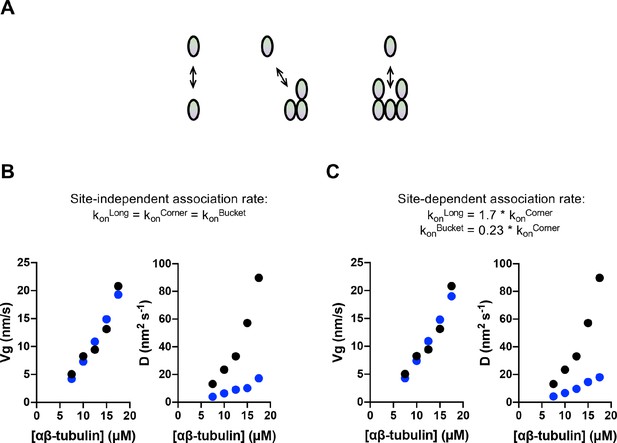
Site-dependent association rates do not explain the larger growth fluctuations observed in GTP.
(A) Cartoon of interactions occurring at the microtubule end. The interactions are ordered based on the number of lateral contacts: longitudinal (n = 0), corner (n = 1), and bucket (n = 2). (B) Comparison between measured (black) and simulated (blue) growth rates (left) and fluctuations (right). For these panels, the model used one single association rate constant for longitudinal, corner, and bucket sites. The model was fit to growth rates only. (C) Comparison between measured (black) and simulated (blue) growth rates (left) and fluctuations (right). For these panels, the model used site-dependent association rate constants for longitudinal, corner, and bucket sites. The relative factors relating the different rate constants were taken from Castle and Odde, 2013. The model was fit to growth rates only.
-
Figure 4—figure supplement 1—source data 1
Source data for Figure 4—figure supplement 1C.
- https://cdn.elifesciences.org/articles/75931/elife-75931-fig4-figsupp1-data1-v2.xlsx
Figure 4—video 1
GTP hydrolysis results in large fluctuations in microtubule growth.
Example simulations of microtubule growth in the absence (left, purple) and presence (right, green) of GTP hydrolysis. Microtubule length was determined by the average length of the 13 protofilaments and discretized into 0.5 s intervals.
Figure 5
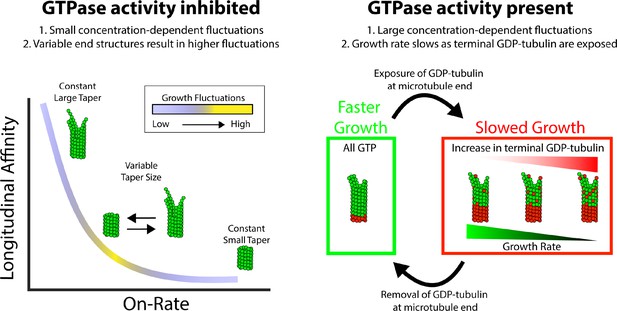
Summary of results and insights.
(Left) Microtubule growth in the absence of GTPase activity can be accounted for by a simple biochemical model that incorporates the tubulin on-rate and the longitudinal affinity of the terminal tubulin at the plus-end. A slow on-rate and strong longitudinal affinity produce small fluctuations in growth and a large taper because the protofilaments grow somewhat independently of one another. A fast on-rate and weak longitudinal affinity produce small fluctuations in growth and a small taper because only corner interactions contribute to productive growth. The middle range produces the largest fluctuations in growth rate and best matches the measured fluctuations. The reason that this regime produces the largest fluctuations is because is where the average taper is itself varying the most, which leads to episodes of faster or slower growth depending on the end configuration. (Right) When GTPase activity is present, the growth fluctuations are much larger than in GMPCPP where hydrolysis is absent. The growth rate fluctuates more drastically due to switching between fast growth phases, when all terminal tubulins contain GTP, and slow growth phases resulting from one or more exposed GDP-tubulin at the tip. When the exposed GDP-tubulin either dissociates or is buried by an incoming GTP-tubulin, an all-GTP tip with a corresponding fast growth rate is restored.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Measurements and simulations of microtubule growth imply strong longitudinal interactions and reveal a role for GDP on the elongating end
eLife 11:e75931.
https://doi.org/10.7554/eLife.75931
