Figures and data in Spontaneous neuronal oscillations in the human insula are hierarchically organized traveling waves

Figures
Additional files

7 figures and 2 additional files

Figures

Figure 1 with 2 supplements

Download asset Open asset

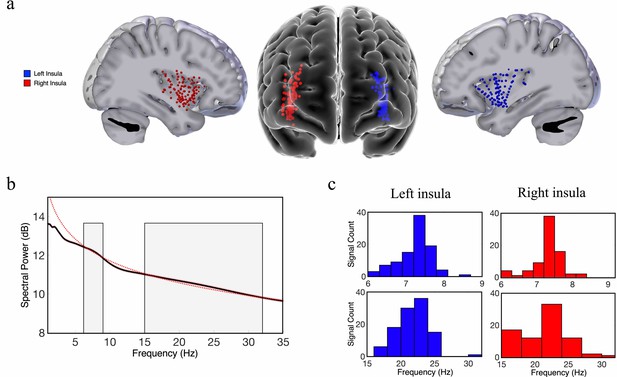
Theta-band and beta-band frequency oscillations in the human insula.

(a) Lateral and frontal views of the brain showing electrodes in the left insula (n=125) and right insula (n=114) across all participants. (b) An oscillation-detection algorithm known as multiple oscillations detection algorithm (MODAL) detected theta (~6–9 Hz) and beta (~15–32 Hz) oscillations across all electrodes in the insula (Materials and methods). The black line depicts the power spectrum, the red dotted line depicts the 1/f regression line, and the red shaded region around the spectrum represents the standard error of the mean power for each frequency. Gray shaded regions indicate the detected frequency bands at which the power spectrum was higher than the 1/f background signal. (c) The distribution of the peak frequencies detected across all insula electrodes. In the left insula, 90% of electrodes had theta oscillations and 99% had beta oscillations. In the right insula, 80% of electrodes had theta oscillations and 81% had beta oscillations. Peak frequencies of theta and beta oscillations appear to have relatively normal distributions across the insula.

Figure 1—figure supplement 1

Download asset Open asset

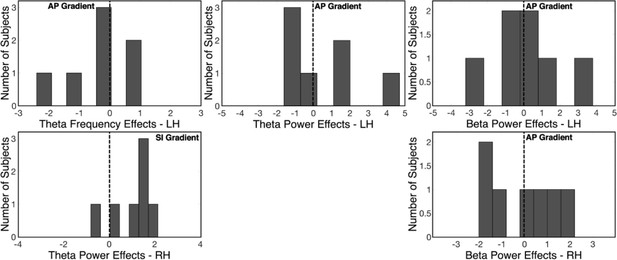
Histograms of t-statistics across subjects.

The clustering of t-scores indicates that the single-subject gradient effects directionally align with the results from the group-level statistical tests. Black vertical lines mark the center zero point, where little to no measurable effects of spatial axes on neural data were present.

Figure 1—figure supplement 2

Download asset Open asset

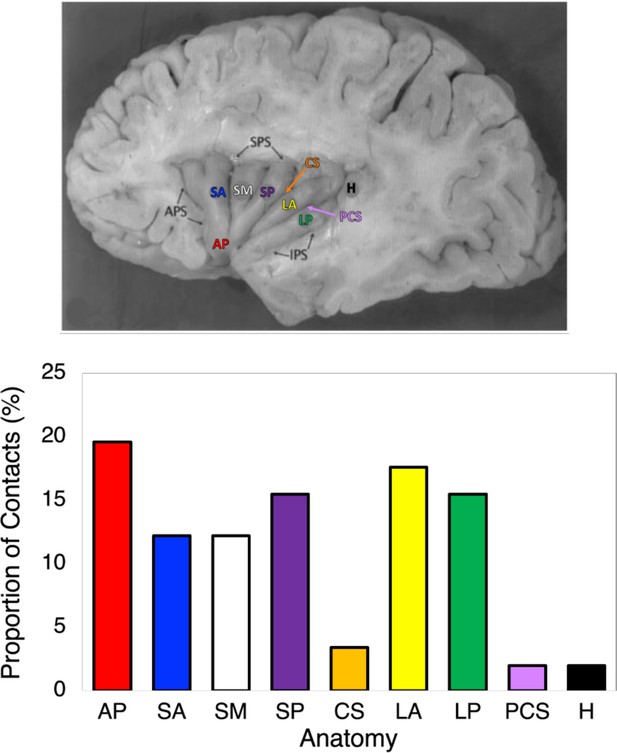
Proportion of contacts in each anatomical segment of the insula.

AP: apex; SA: short anterior gyrus; SM: short middle gyrus; SP: short posterior gyrus; CS: central sulcus; LA: long anterior gyrus; LP: long posterior gyrus; PCS: posterior central sulcus; H: Heschl’s gyrus.

Figure 2

Download asset Open asset

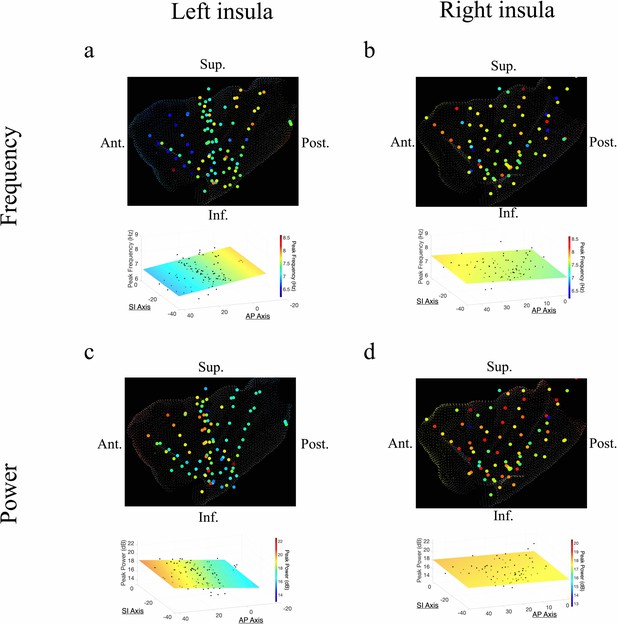
Frequency and power gradients of theta oscillations in the insula.

(a) Peak frequencies within the theta band (~6–9 Hz) showed posterior-to-anterior gradient in the left insula. Coordinates of electrodes along the AP axis predicted peak theta frequency, where slower theta frequencies were more prominent in the anterior insula and faster theta frequencies were prominent posteriorly (t[74]=–4.09, p<0.001). (b) Theta frequencies in the right insula were not hierarchically organized along the AP axis (t[57]=–0.14, p>0.05), or the superior–inferior (SI) axis (t[57]=0.07, p>0.05). (c) Theta power showed anterior-to-posterior gradient in the left insula with theta power being higher in the anterior insula (t[74]=2.52, p<0.05). (d) Theta power showed a superior-to-inferior gradient in the right insula where higher amplitude theta oscillations were prominent in the superior portion of the insula (t[57]=2.92, p<0.01). A marginally significant AP gradient suggests that theta power was slightly more concentrated in the right anterior insula, similar to the power gradient in the left hemisphere (t[57]=1.98, p=0.053). No interaction effect was observed between AP and SI axes (t[57]=–1.14, p>0.05). Results were computed using linear regression where the y-axis (AP) and z-axis (SI) electrode coordinates were used as continuous independent variables to predict spectral power and frequency dynamics. Variability across participants has been accounted for in all t-statistics. Images were generated via automatic selection of insular vertices from anatomical parcellations using the Desikan–Killiany (DK) atlas.

Figure 3

Download asset Open asset

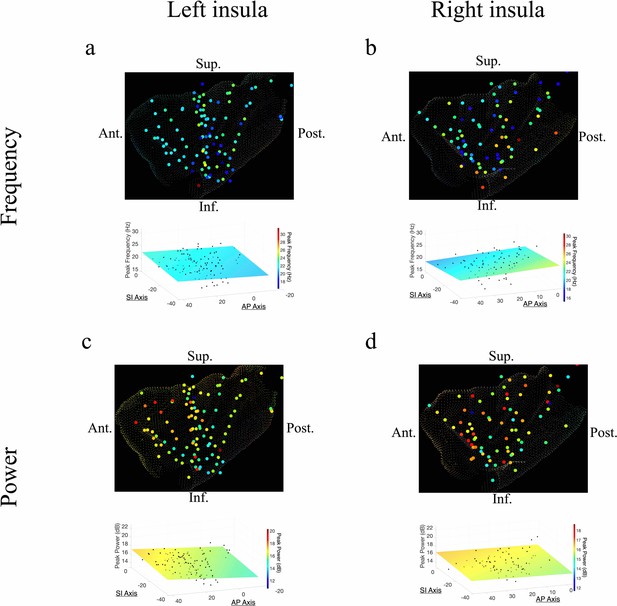
Frequency and power gradients of beta oscillations in the insula.

(a) Peak frequencies within the beta band (~15–32 Hz) showed no spatial organization in the left insula (t[84]=–0.95, p>0.05). (b) Beta frequencies in the right insula did not show AP (t[58]=–0.63, p>0.05), or SI gradients (t[58]=–1.10, p>0.05). (c) Electrode coordinates along the AP axis of the left insula predicted beta power, revealing that higher power oscillations were prominent in the anterior insula (t[84]=3.07, p<0.01). (d) Beta power in the right insula also showed an AP gradient where higher amplitude beta oscillations were prominent in the right anterior portion (t[58]=2.97, p<0.01). Results were computed using linear regression where the y-axis (AP) and z-axis (SI) electrode coordinates were used as continuous independent variables to predict spectral power and frequency dynamics. Variability across participants has been accounted for in all t-statistics. Images were generated via automatic selection of insular vertices from anatomical parcellations using the Desikan–Killiany (DK) atlas.

Figure 4 with 9 supplements

Download asset Open asset

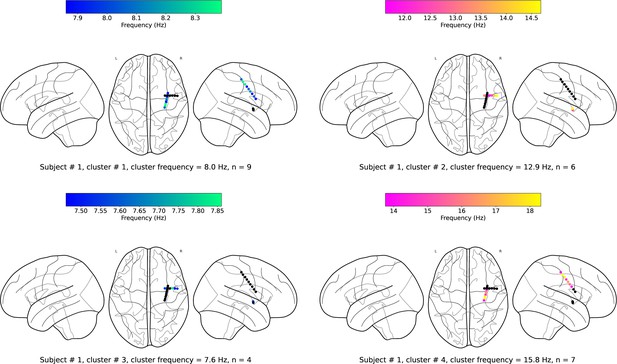
Example of spatiotemporal clustering in the human insula.

A cluster was identified as a spatially contiguous groups of electrodes that had narrowband oscillations at either theta or beta frequency band (Materials and methods). (a) Insula electrodes visualized in a brain surface plot in participant #3. (b) Insula electrodes projected on to a flat brain which was subsequently used for visualization of oscillation clusters and traveling waves. (c) Theta frequency oscillation cluster in participant #3 (electrodes with black circles denote electrodes without any narrowband peaks in the power spectrum). (d) Beta frequency oscillation cluster in the same participant. (e) Mean power spectrum (blue) in log–log coordinates from an example electrode in participant #3. Black line denotes fitted 1/f line to the mean power spectrum in log–log coordinates using robust linear regression (see Materials and methods). (f) Normalized power spectrum (red) after removal of the 1/f background signal. This approach emphasizes narrowband oscillations as positive deflections. Stars (cyan) denote the narrowband peaks in the normalized power spectrum, identified as any local maximum greater than one standard deviation above the mean (see Materials and methods).

Figure 4—figure supplement 1

Download asset Open asset

Figure 4—figure supplement 2

Download asset Open asset

Figure 4—figure supplement 3

Download asset Open asset

Figure 4—figure supplement 4

Download asset Open asset

Figure 4—figure supplement 5

Download asset Open asset

Figure 4—figure supplement 6

Download asset Open asset

Figure 4—figure supplement 7

Download asset Open asset

Figure 4—figure supplement 8

Download asset Open asset

Figure 4—figure supplement 9

Download asset Open asset

Oscillation clusters in participant #10.

Figure 5

Download asset Open asset

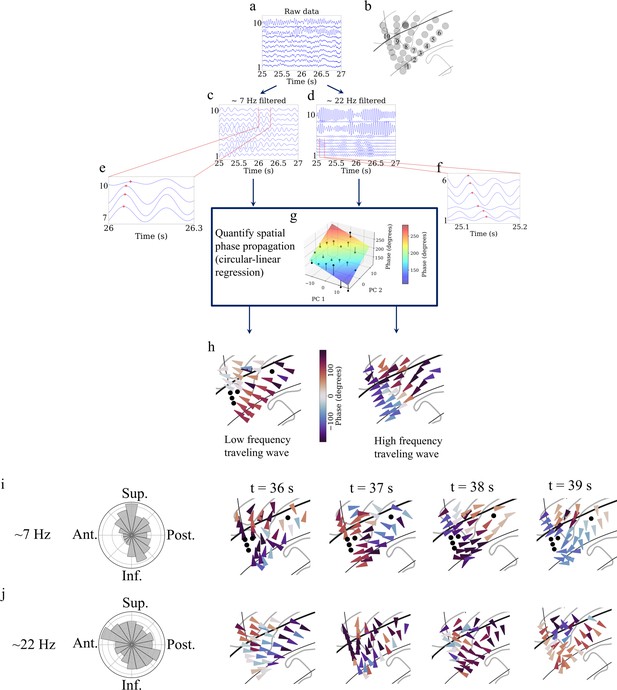
Detection of traveling waves in the human insula.

We estimated Hilbert-transformed instantaneous phases of electrodes in the oscillation clusters, and if they vary systematically with the location of the electrodes then they constitute a traveling wave. We used a localized circular-linear regression approach to detect complex patterns of traveling waves in addition to linear traveling waves, in an oscillation cluster. This localized circular-linear regression approach estimated the direction of traveling waves for each electrode (Materials and methods). (a) Raw traces from electrodes as numbered in (b) for participant #3. (c) Filtered signals in the theta frequency band. (d) Filtered signals in the beta frequency band. (e) and (f) are zoomed-in versions of filtered signals in (c) and (d), respectively, to show (denoted as red plus signs) a spatially progressive variation of the phases across the electrodes (electrodes 7–10 for theta frequency and electrodes 1–6 for beta frequency). (g) Visual demonstration of circular-linear regression approach to detect traveling waves. 3D Talairach coordinates of electrodes were mapped to 2D coordinates using principal component analysis (PCA) (PC 1 and PC 2 denote the first and second principal components, respectively) and phases of the electrodes were fitted with these coordinates in the regression model. Solid circles denote the actual phases of the electrodes with the bars denoting the residuals between the actual phases and the predicted phases (Materials and methods). (h) Left panel: arrow plot showing instantaneous propagation direction of the theta traveling wave corresponding to t=25.225 s, right panel: arrow plot showing instantaneous propagation direction of the beta traveling wave corresponding to the same time-instant as in the left panel. (i) Panel 1 shows histogram of the instantaneous propagation directions across time for theta traveling wave. Panels 2–5: arrow plots showing variation of instantaneous propagation directions of the theta traveling waves corresponding to t=36 s, 37 s, 38 s, and 39 s, respectively. (j) Panel 1 shows histogram of the instantaneous propagation directions across time for the beta traveling wave. Panels 2–5: arrow plots showing variation of instantaneous propagation directions of beta traveling waves corresponding to t=36 s, 37 s, 38 s, and 39 s, respectively. Ant: anterior; Post: posterior; Sup: superior; Inf: inferior.

Figure 6

Download asset Open asset

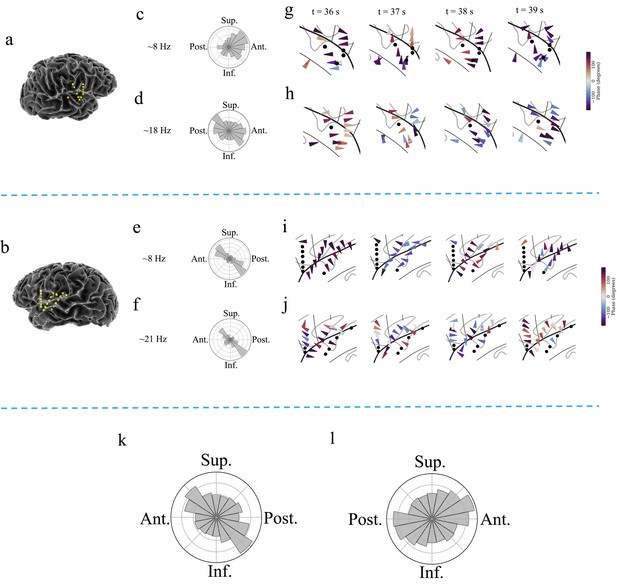
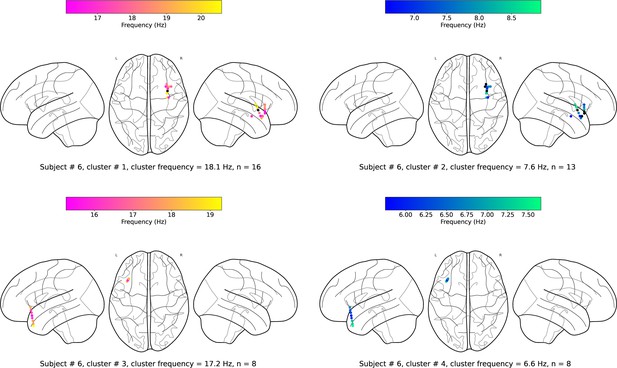
Examples of traveling waves in the human insula.

Traveling waves changed their directions with respect to time. Insula electrodes visualized in a brain surface plot in (a) participant #6 and (b) participant #7. (c) and (d) are histograms of the instantaneous propagation directions across time for theta (~8 Hz) and beta (~18 Hz) traveling waves in participant #6. (e) and (f) are the same as in (c) and (d), respectively, for participant #7. (g) Panels 1–4: arrow plots showing variation of instantaneous propagation direction of theta traveling waves corresponding to t=36 s, 37 s, 38 s, and 39 s, respectively, in participant #6, visualized in a zoomed-in version of flat brain. (h) Panels 1–4: arrow plots showing instantaneous propagation directions of beta traveling waves corresponding to t=36 s, 37 s, 38 s, and 39 s, respectively, in participant #6, visualized in a zoomed-in version of flat brain. (i) and (j) are same as in (g) and (h), respectively, for participant #7. (k) and (l) are the histograms of the instantaneous propagation directions of traveling waves across time, clusters, and participants for left and right insula, respectively. Solid circles represent electrodes without narrowband oscillations. Ant: anterior; Post: posterior; Sup: superior, Inf: inferior.

Figure 7

Download asset Open asset

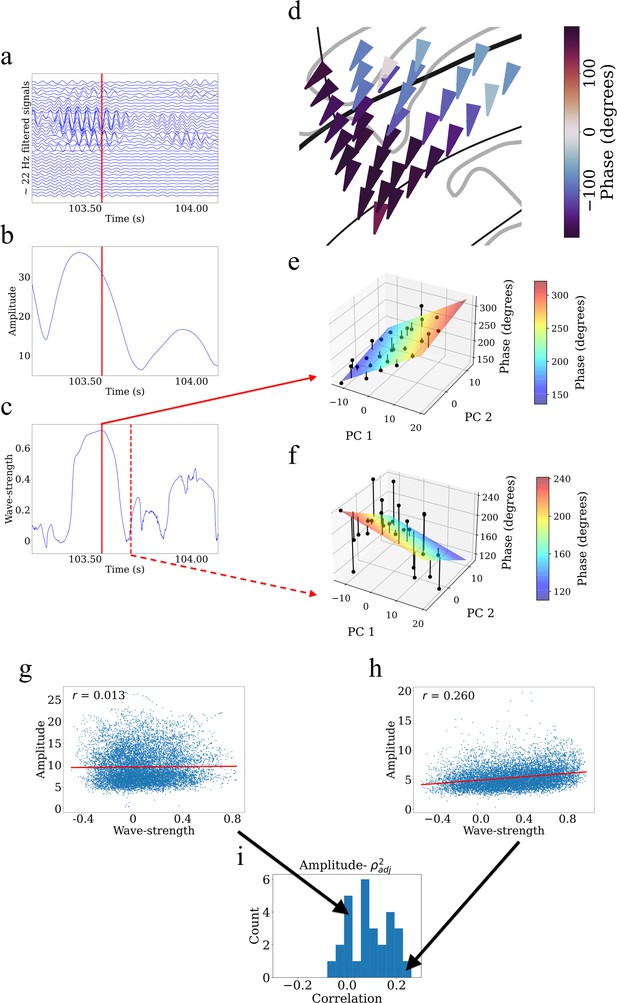
Example showing that higher wave-strength values of traveling waves correspond to higher Hilbert-transformed amplitude of signals in participant #3.

(a) Filtered signals in the beta frequency band from all electrodes in participant #3 in time interval 103.25 s to 104.125 s. (b) Average amplitude across all electrodes in the same time interval. We defined the average amplitude for each oscillation cluster to be the average of the Hilbert-transformed instantaneous amplitudes of filtered signals of all electrodes. (c) Wave-strength, averaged across all electrodes, in the same time interval. Higher wave-strength corresponds to higher amplitudes of electrodes in (b) (But observe that the amplitude peaks earlier than the wave-strength; see Results). Time-instant corresponding to the local maximum of wave-strength in (c) is denoted by the red lines in (a), (b), and (c). (d) Arrow plot showing instantaneous propagation direction of electrodes for the beta traveling wave at the time-instant corresponding to the red line in (c). Note the smooth variation of phases across space, which results in the high value of wave-strength in (c). (e) Circular-linear regression fit at the time-instant corresponding to the red line in (c). Solid circles denote the actual phases of the electrodes with the bars denoting the residuals between the actual phases and the predicted phases. Note the relatively low values of the residuals indicated by the low heights of the bars. (f) Circular-linear regression fit at a time-instant (denoted as dotted red line in (c)) for which the wave-strength is relatively low. Note the relatively high values of the residuals. (**g–i**) Strength (denoted as $ρ_{a d j}^{2}$ ) of traveling waves is positively correlated with Hilbert-transformed amplitude of signals. We estimated the average (averaged across electrodes) Hilbert-transformed instantaneous amplitudes of signals of the electrodes for each oscillation cluster and estimated their correlation with the wave-strength of traveling waves. We used a circular-shuffling procedure to test the significance of correlations where we circularly shuffle the wave-strength values with respect to the average amplitude and estimate the correlation on this shuffled data to build a distribution of surrogate correlation values against which the observed correlation was tested (p<0.05) (Materials and methods). (g) Amplitude- $ρ_{a d j}^{2}$ scatter plot for cluster 1 of participant #7 where there was no statistically significant correlation (p>0.05). (h) Amplitude- $ρ_{a d j}^{2}$ scatter plot for cluster 2 of participant #8 where there was a statistically significant correlation (p<0.05). (i) Histogram of correlations across all clusters (also see Supplementary file 1a).

Additional files

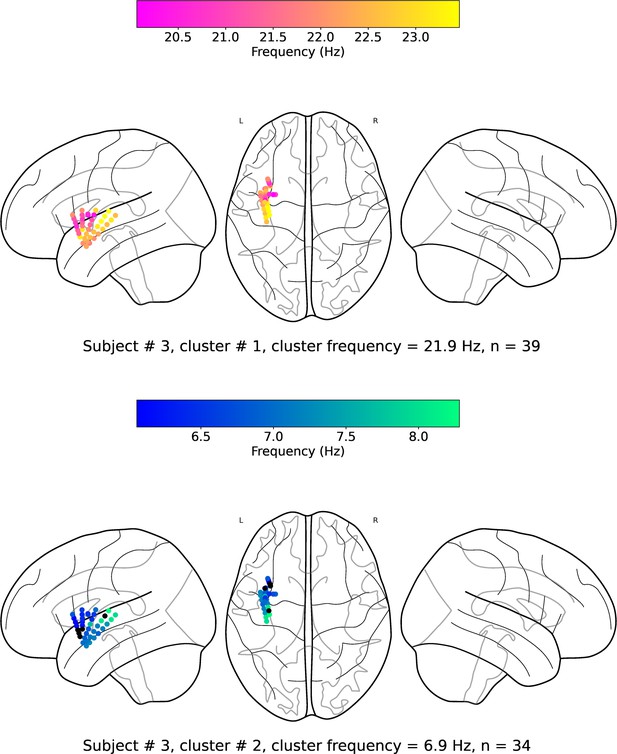
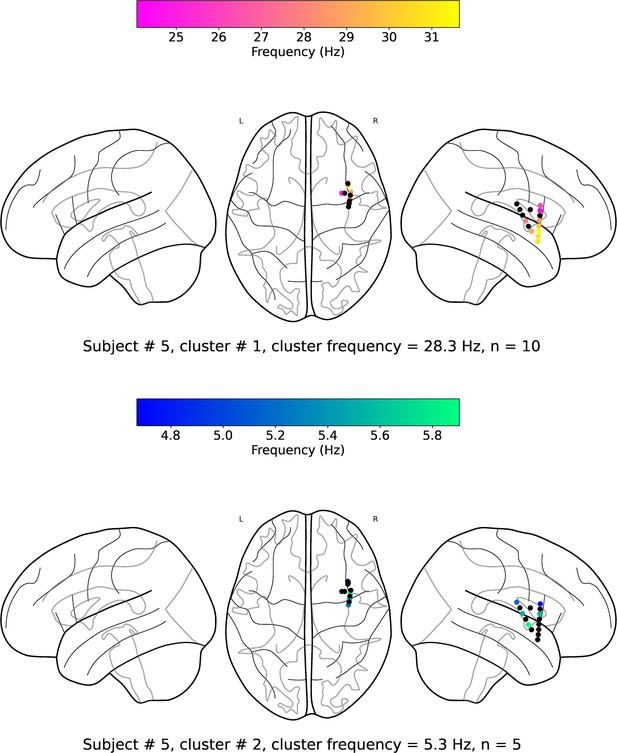
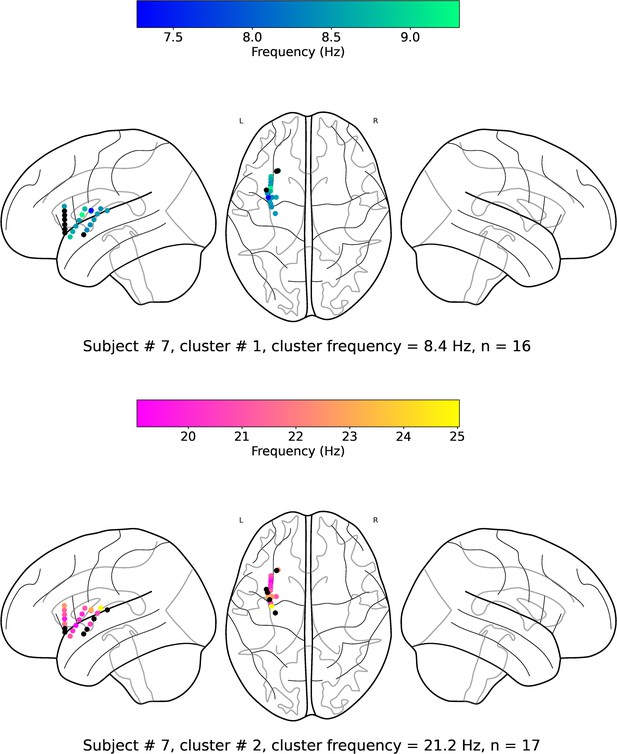
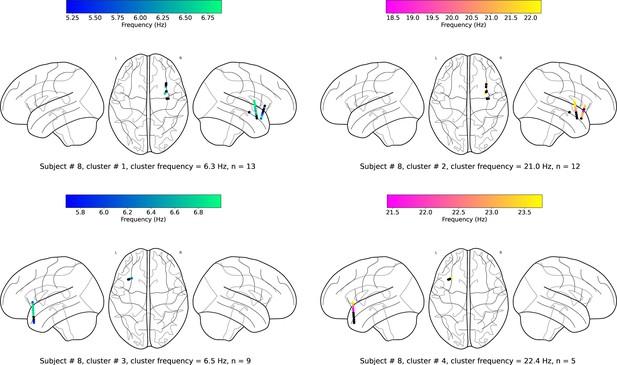
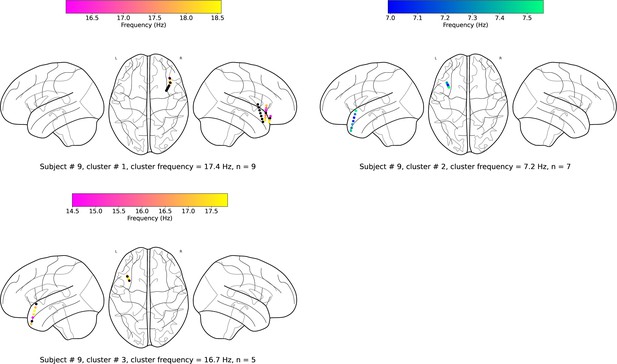
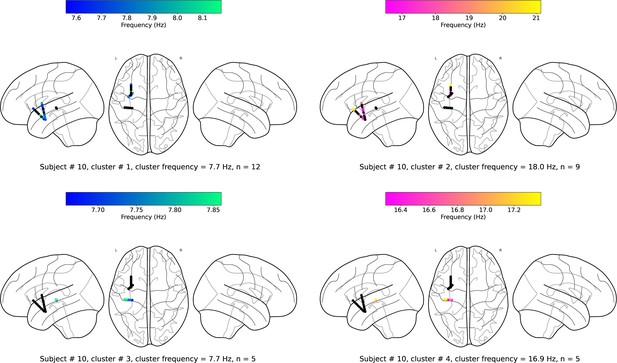
Supplementary file 1 Supplementary File for “Spontaneous Neuronal Oscillations in the Human Insula are Hierarchically Organized Traveling Waves”. (a). Wave-strength (denoted as $ρ_{a d j}^{2}$ ) of traveling waves is positively correlated with Hilbert-transformed amplitude of signals. We estimated the correlation between the average amplitude of signals of the electrodes and the wave-strength of traveling waves for each oscillation cluster. We used a circular-shuffling procedure to test the significance of correlations where we circularly shuffle the wave-strength values with respect to the average amplitude and estimate the correlation on this shuffled data to build a distribution of surrogate correlation values against which the observed correlation was tested (p<0.05) (Materials and methods). We found that for ~71% of clusters (20 out of the 28 clusters), there was a statistically significant correlation between amplitude and wave-strength. All, except one, clusters out of these 20 clusters, showed a statistically significant positive amplitude- $ρ_{a d j}^{2}$ correlation. Cluster frequency for an oscillation cluster was defined to be the average of the oscillation frequencies across all electrodes for the given oscillation cluster. (b). Wave-strength (denoted as $ρ_{a d j}^{2}$ ) of high (beta) frequency traveling waves is uncorrelated with the wave-strength ( $ρ_{a d j}^{2}$ (low)- $ρ_{a d j}^{2}$ (high)), phase (phase (low)- $ρ_{a d j}^{2}$ (high)), and power (power (low)- $ρ_{a d j}^{2}$ (high)) of low (theta) frequency traveling waves. For testing the statistical significance of the observed correlations, values from one time-series were circularly shuffled with respect to the other so that the instantaneous correlation between the two time-series is destroyed, and correlation analysis was repeated on this shuffled data to build a distribution of surrogate correlation values against which the observed correlation was tested (p<0.05) (Materials and methods).: https://cdn.elifesciences.org/articles/76702/elife-76702-supp1-v2.docx
Download elife-76702-supp1-v2.docx
Transparent reporting form: https://cdn.elifesciences.org/articles/76702/elife-76702-transrepform1-v2.docx
Download elife-76702-transrepform1-v2.docx