Time-resolved parameterization of aperiodic and periodic brain activity
- McConnell Brain Imaging Centre, Montreal Neurological Institute, McGill University, Canada
Figures
Figure 1 with 1 supplement
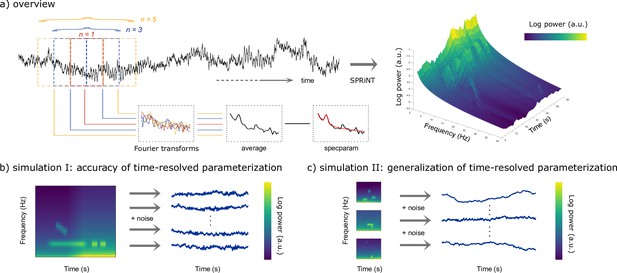
Methods synopsis.
(a) Overview of the Spectral Parameterization Resolved in Time (SPRiNT) approach: At each time bin along a neurophysiological time series (black trace) n overlapping time windows are Fourier-transformed to yield an estimate of spectral contents, which is subsequently parameterized using specparam (Donoghue et al., 2020). The procedure is replicated across time over sliding, overlapping windows to generate a parameterized spectrogram of neural activity. (b) Simulation challenge I: We simulated 10,000 time series composed of the same time-varying spectral (aperiodic and periodic) features, with different realizations of additive noise. (c) Simulation challenge II: We simulated another 10,000 time series, each composed of different time-varying spectral (aperiodic and periodic) ground-truth features with additive noise. All simulated time series were used to evaluate the respective performances of SPRiNT and the wavelet-specparam alternative.
Figure 1—figure supplement 1
Overview of the outlier peak removal process.
(a) Original Spectral Parameterization Resolved in Time (SPRiNT) spectrogram (top) and time-frequency distribution of peak centre frequencies (bottom). In this example, the detected peaks (red and blue dots) are sequentially removed if they are not part of a cluster of contiguous peaks within a time-frequency region of 3 s by 2.5 Hz (red dots; size of minimum cluster is adjustable by user). (b) Resulting SPRiNT spectrogram (top) and peak centre frequencies (bottom) after outlier removal and the update of aperiodic parameters. Dashed rectangular areas show time-frequency regions where periodic activity was simulated in the synthesized signal.
Figure 2 with 4 supplements
Spectral Parameterization Resolved in Time (SPRiNT) vs wavelet-specparam performances (simulation challenge I).
(a) Ground-truth spectrogram (left) and averaged modelled spectrograms produced by the wavelet-specparam approach (middle) and SPRiNT (right; n=10,000). (b) Aperiodic parameter estimates (lines: median; shaded regions: first and third quartiles, n=10,000) across time from wavelet-specparam (left) and SPRiNT (right; black: ground truth; blue: exponent; yellow: offset). (c) Absolute error (and detection performance) of alpha and beta-band rhythmic components for wavelet-specparam (left) and SPRiNT (right). Violin plots represent the sample distributions (n=10,000; blue: alpha peak; yellow: beta peak; white circle: median, grey box: first and third quartiles; whiskers: range).
Figure 2—figure supplement 1
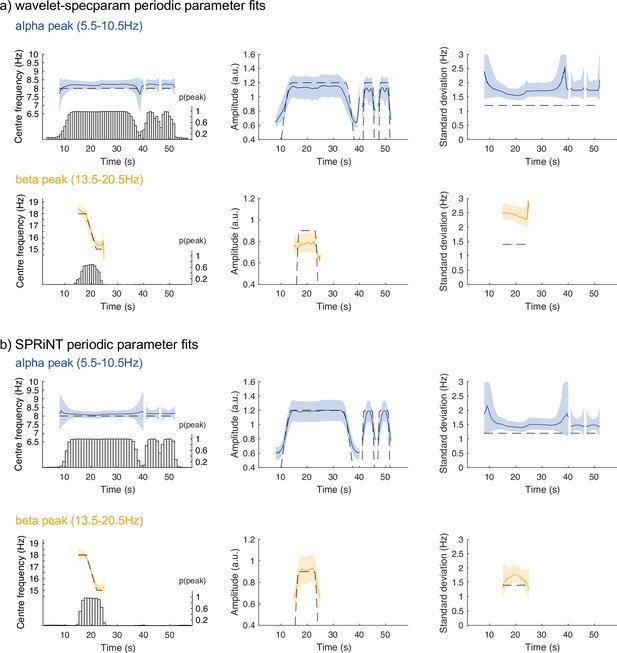
Periodic parameter estimates across time.
(a) Results from the temporally smoothed wavelet-specparam approach for the alpha (top) and beta (bottom) rhythmic components for each estimated parameter (from left to right: centre frequency, spectral peak amplitude, and SD). Grey dashed line: ground truth; coloured line: median; shaded region: first and third quartiles. Bar plots in left panels: probability of detecting an oscillatory peak within respective frequency ranges at each time bin. (b) Same display for the results obtained with Spectral Parameterization Resolved in Time (SPRiNT). All with n=10,000 simulations.
Figure 2—figure supplement 2
Wavelet-specparam performances at varying spectral/temporal resolutions.
(a) Aperiodic parameter estimates (lines: median; shaded regions: first and third quartiles, n=1000) across time from wavelet-specparam with full width at half maximum (FWHM) = 2 s (left) and wavelet-specparam with FWHM = 4 s (right; black dash: ground truth; blue: exponent; yellow: offset). (b) Absolute error (and detection performance) of alpha and beta-band rhythmic components for wavelet-specparam with FWHM = 2 s (left) and wavelet-specparam with FWHM = 4 s (right). Violin plots represent the sample distributions (n=1000; blue: alpha peak; yellow: beta peak; white circle: median, grey box: first and third quartiles; whiskers: range).
Figure 2—figure supplement 3
Spectral Parameterization Resolved in Time (SPRiNT) performances at varying spectral/temporal resolutions.
(a) Aperiodic parameter estimates (lines: median; shaded regions: first and third quartiles, n=1000) across time from SPRiNT spectrograms obtained from 5×1 s time windows with 75% overlap (left) vs 5×2 s windows with 75% overlap (right; black dash: ground truth; blue: exponent; yellow: offset). (b) Absolute error (and detection performance) of alpha and beta-band periodic components for SPRiNT using 5×1 s time windows with 75% overlap (left) and 5×2 s time windows with 75% overlap (right). Violin plots represent the sample distributions (n=1000; blue: alpha peak; yellow: beta peak; white circle: median, grey box: first and third quartiles; whiskers: range).
Figure 2—figure supplement 4
Raw performances of Spectral Parameterization Resolved in Time (SPRiNT) and wavelet-specparam (without temporal smoothing and outlier peak removal).
(a) Aperiodic parameter estimates (lines: median; shaded regions: first and third quartiles, n=1000) across time from unsmoothed wavelet-specparam (left) and SPRiNT without outlier peak removal (right; black dash: ground truth; blue: exponent; yellow: offset). (b) Absolute error (and detection performance) of alpha and beta-band periodic components for unsmoothed wavelet-specparam (left) and SPRiNT without outlier peak removal (right). Violin plots represent the sample distributions (n=1000; blue: alpha peak; yellow: beta peak; white circle: median, grey box: first and third quartiles; whiskers: range).
Figure 3 with 3 supplements
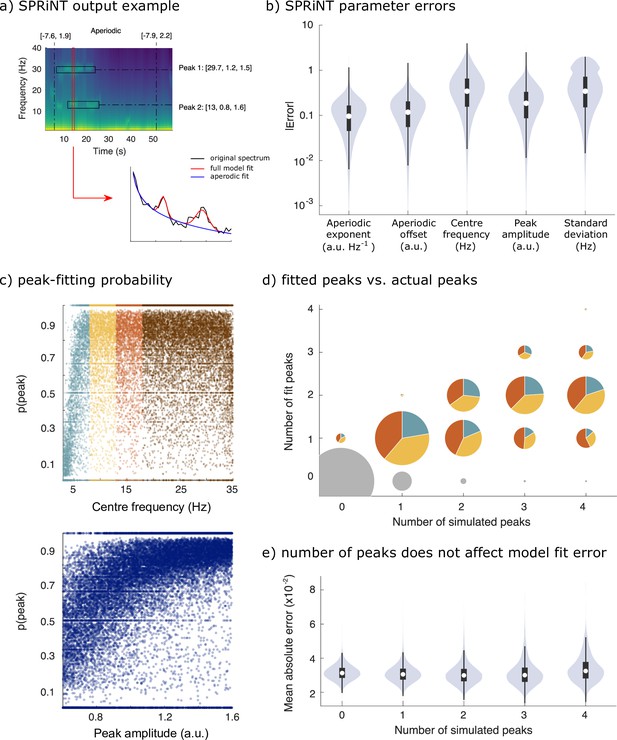
Spectral Parameterization Resolved in Time (SPRiNT) performances (simulation challenge II).
(a) SPRiNT parameterized spectrogram for a representative simulated time series with time-varying aperiodic (offset and exponent) and transient periodic (centre frequency, amplitude, and SD) components. The red arrow indicates a cross-sectional view of the spectrogram at 14 s. (b) Absolute error in SPRiNT parameter estimates across all simulations (n=10,000). (c) Detection probability of spectral peaks (i.e., rhythmic components) depending on simulated centre frequency and amplitude (light blue: 3–8 Hz theta; yellow: 8–13 Hz alpha; orange: 13–18 Hz beta; brown:18–35 Hz). (d) Number of fitted vs simulated periodic components (spectral peaks) across all simulations and time points. The underestimation of the number of estimated spectral peaks is related to centre frequency: 3–8 Hz simulated peaks (light blue) account for proportionally fewer of recovered peaks between 3 and 18 Hz (light blue, yellow, and orange) than from the other two frequency ranges. Samples sizes by number of simulated peaks: 0 peaks = 798,753, 1 peak = 256,599, 2 peaks = 78,698, 3 peaks = 14,790, 4 peaks = 1160. (e) Model fit error is not affected by number of simulated peaks. Violin plots represent the full sample distributions (white circle: median, grey box: first and third quartiles; whiskers: range).
-
Figure 3—source data 1
Figure data for simulation challenge II.
- https://cdn.elifesciences.org/articles/77348/elife-77348-fig3-data1-v1.zip
Figure 3—figure supplement 1
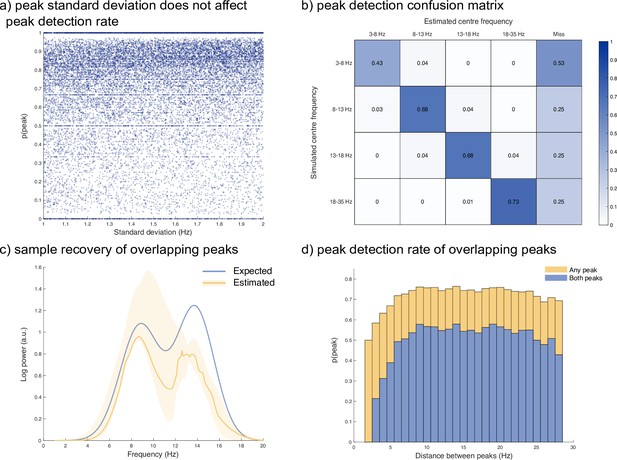
Performances of Spectral Parameterization Resolved in Time (SPRiNT) across a range of peak SD, frequency band, and spectral separation between peaks.
(a) Detection probability of spectral peaks (i.e., rhythmic components) did not depend on simulated SD (bandwidth). (b) Confusion matrix of estimated centre frequency range against simulated centre frequency range. 3–8 Hz peaks were more challenging to detect than other frequency ranges. (c) Sample estimated shape (yellow: median; shaded areas: first and third quartiles) of two simulated spectral peaks (blue; peak 1 [centre frequency, amplitude, and SD]: 8.8 Hz, 1.1 a.u, and 1.8 Hz; peak 2: 13.8 Hz, 1.2 a.u., and 1.7 Hz) overlapping in frequency space. (d) Individual (any peak; yellow) and joint (both peaks; blue) peak detection rate as a function of the proximity of two peaks simultaneously present. Individual and joint peak detection probability was lower when two peaks were within 8 Hz of one another.
Figure 3—figure supplement 2
Performances of Spectral Parameterization Resolved in Time (SPRiNT) on broad-range spectrograms comprising spectral knees.
(a) SPRiNT parameterized spectrogram for a representative simulated time series with time-varying aperiodic (offset and exponent) and two periodic (centre frequency, amplitude, and SD) components, with a static knee component. One peak is in a lower frequency range (3–30 Hz), while the other is in a higher frequency range (30–80 Hz). The red arrow indicates a cross-sectional view of the spectrogram at 20 s (in log-frequency space). (b) Absolute error in SPRiNT aperiodic parameter estimates across all simulations (n=1000) (c) Absolute error in SPRiNT periodic parameter estimates across all simulations (blue: 3–30 Hz; yellow: 30–80 Hz; n=1000). Violin plots represent the full-sample distributions (white circle: median; grey box: first and third quartiles; whiskers: range).
Figure 3—figure supplement 3
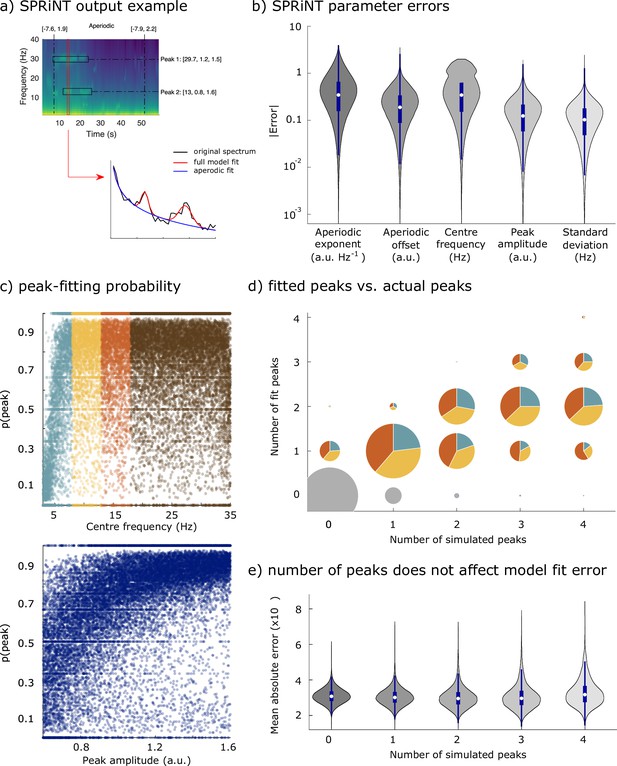
Performances of Spectral Parameterization Resolved in Time (SPRiNT) (without outlier peak removal).
(a) SPRiNT parameterized spectrogram for a representative simulated time series with time-varying aperiodic (offset and exponent) and transient periodic (centre frequency, amplitude, and SD) components. The red arrow indicates a cross-sectional view of the spectrogram at 14 s. (b) Absolute error in SPRiNT parameter estimates across all simulations (n=10,000). (c) Detection probability of spectral peaks (i.e., rhythmic components) depending on simulated centre frequency and amplitude (light blue: 3–8 Hz theta; yellow: 8–13 Hz alpha; orange: 13–18 Hz beta). (d) Number of fitted vs simulated periodic components across all simulations and time points. The underestimation of the number of estimated spectral peaks is related to centre frequency: 3–8 Hz simulated peaks (blue) account for proportionally fewer of recovered peaks between 3 and 18 Hz (blue, yellow, and orange) than from the other two frequency ranges (samples sizes by number of simulated peaks: 0 peaks = 798,753, 1 peak = 256,599, 2 peaks = 78,698, 3 peaks = 14,790, and 4 peaks = 1160). (e) Model fit error is not affected by number of simulated peaks. Violin plots show the full sample distributions (white circle: median, blue box: first and third quartiles; whiskers: range).
Figure 4 with 1 supplement
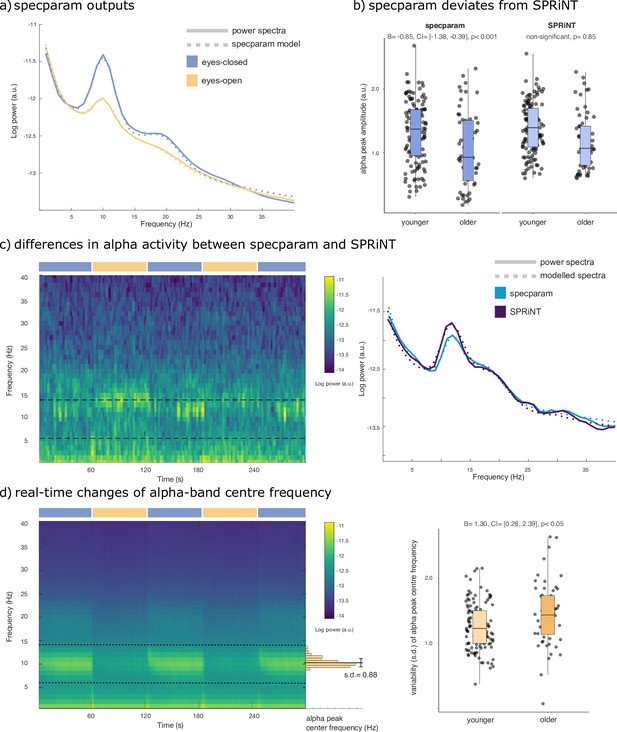
Spectral Parameterization Resolved in Time (SPRiNT) parameterization of resting-state EEG.
(a) Mean periodogram and specparam models for eyes-closed (blue) and eyes-open (yellow) resting-state EEG activity (from electrode Oz; n=178). (b) Logistic regressions showed that specparam-derived eyes-closed alpha-peak amplitude was predictive of age group, but mean eyes-closed alpha-peak amplitude derived from SPRiNT was not. (c) Example of intrinsic dynamics in alpha activity during the eyes-closed period leading to divergent SPRiNT and specparam models (participant sub-016). In a subset of participants (<10%), we observed strong intermittence of the presence of an alpha peak. Since an alpha peak was not consistently present in the eyes-closed condition, and specparam-derived alpha-peak amplitude (0.77 a.u.; light blue) is lower than SPRiNT-derived mean alpha-peak amplitude (1.06 a.u.; dark blue), as the latter only includes time samples featuring a detected alpha peak. (d) Logistic regression showed that temporal variability in eyes-open alpha centre frequency predicts age group. Left: mean SPRiNT spectrogram (n=178) and sample distribution of eyes-open alpha centre frequency (participant sub-067). Right: variability (SD) in eyes-open alpha centre frequency separated by age group. Note: no alpha peaks were detected in the eyes-open period for one participant (boxplot line: median; boxplot limits: first and third quartiles; whiskers: range). Sample sizes: younger adults (age: 20–40 years): 121; older adults (age: 55–80 years): 56.
-
Figure 4—source data 1
Spectral parameters and age group by participant.
- https://cdn.elifesciences.org/articles/77348/elife-77348-fig4-data1-v1.zip
Figure 4—figure supplement 1
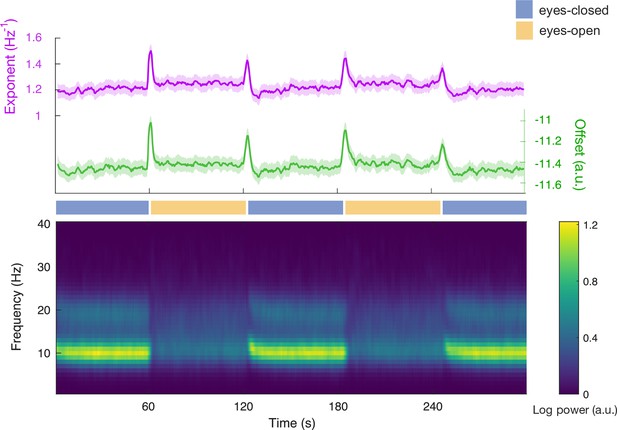
Spectral Parameterization Resolved in Time (SPRiNT) model parameters in resting-state EEG.
SPRiNT aperiodic parameters (top panel; line: group mean [n=178]; shaded region: 95% CI) and SPRiNT periodic activity averaged across participants (bottom panel).
Figure 5 with 3 supplements
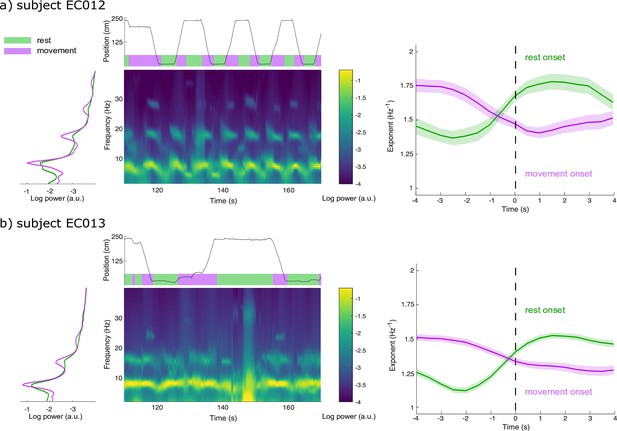
Spectral Parameterization Resolved in Time (SPRiNT) captures aperiodic dynamics related to locomotion.
(a) We derived the data periodograms collapsed across rest (green) and movement (purple) periods for subject EC012 and observed broad increases in signal power during rest compared to movement, below 20 Hz. A representative SPRiNT spectrogram is shown. The time series of the subject’s position is shown in the top plot (green: rest; purple: movement). We observed gradual shifts of aperiodic exponent around the occurrence of locomotor transitions (right plot), with increasing exponents at the onset of rest (green curve) and decreasing exponents at movement onset (purple curve). Solid lines indicated trial mean, with shaded area showing the 95% CI. (b) Same data as (a) but for subject EC013. The data samples consisted of, for EC012, 62 epochs of rest onset and 81 epochs of movement onset; for EC013, 303 epochs of rest onset and 254 epochs of movement onset.
-
Figure 5—source data 1
Empirical distributions of Spectral Parameterization Resolved in Time (SPRiNT) aperiodic parameters.
- https://cdn.elifesciences.org/articles/77348/elife-77348-fig5-data1-v1.zip
Figure 5—figure supplement 1
Examples of sawtooth rhythms from two representative electrodes in entorhinal cortex layer 3 from both subjects.
(a) Example time-series of prominent sawtooth rhythms from two representative electrodes during a movement bout for subject EC012 (top), producing harmonics of activity in the average modelled spectrogram (bottom). (b) Same as (a) for subject EC013.
Figure 5—figure supplement 2
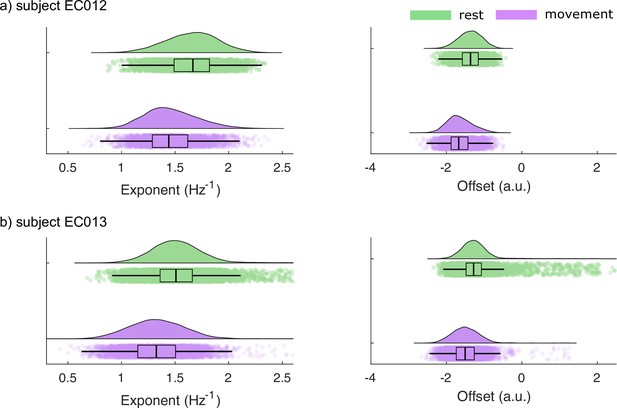
Empirical distributions of Spectral Parameterization Resolved in Time (SPRiNT) aperiodic exponent and offset parameters.
(a) Empirical distributions of aperiodic exponent and offset estimates for subject EC012 at time bins associated with rest (green) and movement (purple) bouts (boxplot line: median; boxplot limits: first and third quartiles; whiskers: range). (b) Same as (a) for subject EC013. Sample sizes: EC012 rest (movement)=3584 (4325) bins; EC013 rest (movement)=9238 (6672) bins.
Figure 5—figure supplement 3
Temporal variability of aperiodic exponent during transitions between movement and rest is partially explained by movement speed.
(a) Empirical distributions and linear regression of aperiodic exponent against movement speeds for subject EC012 during transitions to rest. (b) Same as (a) for transitions to movement. (c) Same as (a) for subject EC013. (d) Same as (b) for subject EC013. Line: linear model fit; shaded area: model 95% CI. Sample sizes: EC012 transition to rest (movement)=1054 (1377); EC013 rest (movement)=5151 (4,318).
Author response image 1
Example periodic components with differing spectral signal-to-noise ratios.
(a) Example parameterized periodogram (exponent: 1 a.u. Hz-1; offset: -6 a.u.; α peak centre frequency, amplitude, standard deviation: 10 Hz, 1.0 a.u., 1 Hz, respectively) with a derived log-SNR of 5. (b) Example parameterized periodogram (exponent: 1 a.u. Hz-1; offset: -6 a.u.; α peak centre frequency, amplitude, standard deviation: 10 Hz, 1.0 a.u., 1 Hz, respectively) with a derived log-SNR of 5. The log-SNR of each periodic component is calculated as the ratio of peak amplitude divided by one standard deviation of the intrinsic spectral noise (0.2 a.u.).
Tables
Table 1
Logistic regression model of specparam parameters for predicting condition (eyes-closed vs eyes-open).
| Predictors | Condition | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | 0.86 | –1.85–3.64 | 0.537 | |
| Alpha centre frequency (specparam) | 0.00 | –0.23–0.23 | 0.990 | 7.97 |
| Alpha amplitude (specparam) | –2.73 | –3.42 to –2.11 | <0.001 | 3.21 e-21 |
| Aperiodic exponent (specparam) | 1.14 | 0.33–1.99 | 0.007 | 0.20 |
| Observations | 323 | |||
| R2 Tjur | 0.284 | |||
Table 2
Logistic regression model of Spectral Parameterization Resolved in Time (SPRiNT) parameters for predicting condition (eyes-closed vs eyes-open).
| Condition | ||||
|---|---|---|---|---|
| Predictors | Log-Odds | CI | p | BF |
| (Intercept) | 0.10 | –3.75–4.02 | 0.959 | |
| Mean alpha centre frequency | 0.24 | –0.04–0.52 | 0.101 | 1.58 |
| Std alpha centre frequency | –0.06 | –0.97–0.86 | 0.898 | 4.39 |
| Mean alpha power | –6.31 | –8.23 to –4.61 | <0.001 | 4.51e-13 |
| Std alpha power | 4.64 | 0.76–8.73 | 0.022 | 3.81 |
| Mean aperiodic slope | 2.55 | 1.55–3.63 | <0.001 | 1.62e-4 |
| Std aperiodic slope | –2.74 | –8.54–3.38 | 0.362 | 4.32 |
| Observations | 355 | |||
| R2 Tjur | 0.432 | |||
Table 3
Logistic regression model of Spectral Parameterization Resolved in Time (SPRiNT) parameters for predicting condition (eyes-closed vs eyes-open), with model fit error (mean absolute error [MAE]) as a predictor.
| Predictors | Condition | ||
|---|---|---|---|
| Log-Odds | CI | p | |
| (Intercept) | –1.37 | –8.83–4.07 | 0.620 |
| Mean alpha centre frequency | 0.23 | –0.05–0.51 | 0.115 |
| Std alpha centre frequency | –0.15 | –1.08–0.79 | 0.751 |
| Mean alpha power | –6.62 | –8.73 to –4.73 | <0.001 |
| Std alpha power | 5.15 | 1.05–9.46 | 0.016 |
| Mean aperiodic slope | 2.63 | 1.60–3.73 | <0.001 |
| Std aperiodic slope | –3.79 | –10.21–2.89 | 0.253 |
| Model fit MAE | 59.96 | –95.00–215.29 | 0.447 |
| Observations | 355 | ||
| R2 Tjur | 0.433 | ||
Table 4
Logistic regression model parameters for predicting condition (eyes-closed vs eyes-open) from Morlet wavelet spectrograms.
| Condition | ||||
|---|---|---|---|---|
| Predictors | Log-Odds | CI | p | BF |
| (Intercept) | –25.98 | –33.87 to –18.65 | <0.001 | |
| Alpha power (Morlet wavelets) | –2.05 | –2.67 to –1.47 | <0.001 | 1.08e-11 |
| Observations | 356 | |||
| R2 Tjur | 0.148 | |||
Table 5
Eyes-open logistic regression model parameters for predicting age group, Spectral Parameterization Resolved in Time (SPRiNT).
| Predictors | Age | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | 1.92 | –2.82–6.80 | 0.428 | |
| Eyes-open mean alpha centre frequency | –0.05 | –0.39–0.29 | 0.789 | 3.43 |
| Eyes-open std alpha centre frequency | 1.30 | 0.28–2.39 | 0.015 | 0.20 |
| Eyes-open mean alpha power | 0.41 | –2.69–3.27 | 0.784 | 2.97 |
| Eyes-open std alpha power | –3.81 | –9.47–1.54 | 0.172 | 1.14 |
| Eyes-open mean aperiodic slope | –3.31 | –4.88 to –1.91 | <0.001 | 5.14e-05 |
| Eyes-open std aperiodic slope | 3.44 | –4.83–11.06 | 0.388 | 2.66 |
| Observations | 177 | |||
| R2 Tjur | 0.216 | |||
Table 6
Eyes-closed logistic regression model parameters for predicting age group, Spectral Parameterization Resolved in Time (SPRiNT).
| Predictors | Age | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | 11.23 | 4.63–18.50 | 0.001 | |
| Eyes-closed mean centre frequency | –0.74 | –1.28 to –0.24 | 0.006 | 0.07 |
| Eyes-closed std centre frequency | 1.01 | –0.48–2.56 | 0.188 | 1.65 |
| Eyes-closed mean alpha power | –0.15 | –1.76–1.43 | 0.852 | 3.90 |
| Eyes-closed std alpha power | –0.51 | –5.32–4.22 | 0.831 | 3.61 |
| Eyes-closed mean aperiodic slope | –4.34 | –6.10 to –2.79 | <0.001 | 1.10e-07 |
| Eyes-closed std aperiodic slope | 0.54 | –9.66–9.45 | 0.910 | 3.93 |
| Observations | 178 | |||
| R2 Tjur | 0.272 | |||
Table 7
Eyes-open logistic regression model parameters for predicting age group, short-time Fourier transform (STFT).
| Predictors | Age | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | –0.44 | –3.04–2.11 | 0.734 | |
| Eyes-open mean individual alpha-peak frequency (STFT) | –0.17 | –0.45–0.11 | 0.233 | 2.33 |
| Eyes-open std individual alpha-peak frequency (STFT) | 0.63 | 0.04–1.24 | 0.040 | 0.59 |
| Observations | 178 | |||
| R2 Tjur | 0.026 | |||
Table 8
Eyes-closed logistic regression model parameters for predicting age group, short-time Fourier transform (STFT).
| Predictors | Age | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | 1.83 | –1.98–5.75 | 0.350 | |
| Eyes-closed mean individual alpha-peak frequency (STFT) | –0.31 | –0.70–0.07 | 0.113 | 1.28 |
| Eyes-closed std individual alpha-peak frequency (STFT) | 0.30 | –0.22–0.81 | 0.256 | 2.32 |
| Observations | 178 | |||
| R2 Tjur | 0.024 | |||
Table 9
Eyes-open logistic regression model parameters for predicting age group, specparam.
| Age | ||||
|---|---|---|---|---|
| Predictors | Log-Odds | CI | p | BF |
| (Intercept) | 7.61 | 3.63–12.09 | <0.001 | |
| Eyes-open aperiodic exponent (specparam) | –3.30 | –5.08 to –1.74 | <0.001 | 4.61 e-4 |
| Eyes-open alpha centre frequency (specparam) | –0.35 | –0.68 to –0.05 | 0.028 | 0.26 |
| Eyes-open alpha amplitude (specparam) | –1.34 | –2.86–0.02 | 0.066 | 0.72 |
| Observations | 147 | |||
| R2 Tjur | 0.207 | |||
Table 10
Eyes-closed logistic regression model parameters for predicting age group, specparam.
| Predictors | Age | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | 12.40 | 7.11–18.50 | <0.001 | |
| Eyes-closed aperiodic exponent (specparam) | –2.67 | –3.94 to –1.54 | <0.001 | 3.22e-5 |
| Eyes-closed alpha centre frequency (specparam) | –0.85 | –1.38 to –0.39 | 0.001 | 3.61e-3 |
| Eyes-closed alpha amplitude (specparam) | –0.96 | –1.72 to –0.24 | 0.010 | 0.11 |
| Observations | 176 | |||
| R2 Tjur | 0.246 | |||
Table 11
Eyes-closed logistic regression model parameters for predicting age group, Morlet wavelets.
| Predictors | Age | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | –14.93 | –24.68 to –5.89 | 0.002 | |
| Eyes-closed alpha power (Morlet wavelets) | –1.13 | –1.90 to –0.41 | 0.003 | 0.07 |
| Observations | 178 | |||
| R2 Tjur | 0.053 | |||
Table 12
Eyes-open logistic regression model parameters for predicting age group, Morlet wavelets.
| Predictors | Age | |||
|---|---|---|---|---|
| Log-Odds | CI | p | BF | |
| (Intercept) | –9.04 | –21.73–3.13 | 0.152 | |
| Eyes-open alpha power (Morlet wavelets) | –0.64 | –1.63–0.30 | 0.189 | 2.74 |
| Observations | 178 | |||
| R2 Tjur | 0.010 | |||
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Time-resolved parameterization of aperiodic and periodic brain activity
eLife 11:e77348.
https://doi.org/10.7554/eLife.77348
