Figures and data in Limitations of principal components in quantitative genetic association models for human studies

Figures
Tables
Additional files

8 figures, 7 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

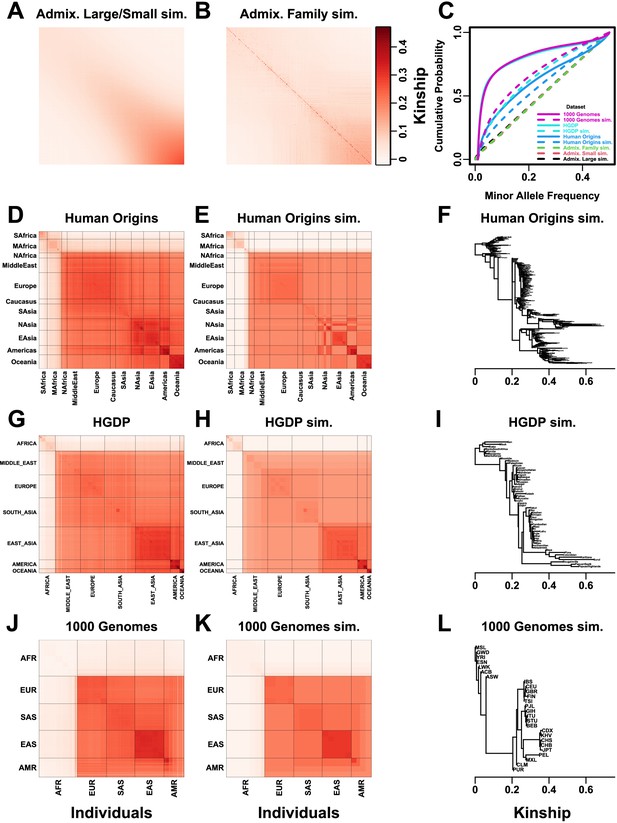
Population structures of simulated and real human genotype datasets.

First two columns are population kinship matrices as heatmaps: individuals along x- and y-axis, kinship as color. Diagonal shows inbreeding values. (A) Admixture scenario for both Large and Small simulations. (B) Last generation of 20-generation admixed family, shows larger kinship values near diagonal corresponding to siblings, first cousins, etc. (C) Minor allele frequency (MAF) distributions. Real datasets and subpopulation tree simulations had $MAF \geq 0.01$ filter. (D) Human Origins is an array dataset of a large diversity of global populations. (G) Human Genome Diversity Panel (HGDP) is a WGS dataset from global native populations. (J) 1000 Genomes Project is a WGS dataset of global cosmopolitan populations. (**F, I, L**) Trees between subpopulations fit to real data. (**E, H, K**). Simulations from trees fit to the real data recapitulate subpopulation structure.

Figure 2 with 3 supplements

Download asset Open asset

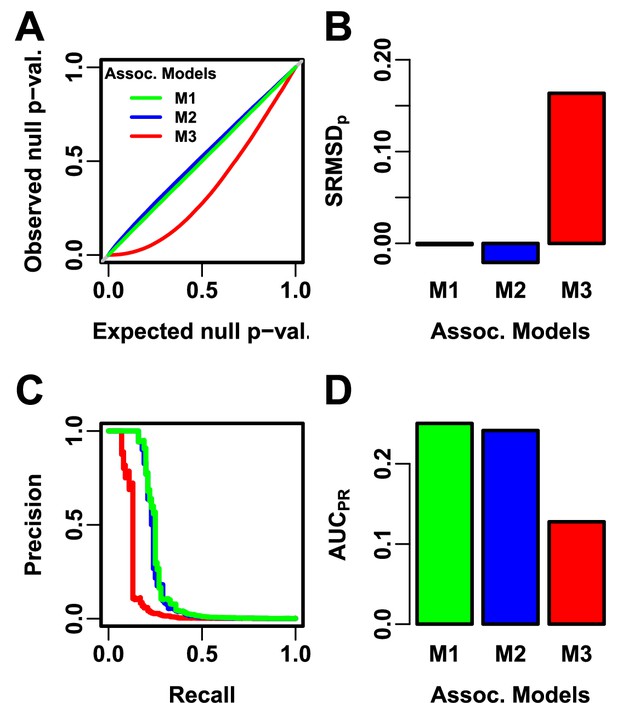
Illustration of evaluation measures.

Three archetypal models illustrate our complementary measures: M1 is ideal, M2 overfits slightly, M3 is naive. (A) QQ plot of p-values of “null” (non-causal) loci. M1 has desired uniform p-values, M2/M3 are miscalibrated. (B) ${SRMSD}_{p}$ (p-value Signed Root Mean Square Deviation) measures signed distance between observed and expected null p-values (closer to zero is better). (C) Precision and Recall (PR) measure causal locus classification performance (higher is better). (D) ${AUC}_{PR}$ (Area Under the PR Curve) reflects power (higher is better).

Figure 2—figure supplement 1

Download asset Open asset

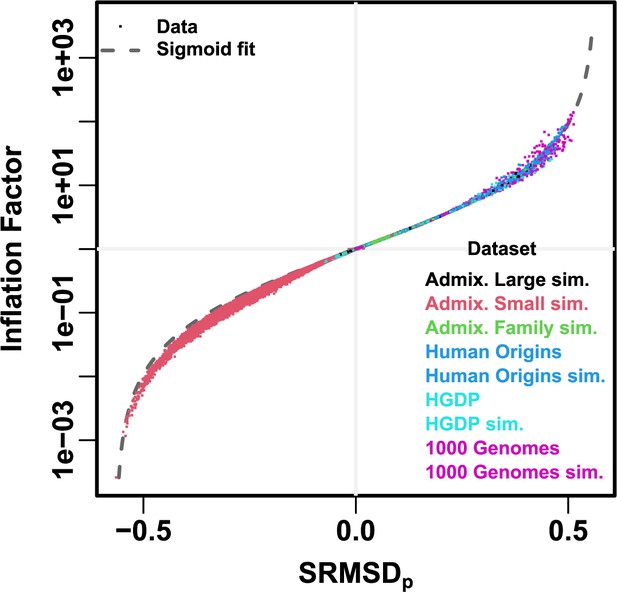
Comparison between ${SRMSD}_{p}$ and inflation factor.

Each point is a pair of statistics for one replicate, one association model (PCA or LMM with some number of PCs $r$ ), one trait model (FES vs RC, all heritability/environments tested), and one dataset (color coded by dataset). Note log y-axis. The sigmoidal curve in Equation 10 is fit to the data.

Figure 2—figure supplement 2

Download asset Open asset

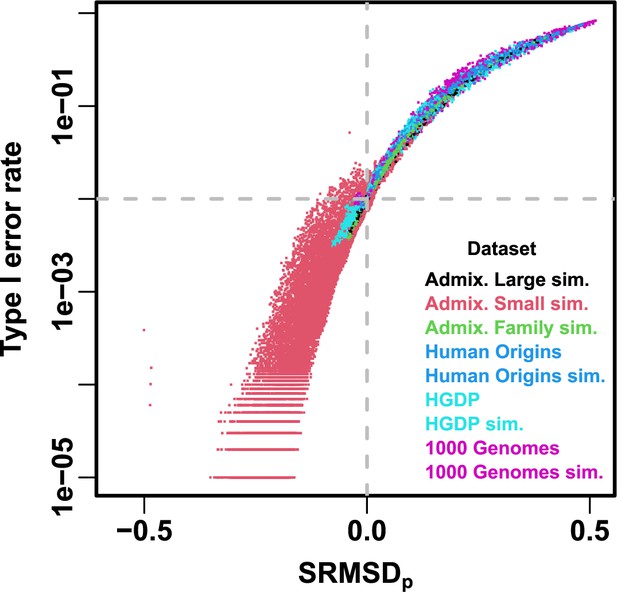
Comparison between ${SRMSD}_{p}$ and type I error rate.

Type I error rate calculated at a p-value threshold of 1e-2 (horizontal dashed gray line). Thus, a calibrated model has a type I error rate of 1e-2 and ${SRMSD}_{p} = 0$ (where the dashed lines meet). As expected, increased type I error rates correspond to ${SRMSD}_{p} > 0$ , while reduced type I error rates correspond to ${SRMSD}_{p} < 0$ . Each point is a pair of statistics for one replicate, one association model (PCA or LMM with some number of PCs $r$ ), one trait model (FES vs RC, all heritability/environments tested), and one dataset (color coded by dataset). Note log y-axis.

Figure 2—figure supplement 3

Download asset Open asset

Comparison between ${AUC}_{PR}$ and calibrated power.

Calibrated power is power calculated at an empirical type I error threshold of 1e-4. Each point is a pair of statistics for one replicate, one association model (PCA or LMM with some number of PCs $r$ ), one trait model (FES vs RC, all heritability/environments tested), and one dataset (color coded by dataset). Gray dashed line is $y = x$ line.

Figure 3 with 5 supplements

Download asset Open asset

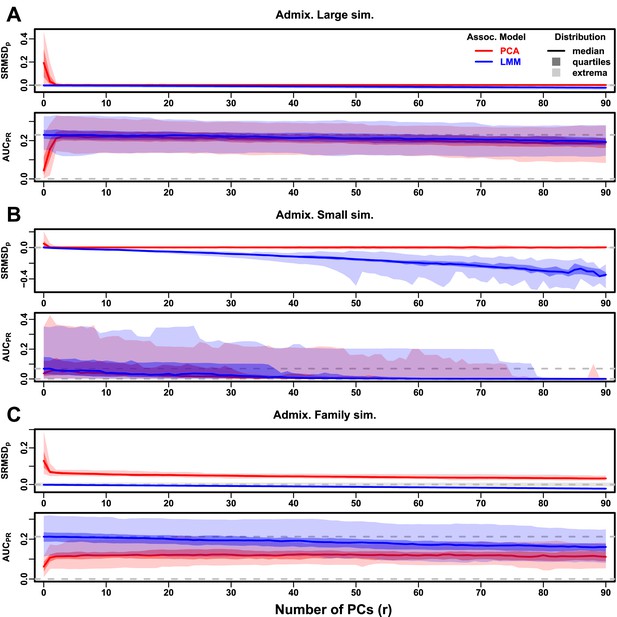
Evaluations in admixture simulations with FES traits, high heritability.

PCA and LMM models have varying number of PCs ( $r \in {0, \dots, 90}$ on x-axis), with the distributions (y-axis) of ${SRMSD}_{p}$ (top subpanel) and ${AUC}_{PR}$ (bottom subpanel) for 50 replicates. Best performance is zero ${SRMSD}_{p}$ and large ${AUC}_{PR}$ . Zero and maximum median ${AUC}_{PR}$ values are marked with horizontal gray dashed lines, and $| {SRMSD}_{p} | < 0.01$ is marked with a light gray area. LMM performs best with $r = 0$ , PCA with various $r$ . (A) Large simulation ( $n = 1, 000$ individuals). (B) Small simulation ( $n = 100$ ) shows overfitting for large $r$ . (C) Family simulation ( $n = 1, 000$ ) has admixed founders and large numbers of close relatives from a realistic random 20-generation pedigree. PCA performs poorly compared to LMM: ${SRMSD}_{p} > 0$ for all $r$ and large ${AUC}_{PR}$ gap.

Figure 3—figure supplement 1

Download asset Open asset

Evaluations in admixture simulations with RC traits, high heritability.

Figure 3—figure supplement 2

Download asset Open asset

Evaluations in admixture simulations with FES traits, low heritability.

Figure 3—figure supplement 3

Download asset Open asset

Evaluations in admixture simulations with RC traits, low heritability.

Figure 3—figure supplement 4

Download asset Open asset

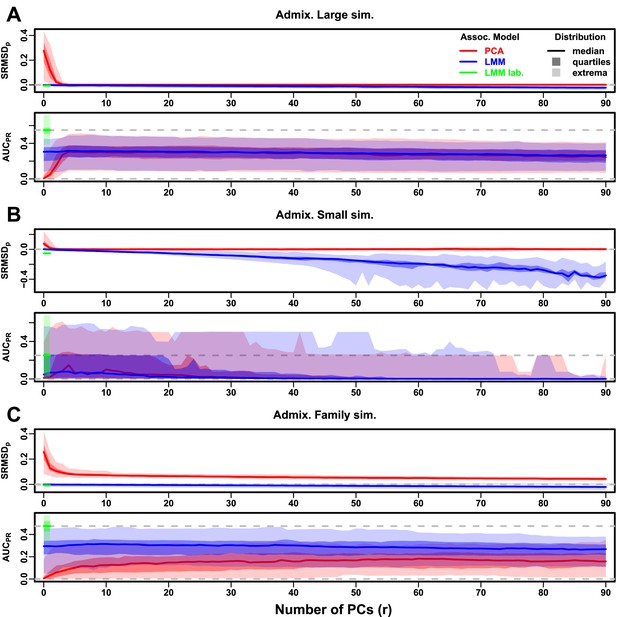
Evaluations in admixture simulations with FES traits, environment.

‘LMM lab.’ was only tested with $r = 0$ .

Figure 3—figure supplement 5

Download asset Open asset

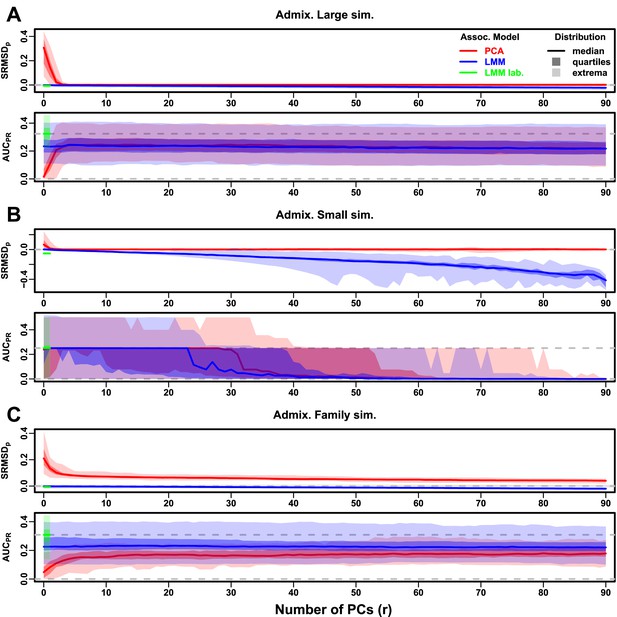
Evaluations in admixture simulations with RC traits, environment.

‘LMM lab.’ was only tested with $r = 0$ .

Figure 4 with 5 supplements

Download asset Open asset

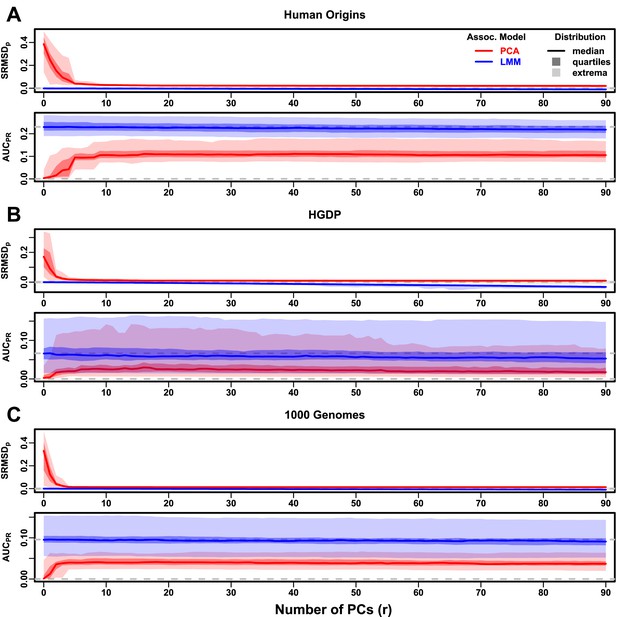
Evaluations in real human genotype datasets with FES traits, high heritability.

Same setup as Figure 3, see that for details. These datasets strongly favor LMM with no PCs over PCA, with distributions that most resemble the family simulation. (A) Human Origins. (B) Human Genome Diversity Panel (HGDP). (C) 1000 Genomes Project.

Figure 4—figure supplement 1

Download asset Open asset

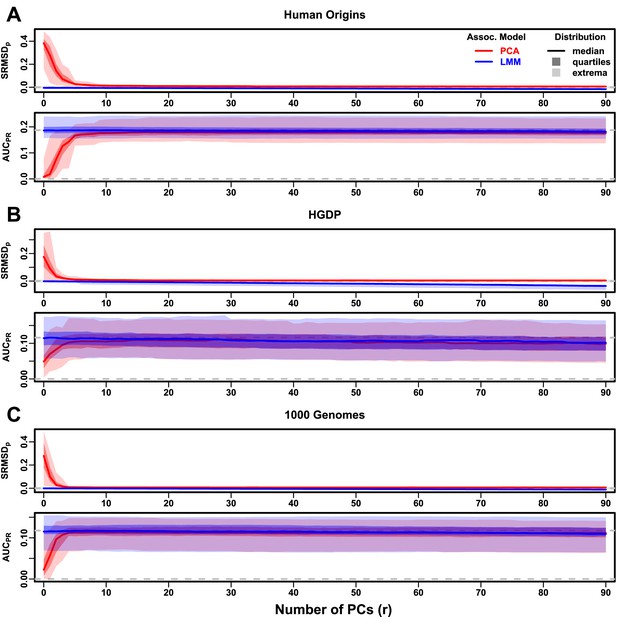
Evaluations in real human genotype datasets with RC traits, high heritability.

Figure 4—figure supplement 2

Download asset Open asset

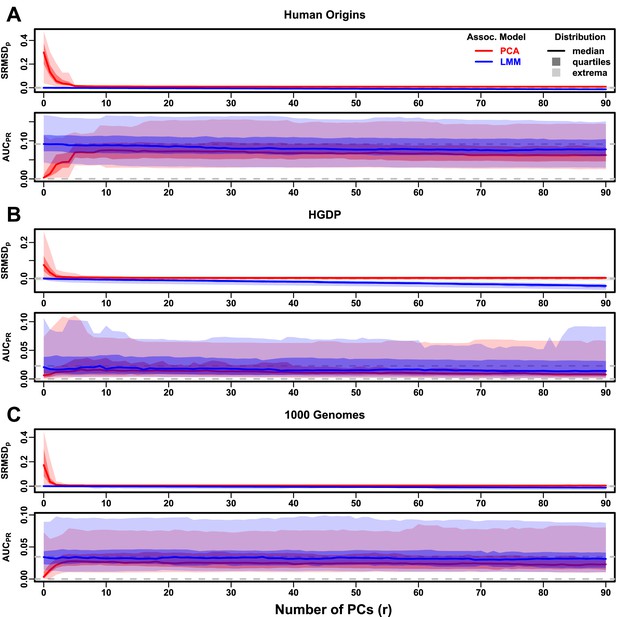
Evaluations in real human genotype datasets with FES traits, low heritability.

Figure 4—figure supplement 3

Download asset Open asset

Evaluations in real human genotype datasets with RC traits, low heritability.

Figure 4—figure supplement 4

Download asset Open asset

Evaluations in real human genotype datasets with FES traits, environment.

‘LMM lab.’ was only tested with $r = 0$ .

Figure 4—figure supplement 5

Download asset Open asset

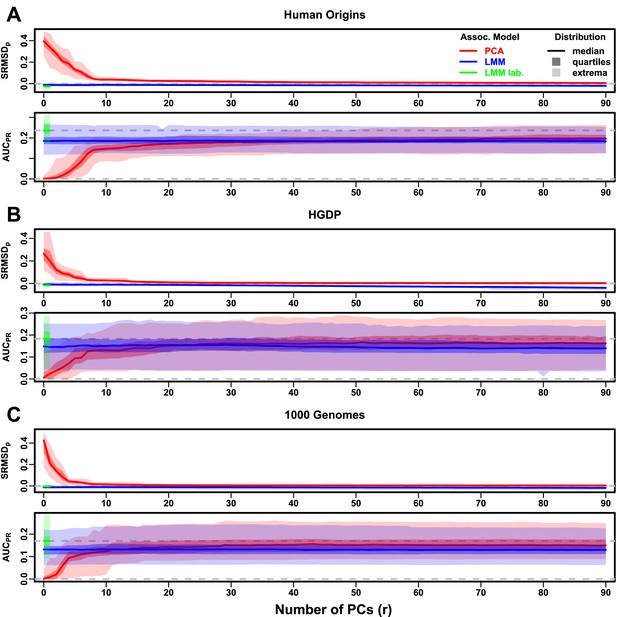
Evaluations in real human genotype datasets with RC traits, environment.

‘LMM lab.’ was only tested with $r = 0$ .

Figure 5 with 1 supplement

Download asset Open asset

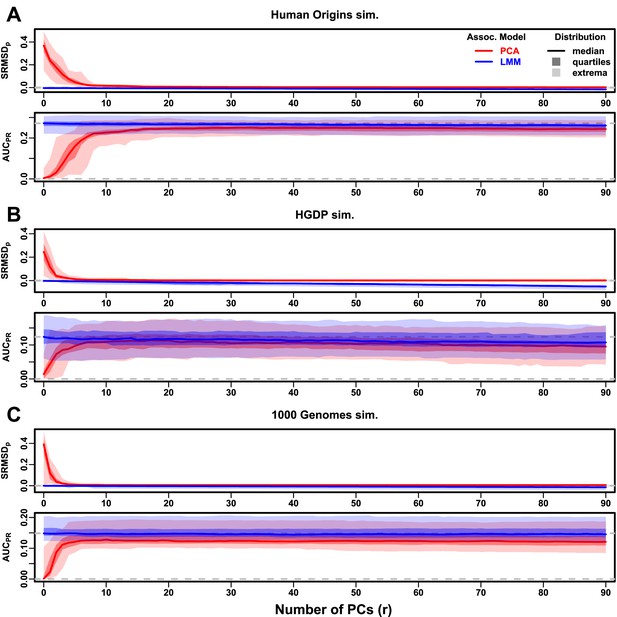
Evaluations in subpopulation tree simulations fit to human data with FES traits, high heritability.

Same setup as Figure 3, see that for details. These tree simulations, which exclude family structure by design, do not explain the large gaps in LMM-PCA performance observed in the real data. (A) Human Origins tree simulation. (B) Human Genome Diversity Panel (HGDP) tree simulation. (C) 1000 Genomes Project tree simulation.

Figure 5—figure supplement 1

Download asset Open asset

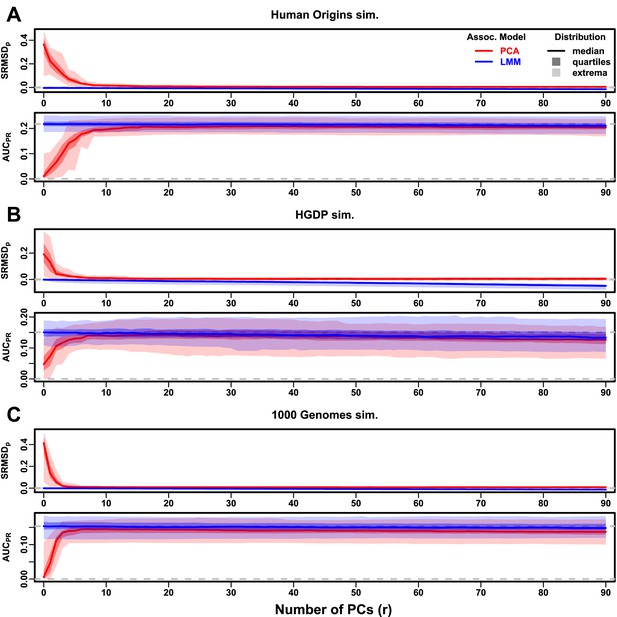
Evaluations in subpopulation tree simulations fit to human data with RC traits, high heritability.

Figure 6 with 2 supplements

Download asset Open asset

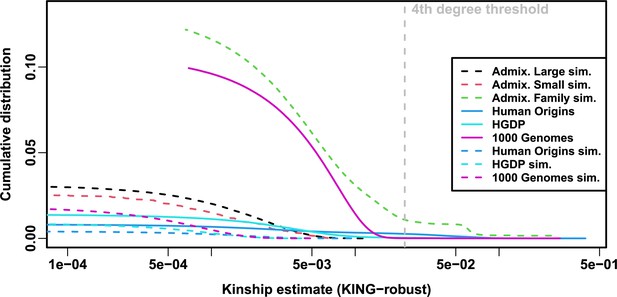
Local kinship distributions.

Curves are complementary cumulative distribution of lower triangular kinship matrix (self kinship excluded) from KING-robust estimator. Note log x-axis; negative estimates are counted but not shown. Most values are below 4th degree relative threshold. Each real dataset has a greater cumulative than its subpopulation tree simulations.

Figure 6—figure supplement 1

Download asset Open asset

Estimated relatedness dimensions of datasets.

(A) Kinship matrix rank estimated with the Tracy-Widom test with $p < 0.01$ . (B) Cumulative variance explained versus eigenvalue rank fraction. (C) Variance explained by first 10 eigenvalues.

Figure 6—figure supplement 2

Download asset Open asset

Number of PCs significantly associated with traits.

PCs are tested using an ordinary linear regression sequentially, with the th PC tested conditionally on the previous $k - 1$ PCs and the intercept. Q-values are estimated from the 90 p-values (one for each PC in a given dataset and replicate) using the R package qvalue assuming $π_{0} = 1$ (necessary since the default $π_{0}$ estimates were unreliable for such small numbers of p-values and occasionally produced errors), and an FDR threshold of 0.05 is used to determine the number of significant PCs. Distribution per dataset is over its 50 replicates. Shown are results for FES traits with $h^{2} = 0.8$ (the results for RC were very similar, not shown).

Figure 7 with 1 supplement

Download asset Open asset

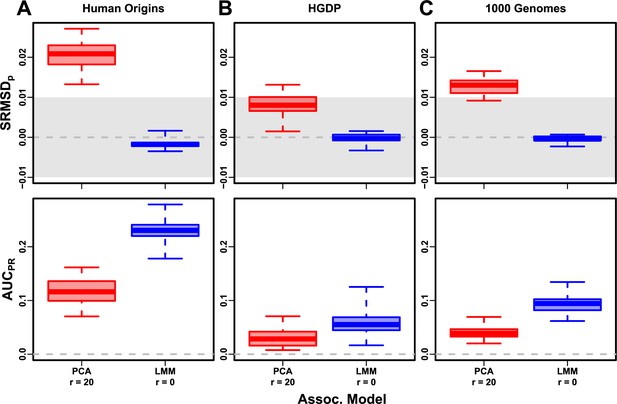
Evaluation in real datasets excluding 4th degree relatives, FES traits, high heritability.

Each dataset is a column, rows are measures. Boxplot whiskers are extrema over 50 replicates. First row has $| {SRMSD}_{p} | < 0.01$ band marked as gray area.

Figure 7—figure supplement 1

Download asset Open asset

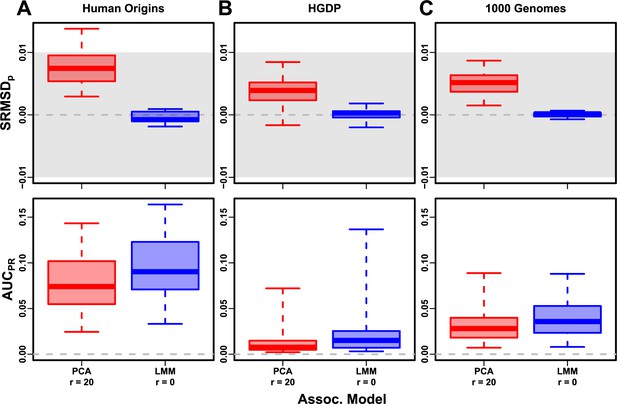
Evaluation in real datasets excluding 4th degree relatives, FES traits, low heritability.

Figure 8 with 1 supplement

Download asset Open asset

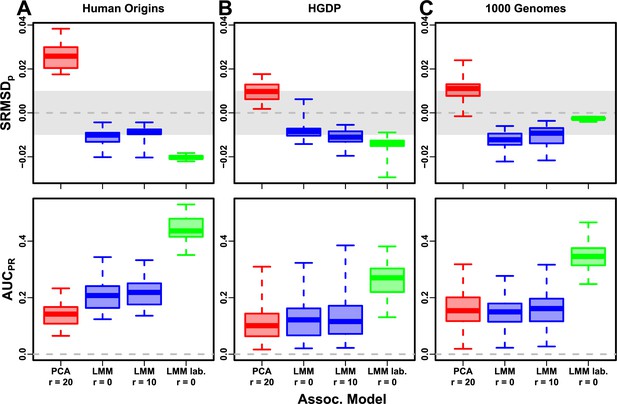
Evaluation in real datasets excluding 4th degree relatives, FES traits, environment.

Traits simulated with environment effects, otherwise the same as Figure 7. ‘LMM lab.’ includes as fixed effects true groups from which environment was simulated.

Figure 8—figure supplement 1

Download asset Open asset

Comparison of performance in low heritability vs environment simulations.

Each curve traces as the number of PCs $r$ is increased from $r = 0$ (marked with an “x”) until $r = 90$ (unmarked end), on one axis is the mean value over replicates of either ${SRMSD}_{p}$ or ${AUC}_{PR}$ , for low heritability simulations on the x-axis and environment simulations on the y-axis. Each curve corresponds to one dataset (color) and association model (solid or dashed line type). Columns: (A) FES and (B) RC traits show similar results. First row shows that for PCA curves (dashed), ${SRMSD}_{p}$ is higher (worse) in environment simulations for low $r$ , but becomes equal in both simulations once $r$ is sufficiently large; for LMM curves (solid), ${SRMSD}_{p}$ is equal in both simulations for all $r$ , all datasets. Second row shows that for PCA, ${AUC}_{PR}$ is higher (better) in low heritability simulations for low $r$ , but becomes higher in environment simulations once $r$ is sufficiently large; for LMM, performance is better in environment simulations for all $r$ , all datasets.

Tables

Table 1

Previous PCA-LMM evaluations in the literature.

	Sim. Genotypes			General
Publication	Type*	$K$ ^†	$F_{ST}$ ^‡	Real ^§	Trait ^¶	Power	$P C s (r)$	Best
Zhao et al., 2007				✓	Q	✓	8	LMM
Zhu and Yu, 2009	I, A, F	3, 8	≤0.15	✓	Q	✓	1–22	LMM
Astle and Balding, 2009	I	3	0.10		CC	✓	10	Tie
Kang et al., 2010				✓	Both		2–100	LMM
Price et al., 2010	I, F	2	0.01		CC		1	Mixed
Wu et al., 2011	I, A	2–4	0.01		CC	✓	10	Mixed
Liu et al., 2011	S, A	2–3	R		Q	✓	10	Tie
Sul and Eskin, 2013	I	2	0.01		CC		1	Tie
Tucker et al., 2014	I	2	0.05	✓	Both	✓	5	Tie
Yang et al., 2014				✓	CC	✓	5	Tie
Song et al., 2015	S, A	2–3	R		Q		3	LMM
Loh et al., 2015				✓	Q	✓	10	LMM
Zhang and Pan, 2015				✓	Q	✓	20–100	LMM
Liu et al., 2016				✓	Q	✓	3–6	LMM
Sul et al., 2018				✓	Q		100	LMM
Loh et al., 2018				✓	Both	✓	20	LMM
Mbatchou et al., 2021				✓	Both		1	LMM
This work	A, T, F	10–243	≤0.25	✓	Q	✓	0–90	LMM

*

Genotype simulation types. I: Independent subpopulations; S: subpopulations (with parameters drawn from real data); A: Admixture; T: Subpopulation Tree; F: Family.
†

Model dimension (number of subpopulations or ancestries).
‡

R: simulated parameters based on real data, $F_{ST}$ not reported.
§

Evaluations using unmodified real genotypes.
¶

Q: quantitative; CC: case-control.

Table 2

Features of simulated and real human genotype datasets.

Dataset	Type	$L o c i (m)$	Ind. ( $n$ )	Subpops.* ( $K$ )	Causal loci^† ( $m_{1}$ )	$F_{ST}$ ^‡
Admix. Large sim.	Admix.	100 000	1000	10	100	0.1
Admix. Small sim.	Admix.	100 000	100	10	10	0.1
Admix. Family sim.	Admix.+Pedig.	100 000	1000	10	100	0.1
Human Origins	Real	190 394	2922	11–243	292	0.28
HGDP	Real	771 322	929	7–54	93	0.28
1000 Genomes	Real	1 111 266	2504	5–26	250	0.22
Human Origins sim.	Tree	190 394	2922	243	292	0.23
HGDP sim.	Tree	771 322	929	54	93	0.25
1000 Genomes sim.	Tree	1 111 266	2504	26	250	0.21

*

For admixed family, ignores additional model dimension of 20 generation pedigree structure. For real datasets, lower range is continental subpopulations, upper range is number of fine-grained subpopulations.
†

$m_{1} = round (n h^{2} / 8)$ to balance power across datasets, shown for $h^{2} = 0.8$ only.
‡

Model parameter for simulations, estimated value on real datasets.

Table 3

Overview of PCA and LMM evaluations for high heritability simulations.

			LMM $r = 0$ vs best $r$			PCA vs LMM $r = 0$
Dataset	Metric	Trait*	Cal.^†	Best $r$ ^‡	P-value ^§	Best $r$ ^‡	Cal.^†	P-value ^§	Best model ^¶
Admix. Large sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	12	True	0.036	Tie
Admix. Small sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	4	True	0.055	Tie
Admix. Family sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	90	False	3.9e-10*	LMM
Human Origins	$\| {SRMSD}_{p} \|$	FES	True	0	1	89	False	3.9e-10*	LMM
HGDP	$\| {SRMSD}_{p} \|$	FES	True	0	1	87	True	4.4e-10*	LMM
1000 Genomes	$\| {SRMSD}_{p} \|$	FES	True	0	1	90	False	3.9e-10*	LMM
Human Origins sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	88	True	0.017	Tie
HGDP sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	47	True	0.046	Tie
1000 Genomes sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	78	True	9.6e-10*	LMM
Admix. Large sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	26	True	0.11	Tie
Admix. Small sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	4	True	0.00097	Tie
Admix. Family sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	90	False	3.9e-10*	LMM
Human Origins	$\| {SRMSD}_{p} \|$	RC	True	0	1	90	True	0.00065	Tie
HGDP	$\| {SRMSD}_{p} \|$	RC	True	0	1	37	True	1.5e-05*	LMM
1000 Genomes	$\| {SRMSD}_{p} \|$	RC	True	0	1	76	True	3.9e-10*	LMM
Human Origins sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	85	True	0.14	Tie
HGDP sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	44	True	8.8e-07*	LMM
1000 Genomes sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	90	True	3.9e-10*	LMM
Admix. Large sim.	${AUC}_{PR}$	FES		0	1	3		5.9e-06*	LMM
Admix. Small sim.	${AUC}_{PR}$	FES		0	1	2		0.025	Tie
Admix. Family sim.	${AUC}_{PR}$	FES		1	0.35	22		3.9e-10*	LMM
Human Origins	${AUC}_{PR}$	FES		0	1	34		3.9e-10*	LMM
HGDP	${AUC}_{PR}$	FES		1	0.33	16		4.4e-10*	LMM
1000 Genomes	${AUC}_{PR}$	FES		1	0.11	8		3.9e-10*	LMM
Human Origins sim.	${AUC}_{PR}$	FES		0	1	36		3.9e-10*	LMM
HGDP sim.	${AUC}_{PR}$	FES		0	1	17		1.7e-05*	LMM
1000 Genomes sim.	${AUC}_{PR}$	FES		0	1	10		5e-10*	LMM
Admix. Large sim.	${AUC}_{PR}$	RC		0	1	3		1.4e-05*	LMM
Admix. Small sim.	${AUC}_{PR}$	RC		0	1	1		0.095	Tie
Admix. Family sim.	${AUC}_{PR}$	RC		0	1	34		3.9e-10*	LMM
Human Origins	${AUC}_{PR}$	RC		3	0.4	36		9.6e-10*	LMM
HGDP	${AUC}_{PR}$	RC		4	0.21	16		0.013	Tie
1000 Genomes	${AUC}_{PR}$	RC		5	0.004	9		0.00043	Tie
Human Origins sim.	${AUC}_{PR}$	RC		0	1	37		4.1e-10*	LMM
HGDP sim.	${AUC}_{PR}$	RC		3	0.087	17		0.0014	Tie
1000 Genomes sim.	${AUC}_{PR}$	RC		3	0.37	10		8.5e-10*	LMM

*

FES: Fixed Effect Sizes, RC: Random Coefficients.
†

Calibrated: whether mean $| {SRMSD}_{p} | < 0.01$ over 50 replicates.
‡

Value of $r$ (number of PCs) with minimum mean $| {SRMSD}_{p} |$ or maximum mean ${AUC}_{PR}$ .
§

Wilcoxon paired 1-tailed test of distributions ( $| {SRMSD}_{p} |$ or ${AUC}_{PR}$ ) between models in header. Asterisk marks significant value using Bonferroni threshold ( $p < α / n_{tests}$ with $α = 0.01$ and $n_{tests} = 72$ is the number of tests in this table).
¶

Tie if no significant difference using Bonferroni threshold.

Table 4

Dataset sizes after 4th degree relative filter.

Dataset	Loci ( $m$ )	Ind. ( $n$ )	Ind. removed (%)
Human Origins	189 722	2636	9.8
HGDP	758 009	847	8.8
1000 Genomes	1 097 415	2390	4.6

Table 5

Overview of PCA and LMM evaluations for low heritability simulations.

			LMM $r = 0$ vs best $r$			PCA vs LMM $r = 0$
Dataset	Metric	Trait*	Cal.^†	Best $r$ ^‡	p-value ^§	Best $r$ ^‡	Cal.^†	p-value ^§	Best model ^¶
Admix. Large sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	62	True	0.00012*	LMM
Admix. Small sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	3	True	0.27	Tie
Admix. Family sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	90	False	3.9e-10*	LMM
Human Origins	$\| {SRMSD}_{p} \|$	FES	True	0	1	81	True	3.9e-10*	LMM
HGDP	$\| {SRMSD}_{p} \|$	FES	True	0	1	37	True	6.2e-09*	LMM
1000 Genomes	$\| {SRMSD}_{p} \|$	FES	True	0	1	84	True	3.9e-10*	LMM
Admix. Large sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	35	True	0.00094	Tie
Admix. Small sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	3	True	0.087	Tie
Admix. Family sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	90	False	4.1e-10*	LMM
Human Origins	$\| {SRMSD}_{p} \|$	RC	True	0	1	75	True	0.00016*	LMM
HGDP	$\| {SRMSD}_{p} \|$	RC	True	0	1	23	True	1.7e-05*	LMM
1000 Genomes	$\| {SRMSD}_{p} \|$	RC	True	0	1	41	True	6.7e-10*	LMM
Admix. Large sim.	${AUC}_{PR}$	FES		0	1	3		0.11	Tie
Admix. Small sim.	${AUC}_{PR}$	FES		0	1	0		0.58	Tie
Admix. Family sim.	${AUC}_{PR}$	FES		0	1	7		2.2e-06*	LMM
Human Origins	${AUC}_{PR}$	FES		0	1	16		8e-10*	LMM
HGDP	${AUC}_{PR}$	FES		11	0.68	6		0.0043	Tie
1000 Genomes	${AUC}_{PR}$	FES		6	0.34	4		2.3e-07*	LMM
Admix. Large sim.	${AUC}_{PR}$	RC		0	1	3		0.14	Tie
Admix. Small sim.	${AUC}_{PR}$	RC		0	1	0		0.1	Tie
Admix. Family sim.	${AUC}_{PR}$	RC		0	1	5		1.9e-06*	LMM
Human Origins	${AUC}_{PR}$	RC		4	0.16	12		0.003	Tie
HGDP	${AUC}_{PR}$	RC		2	0.14	5		0.14	Tie
1000 Genomes	${AUC}_{PR}$	RC		0	1	4		0.078	Tie

*

FES: Fixed Effect Sizes, RC: Random Coefficients.
†

Calibrated: whether mean $| {SRMSD}_{p} | < 0.01$ over 50 replicates.
‡

Value of $r$ (number of PCs) with minimum mean $| {SRMSD}_{p} |$ or maximum mean ${AUC}_{PR}$ .
§

Wilcoxon paired 1-tailed test of distributions ( $| {SRMSD}_{p} |$ or ${AUC}_{PR}$ ) between models in header. Asterisk marks significant value using Bonferroni threshold ( $p < α / n_{tests}$ with $α = 0.01$ and $n_{tests} = 48$ is the number of tests in this table).
¶

Tie if no significant difference using Bonferroni threshold.

Table 6

Overview of PCA and LMM evaluations for environment simulations.

			LMM $r = 0$ vs best $r$			PCA vs LMM $r = 0$				LMM lab. $r = 0$ vs PCA/LMM
Dataset	Metric	Trait*	Cal.^†	$r$ ^‡	p-value ^§	$r$ ^‡	Cal.^†	p-value ^§	Best ^¶	Cal.^†	p-value ^§	Best ^¶
Admix. Large sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	83	True	0.38	Tie	True	1.8e-14*	PCA/LMM
Admix. Small sim.	$\| {SRMSD}_{p} \|$	FES	True	0	1	90	True	0.001	Tie	False	1.4e-14*	PCA/LMM
Admix. Family sim.	$\| {SRMSD}_{p} \|$	FES	True	4	0.18	90	False	3.9e-10*	LMM	True	0.066	LMM/LMM lab.
Human Origins	$\| {SRMSD}_{p} \|$	FES	True	9	3.9e-05*	90	False	1.4e-08*	LMM	False	3.9e-10*	LMM
HGDP	$\| {SRMSD}_{p} \|$	FES	True	0	1	90	True	0.0037	Tie	False	2.1e-09*	PCA/LMM
1000 Genomes	$\| {SRMSD}_{p} \|$	FES	False	8	8.8e-08*	85	True	0.053	Tie	True	3.9e-10*	LMM lab.
Admix. Large sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	60	True	0.033	Tie	True	6.3e-10*	PCA/LMM
Admix. Small sim.	$\| {SRMSD}_{p} \|$	RC	True	0	1	9	True	0.85	Tie	False	1.4e-14*	PCA/LMM
Admix. Family sim.	$\| {SRMSD}_{p} \|$	RC	True	5	0.14	90	False	3.9e-10*	LMM	True	0.011	LMM/LMM lab.
Human Origins	$\| {SRMSD}_{p} \|$	RC	False	9	1.1e-08*	90	True	2.3e-07*	PCA	False	3.9e-10*	PCA
HGDP	$\| {SRMSD}_{p} \|$	RC	True	0	1	89	True	6.5e-09*	PCA	False	3.9e-10*	PCA
1000 Genomes	$\| {SRMSD}_{p} \|$	RC	False	8	1.6e-08*	88	True	4.9e-09*	PCA	True	0.09	PCA/LMM lab.
Admix. Large sim.	${AUC}_{PR}$	FES		4	2.4e-06*	6		0.0021	Tie		1.8e-15*	LMM lab.
Admix. Small sim.	${AUC}_{PR}$	FES		3	0.055	4		0.033	Tie		0.28	Tie
Admix. Family sim.	${AUC}_{PR}$	FES		12	7e-04	63		3.9e-10*	LMM		3.9e-10*	LMM lab.
Human Origins	${AUC}_{PR}$	FES		20	3.7e-06*	90		1.4e-05*	LMM		3.9e-10*	LMM lab.
HGDP	${AUC}_{PR}$	FES		12	4.3e-06*	45		0.0044	Tie		3.9e-10*	LMM lab.
1000 Genomes	${AUC}_{PR}$	FES		9	1.9e-08*	55		0.028	Tie		3.9e-10*	LMM lab.
Admix. Large sim.	${AUC}_{PR}$	RC		4	0.00085	5		0.0018	Tie		5e-10*	LMM lab.
Admix. Small sim.	${AUC}_{PR}$	RC		2	0.13	5		0.093	Tie		0.0028	Tie
Admix. Family sim.	${AUC}_{PR}$	RC		9	0.01	86		1.7e-09*	LMM		3.9e-10*	LMM lab.
Human Origins	${AUC}_{PR}$	RC		22	0.0039	90		1e-06*	PCA		3.9e-10*	LMM lab.
HGDP	${AUC}_{PR}$	RC		19	0.0057	64		2.8e-05*	PCA		3e-07*	LMM lab.
1000 Genomes	${AUC}_{PR}$	RC		9	8.7e-05*	87		1.2e-09*	PCA		4.4e-10*	LMM lab.

*

FES: Fixed Effect Sizes, RC: Random Coefficients.
†

Calibrated: whether mean $| {SRMSD}_{p} | < 0.01$ over 50 replicates.
‡

Value of $r$ (number of PCs) with minimum mean $| {SRMSD}_{p} |$ or maximum mean ${AUC}_{PR}$ .
§

Wilcoxon paired 1-tailed test of distributions ( $| {SRMSD}_{p} |$ or ${AUC}_{PR}$ ) between models in header. Asterisk marks significant value using Bonferroni threshold ( $p < α / n_{tests}$ with $α = 0.01$ and $n_{tests} = 72$ is the number of tests in this table).
¶

Tie if no significant difference using Bonferroni threshold; in last column, pairwise ties are specified and “Tie” is three-way tie.